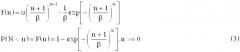Способ прогноза штормовых подъемов уровня воды

Способ прогноза штормовых подъемов уровня воды

Иллюстрации

Показать все

Реферат

Предлагаемое техническое решение относится к области гидрометеорологии, в частности к технологиям прогнозирования штормовых подъемов уровней воды (наводнений).

Известен способ подъема уровня воды, основанный на формуле Н.И. Бельского (Бельский Н.И. Синоптические условия Ленинградских наводнений. - «Тр. ГОИН», 1954. Вып. 27(39). С. 43-80 [1]). Способ относится к эмпирическим и применялся в оперативной практике в Северо-Западном регионе, в частности для прогноза штормовых подъемов уровней воды для устьевых участков рек Балтийского бассейна.

Способ основывается на использовании синоптической информации, а также учете региональных физико-географических условий. Основной идеей, заложенной в способе, является учет взаимодействия метеорологических и гидрологических факторов и их роль в процессе наводнения; типов колебаний уровня воды в море, в частности Балтийском море и Финском заливе; возникновения, перемещения и трансформации длинной волны, влияния метеорологических условий над Финским заливом на степень возрастания высоты длинной волны.

Применение данного способа достаточно просто и удобно, однако он имеет существенные недостатки.

Одним из главных недостатков является ограниченная заблаговременность прогноза от 3 до 6 часов. Кроме того, эмпирические коэффициенты в прогностических формулах отражают лишь те синоптические условия, для которых они получены, их применение для ситуаций экстремальных атмосферных процессов очень ограничены.

Известен также способ прогноза штормовых подъемов уровня воды при помощи гидродинамической модели Балтийского моря типа BSM (К.А. Клеванный. Наводнения в Санкт-Петербурге при незавершенном комплексе защитных сооружений // Изв. АН. Серия географическая, 2002, 2, с. 80-88 [2]).

Модель BSM представляет собой замкнутую систему уравнений мелкой воды и двумерное уравнение переноса примесей в криволинейных координатах. Модель предполагает расчет длинноволновых процессов и переноса примесей в произвольной акватории на основе метода криволинейных координат. Уравнения модели решаются полунеявным конечно-разностным методом. Используется C-сетка Мезингера-Аракавы, центрально-разностная аппроксимация пространственных производных и аппроксимация Кранка-Николсона по времени. Расчетным блоком модели управляет пакет программ на базе системы CARDINAL.

Способ реализован в системе прогноза наводнений в реке Нева. Реализовано объединение гидродинамической системы с региональной атмосферной моделью, которая, в свою очередь, соединена с глобальной атмосферной моделью. Такие модели, по сути, являются вложенными и позволяют с большей точностью задавать начальные и граничные условия. Временной шаг модели составляет 180 с, пространственный шаг переменный по акватории Балтийского моря и изменяется от 16 м в Невской губе до 1000 м на акватории Балтики.

Наиболее важным требованием, обеспечивающим качество гидродинамических прогнозов, является точность и подробность (шаг сетки) задания исходной информации. В первую очередь это относится к прогнозу скорости приводного ветра и его изменчивости, зависящих от прохождения фронтальных разделов, эволюции циклонических образований, взрывного циклогенеза и соответственно активного развития штормовых циклонов. Другими важными факторами формирования нагонов являются направление ветра и продолжительность действия эффективного (т.е. наиболее благоприятного по направлению для формирования нагона) ветра.

Недостатком способа является необходимость использования в модели большого объема разнообразной информации, подготовка которой требует довольно много времени ввиду очень высокой сложности явления. Заблаговременность прогноза невелика, уверенный прогноз не превышает 6 часов.

Кроме того, способ не учитывает факторы, связанные с особенностями развития штормовых циклонов, включая взрывной циклогенез, активизацию фронтальных разделов, в том числе прохождение вторичных холодных фронтов, формирование шквалистого усиления ветра.

Не учитывается влияние орографии, а также усиление ветра при порывах, так как возможность возникновения значительного нагона определяется структурой приземного атмосферного давления, при численной аппроксимации оно принимается постоянным в пространстве в области расчета (шаг сети точек), а направление и скорость ветра - однородными в пределах отдельных районов.

Известен также способ прогноза штормовых подъемов уровней воды для морских устьевых участков рек (патент RU №2521216 C2, 27.06.2014 [3]), задачей которого является повышение заблаговременности прогноза подъема уровней воды до 72 часов по сравнению с аналогами (максимальная надежная заблаговременность). При этом техническим результатом изобретения является разделение года на два периода: «наводненческий период» и «ненаводненческий период», что позволяет выявить функциональные зависимости между особенностями крупномасштабных атмосферных процессов и штормовыми подъемами уровней воды в морских устьевых участках рек, а также сократить период активного прогнозирования; разработка универсального способа качественного прогноза штормовых подъемов уровней воды для морских устьевых участков рек с максимальной заблаговременностью.

Для реализации способа необходимо сформировать архив данных об экстремальных подъемах уровней воды (наводнениях), включающий в себя соответствующие даты и уровни воды, по посту, имеющему максимально длинный период наблюдений на соответствующем морском устьевом участке реки.

Под наводнением в данном случае понимается количественная характеристика подъема уровня воды на морском устьевом участке реки более 150 см.

Первоначально группируются наводнения из архива по месяцам года за весь период наблюдений. После чего определяется количество наводнений для каждого месяца.

Рассчитывается повторяемость наводнений для каждого месяцам за весь период наблюдений. Для этого ранее определенное количество наводнений в месяце делят на общее число наблюдений.

Далее осуществляется последовательное исключение месяцев за весь период наблюдений, при которых повторяемость наводнения ниже 1%. Таким образом, из оставшихся месяцев формируется «наводненческий период», т.е. под «наводненческим периодом» года понимаются те месяцы года, в которые повторяемость наводнения выше 1%.

Для «наводненческого» периода формируем архив полей приземного атмосферного давления по срочным данным (за два срока) для территории формирования штормовых циклонов над рассматриваемым морским устьевым участком реки за весь период наблюдений.

Реализуемый подход, основанный на анализе всех полей приземного атмосферного давления, связанных с формированием «наводненческих ситуаций», позволяет учесть основные особенности, связанные с активным развитием штормовых циклонов, включая взрывной циклогенез, активизацию фронтальных разделов, в том числе прохождение вторичных холодных фронтов, формирование шквалистого усиления ветра.

Кроме того, использование поля приземного атмосферного давления позволяет учесть орографию региона через структуру атмосферных процессов, которая формируется непосредственно под влиянием физико-географических процессов.

Поле приземного атмосферного давления представляет собой распределение значений приземного атмосферного давления в узлах регулярной географической сетки (5°φ на 5°λ) с координатами (φ_i, λ_j) (i·j=n). Размер поля приземного атмосферного давления определяется размером формирования циклонов в районе морского устьевого участка реки, для которого дается прогноз.

Для каждого из месяцев «наводненческого периода» рассчитывают эмпирические ортогональные функции (ЭОФ) по полям приземного атмосферного давления за весь период наблюдений. Эмпирические ортогональные функции предназначены для сжатия информации при анализе крупных барических образований, когда физические процессы в поле метеорологического параметра можно достаточно полно описать статистическими особенностями первых трех коэффициентов, в которых сосредотачивается до 80-85% дисперсии данного элемента.

В основе расчета ЭОФ лежит разложение поля приземного атмосферного давления P(x_k) по новой системе координат:

P ( x k ) = ∑ α Ψ α k n α = 1 ,

где Ψα_k - новая ортогональная система координат, называемая эмпирическими ортогональными функциями;

а α - коэффициенты разложения барического поля P(x_k) по новой системе координат Ψα_k, называемые эмпирическими ортогональными составляющими (ЭОС).

ЭОФ представляют собой собственные векторы корреляционной матрицы поля давления, полученной по временному ряду наблюдения поля приземного атмосферного давления. Для получения корреляционных матриц и их собственных векторов используется стандартное программное обеспечение.

Для каждого срока по каждому месяцу «наводненческого периода» за весь период наблюдений по ЭОФ определяются ЭОС. Для обеспечения не менее 85% дисперсии количество ЭОС достаточно первых трех коэффициентов. Для дат наводнения по каждому месяцу выделяются первые три ЭОС, являющиеся базой для выявления «наводненческих ситуаций». Для каждого месяца «наводненческого периода» выделяем диапазон первых трех коэффициентов ЭОС (по минимальному и максимальному значению ЭОС). Ситуации, ЭОС которых попадают внутрь этогол диапазона, будем считать «наводненческими ситуациями».

Таким образом, сформирована эталонная область ЭОС, соответствующая наводнениям для каждого месяца «наводненческого» периода. Под наводненческой ситуацией понимается тип приземного поля атмосферного давления, при котором на рассматриваемой территории формируется наводнение.

Собственно способ прогноза штормовых подъемов уровней воды в морских устьевых участках рек заключается в определении наступления/ненаступления «наводненческой ситуации» с заблаговременностью от 6 до 72 часов.

Исходной информацией для прогноза подъемов уровней воды (наводнений) в морских устьевых участках рек служат фоновые прогностические поля приземного атмосферного давления за срок от 6 до 72 часов, представленные в виде, аналогичном архивным полям приземного атмосферного давления. Соответственно в каждой точке представлена величина приземного атмосферного давления, которая может быть получена путем численного прогноза с использованием гидродинамической модели атмосферы, имеющей наиболее высокий уровень оправдываемости в данном регионе. По прогностическому полю приземного атмосферного давления с заблаговременностью от 6 до 72 часов рассчитываются ЭОС по ЭОФ данного месяца, полученным по всему архиву полей и сопоставляются с эталонной областью ЭОС. По результатам сопоставления делается вывод о наступлении или ненаступлении на анализируемый прогностический срок «наводненческой ситуации», а следовательно, наводнения. Для месяцев, не вошедших в «наводненческий период», наводнения считаются маловероятным событием и не относятся к «наводненческим ситуациям», что позволяет также сократить период активного прогнозирования.

Использование известного способа [3] позволяет сократить период активного прогнозирования за счет исключения из анализа месяцы, не вошедшие в «наводненческий период», однако, расчет эмпирических ортогональных функции (ЭОФ) только по полям приземного атмосферного давления за весь период наблюдений для каждого из месяцев «наводненческого периода» не позволяет в полной мере оценить реальные пространственно-временные распределения гидрометеорологических условий, которые представляют собой сложную пятнистую структуру со свойствами динамического хаоса, которая носит название «перемежаемости». Пятна квазиоднородных значений гидрометеорологических характеристик имеют чрезвычайно нерегулярные (извилистые) геометрические очертания, различные площади. Единственной устойчивой их характеристикой является функция распределения числа пятен по площади. Она является степенным распределением - больших пятен мало (максимальное - одно), а малых много. Эта особенность пространственно-временного распределения гидрометеорологических характеристик снижает требования к гидрометеорологической информации, обеспечивающей принятие решений на обеспечение безопасности судовождения.

С другой стороны, при принятии решения эффективность решения задачи с учетом гидрометеоусловий определяется, в конечном счете, возможностью выполнения этой задачи в реальных погодных условиях. Задача решается, если существуют благоприятные условия среды на пространственно-временном интервале, необходимом для ее выполнения. Такое понимание возможности выполнения задачи требует достаточно детального описания пространственно-временной изменчивости геопространственных полей. В настоящее время для этой цели используют вероятностные (статистические) параметры, например, среднеквадратическое отклонение гидрометеорологических характеристик. Однако эти параметры не позволяют описать перемежаемость, так как это "интегральные" характеристики изменчивости, которые не характеризуют структуру пятнистости погодных условий.

Задачей предлагаемого технического решения является расширение функциональных возможностей способа прогноза штормовых подъемов уровней воды как для морских устьевых участков рек или наводнений, так и на морских акваториях.

Поставленная задача решается за счет того, что в способе прогноза штормовых подъемов уровней воды или наводнений, заключающемся в создании архива наводнений (дата-уровень) за максимально возможный период, подготовке архива полей приземного атмосферного давления по срочным данным (за два срока) в районе формирования штормовых циклонов, расчете повторяемости наводнений по всем месяцам года, выделение по величине повторяемости наводнений «наводненческий период» (повторяемость больше 1%) и «ненаводненческий период» года для месяцев, вошедших в «ненаводненческий период», наводнения считаются маловероятным событием и автоматически делается вывод о ненаступлении «наводненческой ситуации», определяются эмпирические ортогональные функции (ЭОФ) по всему архиву срочных наблюдений полей приземного атмосферного давления для каждого месяца «наводненческого периода», рассчитываются эмпирические ортогональные составляющие (ЭОС) для каждого месяца «наводненческого периода», выделяется диапазон трех первых ЭОС от минимального до максимального значения для дат наводнений каждого месяца «наводненческого периода», формируется эталонная область ЭОС для каждого месяца, по результатам оперативного гидродинамического прогноза поля приземного атмосферного давления рассчитываются ЭОС по ранее созданным ЭОФ для данного месяца, по которым определяется принадлежность ЭОС прогностического поля к эталонной области ЭОС наводнений прогнозируемого месяца, делается вывод о наступлении/ненаступлении на анализируемый прогностический срок «наводненческой ситуации», в котором при анализе прогностического срока «наводненческой ситуации» рассчитывают число штормов с непрерывной продолжительностью для доверительной вероятности штормовых условий, выявляют промежуток времени продолжительностью, в пределах которого скорость ветра позволяет выполнить, например, безопасный переход судна, определяют пространственное распределение фазы колебаний акватории по измерениям высоты уровня моря посредством альтиметрических спутников с выделением приливных и сейшевых колебаний уровня моря.

Сущность предлагаемого технического решения иллюстрируется чертежами (фиг. 1-8).

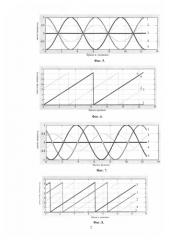
Фиг. 1. Результаты имитации штормов и окон погоды для повторяемости штормовых условий с доверительной вероятностью 12.5%.

Фиг. 2. Пример временного хода скорости ветра (а) и соответствующая ему временная развертка штормов и окон погоды (б).

Фиг. 3. Схема акватории с сейшевыми колебаниями.

Фиг. 4. Схема акватории с приливными колебаниями: радиальные прямые - изофазы, в центре акватории - амфидромическая точка (точка 3).

Фиг. 5. График временного хода сейшевых колебаний высоты уровня на акватории (фиг. 3, точки 1-5).

Фиг. 6. График временного хода сейшевых колебаний фаз уровня на акватории (фиг. 3, точки 1-5).

Фиг. 7. График временного хода сейшевых колебаний высоты уровня на акватории (фиг. 4, точки 1-5).

Фиг. 8. График временного хода сейшевых колебаний фаз уровня на акватории (фиг. 4, точки 1-5).

Традиционные показатели ветро-волнового режима, такие как повторяемость штормовых (неблагоприятных) условий недостаточны для адекватного планирования сложных морских транспортных операций. Для обеспечения безопасности и повышения эффективности операций по буксировке или транспортировке крупных объектов, оценки времени ожидания благоприятных условий, планирования перехода, выбора пунктов штормового отстоя, выбора скорости перехода и соответственно состав сил и средств для той или иной морской транспортной операции требуется знать характеристики окон погоды. К числу основных характеристик окон погоды относятся число окон погоды заданной непрерывной продолжительности той или иной обеспеченности, среднее и максимальное время ожидания окна погоды заданной обеспеченности в заданный месяц или сезон.

Для получения статистических оценок характеристик окон погоды лучше всего использовать результаты реанализа полей ветра и волнения за продолжительный период времени длительностью несколько десятков лет. Реализация такого подхода затруднена ввиду недостатка данных реанализа.

Известно несколько подходов к моделированию штормов и окон погоды по волновым условиям (Матушевский Г.В., Надеев В.В. Статистические закономерности распределения характеристик устойчивости ветрового волнения, Метеорология и гидрология, №9. 1987, с. 70-76. Надеев В.В. Имитационное моделирование рядов ветрового волнения для определения продолжительности штормовых циклов, в сборнике Проблемы исследования и математического моделирования ветрового волнения, под общей редакцией проф. Давидана И.Н., СПб.: Гидрометеоиздат, 1995, 432 с. Рожков В.А., Лопатухин Л.И., Лавренов И.В., Дымов В.И., Бухановский А.В. Моделирование штормового волнения. // Изв. РАН. Физ. атмосферы и океана. 2000, т. 36, №5, с. 689-699). Однако вероятностная модель волнения основана на теории периодически коррелированного случайного процесса (ПКСП). Эта модель позволяет генерировать ансамбль временных рядов среднемесячных значений высот волн в ПКСП приближении, которые в дальнейшем используются как переменный во времени уровень z, на который накладывается модель штормов и окон погоды в виде импульсного случайного процесса. Построение и реализации такого подхода требует детального вероятностного анализа режима штормового волнения и вызывает затруднения при практической реализации.

В предлагаемом техническом решении моделирование штормов и окон погоды основано на методе имитационного моделирования штормов и окон погоды (Мастрюков С.И. Имитационное моделирование временных рядов штормов и окон погоды по ветровым условиям // Метрология и гидрология, №4. 2013, с. 58-67 [4]). При этом подходе в качестве исходных данных о состоянии природной среды достаточно иметь сведения об интегральной повторяемости штормов, которые приведены в многочисленных пособиях по режиму ветра и волнения. Для построения модели используются сведения о статистических связях повторяемости штормов со средними значениями количества штормов и их непрерывной продолжительности, а также статистические связи между функциями распределения числа штормов и их непрерывной продолжительности со средними значениями количества штормов и их непрерывной продолжительности.

При этом поле ветра может быть рассчитано по архиву полей приземного давления Европейского центра среднесрочных прогнозов погоды (ECMWF).

Путем анализа данных о штормах на акватории Норвежского, Баренцева и Белого морей (с. 58-67 [4]) получена следующая связь между средней непрерывной продолжительностью шторма τ и вероятностью штормовых условий P.

τ = 33 − ln P − 6.5,   0.001 < P < 0.5.                                                                                                 ( 1 )

В формуле (1) средняя непрерывная продолжительность шторма измеряется в часах, вероятность шторма P - в долях единицы. При повторяемости шторма 0.1% средняя непрерывная продолжительность шторма составляет 6 часов, что соответствует дискретности использованных 4-х срочных результатов реанализа. При вероятности шторма 50% средняя непрерывная продолжительность шторма составляет 33 часа. Средняя квадратическая невязка полученной оценки τ составляет 1.5 часа, максимальное отклонение от «фактической» средней непрерывной продолжительности не превышает 5 часов.

Среднее число штормов N за период продолжительностью T часов при известной средней непрерывной продолжительности шторма τ рекомендуется оценивать по формуле:

N = T P τ = T P − ln P 33 − 6.5 − ln P                                                                                                                                         ( 2 )

В формуле (2) T и τ измеряются в часах, P - в долях единицы.

При анализе периодов продолжительностью 1 месяц, при повторяемости шторма P=0.1% среднее число штормов в месяц составляет 0.1. То есть за 1 месяц шторм будет наблюдаться 1 раз в 10 лет. При возрастании вероятности шторма до 50% среднее число штормов достигает 11 в месяц.

Далее были получены эмпирические кривые плотности распределения числа штормов, полученные для 8 точек на акватории Норвежского, Баренцева и Белого морей за период с 1975 по 2002 годы.

Анализ эмпирических функций распределения числа штормов показал, что двухпараметрическая функция распределения Вейбулла (Матушевский Г.В., Надеев В.В. Статистические закономерности распределения характеристик устойчивости ветрового волнения. Метеорология и гидрология, №9. 1987, с. 70-76. Надеев В.В. Имитационное моделирование рядов ветрового волнения для определения продолжительности штормовых циклов, в сборнике: Проблемы исследования и математического моделирования ветрового волнения, под общей ред. проф. Давидана И.Н., СПб.: Гидрометеоиздат, 1995, 432 с. Рожков В.А., Лопатухин Л.И., Лавренов И.В., Дымов В.И., Бухановский А.В. Моделирование штормового волнения. // Изв. РАН. Физ. атмосферы и океана. 2000, т. 36, №5, с. 689-699), хорошо аппроксимирует распределение числа штормов при повторяемости штормов до 20%. При повторяемости штормов от 20 до 50% вместо функции распределения Вейбулла следует использовать нормальный закон распределения.

Для аппроксимации эмпирической функции распределения числа штормов n была использована модифицированная функция распределения Вейбулла, имеющая для плотности распределения f(n) и интегральной функции распределения F(n) вид:

f ( n ) = α ( n + 1 β ) α − 1 ⋅ 1 β exp [ − ( n + 1 β ) α ] P ( N < n ) = F ( n ) = 1 − exp [ − ( n + 1 β ) α ] ,   n > = 0                                                                                                                                                 ( 3 )

Параметры распределения Вейбулла α и β связаны со средним и дисперсией числа штормов соотношениями:

С р е д н е е = β ⋅ Г ( 1 α + 1 ) − 1 . Д и с п е р с и я = β 2 [ Г ( 2 α + 1 ) − ( Г ( 1 α + 1 ) ) 2 ] ,

где Г(х) - гамма- функция.

Эмпирическая функция распределения непрерывной продолжительности штормов удовлетворительно аппроксимируется модифицированной экспоненциальной функцией распределения с одним параметром λ.

Плотность распределения f(t) и интегральная функция F(t) модифицированного экспоненциального распределения непрерывной продолжительности штормов t при дискретности временного ряда Δt имеют вид:

f ( t ) = λ exp [ − λ ( t Δ t − 1 ) ] ,   … t ≥ Δ t ,   … λ > 0 F ( t ) = 1 − exp [ − λ ( t Δ t − 1 ) ]                                                                                                                                                                   ( 4 )

При этом параметр экспоненциального распределения λ связан со средней непрерывной продолжительностью шторма τ и дискретностью ряда Δt соотношением:

λ = Δ t τ .

Таким образом, используя модифицированное однопараметрическое экспоненциальное распределение, определив по данным о повторяемости штормовых условий с применением (1) среднюю непрерывную продолжительность шторма, можно рассчитать функцию распределения непрерывной продолжительности штормов.

Среднеквадратическая невязка между аналитической и эмпирической плотностями распределения непрерывной продолжительности штормов для вероятности шторма выше 5% не превышает 2.0%, максимальная невязка составляет 6.0%, что можно признать удовлетворительным.

Далее выполняется имитационное моделирование. Задачей имитационного моделирования является генерация значительного числа временных рядов заданной продолжительности, например сезон или месяц, на которых должны быть специальным образом распределено разное число временных промежутков разной непрерывной продолжительности, которые представляют собой штормовые периоды. Это должно быть сделано так, чтобы:

интегральная повторяемость штормовых условий (за 30-100 лет) соответствовала бы заданной повторяемости штормовых условий;

число штормов, определенное по совокупности генерируемых рядов, подчинялось бы выбранному закону распределения;

распределение непрерывной продолжительности штормов для каждого из генерируемых рядов подчинялась бы выбранному закону распределения.

По сведениям об интегральной повторяемости штормовых условий P оценивается среднее число штормов (2) и с использованием нормального распределения (при вероятности штормовых условий выше 20%) или распределения Вейбулла (3) определяется число рядов (лет) m с тем или иным количеством штормов.

По существу собственно имитационная модель основана на использовании генератора случайных чисел в диапазоне от первого до последнего номера члена генерируемого ряда для задания срока начала шторма. Окончание шторма определяется с учетом полученных оценок непрерывной продолжительности каждого из штормов. Значениям членов ряда на полученном участке присваивается значение, например, единица, что является признаком шторма. Если период нового шторма пересекается с периодом любого из ранее размещенных на временном отрезке штормов, срок начала шторма рассчитывается вновь с использованием того же генератора случайных чисел, если после 100 генераций случайных чисел это условие не выполняется, шторм «размещается» в любом месте временной последовательности.

На фиг. 1 в качестве иллюстрации приведены результаты имитации штормов и окон погоды для повторяемости (доверительной вероятности) штормовых условий 12.5%.

Таким образом, реализовав изложенные процедуры, получаем совокупность временных рядов штормов и окон погоды, статистические характеристики которых соответствуют известным климатическим сведениям о повторяемости штормов и статистическим закономерностям распределения их количества и непрерывной продолжительности.

На фиг. 2 приведен пример временного хода скорости ветра (а) и соответствующая ему временная развертка штормов и окон погоды (б). Обычно под окном погоды понимают промежуток времени любой продолжительности, в пределах которого скорость ветра меньше заданной. Для выполнения транспортных и других морских операций имеют значение только те окна погоды, продолжительность которых позволяет выполнить запланированную операцию или ее этап с соответствующими ограничениями по скорости ветра. Поэтому в практических реализациях под окнами погоды понимаются окна погоды заданной непрерывной продолжительности. Если непрерывная продолжительность благоприятных условий больше заданной непрерывной продолжительности операции в целое число раз, то именно это число принимается за число окон погоды в рассматриваемый промежуток времени. При заданной непрерывной продолжительности окна погоды на фиг. 2 выделяются 9 штормов и 4 окна погоды.

Приведенная модель позволяет генерировать временные ряды штормов и окон погоды, совокупность которых отражает характерные особенности ветрового режима, включая повторяемость штормов и функции распределения их количества и непрерывной продолжительности. Данная модель может быть использована для любых акваторий океана, поскольку функции распределения числа штормов и их непрерывной продолжительности являются производными от повторяемости штормовых условий. Модель пригодна для расчета статистических характеристик окон погоды при планировании сложных морских транспортных операций.

Далее определяют пространственное распределение фазы колебаний акватории по измерениям высоты уровня моря посредством альтиметрических спутников с выделением приливных и сейшивых колебаний уровня моря, что необходимо для снижения рисков, связанных с функционированием морских объектов хозяйственной деятельности в условиях резких колебаний уровня моря.

Отнесение наблюдаемых колебаний уровня моря к некоторому классу пространственных колебаний к классу прилива или сейш, является сложной задачей. Существует мнение, что колебания типа сейш можно идентифицировать по наличию противофазных колебаний в двух диаметрально противоположных точках акватории (Шулейкин В.В. Физика моря. - М: Наука, 1968, - 1083 с. Герман В.Х., Левиков С.П. Вероятностный анализ и моделирование колебаний уровня моря. - Л.: ГИМИЗ, 1988, - 231 с.). Однако для отнесения наблюдаемых колебаний уровня моря к классу сейш требуется больше точек наблюдений и использование других соотношений между колебаниями в них.

Традиционно понимается, что приливы - это бегущие волны, а сейши - стоячие волны. Такое толкование основано на видимом распространении волн. Часто в качестве механизма возникновения сейш используют представление о суперпозиции двух бегущих в противоположных направлениях приливных волн. Такие трактовки приливов и сейш, по существу, указывают на возможные объекты исследований, но не дают каких-либо методов изучения этих объектов.

Если следовать К. Трусделлу (Трусделл К. Первоначальный курс рациональной механики сплошных сред. М.: Мир, 1975, 592 с.), то волна это перемещающееся возмущение поверхности, форма которого не изменяется на интервале его длины. В таком случае отнести приливы к волнам нельзя. Действительно, длины приливных волн по оценкам океанологов составляют тысячи километров. Ни у кого не вызывает сомнения, что в Белом море существуют приливы. Длина его акватории значительно меньше длины волн прилива. Форма прилива в Белом море и точечно и по пространству значительно изменяется по площади моря, например, в районе Горла Белого моря наблюдаются три максимума в сутки, тогда как на остальной акватории - два, но и здесь амплитуда претерпевает значительные изменения.

Также принято считать, что приливы - это длинные волны. Однако на приливных картах океанов самые большие фазовые скорости прилива расположены у побережья на малых глубинах, а на больших глубинах, в центре океанов, расположены амфидромические области с малыми фазовыми скоростями. Это обстоятельство полностью противоречит следствию из теории длинных волн о том, что скорость фазы длинной волны пропорциональна глубине.

Сейши скор