Способ измерения дисперсии магнитного момента наночастицы в магнитной жидкости

Способ измерения дисперсии магнитного момента наночастицы в магнитной жидкости

Иллюстрации

Показать все

Реферат

Изобретение предназначено для контроля магнитных жидкостей, когда по условиям их применения недопустимо заметное различие размеров и магнитных моментов наночастиц. Например, в случае медицинского применения, когда частицы с большими магнитными моментами (крупные частицы) создают помеху кровотоку, а на частицы с малыми магнитными моментами со стороны магнитного поля действуют малые силы, недостаточные для их перемещения по кровяному руслу в нужное место организма, или в случае применения в качестве термометрических веществ, когда, как показано в литературе (Жерновой А.И. и др. Научное приборостроение, 2012, том 22, №3, с. 58-60), различие магнитных моментов приводит к зависимости константы Кюри от температуры.

Известен способ определения закона распределения магнитных моментов наночастиц в магнитной жидкости (магнитно-гранулометрический анализ). (Pshenichnicov A.F., Mekhonoshin V.V., Lebedev A.V. Magneto-granulometric analisis of concentrated ferrocolloids// Journal of Magnetism and Magnetic Materials, 1996, №161, p. 94-102.)

Способ состоит в произвольном выборе вида функции распределения (обычно логнормальной или гамма), выборе модели межчастичных взаимодействий (например, модели среднего действующего поля или Лоренца). На основе выбранной функции распределения и модели межчастичных взаимодействий производится теоретический расчет кривой намагничивания и ее сравнение с экспериментальной. При совпадении теоретической и экспериментальной кривых намагничивания, по функции распределения можно найти дисперсию распределения магнитных моментов наночастиц. Недостаток способа в его субъективности, так как выборы функции распределения и модели межчастичных взаимодействий являются произвольными. Другой недостаток в сложности проверки адекватности теоретической и экспериментальной кривых намагничивания. Этот метод можно принять за прототип.

Известен способ определения дисперсии размеров наночастиц в магнитной жидкости при помощи электронной микроскопии. (Ряполов П.А. Исследование структурных параметров нанодисперсных магнитных жидкостей // Научные ведомости. Серия Математика. Физика. 2011 №11(106). Вып.23.) В этом способе при помощи просвечивающего электронного микроскопа получают изображение наночастиц, содержащихся в пленке высушенной магнитной жидкости. Подсчетом количества частиц разного размера строят кривую распределения частиц по размерам, из которой можно определить дисперсию распределения. Так как магнитный момент частицы с поправкой на присутствие немагнитной аморфной фазы пропорционален ее объему, то по дисперсии распределения частиц по размерам можно найти дисперсию распределения по магнитным моментам. Недостаток метода в необходимости испарения жидкости при изготовлении образца, что может повлиять на распределении частиц по размерам в результате образования конгломератов. Другой недостаток в присутствии намагнитной фазы, которое уменьшает дисперсию распределения по магнитным моментам по сравнению с дисперсией распределения по размерам частиц.

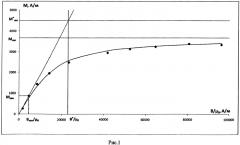
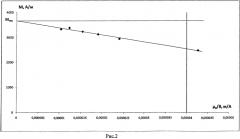
Предлагаемый способ не имеет указанных недостатков. В этом способе для измерения дисперсии магнитного момента парамагнитной наночастицы в магнитной жидкости получается экспериментальная зависимость намагниченности жидкости М от индукции магнитного поля В, представленная на рис. 1, по этой зависимости строится представленный на рис. 2 график зависимости M от (1/B), по которому при (1/B)=0 определяется намагниченность насыщения M_нас, а по формуле P_ср=кT/B[1-(M/M_нас)] среднее значение магнитного момента наночастиц P_ср на участке кривой намагничивания при намагниченности M, приближающейся к M_нас. Затем вычисляется значение индукции магнитного поля B*, при котором параметр Ланжевена После этого на начальном участке кривой намагничивания по экспериментальным точкам находится начальная магнитная восприимчивости æ_нач=(М_начµ_o/B_нач) (M_нач, B_нач - значения намагниченности и магнитной индукции на начальном участке кривой намагничивания) и определяется эффективная намагниченность насыщения M_нас*=(æ_начB*/µ₀)=æ_нач3кТ/P_ср. Дисперсия магнитных моментов находится по формуле: Д=(M_нас*-M_нас)(P_ср)²/М*.

Обоснование предлагаемого способа

Предлагаемый способ основан на том, что на начальном участке кривой намагничивания парамагнетика его намагниченность M по теории Ланжевена пропорциональна квадрату магнитного момента P парамагнитных частиц: M_нач=(nP²B/3kT), где n - концентрация частиц, B, T - индукция магнитного поля и температура, k - постоянная Больцмана. Намагниченность насыщения, измеряемая на конечном участке кривой намагничивания, пропорциональна магнитному моменту в первой степени: M_нас=nP. При наличии дисперсии магнитных моментов частиц измеряемые намагниченности M_нач и M_нас усредняются. В результате, получается M_нач=[n(P²)_срB/3кT], M_нас=nP_ср, где (P²)_ср и P_ср - средние значения P² и P. Так как значение магнитного момента конкретной частицы является случайной величиной, при любой функции распределения частиц по значениям P, дисперсию распределения Д можно находить по формуле Д=(P²)_ср-(P_ср)² (Д. Корн, Т. Корн, Справочник по математике, М. Наука, 1984, 832 с.), определив (P²)_ср и (P_ср)² по виду экспериментальной кривой намагничивания.

Для практического измерения Д предлагается следующий путь.

1) Получаем экспериментальную кривую намагничивания (зависимость намагниченности M от индукции магнитного поля B), представленную на рис. 1.

2) По значениям M и B на конечном участке кривой намагничивания строим зависимость M от (1/B), представленную на рис. 1 и 2, которая теоретически имеет вид M=M_нас-(nkT/B). По этой зависимости при (1/B)=0 экстраполяцией находим M_нас=nP_ср. (На рис. 1 и 2 M_нас обозначена горизонтальной прямой линией).

3) По зависимости M от (1/B), воспользовавшись тем, что M_нас-M=(nкT/B), при некотором значении B находим nкT/B и, зная B, определяем концентрацию частиц

и средний магнитный момент частиц

4) Зная P_ср, находим значение индукции B=B*, при которой параметр Ланжевена

5) По имеющимся экспериментальным значениям M=M_нач и B=B_нач на начальном участке кривой намагничивания находим среднюю начальную магнитную восприимчивость æ_нач=M_начµ₀/B_нач и эффективное значение намагниченности насыщения M_нас*=(æ_начB*/µ₀), которое равно M_нас при P=((P²)_ср)0,5. (На рис. 1 M_нас* обозначено горизонтальной прямой линией). Подставив в M*=n(P²)_срB*/3кT значение B*=3кT/P_ср, получаем M_нас*=n(P²)_ср/P_ср, откуда (M_нас*/M_нас)=(P²)_ср/(P_ср)². В результате, дисперсия магнитного момента наночастицы

Проверка осуществимости предлагаемого способа

Для проверки осуществимости предлагаемого способа измерения дисперсии магнитного момента наночастицы в магнитной жидкости были исследованы четыре магнитные жидкости на основе магнетита, отличающиеся технологией синтеза, концентрацией твердой фазы и растворителем. Получение кривых намагничивания проводилось на экспериментальной установке, описанной ранее в работе (А.И. Жерновой, В.Н. Наумов, Ю.Р. Рудаков, Получение кривой намагничивания дисперсии парамагнитных наночастиц путем нахождения намагниченности намагничивающего поля методом ЯМР // Научное приборостроение, 2009, том 19, №3, с. 57-61), где намагниченность находилась по напряженности H и индукции B магнитного поля внутри магнитной жидкости, измеряемым датчиками ЯМР, расположенными снаружи образца:

M=(B/µ₀)-H.

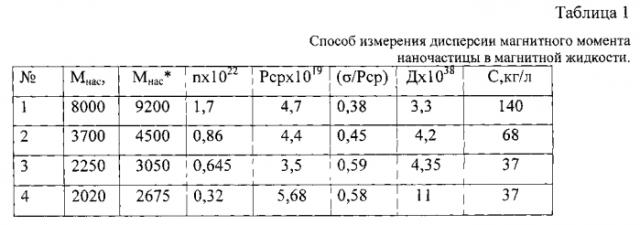
Полученные результаты приведены в таблице 1. Они показывают, что у всех исследованных жидкостей, независимо от концентрации и магнитного момента наночастиц, растворителя, технологии приготовления, разность M_нас*-M_нас, которая пропорциональна дисперсии, больше 1, что является предпосылкой осуществимости предлагаемого способа. Полученные значения дисперсии и среднеквадратичного отклонения магнитных моментов не противоречат здравому смыслу.

Способ измерения дисперсии магнитного момента наночастицы в магнитной жидкости путем получения зависимости намагниченности M от магнитной индукции B, определения намагниченности насыщения M_нас, определения при намагниченности М, приближающейся к M_нас, среднего магнитного момента наночастицы P_ср, определения начальной магнитной восприимчивости (M_нач, B_нач - намагниченность и магнитная индукция на начальном участке кривой намагничивания), отличающийся тем, что вычисляется значение эффективной намагниченности (к - постоянная Больцмана, T - температура), а дисперсия магнитного момента определяется по формуле .