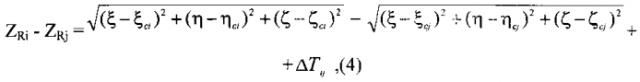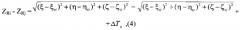Способ идентификации параметров навигационных спутников

Способ идентификации параметров навигационных спутников

Иллюстрации

Показать все

Реферат

Изобретение относится к способам навигации по Спутниковым Радионавигационным Системам (СРНС) и может быть использовано для идентификации параметров навигационных спутников и повышения точности определения координат навигационного приемника. Технический результат заключается в повышении точности определения координат навигационного приемника за счет исключения ошибок взаимной синхронизации часов навигационных спутников и навигационного приемника.

Известны различные способы повышения точности определения координат навигационного приемника. В [патент США No 7535414] изложен способ, который предполагает, что перед вычислением координат навигационного приемника производится разрешение неопределенностей, вызванных в т.ч. ошибками часов навигационных спутников, в неполных псевдодальностях. В [патент США No 6417801] предлагается разрешение неопределенностей в неполных псевдодальностях путем добавления в вектор оцениваемых параметров поправки ко времени измерения с последующим перебором всех допустимых целочисленных комбинаций неоднозначностей и выбором нужной из них по критерию минимума остаточных невязок.

Также для повышения точности определения координат навигационного приемника используются различные алгоритмы компенсации погрешностей часов [Интерфейсный контрольный документ ГЛОНАСС (5.1 редакция).- М.: РНИИ КП, 2008. - 57 с.], а также применяется дифференциальный режим измерений по кодовым дальностям, реализуемый с помощью контрольного навигационного приемника с известными географическими координатами - т.н. базовой станции [Bar-Sever, Y. A new Massachusetts model for GPS yawattitude // Journal of Geodesy, 70, 714723, 1996]. Недостатками данных способов являются сложность их реализации и невозможность точного определения текущих значений ошибок взаимной синхронизации часов навигационных спутников и навигационного приемника для их последующей компенсации.

Наиболее близким к предлагаемому изобретению является способ, описанный в [патент РФ №2432584. Способ определения координат навигационного приемника спутниковой радионавигационной системы / Васильев М.В., Михайлов Н.В., Поспелов С.С, Джалали Биджан], состоящий в том, что вычисление поправок к координатам приемника производится после измерения псевдодальностей и псевдоскоростей по невязкам псевдодальностей.

Недостатком данного способа является также сложность аппаратной и вычислительной реализации и невозможность точного определения текущих значений ошибок взаимной синхронизации часов навигационных спутников и навигационного приемника для их последующей компенсации.

Заявленное изобретение направлено на решение задачи повышения точности определения местоположения навигационного приемника за счет коррекции погрешности взаимной синхронизации часов навигационных спутников и навигационного приемника.

Поставленная задача возникает при разработке систем контроля и управления навигационными спутниками, а также использования их измерений для решения навигационной задачи объекта.

Для обеспечения идентификации параметров навигационных спутников и упрощения аппаратной и вычислительной реализации данной процедуры предлагается способ, состоящий в том, что в группе из двух навигационных спутников, находящихся в зоне прямой видимости, реализуются одновременные передача навигационных сообщений от каждого спутника к каждому, и их прием каждым спутником от каждого, определение межспутниковых псевдодальностей и их передача на другой спутник с последующим решением на каждом спутнике системы двух линейных алгебраических уравнений, в результате которого определяются истинные дальности между спутниками и погрешности взаимной синхронизации их часов, после чего погрешности взаимной синхронизации часов спутников передаются в навигационных сообщениях и компенсируются в навигационном приемнике при определении ортодромических координат навигационного приемника на основе решения алгебраического уравнения четвертой степени, сформированного по разности измеренных псевдодальностей объекта между двумя спутниками и параметрам ортодромической траектории объекта.

Точность решения навигационной задачи с использованием средств спутниковой навигации в значительной мере зависит от степени подавления помех, возникающих при приеме-передаче спутниковых сообщений. В общем случае информационная структура спутникового измерения псевдодальности Z_R, используемого в качестве основного сигнала при позиционировании объектов, с учетом помех, в наибольшей степени влияющих на точность позиционирования, имеет вид:

где ξ_с, η_c, ζ_с - текущие координаты спутника в гринвичской системе координат (ГрСК),

ξ, η, ζ - текущие координаты объекта в ГрСК,

С - номинальное значение скорости света в вакууме,

Δτ - погрешность часов навигационного приемника,

ΔT - погрешность часов спутника,

W_ИТ - погрешности, обусловленные прохождением радиосигнала через ионосферу и тропосферу,

W_П - инструментальные погрешности навигационного приемника.

Сигналы измерения псевдодальностей между i-м и j-м спутниками будут свободны от погрешностей, обусловленных прохождением сигнала через ионосферу и тропосферу, как в (1), и будут иметь вид:

где Z_ij - псевдодальность, измеренная на j-м спутнике,

R_ij - истинная дальность между i-м и j-м спутниками,

ΔT_j - погрешность часов j-го спутника,

ΔT_i - погрешность часов i-го спутника,

- погрешность, обусловленная ошибкой взаимной синхронизации часов i-го и j-го спутников.

Для определения погрешности, обусловленной ошибкой взаимной синхронизации часов i-го и j-го спутников, в каждом навигационном спутнике дополнительно реализуется возможность приема результатов измерений псевдодальностей между ним и спутниками, находящимися в прямой видимости. На фиг. 1 показана схема передачи результатов измерений псевдодальностей, где использованы обозначения: спутники 1_i, i=1,3.

Измеренные расстояния (псевдодальности) Z_ij между двумя навигационными спутниками 1 и 2 (фиг. 1) в соответствии с (2) могут быть представлены следующим образом:

где ΔТ₁₂, ΔT₂₁, - погрешности взаимной синхронизации часов спутников 1 и 2,

R₁₂ - истинная дальность между спутниками.

Учитывая очевидное соотношение:

система (3) из 2-х уравнений с 3-мя неизвестными; может быть сведена к системе 2-х уравнений с 2-мя неизвестными - истинной дальностью R₁₂ и погрешностью взаимной синхронизации часов спутников:

и легко решается непосредственно на борту каждого из спутников.

В данном случае решается задача текущего определения погрешностей взаимной синхронизации часов всех спутников и расстояний между спутниками, используемых, в свою очередь, в качестве дополнительной информации для повышения точности измерения текущего местоположения спутников.

Компенсация погрешностей взаимной синхронизации часов спутников и навигационного приемника основана на том, что для решения навигационной задачи спутниковые сообщения принимаются, как правило, не менее, чем от четырех спутников, что позволяет формировать различные линейные комбинации сигналов, принимаемых от разных спутников. Так, разность сигналов псевдодальностей, принятых от двух спутников - i-го и j-го, с учетом (1) имеет вид:

где принято вытекающее из практики спутниковой навигации допущение об идентичности помех, обусловленных прохождением через ионосферу и тропосферу радиосигналов спутников, находящихся в зоне видимости одного и того же объекта.

Как видно из (4), разность сигналов Z_Ri - Z_Rj любых двух спутников содержит помеховую составляющую ΔT_ij, которая уже известна из принятого спутникового сообщения и может быть скомпенсирована (при этом разность сигналов не содержит остальных помех, приведенных в (1): ошибок часов приемника, его инструментальных погрешностей и др.). В результате, обработке подлежат сигналы, содержащие только истинную информацию о координатах объекта:

что позволяет при его движении по аналитическим траекториям (локсодромической или ортодромической), аппроксимирующим реальную траекторию объекта со сколь угодно заданной точностью [Соколов С.В. Синтез аналитических моделей пространственных траекторий и их применение для решения задач спутниковой навигации // Прикладная физика и математика, т. 1, вып. 2, 2013. - С. 3-12], сделать решение навигационной задачи практически точным. Рассмотрим подобную возможность на примере ортодромической траектории.

Используя найденную в [Соколов С.В. Синтез аналитических моделей пространственных траекторий и их применение для решения задач спутниковой навигации // Прикладная физика и математика, т. 1, вып. 2, 2013. - С. 3-12] взаимосвязь гринвичских координат на ортодромической траектории:

ξ = cos P 0 ⋅ P ⋅ η − sin P 0 ⋅ a 0 ⋅ a 1 − η 2 , ζ = sin P 0 ⋅ P ⋅ η + cos P 0 ⋅ a 0 ⋅ a 1 − η 2 ,       ( 6 )

h - высота спутника, r - радиус Земли, Р, Р₀ - параметры, зависящие от координат начальной к конечной точек ортодромической траектории и приведенные в [Соколов С.В. Синтез аналитических моделей пространственных траекторий к их применение для решения задач спутниковой навигации // Прикладная физика и математика, т. 1, вып. 2, 2013. - С. 3-12],

и приводя переменные с учетом движения объекта по поверхности Земли (т.е.), преобразуем уравнение (5) к следующему виду:

Δ Z i j = Θ 1 t i + Θ 2 t i η + Θ 3 t i a 1 − η 2 − Θ 1 t j + Θ 2 t j η + Θ 3 t j a 1 − η 2 ,   ( 7 )

где

- известные нестационарные функции. Очевидно, что в этом случае задача определения координатного вектора сводится к решению иррационального уравнения (7) относительно неизвестной переменной η. Трижды последовательно возводя обе части уравнения (7) в квадрат и обозначая параметры уравнения как:

получаем в канонической форме уравнение четвертого порядка относительно координаты η:

все коэффициенты которого нестационарны и должны вычисляться в масштабе времени поступления спутниковых измерений (что для существующих вычислителей проблемы не представляет.) Принципиально важным преимуществом уравнения (8) является известная возможность его аналитического решения [Г. Корн, Т. Корн. Справочник по математике для научных работников и инженеров. М.: Наука, 1975, 720 с.], позволяющая, во-первых, исключить все ошибки позиционирования, связанные с погрешностями применяемых в настоящее время численных методов, а во-вторых, повысить быстродействие решения навигационной задачи за счет ухода от итеративных процедур определения координатного вектора. Т.к. особенностью решения уравнения (8) является его неоднозначность, выраженная в неизбежном существовании четырех решений, определяемых по известным формулам [Г. Корн, Т. Корн. Справочник по математике для научных работников и инженеров. М.: Наука, 1975, 720 с.], то для определения истинного значения координаты η объекта очевидным выходом является привязка ее текущего значения к значению, полученному в предыдущий момент времени. В силу того, что начальные значения координат ортодромической траектории известны реализация подобной процедуры сравнения никаких трудностей не представляет.

Алгоритм реализации предложенного способа рассмотрим по шагам на примере спутника 1.

1. Передача навигационных сообщений к спутнику 2.

2. Прием навигационных сообщений от спутника 2 (выполняется одновременно с п. 1).

3. Определение псевдодальности Z₂₁ до спутника 2.

4. Передача полученного значения псевдодальности Z₂₁ на спутник 2.

5. Прием значения псевдодальности Z₁₂ от спутника 2 (выполняется одновременно с п. 4).

6. Решение системы уравнений (3) и вычисление истинной дальности R₁₂ и погрешности взаимной синхронизации часов ΔТ₁₂.

7. Передача в спутниковом навигационном сообщении погрешностей взаимной синхронизации часов ΔТ₁₂.

8. Вычисление в навигационном приемнике разностей псевдодальностей по измерениям, принятым от каждой пары видимых спутников.

9. Вычитание из полученных разностей псевдодальностей погрешностей взаимной синхронизации часов.

10. Вычисление текущих значений коэффициента уравнения (8).

11. Решение уравнения (8) и вычисление координат объекта по соотношениям (6).

Предложенный способ идентификации параметров навигационных спутников позволяет, во-первых, существенно повысить точность синхронизации хода часов на всех навигационных спутниках группировки (что особенно важно для системы ГЛОНАСС, наземные станции синхронизации времени которой расположены только на территории РФ), во-вторых, повысить общую точность решения навигационной задачи за счет компенсации основных помех в принятом навигационном сообщении. При этом также неизбежно увеличение точности определения рассмотренных пространственно-временных параметров в силу большей точности межспутниковых измерений, осуществляемых в космосе, по сравнению с телеметрическими, подверженными влиянию атмосферных возмущений.

Способ идентификации параметров навигационных спутников, заключающийся в том, что в группе из двух навигационных спутников, находящихся в зоне прямой видимости, реализуются одновременные передача навигационных сообщений от каждого спутника к каждому, и их прием каждым спутником от каждого, определение межспутниковых псевдодальностей, и их передача на другой спутник, с последующим решением на каждом спутнике системы двух линейных алгебраических уравнений, в результате которого определяются истинные дальности между спутниками и погрешности взаимной синхронизации их часов, после чего погрешности взаимной синхронизации часов спутников передаются в навигационных сообщениях и компенсируются в навигационном приемнике при определении ортодромических координат навигационного приемника на основе решения алгебраического уравнения четвертой степени, сформированного по разности измеренных псевдодальностей объекта между двумя спутниками и параметрам ортодромической траектории объекта.