Способ измерения параметров распределения эритроцитов по деформируемости

Способ измерения параметров распределения эритроцитов по деформируемости

Иллюстрации

Показать все

Реферат

Предлагаемое изобретение относится к способам в медицинской диагностической технике, предназначенным для измерения деформируемости красных клеток крови. В отличие от существующих аналогов, основанных на принципе лазерной дифрактометрии, предлагаемый способ позволяет измерять не только среднюю деформируемость эритроцитов, но и параметры распределения клеток крови по деформируемости, а именно дисперсию (разброс) деформируемости и асимметрию распределения эритроцитов по деформируемости в исследуемом образце крови. Измерение и постоянный контроль этих параметров важен для диагностики и лечения целого ряда заболеваний, в том числе таких распространенных заболеваний как острые нарушения мозгового кровообращения, артериальная гипертония и сахарный диабет. Работоспособность предлагаемого устройства проверена на специально подготовленных образцах крови крыс.

Деформируемость эритроцитов есть мера способности клеток крови изменять свою форму под действием внешних сил. Известно, что деформируемость эритроцитов является одним из основных микрореологических параметров крови [1-3]. Для диагностики и лечения многих заболеваний необходимо иметь возможность постоянно контролировать этот параметр. Деформируемость эритроцитов важно контролировать и в донорской крови в процессе ее хранения на станциях переливания крови [4]. В настоящее время известно несколько способов измерения деформируемости эритроцитов [5-8]. Это втягивание эритроцитов в микропипетку, растягивание эритроцитов лазерным пинцетом, видеосъемка эритроцитов, деформированных в сдвиговом потоке силами вязкого трения. Однако эти методы являются весьма сложными и трудоемкими. Кроме того, они требуют большого времени для измерений и обработки данных. Более простым методом является пропускание пробы крови под давлением через пористый фильтр. Однако этот метод требует значительного количества крови и не всегда дает надежные результаты.

Одним из наиболее удобных методов измерения деформируемости эритроцитов является лазерная дифрактометрия эритроцитов в сдвиговом потоке (эктацитометрия). Существуют разные типы эктацитометров [9-15]. Общим для этих приборов является то, что деформация эритроцитов осуществляется силами вязкого трения, а информация о форме частиц извлекается из дифракционной картины, возникающей при рассеянии лазерного пучка на суспензии эритроцитов. В ротационном эктацитометре [11] сильно разбавленную суспензию эритроцитов заливают в зазор между стенками двух прозрачных коаксиальных стаканов, один из которых неподвижен, а другой может вращаться со ступенчато изменяемой угловой скоростью (так называемая ячейка Куэтта). Вращение подвижного стакана вызывает течение жидкости и появление в ней сдвиговых напряжений, которые ориентируют эритроциты определенным образом и вытягивают их в направлении потока. Для наблюдения за изменением формы частиц суспензию просвечивают лазерным пучком. Пучок рассеивается на эритроцитах и дает на экране наблюдения дифракционную картину, которая содержит в себе информацию о форме исследуемых частиц. При малых скоростях вращения подвижного стакана центральное дифракционное пятно имеет круглую форму, а при больших скоростях оно становится эллиптическим, что свидетельствует о выстраивании эритроцитов в сдвиговом потоке и вытягивании их в направлении потока под действием сил вязкого трения.

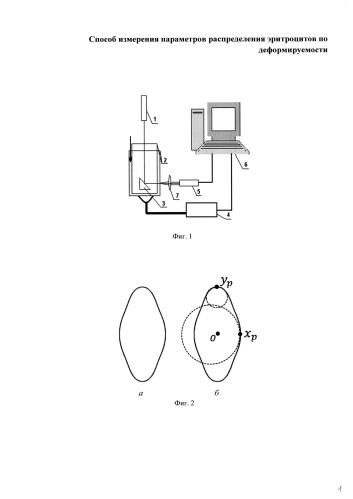
Схема лазерного эктацитометра эритроцитов показана на Фиг. 1, где 1 - лазер, 2 - ячейка Куэтта, 3 - зеркало, 4 - двигатель, 5 - видеокамера, 6 - персональный компьютер, 7 - линза.

Дифракционную картину снимают на видеокамеру и в цифровом виде передают в компьютер, где она обрабатывается по определенному алгоритму. Обычная процедура обработки данных состоит в следующем [2]. Компьютер выбирает на экране наблюдения точки, в которых интенсивность рассеянного света имеет некоторое определенное значение. Эти точки образуют линию, называемую линией изоинтенсивности. Как правило, эту линию выбирают на периферии центрального дифракционного максимума. Затем линию изоинтенсивности аппроксимируют эллипсом. Измеряют большую (y_p) и малую (x_p) полуоси эллипса и вычисляют параметр

называемый параметром (индексом) деформируемости эритроцитов. Такие измерения повторяют при нескольких скоростях вращения подвижного стакана. В результате получают зависимость параметра деформируемости эритроцитов от сдвигового напряжения - так называемую функцию деформируемости или кривую деформируемости эритроцитов. Эта кривая выглядит по-разному для разных образцов крови. В частности, у пациентов с острым нарушением мозгового кровообращения деформируемость эритроцитов заметно ниже, чем у здоровых людей такого же возраста [16]. В этом и в других случаях лазерная эктацитометрия эритроцитов позволяет выявить реологическое нарушение, оценить его степень и подобрать адекватное лечение. Подобные анализы необходимы при серповидно-клеточной анемии, наследственном сфероцитозе и малярии. В последние годы появляется все больше свидетельств того, что контроль деформируемости эритроцитов необходим при лечении таких социально значимых заболеваний как ишемия, артериальная гипертония и сахарный диабет. Достоинствами лазерной эктацитометрии по сравнению с другими методами измерения деформируемости эритроцитов являются простота, быстрота измерений и обработки данных, возможность получения данных сразу для больших ансамблей частиц при использовании минимальных количеств крови (2-3 микролитра).

Лазерная эктацитометрия эритроцитов была предложена в 1975 году Бессис и Мохандас [17-19] и с тех пор используется без существенных изменений, позволяя измерять лишь среднюю деформируемость эритроцитов в исследуемом образце крови. Однако в крови здорового, а тем более больного человека, разные эритроциты имеют разную способность к деформации [7, 8, 20, 21]. Это дает основание рассматривать деформируемость как статистическую характеристику ансамбля эритроцитов и использовать для ее описания такие понятия как функция распределения, среднее значение, дисперсия и т.п.

Цель настоящего изобретения - найти способ измерения этих параметров, используя для этого принцип лазерной эктацитометрии.

Техническим результатом является возможность измерять новые параметры - дисперсию деформируемости эритроцитов и асимметрию распределения эритроцитов по деформируемости, получение более точного рецепта измерения основной измеряемой величины, а именно, средней деформируемости эритроцитов в исследуемом образце крови.

Технический результат достигается тем, что способ измерения параметров распределения эритроцитов по деформируемости состоит в видеозаписи и обработке дифракционной картины, возникающей при рассеянии лазерного пучка на разбавленной суспензии эритроцитов, деформированных в сдвиговом потоке силами вязкого трения, оцифровке этой дифракционной картины, определении формы линии изоинтенсивности, лежащей на периферии центрального дифракционного максимума, измерении интенсивности I рассеянного света на данной линии изоинтенсивности по отношению к интенсивности центрального дифракционного максимума I(0), определении координат полярных точек x_p и y_p, лежащих на пересечении данной линии изоинтенсивности с горизонтальной осью координат и с вертикальной осью координат, а также радиусов кривизны R(x_p) и R(y_p) данной линии изоинтенсивности в указанных полярных точках с последующим вычислением средней деформируемости эритроцитов s, дисперсии деформируемости эритроцитов µ, а также коэффициента асимметрии распределения эритроцитов по деформируемости ν по следующим формулам:

,

,

,

где x_p - координата полярной точки, лежащей на пересечении данной линии изоинтенсивности с горизонтальной осью координат;

y_p - координата полярной точки, лежащей на пересечении данной линии изоинтенсивности с вертикальной осью координат;

- числовой параметр;

R(x_p) и R(y_p) - радиусы кривизны данной линии изоинтенсивности в указанных полярных точках.

Нами был разработан метод, в котором эритроциты в сдвиговом потоке рассматриваются как плоские эллиптические диски [16, 22, 23]. В отличие от модели эритроцитов как эллипсоидов [24, 25], модель плоских дисков дает возможность в аналитической форме найти связь между параметрами дифракционной картины и характеристиками ансамбля эритроцитов. Основанием для нашей модели является изображение эритроцитов в сдвиговом потоке, полученное с помощью микроскопа [7, 8]. Кроме того, как показано в работе [23], модель плоских дисков дает достаточно высокую точность в области малых углов рассеяния, используемой в лазерной эктацитометрии эритроцитов.

Полуоси дисков а и b мы считаем случайными величинами и определяем формулами

Здесь a ₀ и b₀ - средние размеры полуосей, ε - случайный параметр формы. Такая модель позволяет описать ансамбль эритроцитов с учетом того, что разные клетки обладают разной способностью к деформации. Характеристиками ансамбля эритроцитов в нашей модели являются средняя деформируемость эритроцитов s, дисперсия деформируемости µ и коэффициент асимметрии распределения эритроцитов по деформируемости ν. Эти величины определяются формулами

На основе проведенного анализа нам удалось найти связь этих характеристик с параметрами дифракционной картины, которые могут быть измерены с помощью лазерного эктацитометра. Таким параметрами дифракционной картины являются следующие

D = y p x p ,  C 1 = x p R ( x p ) ,  C 2 = y p R ( y p ) .                                                 ( 4 )

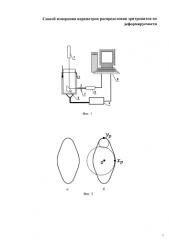
Здесь x_p - координата полярной точки, лежащей на пересечении данной линии изоинтенсивности с горизонтальной осью координат, y_p - координата полярной точки, лежащей на пересечении данной линии изоинтенсивности с вертикальной осью координат, R(x_p) - радиус кривизны данной линии изоинтенсивности в первой из указанных полярных точек, R(y_p) - радиус кривизны данной линии изоинтенсивности во второй из указанных полярных точек. Пример линии изоинтенсивности (а), полярные точки этой линии, а также круги кривизны линии изоинтенсивности, построенные в полярных точках (б), показаны на Фиг 2.

Уравнения, связывающие между собой параметры (2) и (3), имеют вид

D / s = 1 + ν ⋅ q 0 ,                                                                                   ( 5 )

Здесь параметры q₀, q₁, q₂ определяются формулами

где I - интенсивность рассеянного света на некоторой линии изоинтенсивности, расположенной вблизи границы центрального дифракционного максимума и выбранной для измерений, I(0) - интенсивность центрального максимума дифракционной картины, β= -0,4 - постоянная величина (параметр функции Бесселя).

Подставляя β= -0,4 в формулу (8), получаем числовой параметр, характеризующий отношение интенсивности I на данной линии изоинтенсивности к I(0). Решение уравнений (4)-(6) имеет вид

где числовые параметры

Подставляя в формулу (9) значения параметров из (8) и (10), она примет следующий вид:

,

Заметим, что параметры D, C₁, C₂, ƒ₀ могут быть найдены экспериментально в опыте по лазерной эктацитометрии эритроцитов. После этого параметры s, µ, ν могут быть вычислены по формулам (7)-(9). Тем самым поставленная задача решена: параметры распределения эритроцитов по деформируемости найдены на основе данных лазерной дифрактометрии эритроцитов.

Отметим еще одно важное обстоятельство. При обычном способе измерения деформируемости эритроцитов считается, что средняя деформируемость эритроцитов определяется параметром D=y_p/x_p, равным отношению полуосей линии изоинтенсивности. Как показывает проведенный нами анализ, это не всегда так. Из уравнения (5) видно, что параметр D совпадает со средней деформируемостью эритроцитов s=a ₀/b₀ только при условии ν=0, т.е. в случае симметричного распределения эритроцитов по деформируемости. Согласно уравнению (5), в общем случае параметры S и D отличаются друг от друга, причем это отличие тем сильнее, чем больше асимметрия распределения эритроцитов по деформируемости (ν) и чем меньше уровень интенсивности рассеянного света на линии изоинтенсивности, выбранной для измерений. Таким образом, предлагаемый нами способ измерения параметров распределения эритроцитов по деформируемости не только позволяет измерять новые параметры - дисперсию деформируемости эритроцитов и асимметрию распределения эритроцитов по деформируемости, но и дает более точный рецепт измерения основной измеряемой величины, а именно, средней деформируемости эритроцитов в исследуемом образце крови. Алгоритм обработки данных лазерной эктацитометрии эритроцитов, выражаемый формулами (8)-(10), мы назвали алгоритмом кривизны линии изоинтенсивности.

Другой способ оценки параметров s, µ, ν (способ подгонки) состоит в том, чтобы использовать полученное нами аналитическое выражение для формы линии изоинтенсивности, лежащей вблизи границы центрального дифракционного максимума. Это выражение имеет вид

Здесь r, φ - обобщенные полярные координаты, определяемые формулами

x, y - декартовы координаты точки на экране наблюдения. Параметры

представляют собой величины, определяющие размеры дифракционной картины (т.е. расстояния от центра картины до первого дифракционного минимума) по вертикали и по горизонтали соответственно. Остальные параметры в формуле (13) имеют следующий смысл: z - расстояние от измерительного объема до экрана наблюдения, k=2π/λ - волновое число, λ - длина световой волны, a ₀ и b₀ - средние размеры полуосей эритроцитов в сдвиговом потоке эктацитометра, рассчитываемые по указанной выше формуле (13), исходя из значений А и В, q₁=3.82 - постоянная величина (параметр функции Бесселя). Способ подгонки состоит в том, чтобы подобрать величины параметров s, µ, ν исходя из условия наилучшего совпадения линии изоинтенсивности, полученной экспериментально и построенной теоретически по формуле (11).

Пример 1.

Для проверки работы алгоритма кривизны линии мы провели специальные исследования. Эксперименты проводились с эритроцитами крысы на приборе ЛАДЭ 6 (Реомедлаб, Россия). Дифракционные картины были получены для бимодальных ансамблей эритроцитов, т.е. ансамблей, состоящих из частиц всего лишь двух типов (форм). Экспериментально такие ансамбли создавались путем обработки части клеток раствором глютаральдегида, уменьшающим их деформируемость.

Полученные данные представлены на Фиг. 3. На этой фигуре показаны 4 линии изоинтенсивности, полученные с четырьмя разными образцами крови. Все линии относятся к одной и той же сдвиговой скорости, равной 2075 с^-1, и к одинаковому уровню интенсивности рассеянного света, а именно

I / I ( 0 ) = 0.05.                                                                                             ( 14 )

Разные линии соответствуют разной концентрации клеток, обработанных раствором глютаральдегида. Содержание таких клеток в исследованных образцах крови характеризуется числами (в процентах): 0 (слева вверху), 20 (справа вверху), 50 (слева внизу), 100 (справа внизу). Для анализа мы выбрали одну из этих линий, а именно, линию, показанную на Фиг. 3 вверху справа. Для этой линии экспериментально заданные значения параметров s, µ, ν таковы:

Оценки этих же параметров, полученные с помощью алгоритма кривизны линии изоинтенсивности, выражаются числами

Процедура обработки дифракционной картины показана на Фиг. 4. Здесь на «а» показана дифракционная картина, на «б» - линия изоинтенсивности, выбранная вблизи границы центрального дифракционого максимума и соответствующая условию (14), на «в» - сглаженная линия изоинтенсивности, на «г» - та же линия, ее полярные точки и круги кривизны, построенные в этих точках. Сопоставление данных (15) и (16) показывает, что алгоритм кривизны линии изоинтенсивности обеспечивает удовлетворительную точность измерений.

Пример 2.

Мы провели аналогичные измерения и для другой сдвиговой скорости. Результаты представлены на Фиг. 5. На этой фигуре показаны 4 линии изоинтенсивности, полученные с четырьмя разными образцами крови. Все линии относятся к одной и той же сдвиговой скорости, равной 660 с^-1, и к одинаковому уровню интенсивности рассеянного света, определяемому формулой (14). Разные линии соответствуют разной концентрации клеток, обработанных раствором глютаральдегида. Содержание таких клеток в исследованных образцах крови характеризуется числами (в процентах): 0 (а), 20 (б), 50 (в), 100 (г). Для анализа мы выбрали одну из этих линий, а именно, линию, показанную на фиг. 5б. На Фиг. 6 показаны дифракционная картина (а), линия изоинтенсивности (б) и процедура обработки этой линии (в).

Для этой линии экспериментально заданные значения параметров s, µ, ν таковы:

Оценки этих же параметров, полученные с помощью алгоритма кривизны линии изоинтенсивности, выражаются числами

Таким образом, алгоритм кривизны линии изоинтенсивности дает точность измерения средней деформируемости эритроцитов, дисперсии деформируемости эритроцитов и асимметрии распределения эритроцитов по деформируемости, достаточную для практических приложений.

Литература

1. Левтов В.А., Регирер С.А., Шадрина Н.Х. Реология крови. М.: Медицина, 1982.

2. Фирсов Н.Н., Джанашия П.Х. Введение в экспериментальную и клиническую гемореологию. Москва, 2008.

3. Муравьев А.В., Чепоров С.В. Гемореология (экспериментальные и клинические аспекты реологии крови). Ярославль, 2009.

4. Michael Tarasev, Kenneth Alfano. Method to use ektacytometry to improve stored red blood cell or whole blood product utilization. Patent US 20110318773 A1 (2010).

5. Musielak M. Red blood cell-deformability measurement: Review of techniques. Clinical Hemorheology and Microcirculation, 2009, v. 42, pp. 47-64.

6. Youngchan Kim et el. Measurement Techniques for Red Blood Cell Deformability: Recent Advances - chapter 10 in the book "Blood Cell - An Overview of Studies in Hematology", ISBN 978-953-51-0753-8.

7. Dobbe J.G.G., Hardeman M.R., Streekstra G.J., Starckee J., Ince C., Grimbergen C.A. Analyzing red blood cell-deformability distributions. Blood Cells, Molecules, and Diseases 2002, v. 28, N 3, p. 373-384.

8. Dobbe J.G.G., Streekstra G.J., Hardeman M.R., Ince C., Grimbergen C.A. Measurement of the distribution of red blood cell deformability using an automated rheoscope. Cytometry (Clinical Cytometry) 2002 v. 50, p. 313.

9. Захаров С.Д. Устройство для определения деформируемости эритроцитов крови. Патент RU 2301617.

10. Васин Б.Л., Долгинов Я.Ш., Еремеев Б.В., Захаров С.Д., Симанов В.А., Косырев А.Б. Устройство для определения деформируемости эритроцитов (лазерный цитодифрактометр) АС №1697304, БИ №45 (1991).

11. Квартальнов Л.А., Фирсов Н.Н. Устройство для измерения агрегационного состояния и деформационного состояния эритроцитов и способ его применения. Патент RU 2403569.

12. Yun-He Ku. Apparatus for measuring blood cell deformability Patent US 20060119836 A1 (2003).

13. Clinical Hemorheology and Microcirculation, 1994, Vol. 14, pp. 605-618.

14. Белкин A.B. Марьинских B.B., Сайфиев P.P. Устройство для оценки деформабильности эритроцитов. Патент RU 2236009.

15. Сайфиев P.P. Исследование деформируемости эритроцитов млекопитающих с использованием усовершенствованного эктацитометра. Кандидатская диссертация. Тюмень, 2002.

16. Nikitin S.Yu., Priezzhev A.V., А.Е. Lugovtsov А.Е. Laser Diffraction by the Erythrocytes and Deformability Measurements. In: Advanced Optical Flow Cytometry: Methods and Disease Diagnoses. Edited by Valery V. Tuchin, Wiley-VCH Verlag 2011, pp. 133-154.

17. Bessis M., Mohandas N. A diffractometric method for the measurement of cellular deformability. Blood Cells, 1975, v. 1, p. 307-313.

18. Groner W., Mohandas N., Bessis M. New optical technique for measuring erythrocyte deformability with the ektacytometer. Clinical Chemistry, 1980, v. 26, N 9, p. 1435.

19. Bessis M., Mohandas N. Automated ektacytometry: A new method of measuring red cell indices and red cell quality. Blood Cells, 1980, Vol. 6, p. 315-327.

20. Streekstra G.J., Dobbe J.G.G., Hoekstra A.G. Quantification of the poorly deformable red blood cells using ektacytometry. Optics Express, 2010, v. 18, N 13, p. 14173.

21. Plasek J., Marik T. Determination of undeformable erythrocytes in blood samples using laser light scattering. Applied Optics, 1982, v. 21, N 23, p. 4335-4338.

22. Никитин С.Ю., Кормачева M.A., Приезжев A.B., Луговцов А.Е. Рассеяние лазерного пучка на неоднородном ансамбле эллиптических дисков, моделирующих красные клетки крови в эктацитометре. Квантовая электроника, 2013, т. 43, N 1, с. 90-93.

23. Nikitin S.Yu., Priezzhev A.V., Lugovtsov A.E.. Analysis of laser beam scattering by an ensemble of particles modeling red blood cells in ektacytometer. Journal of Quantitative Spectroscopy and Radiative Transfer, 2013, v. 121, pp. 1-8.

24. Streekstra G.J., Hoekstra A.G., Nijhof E.-J., Heethaar R.M. Light scattering by red blood cells in ektacytometry: Fraunhofer versus anomalous diffraction. Applied Optics, 1993, v. 32, N 13, p. 2266.

25. Streekstra G.J., Hoekstra A.G., Heethaar R.M. Anomalous diffraction by arbitrary oriented ellipsoids: application in ektacytometry. Applied Optics, 1994, v. 33, p. 7288.

Способ измерения параметров распределения эритроцитов по деформируемости, состоящий в видеозаписи и обработке дифракционной картины, возникающей при рассеянии лазерного пучка на разбавленной суспензии эритроцитов, деформированных в сдвиговом потоке силами вязкого трения, оцифровке этой дифракционной картины, определении формы линии изоинтенсивности, лежащей на периферии центрального дифракционного максимума, измерении интенсивности I рассеянного света на данной линии изоинтенсивности по отношению к интенсивности центрального дифракционного максимума I(0), определении координат полярных точек x_p и y_p, лежащих на пересечении данной линии изоинтенсивности с горизонтальной осью координат и с вертикальной осью координат, а также радиусов кривизны R (x_p) и R (y_p) данной линии изоинтенсивности в указанных полярных точках с последующим вычислением средней деформируемости эритроцитов s, дисперсии деформируемости эритроцитов µ, а также коэффициента асимметрии распределения эритроцитов по деформируемости v по следующим формулам: , где x_p - координата полярной точки, лежащей на пересечении данной линии изоинтенсивности с горизонтальной осью координат;y_p -координата полярной точки, лежащей на пересечении данной линии изоинтенсивности с вертикальной осью координат; - числовой параметр;R (x_p) и R (y_p) - радиусы кривизны данной линии изоинтенсивности в указанных полярных точках.