Эффективный способ выбора репрезентативного элементарного объема на цифровых представлениях пористых сред

Эффективный способ выбора репрезентативного элементарного объема на цифровых представлениях пористых сред

Иллюстрации

Показать все

Реферат

По настоящей заявке испрашивается приоритет в соответствии с 35 U.S.C. §119 (e) на основании предшествующей заявки на патент США №13/546,053, поданной 11 июля 2012 г., и предварительной заявки на патент США №61/618,265, поданной 30 марта 2012 г., которые включены в настоящее описание путем ссылки в полном объеме.

Уровень техники

Настоящее изобретение относится к способам и системам для прогнозирования свойств потока текучих сред через пористые среды, такие как пористая порода и, в частности, относится к таким способам и системам для выбора из цифрового представления гетерогенной пористой среды наиболее репрезентативного подобразца, чтобы использовать его для прогнозирования свойств, таких как пористость, проницаемость и/или похожих характеристик.

Цифровые представления пористых сред, таких как порода, кость, почва и другие материалы, могут быть произведены с помощью изображений сканирования рентгеновской компьютерной томографии, сканирующей электронной микроскопии, конфокальной микроскопии и другими способами. Такие цифровые представления полезны для характеризации пористых сред с применением компьютерного моделирования (Knackstedt, M.A., et al., "Digital Core Laboratory: Properties of Reservoir Core Derived from 3D Images", Society of Petroleum Engineers, 2004; and Vermeulen, J.P., "New Developments in FESEM Technology", Carl Zeiss nano-technology Systems Division, http://www.zeiss.com/C1256E4600307C70/EmbedTitelIntern/NewDevelopmentinFESEMTechnology/$FileNew_Development_FESEM_Technology.pdf).

Важной проблемой в цифровом моделировании характеристик пористых сред является размер образца. Многие образцы, представляющие практический интерес, такие как пористая порода, являются неоднородными, и для получения усредненных свойств для больших объемов пористых сред потребовалась бы оцифровка очень больших образцов. Многие из характеристик породы, такие как абсолютная проницаемость, требуют значительных вычислительных ресурсов для моделирования, и в результате объемы образца часто являются намного меньшими, чем интересующий объем для репрезентативной характеризации. Подобразца могут быть выбраны визуально обученным геологом, но этот подход является субъективным, и его результаты сильно различаются. Кроме того, деловые и технические решения, такие как инвестиции в скважины, планы перфорации скважин, оценки извлекаемых ресурсов и другие подобные решения, принимаемые на основании цифрового моделирования характеристик породы, часто влекут большие затраты. В результате существует потребность в устранении субъективности, погрешности и вариаций в характеристиках таких пористых сред.

Один из подходов к идентификации соответствующих подобразцов заключается в идентификации репрезентативного элементарного объема (REV). REV является наименьшим объемом, для которого может быть выполнено конкретное измерение, которое даст значение, репрезентативное для всего объема. Объемы, меньшие REV, демонстрируют вариацию в конкретном измерении, что делает образцы, меньшие REV, не подходящими для моделирования. Способ вычисления REV с использованием объемной пористости в качестве измерения описывается в литературе Bear (Bear, J., Dynamics of Fluids in Porous Media; General Publishing Company Ltd., Canada, 1972, p. 19-21). Множество способов, которые обозначаются как REV, в конечном счете не являются действительно «элементарными». То есть многие применяемые способы позволяют найти подобъемы большего объема, которые являются репрезентативными для большего объема, но способ может не выдавать наименьший возможный или элементарный объем.

Razavi и соавт. описывают общий подход к REV (Razavi, et al., "Representative Elementary Volume Analysis of Sands Using X-Ray Computed Tomography", Geotechnical Testing Journal, Vol. 30, No. 3, Paper ID GTJ100164, 2006). Блок-схема способа, описанного Razavi и соавт., показана на Фиг. 1. В способе, показанном Razavi и соавт., выбирается точка приблизительно в центре образца, и затем анализируется сферический объем подобразца вокруг этой центральной точки. Свойства образца вычисляются для сферического подобразца. Радиус подобразца увеличивается, и свойства вычисляются повторно. Радиус подобразца увеличивается пошагово, пока не будет достигнут REV. У этого способа имеется множество недостатков. Он может не давать подходящего результата в определенных неоднородных образцах. Хотя он и может выдать приемлемый RV, он может не выдать REV. Как было указано выше, завершение проводимых вычислений на цифровых представлениях образцов породы может потребовать значительного количества машинного времени, поэтому определение наименьшего REV в образце имеет большое значение.

В патенте США №6,516,080 (Nur) раскрыт способ выбора REV из репрезентативной области. На Фиг. 2 этого документа показано, как квадратная область, центрированная на одной из сторон образца, увеличивается в размере до тех пор, пока не будет найдена репрезентативная область. Длина стороны квадрата репрезентативной области затем выбирается в качестве длины сторон куба, центрированного в трехмерном образце. Этот способ зависит от того, является ли образец однородным и изотропным. Это не является типичным для многих реальных образцов и пород.

Заявка на патент США №2011/0004447 (Hurley и соавт.) относится к способу характеризации трехмерных пористых сред с применением по меньшей мере одного измерительного инструмента, который получает два или более множеств переданных результатов измерений на двух или более глубинах в образце. В этом способе репрезентативный элементарный объем (REV) пористости оценивается посредством (1) случайного выбора множества неперекрывающихся блоков однородного размера из измеренного или смоделированного образца, (2) построения графика пористости отдельного блока в зависимости от объема соответствующего блока и (3) определение отклонения пористости, измеренного для каждого образца для заданного объема блока. Пористость является средней пористостью по выбранному образцу. Когда отклонение измеренной пористости опускается ниже выбранной пороговой величины, соответствующий объем является REV пористости исследуемой породы. В этом способе Hurley и соавт. объем не растет, начиная с точки, и поэтому будет покрывать больше возможных подобъемов, что фактически уменьшит размер образца. Способ имеет недостатки, заключающиеся в том, что он был разработан для использования множества подобразцов с тем, чтобы можно было получить статистически значимое отклонение и, возможно, причем потребуется использовать большой образец для того, чтобы получить требуемую сходимость; эти две потребности не всегда могут быть удовлетворены, что может привести к выбору всего исходного образца в качестве RV. Изобретатели настоящего изобретения показали, что это происходит в случае образца, подвергнутого лазерной сканирующей конфокальной микроскопии (LSCM). Способ Hurley и соавт. также, возможно, не сможет идентифицировать наименьший возможный REV в образце.

Интересным и мощным подходом для характеризации микроструктуры пористых сред является стохастический анализ теории локальной пористости Hilfer (1992). Этот способ формулируется зависимым от масштаба образом и дает хорошую оценку интегрального масштаба длины для REV. Однако способ локальный пористости не дает результатов относительно анизотропности пористого пространства. Усовершенствование данного способа было выполнено Liu и соавт. (2009 и 2010); причем оценивалось локальное распределение анизотропии зависимым от масштаба образом. Это усовершенствование потребовало применения способа Ketcham (2005), в котором анизотропия является функцией зависящего от направления изменения характера пористых структур.

Множество оценок свойств пористых сред, таких как порода, выполняются с применением закона Дарси. Закон Дарси является феноменологически выведенным уравнением, которое аппроксимирует поток текучей среды через пористую среду. Закон был сформулирован Генри Дарси на основании результатов экспериментов, которые он провел для потока воды через песчаный слой. Закон Дарси по существу является выражением закона сохранения импульса. Закон Дарси, поскольку он часто применяется для потока через пористые среды, такие как образцы породы, может применяться для выполнения оценки объемного потока с помощью уравнения 1, которая имеет параметры потока Дарси в соответствии с проиллюстрированным на фиг. 24:

где

Q = объемная скорость потока в пределах одной фазы образца за единицу времени,

k = абсолютная проницаемость пористой среды,

A = площадь сечения для потока,

µ - динамическая вязкость,

Pb, Pa = давление на входе и выходе из объема,

L = длина образца.

Формально, для выведения закона Дарси для определения проницаемости, например, из первого принципа, должна быть подтверждена некоторая гипотеза. В частности, как показано в работе Whitaker, S., Transport in Porous Media 1, 1986, pp. 3-25, способ выведения закона Дарси из уравнений Навье-Стокса (то есть уравнений для импульса) состоит в том, чтобы применить разложение Гари:

,

которое по существу является разложением шкал: является усредненной величиной (в этом случае давление), которая, как предполагается, «правильно ведет себя» по усредненному интегральной шкале (которая может быть шкалой длины образца, такой как поперечная или продольная размерность). Другими словами, эти усредненные функции, как предполагается, достаточно описывают величины, которые они представляют. Например, сигнал давления, который быстро изменяется по шкале длины сопоставимому с усредненной шкалой длины, не может представлять давление по этой длине. Величина является флуктуирующей частью давления, причем она является вариацией функции. Гипотеза состоит в том, что усредненные величины не изменяются на малых шкалах, где флуктуирующая часть может иметь только небольшое изменение. Для того чтобы вывести закон Дарси вместе с разложением Гари, к уравнениям Навье-Стокса также должна быть применена операция усреднения (например, метод усреднения по объему). Однако в этом случае получают среднее градиентов полей, в то время как требуется градиент усредненных величин (как показано в законе Дарси). Можно легко доказать, что эти два оператора (градиент и усреднение) заменяются, когда применяются к функциям, которые не изменяются быстро по усредненным шкалам длины. В частности, если пористость является однородной, закон Дарси может быть записан в более общем виде как формула 2:

,

где

q (x)^-= усредненная по объему плотность потока в позиции x,

k = абсолютная проницаемость пористой среды в позиции x,

µ = динамическая вязкость,

= Градиент внутреннего (в порах) среднего давления в позиции x.

При использовании данной формулы рассматривается шкала, в которой усредненные значения изменяются в зависимости от позиции, и флуктуирующая часть отсутствует. Эта формула может применяться для моделирования потока в резервуаре.

Когда REV выбирается с помощью любого из средств, описанных выше, имеется возможность того, что может существовать вариация пористости в пределах REV, и это делает предположения о потоке Дарси некорректными и предрасположенными к ошибке. Кроме того, градиент давления может быстро изменяться вдоль направления потока, что делает невозможным определение проницаемости, связанной с конкретной частью образца. Это особенно верно для образцов, обладающих высокой неоднородностью, таких как образцы, которые могут быть обнаружены в реальных горных породах.

Изобретатели настоящего изобретения поняли, что существует потребность в более эффективном способе оценки репрезентативного элементарного объема (REV) в образце пористых сред, включая гетерогенные образцы. Кроме того, анализ должен учитывать направленное изменение строения пор в зависимости от направления, чтобы учесть анизотропию пористых сред и, в случае рассмотрения направленного свойства такого, как поток, учесть направление потока.

Раскрытие изобретения

Признак настоящего изобретения заключается в создании эффективного способа оценки репрезентативного элементарного объема (REV) в образце пористых сред, таких как порода, в котором выбранный подобъем является лучшим приближением элементарного объема по сравнению с существующими способами.

Дополнительный признак настоящего изобретения состоит в создании эффективного способа определения REV в образце пористых сред, таких как порода, в котором REV выбирается в отношении ожидаемого направления потока текучей среды через пористые среды.

Дополнительный признак настоящего изобретения состоит в создании эффективного способа количественного определения того, насколько хорошим (или насколько плохим) является цифровое представление породы и насколько точным будет описание потока текучей среды с помощью закона Дарси.

Дополнительный признак настоящего изобретения состоит в создании способа определения надежного критерия для понимания, когда тенденция проницаемости-пористости нарушается вследствие недостаточного размера подобразца.

Дополнительный признак настоящего изобретения состоит в создании способа анализа пористой структуры зависящим от масштаба образом, включая информацию о направлении изменения неоднородностей.

Чтобы достичь этих и других преимуществ, и в соответствии с задачами настоящего изобретения, как реализовано и в широком смысле описано в настоящем описании, настоящее изобретение относится, в одной своей части, к способу идентификации репрезентативного цифрового объема подобразца, соответствующего образцу пористых сред, который содержит этапы, на которых a) получают сегментированный объем, характеризующий пространство пор и по меньшей мере одну твердую фазу; b) выводят среднее значение <P1> свойства первой целевой функции P1 для всего сегментированного объема; c) вычисляют среднеквадратическое отклонение σ_vol относительно среднего значения <P1> свойства для всего сегментированного объема; d) определяют множество подобъемов в объеме; e) вычисляют среднеквадратическое отклонение σ_i значения свойства P первой целевой функции P1 относительно среднего значения <P1> свойства для каждого из упомянутых подобъемов; f) находят все репрезентативные подобъемы-кандидаты, для которых среднеквадратическое отклонение σ_i удовлетворительно соответствует σ_vol; g) выбирают и сохраняют репрезентативный подобъем из кандидатов; и h) используют репрезентативный подобъем для выведения по меньшей мере одного интересующего значения свойства.

Настоящее изобретение также относится к способу идентификации репрезентативного цифрового объема подобразца, соответствующего образцу пористых сред, который включает в себя этапы, на которых a) получают сегментированный объем, характеризующий пространство пор и по меньшей мере одну твердую фазу; b) ориентируют выбранную ось декартовой системы координат сегментированного объема к определенному направлению потока; c) выводят значения как одной или более функций, по меньшей мере первой целевой функции P1 для всего сегментированного объема посредством анализа цифровых срезов, ортогональных определенному направлению потока; d) определяют множества подобъемов в объеме; e) вычисляют значения для одной или более функций, по меньшей мере первой целевой функции P1 для каждого из упомянутых подобъемов, соответствующих определенному направлению потока; f) находят все репрезентативные подобъемы-кандидаты, для которых функция (-и) идентифицирует(-ют) соответствие между значениями для объема и подобъема; g) выбирают репрезентативный объема из кандидатов; h) сохраняют репрезентативный подобъем; и i) используют репрезентативный подобъем для моделирования или выведения по меньшей мере одного интересующего значения свойства.

Настоящее изобретение также относится к способу получения эффективной оценки репрезентативного элементарного объема по большему цифровому 3-D изображению пористого образца, который содержит этапы, на которых a) получают сегментированный объем, характеризующий пространство пор и по меньшей мере одну твердую фазу; b) выводят значения как по меньшей мере одной функции по меньшей мере первой целевой функции P1 для всего сегментированного объема; c) определяют множество подобъемов в объеме, причем на этом этапе определяют исходный размер для подобъема, заполняют весь объем подобъемами определенного исходного размера, итерируют размеры для последующих подобъемов и заполняют весь объем подобъемами такого размера и повторяют этот этап до тех пор, пока не будет выполнено условие прерывания; d) вычисляют значения как по меньшей мере одной функции по меньшей мере для первой целевой функции для каждого из упомянутых подобъемов; e) находят все репрезентативные -подобъемы-кандидаты для достаточно удовлетворяющих друг другу значений объема и подобъема; f) выбирают и сохраняют репрезентативный подобъем из кандидатов; и g) используют репрезентативный подобъем для проведения моделирования или выведения по меньшей мере одного интересующего значения свойства.

Настоящее изобретение также относится к способу получения эффективной оценки репрезентативного элементарного объема по большему цифровому 3-D изображению пористого образца, который содержит этапы, на которых a) получают сегментированный объем, характеризующего пространство пор и по меньшей мере одну твердую фазу; b) ориентируют выбранную ось декартовой системы координат сегментированного объема к определенному направлению потока; c), выводят среднее значение <P1> свойства первой целевой функции P1 для всего сегментированного объема с применением анализа множества цифровых срезов объема образца, взятых ортогонально к определенному направлению потока; d) вычисляют среднеквадратическое отклонение относительно среднего значения <P1> свойства для всего сегментированного объема; e) определяют множество подобъемов в пределах объема, причем на этом этапе определяют исходный размер для подобъема, заполняют весь объем подобъемами определенного исходного размера, итерируют размеры для дальнейших подобъемов от больших к меньшим и заполняют весь объем подобъемами такого размера и повторяют этот этап до тех пор, пока не будет выполнено условие прерывания; f) вычисляют среднеквадратическое отклонение σ_i свойства P относительно среднего значения <P1> свойства для каждого из упомянутых подобъемов, в отношении определенного направления потока; g) находят все репрезентативные -подобъемы-кандидаты, для которых σ_i удовлетворительно соответствует σ_vol; h) выбирают наименьший кандидат и его сохраняют в качестве репрезентативного элементарного объема; и i) используют репрезентативный элементарный объем для выведения по меньшей мере одного интересующего значения свойства.

Настоящее изобретение также относится к способу идентификации цифрового объема репрезентативного подобразца, соответствующего образцу пористых сред, который содержит этапы, на которых 1) загружают сегментированное трехмерное изображение пористой среды в компьютерную систему, причем сегментированное трехмерное изображение содержит вокселы, каждому из которых присваивается значение по шкале полутонов; 2) выбирают направление потока, которое определяется как направление Z; 3) определяют размеры объемов запроса, причем i) объем запроса является подобразцом исходного сегментированного трехмерного изображения с размерами Xi, Yi и Zi, причем размеры всего образца составляют Xs, Ys, Zs, ii) определяют максимальное число объемов запроса, imax, iii) устанавливают размеры в вокселах для каждого объема запроса (Xi, Yi, Zi), причем Xi, Yi и Zi определяют для значений i от 1 до imax, и iv) начальное значение i устанавливается равным 1; 4) вычисляют выбранные свойства Ps(0,0,0) через Ps (0,0, Zs) для каждого среза объема запроса; 5) вычисляют σ_s (0,0,0); 6) устанавливают максимальные координаты для того, чтобы объем запроса размера Xi, Yi, Zi занимал в пределах всего образца размера Xs, Ys, Zs, причем amax=Xs-Xi+1, bmax=Ys-Yi+1, cmax=Zs-Zi+1; 7) устанавливают координаты положения текущего объема запроса на a=b=c=0; 8) вычисляют выбранные свойства Pi(a, b, c) через Pi (a, b, c+Zi) для срезов текущего объема запроса, причем выбранные свойства содержат пористость, отношение площади поверхности к объему, похожие свойства или произвольную их комбинацию, 9) вычисляют σ_i (a, b, c), причем при необходимости значения Pi, которые используются для вычисления значения σ_i, фильтруются, причем при необходимости устанавливают среднее значение для Pi; 10) перемещают положение объема запроса на 1 воксел в направлении X, a=a+1; 11) повторяют этапы 8)-10) и сохраняют все величины Pi и σi, пока значение X-координаты текущего объема запроса, a, не будет равно максимальному значению, которое может занимать текущий объем запроса, amax; 12) устанавливают координату X текущего объема запроса равной нулю, a = 0, и увеличивают координату Y текущего положения объема на один воксел, b=b+1; 13) повторяют этапы 8) - 12), и сохраняют все величины Pi и σi, пока значение Y-координаты текущего объема запроса, b, не будет равно максимальному значению, которое может занимать текущий объем запроса, bmax; 14) устанавливают координату X текущего объема запроса равной нулю, a=0, устанавливают координату Y текущего объема запроса равной нулю, b=0, и увеличивают координату Z текущего положения объема на один воксел, c=c+1; 15) повторяют этапы 8)-14), и сохраняют всех величин Pi и σi, пока значение Z-координаты текущего объема запроса, c, не будет равно максимальному значению, которое может занимать текущий объем запроса, cmax; 16) увеличивают размер текущего объема запроса, причем на этом этапе i) выбирают следующее множество объемов запроса, посредством увеличения указателя до следующего объема запроса, i=i+1 и ii) устанавливают текущий размер запроса на Xi, Yi, Zi; 17) повторяют этапы 6)-16), пока все объемы запроса не будут выбраны, и все величины Pi и σi не будут вычислены и сохранены; 18) выбирают одно или более выбранных свойств для сопоставления 19) вычисляют λi для каждого объема запроса; 20) выбирают объем запроса с наименьшим значением λi, причем выбранный объем запроса является размером и положением REV; и 21) вычисляют свойства пористой среды.

Также предусмотрены компьютеризированные системы, машиночитаемые носители и программы для выполнения способов.

Следует понимать, что приведенное выше общее описание и приведенное ниже подробное описание являются примерными и поясняющими и предназначены только для обеспечения дальнейшего объяснения настоящего изобретения.

Сопровождающие чертежи, которые входят в состав и являются частью настоящей заявки, иллюстрируют некоторые из вариантов осуществления настоящего изобретения и вместе с описанием служат для объяснения принципов настоящего изобретения. Чертежи не обязательно изображены в масштабе. Аналогичные ссылочные позиции на чертежах относятся к аналогичным элементам на различных видах.

Краткое описание чертежей

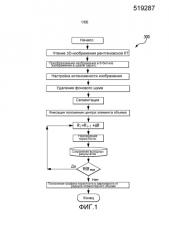
Фиг. 1 - блок-схема, иллюстрирующая практику из уровня техники для идентификации REV с применением программы М-REV.

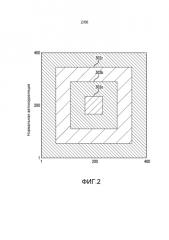
Фиг. 2 иллюстрирует другую схему взятия образцов из уровня техники для идентификации REV с выбором REV из репрезентативной области.

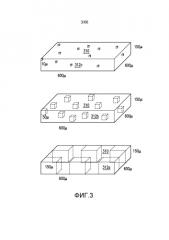
Фиг. 3 иллюстрирует другую схему взятия образцов из уровня техники для идентификации REV с применением способа пористости REV.

Фиг. 4 - график измеренного свойства в зависимости от объема образца, иллюстрирующий предшествующее определение REV.

Фиг. 5A и 5B иллюстрируют выбор подобразца со связностью полостей пор, смоделированной с помощью системы потока текучих сред, состоящей из труб, имеющих большие трубопроводы, соединенные через малые ограничивающие трубопроводы, в соответствии с примером из настоящей заявки.

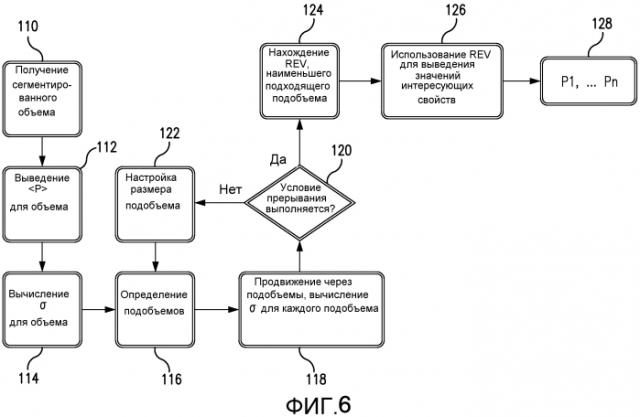
Фиг. 6 иллюстрирует блок-схему способа оценки REV, основанного на статистической квалификации подобъемов в соответствии с примером из настоящей заявки.

Фиг. 7 иллюстрирует репрезентативной объем и объем запроса, которые включают в себя определение терминов, относящихся к образцу и объему запроса, в соответствии с примером из настоящей заявки.

Фиг. 8A и 8B иллюстрируют выбор подобъема в смоделированной системе потока текучей среды, имеющей явные характеристики направления потока текучей среды в соответствии с примером из настоящей заявки, причем фиг. 8A является видом сверху трубопроводов потока текучей среды, и фиг. 8B является сечением трубопроводов потока текучей среды, выполненное вдоль линии 8B-8B фиг. 8A.

Фиг. 9 иллюстрирует цифровой срез объема запроса в соответствии с примером из настоящей заявки.

Фиг. 10 - блок-схема, иллюстрирующая способ оценки REV, дополнительно включающий в себя ориентирование сетки в соответствии с потоком, тестирование пригодности подобъема относительно множества свойств, и систематического перемещения через подобъемы в соответствии с примером из настоящей заявки.

Фиг. 11A и 11B иллюстрируют выбор подобъема в более сложной смоделированной системе потока текучей среды в соответствии с примером из настоящей заявки, в котором декартова система координат перестраивается на фиг. 11A, и фиг. 11B является сечением, полученным на линии 11B-11B на фиг. 11A.

Фиг. 12 иллюстрирует сегментированный объем, представляющий образец естественной породы, имеющий по существу гетерогенные признаки в соответствии с примером из настоящей заявки.

Фиг. 13 иллюстрирует сегментированный объем, представляющий образец естественной породы, имеющий менее разнородную структуру, чем образец, проиллюстрированный на фиг. 12, в соответствии с примером из настоящей заявки.

Фиг. 14 - подробная блок-схема, описывающая один из вариантов осуществления в соответствии с примером из настоящей заявки.

Фиг. 15A и 15B иллюстрируют распределения среднеквадратическое отклонение для отношения поверхности/объема и пористости, соответственно, для системы потока текучей среды, смоделированной на фиг. 11A и 11B, причем размер объема запроса соответствует элементарной ячейке, которая соответствует периодичности в пределах всего образца в соответствии с примером из настоящей заявки.

Фиг. 16A-16E иллюстрируют среднеквадратическое отклонение пористости в системе потока текучей среды для различных размеров объема запроса в системе потока текучей среды, смоделированной на фиг. 11A-11B, в соответствии с примером из настоящей заявки.

Фиг. 17A-17E иллюстрируют среднеквадратическое отклонение отношения поверхности к объему для пространства пор в системе потока текучей среды для различных размеров объема запроса в системе потока текучей среды, смоделированной на фиг. 11A-11B в соответствии с примером из настоящей заявки.

Фиг. 18A-18B иллюстрируют среднеквадратическое отклонение для целевых функций пористости (фиг. 18A) и отношения поверхности к объему (фиг. 18B) для образца породы фиг. 13 для объема запроса 450×450×450, в соответствии с примером из настоящей заявки.

Фиг. 19A-19B иллюстрируют среднеквадратическое отклонение для целевых функций пористости (фиг. 19A) и отношения поверхности к объему (фиг. 19B) для образца породы фиг. 13 для объема запроса 300×300×300, в соответствии с примером из настоящей заявки.

Фиг. 20A-20B иллюстрируют среднеквадратическое отклонение для целевых функций пористости (фиг. 20A) и отношения поверхности к объему (фиг. 20B) для образца породы с фиг. 13 для объема запроса 200×200×200, в соответствии с примером из настоящей заявки.

Фиг. 21A-21B иллюстрируют среднеквадратическое отклонение для целевых функций пористости (фиг. 21A) и отношения поверхности к объему (фиг. 21B) для образца породы с фиг. 12 для объема запроса 450×450×450, в соответствии с примером из настоящей заявки.

Фиг. 22A-22B иллюстрируют среднеквадратическое отклонение для целевых функций пористости (фиг. 22A) и отношения поверхности к объему (фиг. 22B) для образца породы с фиг. 12 для объема запроса 300×300×300, в соответствии с примером из настоящей заявки.

Фиг. 23A-23B иллюстрируют среднеквадратическое отклонение для целевых функций пористости (фиг. 23A) и отношения поверхности к объему (фиг. 23B) для образца породы с фиг. 12 для объема запроса 200×200×200, в соответствии с примером из настоящей заявки.

Фиг. 24 - схематическая иллюстрация потока Дарси.

Фиг. 25 иллюстрирует три тенденции пористости-проницаемости на графике абсолютной проницаемости (мД) в зависимости от пористости (как дробную величину между 0 и 1,0) для образца породы Фонтенбло для размерности подобразца 95×95×95 (серые треугольники), 190×190×190 (серые круги) и 285×285×285 (серые кресты), и который содержит значение пористости-проницаемости для исходного размера образца 500×500×500 для линии тенденции (сплошная серая линия "UL", которая включает в себя точку данных в виде полого ромба), и черные символы являются оптимальными выборами, сделанными при использовании в качестве целевых значений и функции поверхности/объема и пористости в соответствии с примером из настоящей заявки. Эти две линии являются нижними и верхними пределами, соответственно, которые получены из экспериментов, сделанных для этих породах.

Фиг. 26 иллюстрирует тенденции корреляции пористости/проницаемости (poro-perm) на графике абсолютной проницаемости (мД) в зависимости от пористости для образца неуплотненного песчаника для размерностей подобразца 300×300×300 (серые кресты), 200×200×200 (серые круги) и 100×100×100 (серые треугольники), в соответствии с примером из настоящей заявки. Два набора данных, то есть «1_100» и «1_200», и также «2_100» и «2_200», представлены для двух различных образцов (образцов 1 и 2). Два образца очень похожи.

Фиг. 27 иллюстрирует кривые тенденции пористости-проницаемости на графике абсолютной проницаемости (мД) в зависимости от пористости для образца Фонтенбло более низкой пористости, чем образец с фиг. 25, который содержит тенденции пористости-проницаемости для размерности подобразца 190×190×190 (серые треугольники), 285×285×285 (серые круги) и 380×380×380 (серые кресты), и который включает значение пористости-проницаемости для исходного размера образца 500×500×500 для линии тенденции UL (сплошная серая линия, которая пересекает символ в виде полого ромба, и черные символы представляют оптимальный выбор, сделанный при использовании в качестве целевых значений и функции поверхности/объема, и пористости, в соответствии с примером из настоящей заявки. Кривая «нижнего лабораторного значения» является нижним пределом из экспериментов, сделанных для этих пород.

Фиг. 28A-28H иллюстрируют среднее значение отношения (A) распределения среднеквадратическое отклонение для пористости (фиг. 28A), отношения поверхности к объему (фиг. 28B), дисперсию (V) того же самого распределения для пористости (фиг. 28C), дисперсию отношения поверхности к объему (фиг. 28D), асимметрию для пористости (фиг. 28E), дисперсию асимметрии (фиг. 28F), эксцесс для пористости (фиг. 28G) и дисперсию эксцесса (фиг. 28H) - все в зависимости от размерности (размера) подобъема образца для двух различных пород Фонтенбло, рассматриваемых на фиг. 25 и фиг. 27 соответственно в соответствии с примером из настоящей заявки. Порода Фонтенбло, рассматриваемая на фиг. 25, представлена на фиг. 28A-28H кривыми, которые определены черными кругами, и порода, рассматриваемая на фиг. 27, представлена кривыми, определенными на фиг. 28A-28H серыми кругами. На фиг. 28A-28H графики пронумерованы в соответствии с номерами, приведенными во вставленных легендах и на фиг. 25 и 27.

Фиг. 29A-29H иллюстрируют среднюю величину отношения (A) распределения среднеквадратическое отклонение для пористости (фиг. 29A), отношения поверхности к объему (фиг. 29B), дисперсию (V) того же самого распределения для пористости (фиг. 29C), дисперсию отношения поверхности к объему (фиг. 29D), асимметрию для пористости (фиг. 29E), дисперсию асимметрии (фиг. 29F), эксцесс для пористости (фиг. 29G) и дисперсию эксцесса (фиг. 29H) - все в зависимости от размерности (размера) подобъема образца, для двух различных карбонатных пород, соответственно, причем один образец показан серыми кругами, и другой образец показан черными кругами на этих графиках, в соответствии с примером из настоящей заявки. На фиг. 29A-29H графики пронумерованы в соответствии с номерами, приведенными во вставленных легендах и на фиг. 29I и 29J.

Фиг. 29I-29J иллюстрируют тенденции пористости-проницаемости для двух различных карбонатных пород, рассматриваемых на фиг. 29A-29H, в соответствии с примером из настоящей заявки. Фиг. 29I содержит тенденции пористости-проницаемости для образца, идентифицированного серыми кругами на фиг. 29A-29H для размерностей подобразца 95×95×95, 190×190×190 и 285×285×285, и который включает в себя значение пористости-проницаемости для исходного измерения (размера) образца 500×500×500 для линии тенденции D1 (сплошная серая линия, символ полого ромба), и черные символы представляют оптимальный выбор, сделанный при использовании в качестве целевых значений и функции поверхности/объема, и пористости. Фиг. 29J содержит тенденции пористости-проницаемости для образца, идентифицированного черными кругами на фиг. 29A-29H для размерностей подобразца 190×190×190, 285×285×285 и 380×380×380, и который включает значение пористости-проницаемости для объема исходного образца 500×500×500 для линии тенденции D2 (сплошная серая линия, символ полого ромба), и черные символы являются оптимальным выбором, сделанным при использовании в качестве целевых значений и функции поверхности/объема, и пористости.

Фиг. 30A-30I иллюстрируют среднее значение отношения (A) распределения среднеквадратическое отклонение для пористости (фиг. 30A), отношения поверхности к объему (Фиг. 30B), дисперсию (V) того же самого распределения для пористости (фиг. 30C), дисперсию отношения поверхности к объему (фиг. 30D), асимметрию для пористости (фиг. 30E), дисперсию асимметрии (фиг. 30F), эксцесс для пористости (фиг. 30G) и дисперсию эксцесса (фиг. 30H) - все в зависимости от размерности (размера) подобъема образца для двух различных относительно однородных пород, соответственно, с одним образцом, показанным серыми кругами, и другим образцом, показанным черными кругами на этих графиках, в соответствии с примером из настоящей заявки. На фиг. 30A-30I, графики пронумерованы в соответствии с номерами, приведенными в условных обозначениях во вставленных легендах. Как и на предыдущих чертежах, на этих чертежах показаны графики для двух различных однородных образцов породы.

Фиг. 31A-31I иллюстрируют среднюю величину отношения (A) распределения среднеквадратическое отклонение для пористости (фиг. 31A), отношения поверхности к объему (фиг. 31B), дисперсию (V) того же самого распределения для пористости (фиг. 31C), дисперсию отношения поверхности к объему (фиг. 31D), асимметрию для пористости (фиг. 31E), дисперсию асимметрии (фиг. 31F), эксцесс для пористости (фиг. 31G) и дисперсию эксцесса (фиг. 31H) - все в зависимости от размерности (размера) подобъема образца для двух дополнительных пород, соответственно, с одним образцом, показанным серыми кругами, и другим образцом, показанным черными кругами на этих графиках, в соответствии с примером из настоящей заявки. На фиг. 31A-31I графики пронумерованы в соответствии с номерами, приведенными в условных обозначениях во вставленных легендах и на фиг. 31I и 31J. Породы, используемые в качестве образцов, являлись песчаниками (Фонтенбло).

Фиг. 31I-31J иллюстрируют тенденции пористости-проницаемости для двух различных пород, рассматриваемых на фиг. 31A-31I, в соответствии с примером из настоящей заявки. Фиг. 31I включает в себя тенденции пористости-проницаемости для образца, идентифицированного серыми кругами на фиг. 31A-31I для размерностей подобразца 190×190×190, 285×285×285 и 380×380×380 и который включает в себя значение пористости-проницаемости для исходного размера измерения образца 500×500×500 для линии тенденции D3 (сплошная серая линия, символ полого ромба), и черные символы являются оптимальным выбором, сделанным при использовании в качестве целевых значений и функции поверхности/объема, и пористости. Фиг. 31J включает в себя тенденции пористости-проницаемости для образца, идентифицированного черными кругами на фиг. 31A-31I, для размерностей подобразца 95×95×95, 190×190×190 и 285×285×285 и который включает значение пористости-проницаемости для объема исходного образца 500×500×500 для линии тенденции D4 (сплошная серая линия, символ полого ромба), и черные символы являются оптимальным выбором, сделанным при использовании в качестве цел