Эффективный способ определения режимных значений случайных геофизических величин

Эффективный способ определения режимных значений случайных геофизических величин

Иллюстрации

Показать все

Реферат

Область техники

Предлагаемое изобретение относится к методам определения экстремальных значений по измеренным временным рядам геофизических параметров окружающей среды (например, ветер, волны, течения, температура, давление и т.д.), которые могут наблюдаться (появляться) в заданной географической точке один раз в заданное число лет, например в 10, 30, 50 и 100 лет. Такие величины называются режимными, а вероятности повторения один раз в 30, 50 или 100 лет - режимами [1].

Все виды указанных режимных значений широко используются на практике при оценках риска индустриальной деятельности человека. В частности, в научной и прикладной литературе имеется большое число справочников, атласов и пособий, в которых представлены режимные характеристики волн и ветра для различных акваторий [2, 3]. Полученные результаты широко применяются для решения большого числа практических задач: береговое строительство, безопасность судоходства, морская индустрия нефти и газа, экология, курортное дело и т.п.

Далее все вопросы режимных значений обсуждаются на примере величин скорости ветра и высот волнения, хотя сам предлагаемый способ распространяется на любые случайные геофизические ряды, полученные в результате наблюдений.

Уровень техники

В основе определения режимных значений геофизических величин W используются их долговременные ряды W(t), полученные путем измерений. Здесь t означает набор моментов времени. Сами ряды могут иметь различное происхождение: либо как результаты измерения, либо как результаты моделирования, выполненного при помощи надежных и верифицированных гидродинамических моделей. Для способа определения режимных значений такие ряды считаются эквивалентными и взятыми из измерений (т.е. эмпирическими).

Существует множество подходов к определению режимных значений в заданной географической точке. Главные из этих методов подробно описаны в литературе [1] на примере рядов ветра и высот волн. В основе всех этих методов, как правило, лежат три процедуры (пояснения формул приведены ниже):

1) построение дискретной гистограммы H(W_i) измеренного ряда случайных величин W и построение соответствующей дискретной эмпирической функции обеспеченности F(W_i), выполняемое по известной процедуре;

2) построение аналитической аппроксимации F_ap(W) эмпирической функции обеспеченности F(W_i), которое выполняется в каждом применяемом способе по-разному;

3) выполнение экстраполяции аналитической функции обеспеченности F_ap(W) за пределы максимального значения ряда данных W_M до уровня заданного режима.

Приведем пояснения.

Во-первых, дискретные функции H(W_i) и F(W_i) являются безразмерными, а размерность переменной W определяется ее физическим содержанием и далее не существенна.

Второе. Для гистограммы H(W_i) формулы нет, ее строят в графическом виде. Она строится по ряду измеренной случайной величины W(t) путем подсчета числа попаданий значений величины W в интервал W_i<W≤W_i+ΔW для заданного шага дискретности ΔW и фиксированного набора значений рассматриваемой величины W_i=i*ΔW. Математически, отношение H(W_i)/ΔW соответствует плотности вероятности P(W) для случайной величины W[1], поэтому гистограмма H(W_i) представляет собой эмпирическое представление плотности вероятности P(W) для измеренной случайной величины.

Плотность вероятности P(W) однозначно определяет эмпирическую интегральную функцию обеспеченности измеренного ряда F(W₀), которая задает вероятность того, что случайная величина W может достигать значения W₀. Функция F(W) определяется через функцию плотности вероятности P(W) или гистограмму H(W_i) при помощи соотношений

где W_M есть измеренное максимальное значение ряда. В соотношении (1) знак означает приближенное равенство, достигаемое при малых ΔW и больших W_M. Величины H(W_i) и F(W) не имеют размерности, и поэтому формула (1) применима для любых измеряемых величин (ветер, волны, температура, давление и т.п.).

Третье. Все построения обычно делаются в виде графиков. Примеры построения гистограмм H(W_i) и функций обеспеченности F(W) для скорости ветра приведены на Фиг. 1а, б. Эти кривые построены по рядам измерений на буях, расположенных в Индийском океане [4]. Номера буев указаны на рисунках.

Эмпирическая, т.е. полученная из измерений, функция F(W) (Фиг. 1б) используется для определения режимных значений случайных величин путем ее экстраполяции за пределы максимальной измеренной скорости ветра W_M до уровня заданного режима.

Экстраполяция функции F(W) нужна для определения режимного значения случайной величины W, поскольку для заданного режима оно выходит за пределы максимального измеренного значения W_M. Так, на Фиг. 1а максимальное в ряду значение силы ветра составляет 16 м/с, а вероятность его появления, согласно Фиг. 1б, имеет порядок (2-3)10^-3. Для получения режимного значения скорости ветра, появляющегося один раз в 30 лет, т.е. в режиме один раз в 30 лет, следует оценить соответствующую обеспеченность данного режима. Например, при дискретности наблюдения 8 раз в сутки, искомая вероятность (режим) равна величине F(W)=1/(365*8*30)=1,14·10^-5. Экстраполируя эмпирическую функцию F(W) до уровня режима 1,14·10^-5, согласно Фиг. 1б, получим, что режимное значение скорости ветра, возможное один раз в 30 лет, приблизительно равно 25 м/с.

Основная проблема в оценке режимных характеристик заключается в обеспечении требования однозначности и достоверности выполняемой экстраполяции функции F. Ясно, что неточность в экстраполяции приводит к неточности режимной оценки.

Как правило, решение проблемы экстраполяции функции распределения превращается в отдельное самостоятельное исследование (см. описание методов в [1, 5]). Например, для статистического оценивания экстремальных величин, возможных 1 раз в N лет, в способе BOULVAR [1] используется целая система стохастических моделей. На этой основе созданы справочники нового поколения по ветру и волновому климату [2].

Все другие способы требуют иных, но столь же сложных и неоднозначных действий [5]. Неоднозначность обусловлена практической необходимостью всегда строить гипотезы о том, какой интегральной совокупностью факторов должна определяться экстремальность геофизического процесса. Именно эти гипотезы снижают степень достоверности полученных значений. В итоге, как указано в [1, 5], явно приоритетных способов экстраполяции эмпирической функции обеспеченности F(W) пока не установлено. Физически это объясняется тем, что геофизические величины, как правило, подвержены многомасштабной изменчивости, а универсальное распределение, единым образом ее описывающее, в природе может и не существовать.

Из сказанного следует, что проведение упомянутых режимных исследований весьма затруднительно и требует большого времени. Поэтому необходимы иные, более эффективные, т.е. более быстрые, но достаточно точные способы построения достоверных экстраполяций эмпирических функций обеспеченности F(W), которые статистически соответствуют данным измерений.

В данной заявке предлагается новый эффективный способ, повышающий достоверность получаемых оценок режимных величин.

Раскрытие изобретения

Для достижения искомого технического результата - повышения эффективности определения режимных значений геофизических величин, заданных данными измерений, в предлагаемом способе нами учитываются следующие обстоятельства, которые требуют выполнения новых технологических действий.

1. Поскольку значения функции F(W), полученной по данным измерений, крайне малы по величине, то аппроксимацию F_ap(W) и ее дальнейшую экстраполяцию проводят в логарифмических координатах для F(W), сохраняя линейные координаты по переменной W. Такой прием повышает точность аппроксимации именно малых величин.

2. Нами установлено, что для выполнения последующей экстраполяции F_ap(W) эмпирической функции обеспеченности F(W), главную роль играют только малое число N (не более 10) последних значений эмпирической функции F(W), т.е. малая область вблизи максимального измеренного значения ряда W_M. Такая область, называемая далее областью построения аппроксимации F_ap(W), обозначается символом [W_lo, W_hi] и задается выражением

где W_lo есть нижняя, a W_hi - верхняя границы области построения аппроксимации.

3. С целью повышения точности, аналитическую аппроксимацию логарифма эмпирической функции ln{F(W)} (см. п. 1 выше), в области построения [W_lo, W_hi], следует выполнять путем представления логарифма искомой функции аппроксимации ln{F_ap(W)} в виде полинома степени n, т.е. в виде

а его коэффициенты А₀, A₁, …, A_n, определять любым известным методом (например, методом наименьших квадратов), встроенным в стандартное обеспечение компьютера (например, пакет программ EXEL). При этом надо использовать только те полиномы, которые монотонно спадают по величине, и для которых выполняется условие

где N - число дискретных точек функции F(W) в области построения аппроксимации (2).

При таком способе построения аппроксимации F_ap(W) (и ее экстраполяции) достигаются, как высокая точность F_ap(W), так и простота ее получения, что и представляет техническое преимущество перед имеющимися аналогами (см. раздел «уровень техники»). Это преимущество, обеспечивающее повышение эффективности определения режимных величин (точность, быстрота, надежность), составляет основной технический результат предлагаемого способа.

4. Для обеспечения наибольшей достоверности аппроксимации F_ap(W), параметры ее построения: n, W_lo и W_hi подбирают так, чтобы значение аппроксимации F_ap(W_M) в точке максимальной величины данных измерений W=W_M превышало значение исходной, «эмпирической» функции F(W_M), полученной по данным измерений. Это важное новое техническое требование. Оно обусловлено тем, что при измерениях нет гарантий замера именно максимального значения измеряемой случайной переменной, в силу временной дискретности наблюдений. Но, на указанное выше превышение накладывают условие нахождения аппроксимации F_ap(W) в пределах эмпирической точности измерений вида

где Δ - эмпирическая погрешность величины ln{F(W_M)}, которую определяют по данным измерений. Именно условие (5) обеспечивает повышение достоверности определения вида F_ap(W) и, как следствие, точности режимных величин для заданного измеренного ряда.

Нами установлено, что в координатах натурального логарифма, т.е. для величины ln{F(W_M)}, максимальное значение погрешности есть Δ=ln(2)≈0.7. В реальных измерения она может быть и меньше, что требует ее определения. На данном этапе разработки метода, при использовании условия (5) следует брать указанную величину Δ.

5. Для обеспечения оптимального выбора аппроксимации F_ap(W), проводят ее оптимизацию путем варьирования параметров n, W_lo и W_hi, т.е. выбирают вариант с минимальной среднеквадратичной ошибкой отклонения δ функции F_ap(W) от исходной эмпирической функции F(W) в области W_lo≤W≤W_hi. Величину 6 рассчитывают по известной формуле

В (6) первый сомножитель под корнем есть обратное число N используемых точек в области построения аппроксимации [W_lo, W_M], a F_ap(W; n) означает, что аппроксимация задается полиномом порядка n.

Возможность реализации

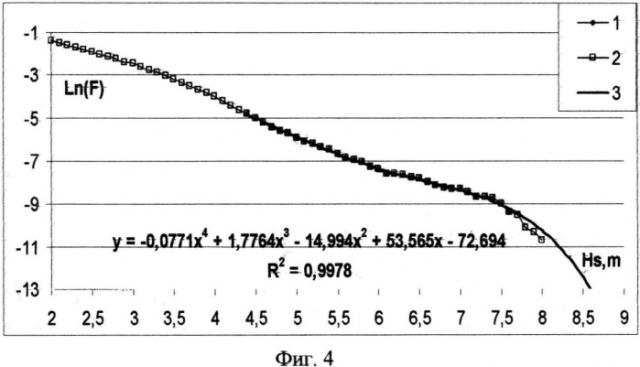
Пример реализации предлагаемого способа определения режимных характеристик приводится на Фиг. 2-4. Все приводимые результаты получены с применением широко распространенного пакета программ EXEL Microsoft office.

Так, например, на Фиг. 2а приведены результаты построения гистограммы Н (обозначенной Hysto) и функции обеспеченности F (обозначенной Prov) для эмпирического 30-летнего ряда высот волнения H_s(t) в центральной точке Аравийского моря (Индийский океан), а на Фиг. 2б дана аналитическая аппроксимация «хвоста» F(H_s) по предлагаемому способу (уравнение аппроксимации приведено на фигуре). Наличие двух максимумов на гистограмме Фиг. 2а явно указывает на то, что для построения аппроксимации F(H_s) пригодны только значения эмпирической функции обеспеченности F(H_s), для которых высота волн H_s>4 м, что и показано на Фиг. 2б.

Как видно из Фиг. 2б, уже для полинома 2-й степени наблюдается прекрасное совпадение аппроксимации F_ap(H_s) с эмпирической функцией F(H_s) в области построения аппроксимации с высокой величиной статистической достоверностью аппроксимации: R²=0.9994. Ее экстраполяция (линия 3) за пределы измеренных максимальных волн H_sR=7,3 м, дает возможность определять любые режимные значения. Например, режиму 1 раз в 100 лет соответствует режимное значение H_sR100 = 7,8 м.

Для той же гистограммы, использование полинома 4-й степени (Фиг. 3) оказывается неприемлемым, в силу невыполнения условия (5). Но, например, уже для центральной точки в Бенгальском заливе (Индийский океан) (Фиг. 4), более точной является именно аппроксимация F(H_s) полиномом 4-й степени (режимное значение H_sR100 = 8,6 м).

Таким образом, реализация метода действительно демонстрирует простоту, надежность, и возможность получения искомых величин с высокой достоверностью.

Источники информации

1. Лопатухин Л.И. Ветровое волнение: Учеб. пособие. 2-е изд. СПб.: ВВМ. - 2012. - 165 с.

2. Справочные данные по режиму ветра и волнения Берингова и Белого морей. / Ред. Лопатухин Л.И., Бухановский А.В., Чернышева Е.С. / Российский Морской Регистр Судоходства. - 2010. - 565 с.

3. Coastal Engineering manual for Coastal Engineering, US Army Corps of Engineers (CEMCE), 2003. http://publications.usace.army.mil/publications/eng-manuals.

4. Polnikov V.G, Pogarskii F.A. Short-Term Variability of Wind and Waves, Based on Buoy Measurements and Numerical Simulations in the Hindustan Area // Marine Science. - 2013. - №3. - P. 48-53.

5. Caires S., Sterl A. 100-Year Return Value Estimates for Ocean Wind Speed and Significant Wave Height from the ERA-40 Data // J. Climate. - 2005. - V. 18, #4. - P. 1032-1048.

1. Способ определения режимных значений геофизической величины W - скорости ветра, высоты волнения, температуры воздуха, в котором геофизическую величину W многократно измеряют, по результатам измерений формируют временной ряд данных W(t) и, с использованием ряда данных измерений W(t), строят эмпирическую вероятностную функцию обеспеченности F(W), затем для нее определяют аналитическую аппроксимацию функции обеспеченности F_ap(W), которую экстраполируют за пределы максимального значения данных измерений W_M до значения заданного вероятностного режима, по которому определяют искомое режимное значение геофизической величины, отличающийся тем, что аналитическую аппроксимацию F_ap(W) выполняют в виде полинома степени n, коэффициенты которого определяют известным способом в логарифмических координатах для функций обеспеченности и в линейных координатах для геофизической величины W, а нижнюю W_lo и верхнюю W_hi границы области построения аппроксимации [W_lo, W_hi] и степень полинома n подбирают такими, чтобы значение логарифма аппроксимирующей функции F_ap(W_M), взятой в точке максимального значения данных измерений W_M, было больше соответствующего значения эмпирической функции F(W_M) на величину, не превышающую погрешности Δ для F(W_M), которую определяют по данным измерений.

2. Способ по п. 1, отличающийся тем, что при построении аппроксимации функции обеспеченности F_ap(W), границы области построения аппроксимации W_lo и W_hi и порядок полинома n несколько раз изменяют и выбирают из этой серии проб тот вариант аппроксимации, для которого среднеквадратичное отклонение аппроксимирующей функции F_ap(W) от эмпирической функции обеспеченности F(W) является минимальным в области построения аппроксимации [W_lo, W_hi].