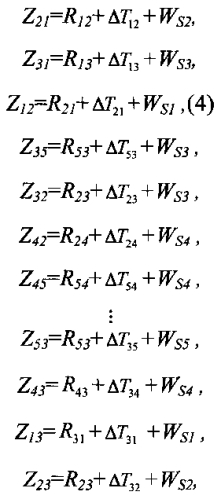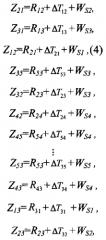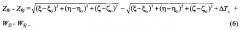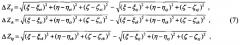Способ идентификации параметров навигационных спутников

Способ идентификации параметров навигационных спутников

Иллюстрации

Показать все

Реферат

Изобретение относится к способам навигации по Спутниковым Радионавигационным Системам (СРНС) и может быть использовано для идентификации параметров навигационных спутников и повышения точности определения координат навигационного приемника. Технический результат заключается в повышении точности определения координат навигационного приемника за счет исключения ошибок взаимной синхронизации часов навигационных спутников и навигационного приемника.

Известны различные способы повышения точности определения координат навигационного приемника. В патенте США №7535414 изложен способ, который предполагает, что перед вычислением координат навигационного приемника производится разрешение неопределенностей, вызванных в т.ч. ошибками часов навигационных спутников, в неполных псевдодальностях. В патенте США № 6417801 предлагается разрешение неопределенностей в неполных псевдодальностях путем добавления в вектор оцениваемых параметров поправки ко времени измерения с последующим перебором всех допустимых целочисленных комбинаций неоднозначностей и выбором нужной из них по критерию минимума остаточных невязок.

Также для повышения точности определения координат навигационного приемника используются различные алгоритмы компенсации погрешностей часов [Интерфейсный контрольный документ ГЛОНАСС (5.1 редакция). - М.: РНИИ КП, 2008. - 57 с.], а также применяется дифференциальный режим измерений по кодовым дальностям, реализуемый с помощью контрольного навигационного приемника с известными географическими координатами - т.н. базовой станции [Bar-Sever, Y. Anew Massachusetts model for GPS yaw attitude // Journal of Geodesy, 70, 714723, 1996]. Недостатками данных способов являются сложность их реализации и невозможность точного определения текущих значений ошибок взаимной синхронизации часов навигационных спутников и навигационного приемника для их последующей компенсации.

Наиболее близким к предлагаемому изобретению является способ, описанный в патенте РФ №2432584. Способ определения координат навигационного приемника спутниковой радионавигационной системы / Васильев М.В., Михайлов Н.В., Поспелов С.С., Джалали Биджан, состоящий в том, что вычисление поправок к координатам приемника производится после измерения псевдодальностей и псевдоскоростей по невязкам псевдодальностей.

Недостатком данного способа также является сложность аппаратной и вычислительной реализации и невозможность точного определения текущих значений ошибок взаимной синхронизации часов навигационных спутников и навигационного приемника для их последующей компенсации.

Заявленное изобретение направлено на решение задачи повышения точности определения местоположения навигационного приемника за счет коррекции погрешности взаимной синхронизации часов навигационных спутников и навигационного приемника.

Поставленная задача возникает при разработке систем контроля и управления навигационными спутниками, а также использования их измерений для решения навигационной задачи объекта.

Для обеспечения идентификации параметров навигационных спутников и упрощения аппаратной и вычислительной реализации данной процедуры предлагается способ, состоящий в том, что в группе из пяти навигационных спутников, находящихся в зоне прямой видимости, реализуются одновременные передача навигационных сообщений от каждого спутника к каждому и их прием каждым спутником от каждого, определение межспутниковых псевдодальностей и их передача на другой спутник с последующим решением на каждом спутнике системы девятнадцати линейных алгебраических уравнений, в результате которого определяются истинные дальности между спутниками, погрешности взаимной синхронизации часов спутников и инструментальные погрешности передатчиков, после чего погрешности взаимной синхронизации часов спутников и инструментальные погрешности передатчиков передаются в навигационных сообщениях и компенсируются в навигационном приемнике при определении координат навигационного приемника на основе решения системы трех нелинейных уравнений, каждое из которых сформировано по разности измеренных псевдодальностей между двумя спутниками.

Точность решения навигационной задачи с использованием средств спутниковой навигации в значительной мере зависит от степени подавления помех, возникающих при приеме-передаче спутниковых сообщений. В общем случае информационная структура спутникового измерения псевдодальности Z_R, используемого в качестве основного сигнала при позиционировании объектов, с учетом помех, в наибольшей степени влияющих на точность позиционирования, имеет вид:

где ξ_с, η_с, ζ_с - текущие координаты спутника в гринвичской системе координат (ГрСК),

ξ, η, ζ - текущие координаты объекта в ГрСК,

C - номинальное значение скорости света в вакууме,

Δτ - погрешность часов навигационного приемника,

ΔT - погрешность часов спутника,

W_ИТ - погрешности, обусловленные прохождением радиосигнала через ионосферу и тропосферу,

W_S - инструментальные погрешности передатчика спутника.

Среди перечисленных погрешностей наиболее значительный удельный вес имеют инструментальные погрешности передатчика спутника и ошибки часов спутника и приемника. Так, например, несмотря на установку атомных часов на навигационных спутниках, среднеквадратическое значение ошибки взаимной синхронизации бортовых шкал времени может достигать 20 и более нс [ГЛОНАСС. Интерфейсный контрольный документ / Навигационный радиосигнал в диапазонах L1, L2 с открытым доступом и частотным разделением (Редакция 5.1). 2008. - 74 с.].

В настоящее время для компенсации погрешности часов применяются различные алгоритмы, построенные на основе ее аппроксимации временными полиномами. Например, в СНС ГЛОНАСС ошибка часов спутника ΔT аппроксимируется линейной зависимостью от времени с заданными параметрами (в GPS применяется квадратичная зависимость):

где t^* - время расчета погрешности на момент поступления спутниковой информации, α₀, α₁ - известные параметры модели ошибки часов спутника, T_Г - время задержки спутникового сигнала, T_Р - релятивистская поправка, определяемая в процессе вычисления координат спутника. Как видно из (2), компенсационная модель содержит 4(!) параметра, требующих дополнительного непростого их определения с различной периодичностью, снижающего общую эффективность применения модели (2). При этом алгоритмы компенсации инструментальных погрешностей передатчика спутника в настоящее время вообще отсутствуют.

Существующие навигационные системы ГЛОНАСС и GPS с целью повышения точности решения навигационной задачи проходят в настоящий момент усиленную модернизацию, позволяющую, в частности, определять с помощью бортовых измерительных средств расстояния между спутниками, находящимися в зоне прямой видимости.

Так, например, навигационные спутники ГЛОНАСС-М оснащаются бортовой аппаратурой межспутниковых измерений [ГЛОНАСС. Принципы построения и функционирования / Под ред. А.И. Перова, В.Н. Харисова. - 3-е изд., перераб. - М.: Радиотехника, 2005. - 688 с.], а навигационные спутники ГЛОНАСС-К - приемоформирующим устройством межспутниковой радиолинии [Ступак Г.Г., Ревнивых С.Г., Игнатович Е.И., Куршин В.В., Бетанов В.В., Панов С.С., Бондарев Н.З., Чеботарев В.Е., Решетнева М.Ф., Балашова Н.Н., Сердюков А.И., Синцова Л.Н. // Выбор структуры орбитальной группировки перспективной системы ГЛОНАС // Космонавтика №3-4 (6) 2013, С. 4-11]. Формирующая часть устройства межспутниковой радиолинии осуществляет формирование и излучение информационно-измерительных радиосигналов, структура которых аналогична структуре навигационного сигнала ГЛОНАСС. В приемной части осуществляется усиление радиосигналов и измерение псевдоскорости и псевдодальности между навигационными спутниками системы ГЛОНАСС.

Повышение точности определения положения навигационных спутников возможно также при использовании лазерных дальномеров [Чубыкин А.А., Рой Ю.А., Корнишев О.М., Падун П.П. Использование бортовых лазерных измерительно-связных средств для повышения точности и оперативности ЭВО спутников системы ГЛОНАСС // ЭВ & ЭС. Т. 12. 2007. С. 25-30, Шаргородский В.Д., Чубыкин А.А., Сумерин В.В. Межспутниковая лазерная навигационно-связная система // Аэрокосмический курьер. 2007. №1 (49). С. 88-89], в основе которого лежит принцип измерения времени распространения лазерных импульсов.

При этом очевидно, что сигналы измерения псевдодальностей между i-м и j-м спутниками будут свободны от погрешностей, обусловленных прохождением сигнала через ионосферу и тропосферу как в (1), и будут иметь вид:

где Z_ij - псевдодальность, измеренная на j-м спутнике,

R_ij - истинная дальность между i-м и j-м спутниками,

ΔT_j - погрешность часов j-го спутника,

ΔT_i - погрешность часов i-го спутника,

W_Si - погрешность передатчика i-го спутника,

ΔT_ji=c(ΔT_j-ΔT_i) - ошибка взаимной синхронизации часов i-го и j-го спутников.

Перед построением алгоритма идентификации искомых пространственно-временных параметров спутников предварительно определим число спутников N, необходимое и достаточное для их полной идентификации. Число всех возможных расстояний между N спутниками (равное числу ребер графа с N вершинами) определяется известным выражением: N(N-1)/2. При обоюдном измерении расстояний между двумя спутниками число измеренных межспутниковых дальностей будет равно, соответственно, N(N-1). В полученных измерениях содержатся следующие неизвестные переменные: N(N-1)/2 истинных расстояний между N спутниками, (N-1) линейно независимых ошибок взаимной синхронизации часов N спутников (остальные (N-1)(N/2-1) определяются их линейными комбинациями) и N инструментальных погрешностей передатчиков N спутников, т.е. общее число неизвестных переменных составляет N(N-1)/2+N-1+N. Приравнивая общее число измерений к числу неизвестных переменных, имеем следующее уравнение:

N(N-1)/2=2N-1

или

N²-5N+2=0,

откуда легко определяется число спутников, необходимое и достаточное для решения поставленной задачи идентификации:

N=5.

(Если истинные расстояния между спутниками известны - например, измерены с высокой точностью лазерными дальномерами, то число неизвестных переменных сокращается до 2N-1 и уравнение, определяющее число спутников, принимает вид: N²-3N+1=0, откуда N=3).

В принятых обозначениях измеренные расстояния (псевдодальности) Z_ij между пятью навигационными спутниками 1_i, i=1,5 (фиг. 1) могут быть представлены следующим образом:

где ΔT₁₂, ΔT₁₃, ΔT₅₃, ΔT₂₃…ΔT₃₄, ΔT₅₄, ΔT₂₄ - погрешности взаимной синхронизации часов спутников 1₁, 1₂, 1₃, 1₄ и 1₅,

R₁₃, R₂₃, R₁₂…R₅₃, R₂₄, R₅₄ - истинные дальности между спутниками,

W_S1, W_S2, W_S3, W_S4, W_S5 - инструментальные погрешности передатчиков спутников 1₁, 1₂, 1₃, 1₄ и 1₅, соответственно.

Учитывая очевидные соотношения:

ΔT_ji=-ΔT_ij, ΔT_jk=ΔT_ik-ΔT_ij=ΔT_k-ΔT_j, i, j, k=1, 2…5,

система (4) из 20 уравнений с 35 неизвестными может быть сведена к системе 20 уравнений с 19 неизвестными - десятью истинными дальностями R₁₃, R₂₃, R₁₂, …, R₄₃, R₂₄, R₅₄, четырьмя независимыми погрешностями взаимной синхронизации часов спутников (выбор определяемых погрешностей принципиального значения не имеет, поэтому выберем далее в качестве независимых переменных погрешности ΔT₁₂, ΔT₁₃, ΔT₁₄, ΔT₁₅) и инструментальными погрешностями передатчиков W_S1, W_S2, W_S3, W_S4, W_S5:

и легко решается любым из известных способов решения линейных алгебраических уравнений непосредственно на борту каждого из спутников 1₁, 1₂, 1₃, 1₄ и 1₅. Т.к. при этом одно избыточное уравнение может быть исключено, возникает возможность дополнительного формирования еще C 20 19 − 1 = 19 систем уравнений, аналогичных (5), для их параллельного решения с целью повышения точности идентификации - за счет, например, усреднения полученных результатов. В данном случае решается не только задача текущего определения погрешностей взаимной синхронизации часов всех спутников и инструментальных погрешностей их передатчиков, используемых, как показано далее, для компенсации помех в сигнале навигационного приемника объекта, но и расстояний между спутниками, используемых, в свою очередь, в качестве дополнительной информации для повышения точности измерения текущего местоположения спутников.

Таким образом, определение всех упомянутых выше параметров позволяет осуществить идентификацию как расстояний между спутниками, так и ошибок синхронизации их собственных часов и инструментальных погрешностей передатчиков.

Компенсация погрешностей спутникового сообщения в навигационном приемнике основана на том, что для решения навигационной задачи спутниковые сообщения принимаются, как правило, не менее чем от четырех спутников [ГЛОНАСС. Принципы построения и функционирования / Под ред. А.И. Перова, В.Н. Харисова. - 3-е изд., перераб. - М.: Радиотехника, 2005. - 688 с.], что позволяет формировать различные линейные комбинации сигналов, принимаемых от разных спутников. Так, разность сигналов псевдодальностей, принятых от двух спутников - i-го и j-го, с учетом (1), имеет вид:

где принято вытекающее из практики спутниковой навигации допущение об идентичности помех, обусловленных прохождением через ионосферу и тропосферу радиосигналов спутников, находящихся в зоне видимости одного и того же объекта.

Как видно из (6), разность сигналов Z_Ri-Z_Rj любых двух спутников содержит помеховые составляющие ΔT_ij, W_Si, W_Sj, которые уже известны из принятого спутникового сообщения и могут быть скомпенсированы (и не содержит остальных помех, приведенных в (1): ошибок часов приемника, его инструментальных погрешностей и др.).

В результате, обработке - применению стандартной итеративной процедуры решения системы нелинейных уравнений (7) относительно координат ξ, η, ζ, подлежат сигналы, содержащие только истинную информацию о координатах объекта, что позволяет существенно повысить общую точность решения навигационной задачи:

где ΔZ_ij - разность псевдодальностей, принятых от i-го и j-го спутников;

ΔZ_ik - разность псевдодальностей, принятых от i-го и k-го спутников;

ΔZ_kj - разность псевдодальностей, принятых от k-го и j-го спутников.

Алгоритм технической реализации предлагаемого способа рассмотрим по шагам на примере спутника 1 (фиг. 1).

1. Передача навигационных сообщений к спутникам 1₂, 1₃, 1₄, 1₅.

2. Прием навигационных сообщений от спутников 1₂, 1₃, 1₄, 1₅ (выполняется одновременно с п. 1).

3. Определение псевдодальностей Z₂₁, Z₃₁, Z₄₁, Z₅₁ до спутников 1₂, 1₃, 1₄, 1₅.

4. Параллельная передача полученных значений псевдодальностей Z₂₁, Z₃₁, Z₄₁, Z₅₁ на спутники 1₂, 1₃, 1₄, 1₅.

5. Прием значений псевдодальностей Z₁₂, Z₃₂, Z₄₂, Z₅₂ от спутника 1₂ (выполняется одновременно с п. 4).

6. Прием значений псевдодальностей Z₁₃, Z₂₃, Z₄₃, Z₅₃ от спутника 1₃ (выполняется одновременно с п. 4).

7. Прием значений псевдодальностей Z₁₄, Z₂₄, Z₃₄, Z₅₄ от спутника 1₄ (выполняется одновременно с п. 4).

8. Прием значений псевдодальностей Z₁₅, Z₂₅, Z₄₅, Z₃₅ от спутника 1₅ (выполняется одновременно с п. 4).

9. Решение системы уравнений (5) и вычисление истинных дальностей R₁₃, R₂₃, R₁₂, …, R₅₃, R₂₄, R₅₄; погрешностей взаимной синхронизации часов ΔT₁₂, ΔT₁₃, ΔT₁₄, ΔT₁₅ и инструментальных погрешностей передатчиков W_S1, W_S2, W_S3, W_S4, W_S5.

10. Передача в спутниковом сообщении истинных дальностей R_ij между всеми спутниками, погрешностей взаимной синхронизации часов и значений инструментальных погрешностей передатчиков для последующей корректировки спутниковых измерений (1).

11. Решение системы уравнений (7) и вычисление координат навигационного приемника.

Предложенный способ идентификации параметров навигационных спутников позволяет, используя простые методы радио- и лазерных измерений, во-первых, существенно повысить точность синхронизации хода часов на всех навигационных спутниках группировки (что особенно важно для системы ГЛОНАСС, наземные станции синхронизации времени которой расположены только на территории РФ), во-вторых, определять истинные дальности R_ij между спутниками непосредственно на борту спутника, снижая тем самым вычислительную нагрузку на приемники потребителей и телеметрических станций слежения, и, в-третьих, повысить общую точность решения навигационной задачи за счет компенсации основных помех в принятом навигационном сообщении. При этом также неизбежно увеличение точности определения рассмотренных пространственно-временных параметров в силу большей точности межспутниковых измерений, осуществляемых в космосе, по сравнению с телеметрическими, подверженными влиянию атмосферных возмущений.

Способ идентификации параметров навигационных спутников, заключающийся в том, что в группе из пяти навигационных спутников, находящихся в зоне прямой видимости, реализуются одновременные передача навигационных сообщений от каждого спутника к каждому и их прием каждым спутником от каждого, определение межспутниковых псевдодальностей и их передача на другой спутник с последующим решением на каждом спутнике системы девятнадцати линейных алгебраических уравнений, в результате которого определяются истинные дальности между спутниками, погрешности взаимной синхронизации часов спутников и инструментальные погрешности передатчиков, после чего погрешности взаимной синхронизации часов спутников и инструментальные погрешности передатчиков передаются в навигационных сообщениях и компенсируются в навигационном приемнике при определении координат навигационного приемника на основе решения системы трех нелинейных уравнений, каждое из которых сформировано по разности измеренных псевдодальностей между двумя спутниками.