Способ извлечения из доплеровских портретов воздушных объектов признаков идентификации с использованием метода сверхразрешения

Способ извлечения из доплеровских портретов воздушных объектов признаков идентификации с использованием метода сверхразрешения

Иллюстрации

Показать все

Реферат

Изобретение относится к радиолокационным методам и предназначено для извлечения из доплеровских портретов (ДпП) воздушных объектов (ВО) признаков идентификации, а именно частоты и амплитуды спектральных откликов, соответствующих рассеивающим центрам (РЦ) поверхности ВО.

В настоящее время использование векторных признаков классификации и идентификации объектов в виде портретов и индикатрис является общепринятым. Оно описано, например, в [1-8]. Однако признаки отождествления объектов, формируемые, как правило, методом физического или математического моделирования, получают обычными спектральными или корреляционными методами. Получаемые признаки не оптимизируются в интересах повышения их информативности, что снижает потенциальное качество классификации объектов. Для формирования векторных признаков, классификация объектов по которым не будет приводить к дополнительным ошибкам, необходим поиск новых путей, подходы к некоторым из которых описаны в [5-8].

На сегодняшний день известен способ извлечения из ДпП ВО признаков идентификации, реализуемый с соблюдением принципов электродинамического масштабного моделирования в безэховой камере [1, 2, 9-16].

Способ заключается в том, что исследуемый объект изготавливают в уменьшенном размере, причем коэффициент масштабирования выбирают таким, чтобы модель объекта позволяла поместить ее в безэховую камеру и закрепить на поворотном устройстве. Длину волны передающего радиолокационного устройства выбирают из условия выполнения требований электродинамического подобия по формуле

где λ_рлс - длина волны реальной радиолокационной станции (РЛС), в интересах которой проводятся исследования [16]; L_мод - размер модели объекта; L_об - размер реального объекта; K_мод=L_об/L_мод ^_ коэффициент или масштаб моделирования.

Модель объекта изготавливают из материала, отражающие свойства которого соответствуют отражающим свойствам реального объекта. Модель объекта помещают на поворотную радиопоглощающую или радиопрозрачную платформу. Излучают в направлении масштабной модели объекта радиолокационные сигналы и принимают с помощью радиоприемной системы, расположенной внутри безэховой камеры, отраженные моделью объекта сигналы. Проводят согласованную корреляционно-фильтровую обработку принятых сигналов от масштабной модели, объекта, усиливают их, разделяют на фазовом детекторе на квадратурные (синусную и косинусную) составляющие. С квадратурными составляющими, соответствующими изменению азимутального положения масштабной модели объекта на единицы градусов, проводят операцию дискретного преобразования Фурье (ПФ) для получения ДпП масштабной модели объекта. Из структуры ДпП извлекают признаки идентификации, а именно частоты и амплитуды спектральных откликов в точках достижения амплитудами ДпП максимумов.

Однако этот способ не может использоваться для работы по реальным летательным аппаратам, так как рассчитан на постоянную угловую скорость изменения ракурса ВО, что в реальных условиях выполняется крайне редко. К тому же формируемые таким способом ДпП не в полной мере соответствуют реальным, так как полную адекватность модели обеспечить затруднительно. И наконец, в реальных условиях угол места ВО не является нулевым и даже изменяется в процессе накопления отраженных сигналов, а в безэховой камере он неизменен, что ведет к различиям получаемых ДпП.

Известен способ извлечения из ДпП ВО признаков идентификации в условиях излучения радиолокационных сигналов в свободном пространстве при использовании масштабной модели объекта [17]. Способ заключается в том, что масштабную модель объекта с коэффициентом масштабирования не более нескольких единиц вместе с опорно-поворотным устройством (ОПУ) подвешивают с помощью тросов и растяжек в свободном пространстве на высоте нескольких десятков метров над землей. Тросы из радиопрозрачного материала, удерживающие масштабную модель объекта с ОПУ, закрепляют на вышках, находящихся на расстоянии, при котором эти вышки выходят за пределы характеристики направленности антенны приемо-передающей РЛС. В качестве экспериментальной РЛС используют типовую РЛС с импульсным зондированием и развязкой передающего и приемного устройства или РЛС с отдельным передающим и отдельно расположенным приемным устройством. Для вращения масштабной модели объекта используют ОПУ с понижающим угловую скорость редуктором. Излучают в направлении масштабной модели объекта зондирующие сигналы (ЗС) и принимают отраженные от нее сигналы, усиливают их и компенсируют специальным методом паразитные отражения от местных предметов, ОПУ и вышек. После записи параметров отраженных сигналов для всех азимутальных положений масштабной модели объекта, опираясь на данные о временах приема отраженных сигналов, выделяют из общего генерального массива данных об отраженных сигналах частные выборки (ЧВ) данных об амплитудах и фазах сигналов, полученных на выбранных или заданных заблаговременно интервалах инверсного синтезирования (ИИС). Проводят с массивом комплексных амплитудно-фазовых отсчетов каждой ЧВ операцию дискретного ПФ [18, 19], в результате для каждого ИИС (для каждой ЧВ) формируют спектральный комплексный массив отсчетов, огибающую которого считают ДпП масштабной модели объекта, соответствующим по времени середине этого ИИС, т.е. времени приема отраженного сигнала, записанного в середине используемой ЧВ [20, 21]. Из структуры сформированного ДпП извлекают такие признаки идентификации, как частоты и амплитуды спектральных откликов.

Данный способ также является исследовательским и для работы по реальным объектам эффективно применяться не может, так как не оснащен адаптивными алгоритмами обработки в условиях нелинейного изменения ракурса локации.

Известен на практике еще один способ извлечения из ДпП ВО признаков идентификации [22]. Способ заключается в том, что в направлении реального объекта с помощью реальной РЛС с диапазоном волн от единиц до десятков сантиметров излучают сверхвысокочастотные импульсные сигналы одинаковой частоты, принимают отраженные объектом сигналы, усиливают эти сигналы на высокой частоте. Затем проводят их частотную фильтрацию, переводят их на промежуточную частоту, проводят основное усиление на промежуточной частоте, проводят в пределах периода повторения импульсов согласованную обработку принятых сигналов сверткой с ЗС для выделения пиков их откликов, в точках пиков откликов отраженных сигналов фиксируют их амплитуду, фазу и точное время приема, записывают эти параметры для всех по очереди периодов повторения на магнитный носитель в виде генерального массива данных, содержащего амплитуды, фазы и времена приема сигналов, выбирают величину ИИС Т_с на основе необходимого спектрального разрешения по формуле , где - необходимая разрешающая способность в частотной области, выделяют из данных об амплитудах, фазах и временах приема частную выборку, соответствующую исследуемому ИИС. Переводят амплитуду A_s и фазу φ_s каждого s-го отсчета с помощью аналого-цифрового преобразователя (АЦП) в цифровой вид и далее - в комплексную форму вида A_sexp(jφ_S), где A_s и φ_s - соответственно амплитуда и фаза пика отклика s-го отраженного сигнала. Далее проводят с данными частной выборки комплексных отражений от объекта операцию дискретного преобразования Фурье и формируют в результате спектральный массив, выражающий своей огибающей ДпП объекта. Из структуры сформированного ДпП извлекают признаки идентификации, а именно частоты и амплитуды спектральных откликов.

Данный способ опирается на применение реальных ВО, использует реальные ЗС на реальных радиолокационных дальностях. Однако даже он имеет недостаток, состоящий в том, что ДпП формируется неадаптивно, в предположении постоянства угловой скорости поворота ВО, что приводит к снижению информативности признаков из структуры ДпП, то есть к снижению его пригодности для практических задач идентификации.

Наиболее близким техническим решением является способ извлечения из ДпП ВО признаков идентификации, описанный в [23]. Для построения ДпП согласно этому способу использовалась пачка отраженных сигналов длительностью 0,5 с. Это обеспечивало, с одной стороны, разрешающую способность по частоте не хуже 2 Гц, а с другой стороны, из-за проявления дестабилизирующих факторов, приводило к незначительному искажению структуры ДпП.

Способ заключается в том, что в направлении реального ВО излучают ЗС одинаковой частоты и последовательно принимают отраженные от него сигналы. После обнаружения традиционным радиолокационным способом ВО переводят РЛС в режим автоматического сопровождения и сопровождают ВО по угловым координатам и дальности, а после определения дальности D до ВО [24] дискретизируют с помощью АЦП и записывают в память ЭВМ амплитуду A_s и фазу φ_s принятых сигналов и просочившихся в приемный тракт излученных сигналов каждого i-го периода повторения с периодом дискретизации Δt, получая в каждом периоде повторения S дискретных отсчетов (фиг. 1). При этом в пределах длительности ЗС для каждого периода повторения будет укладываться J дискретных отсчетов (фиг. 2). После этого с преобразованными сигналами проводят цифровую согласованную фильтрацию в каждом i-м периоде повторения, то есть проводят свертку принятых (отраженных от ВО) сигналов определенных периодов зондирования с оцифрованными комплексно-сопряженными ЗС этих же периодов зондирования для получения откликов согласованного цифрового фильтра (фиг. 3). Алгоритм цифровой согласованной фильтрации аналитически выражается следующим образом

где i=1…I; s=1…(S-J); - комплексные значения, получаемые после сжатия отраженного сигнала цифровым фильтром, соответствующие s-му отсчету отраженного сигнала в i-м периоде повторения; , - значения амплитуды и фазы отраженного сигнала, соответствующие (s+j-1)-му отсчету продискретизированного отраженного сигнала в i-м периоде повторения импульсов; , - значения амплитуды и фазы излученного сигнала, соответствующие j-му отсчету продискретизированного ЗС в i-м периоде повторения импульсов; I - количество периодов повторения ЗС, укладывающееся на интервале регистрации данных.

После этого рассчитывают время прохождения излученного сигнала τ_во до ВО и обратно по формуле

где - скорость распространения электромагнитных волн.

Затем определяют предполагаемый номер отсчета g, на который при дальности D будет приходиться пик отраженного от ВО сигнала, по формуле

где round - операция округления значения до следующего целого числа.

После этого в памяти электронно-вычислительной машины (ЭВМ) РЛС формируют массив отражений H_g (фиг. 4), в первую строку которого записывают номера используемых при анализе отражений i-x периодов повторения, во вторую - амплитуды g-x отсчетов сжатого сигнала, которые соответствуют пикам откликов отраженного от ВО сигнала в i-x периодах повторения, в третью - фазы g-x отсчетов сжатого сигнала, которые соответствуют пикам откликов отраженных сигналов в i-x периодах повторения, в четвертую - моменты времени t_i=[(i-1)S+g+round(J/2)]Δt, соответствующие амплитудам и фазам сжатых отраженных от ВО сигналов в i-x периодах повторения. Дополнительные round(J/2) отсчета, учитываемые при расчете i-x моментов времени t_i, обусловлены тем, что пик отклика в каждом периоде повторения приходится на середину длительности принимаемого отраженного от ВО сигнала.

Из амплитудных значений массива H_g формируют зависимость, которая графически представляет собой амплитудную отражательную характеристику (ОХ) ВО (фиг. 5). После этого из созданной зависимости, начиная с первого отсчета, последовательно извлекают выборки длительностью Т_L=0,5 с каждая, смещенные друг относительно друга на один отсчет (фиг. 6). Каждая выборка содержит N=round(T_L/T_и) дискретных отсчетов, где T_и - период повторения импульсов. Для каждой выборки формируют автокорреляционную функцию [25, 26] (фиг. 7) и определяют величину интервала корреляции τ_к (момент времени, когда автокорреляционная функция первый раз становится равной нулю). Затем выбирают минимальную среди всех интервалов корреляции τ_к величину τ_{к мин}, определяют оценочное время корреляции τ_оц, равное величине порядка 0,5 τ_{к мин}. Начиная с первого отсчета (элемента), последовательно выделяют из массива H_g смещенные друг относительно друга на w=round(τ_оц/Т_и) отсчетов d-e пары смежных выборок, учитывая, что d=1…round[(I-N)/w] (фиг. 7).

После этого с помощью амплитуд выделяемых d-x пар выборок рассчитывают коэффициенты корреляции z_d по формуле [26]

где y_n+(d-1)w, y_n+dw - амплитудные значения, соответствующие [n+(d-1)w]-му дискретному отсчету первой выборки и [n+dw]-му отсчету второй выборки в d-й паре соответственно; m_1,d, m_2,d - математические ожидания [26] амплитудных значений ОХ в первой (индекс 1) и во второй (индекс 2) выборках d-й пары соответственно; σ_1,d, σ_2,d - среднеквадратические отклонения амплитудных значений в первой и во второй выборках d-й пары соответственно.

Затем в памяти ЭВМ РЛС формируют массив H_z, в первую строку которого записывают номера пар выборок d, во вторую - соответствующие им коэффициенты корреляции z_d (фиг. 8). Из значений коэффициентов корреляции z_d массива H_z формируют зависимость, которая графически представляет собой корреляционную характеристику (КХ) ВО (фиг. 9). В сформированной КХ каждой d-й паре смежных выборок ОХ соответствует один d-й коэффициент корреляции z_d.

Со сформированной КХ проводят сглаживание цифровым образом методом наименьших квадратов [27], то есть устраняют локальные максимумы и минимумы, оставляя только глобальные (фиг. 10). В сглаженной КХ определяют такой ее участок между соседними глобальными максимумом и минимумом, на котором максимальное z_{d max} и минимальное z_{d min} значения коэффициента корреляции имеют наибольшее отличие (фиг. 10). На этом участке находят точку со значением коэффициента корреляции z_{d с}, которое наиболее точно соответствует величине [(z_{d max}-z_{d min})/2] (фиг. 10). Затем используют эту точку как середину информативного интервала длительностью Т_ии=0,5 с. По номеру z_{d c} пары выборок ОХ определяют соответствующий этой паре [round{(d_c-1)w+[(N+w)/2]}]-й номер периода повторения в ОХ, где d_c - номер пары выборки, соответствующий середине информативного интервала. Находят номера отсчетов в ОХ, которые по времени сдвинуты относительно середины информативного интервала на 0,25 с по формулам

где i_н - номер отсчета ОХ массива H_g, соответствующий началу информативного интервала; i_к - номер отсчета ОХ массива H_g, соответствующий концу информативного интервала.

Найденный информативный участок (интервал) КХ соответствует средней угловой скорости изменения ракурса локации ВО, обусловленной только перемещением центра масс ВО по траектории. На данном информативном интервале структура ДпП ВО не будет претерпевать существенных изменений из-за влияния траекторных нестабильностей, что будет способствовать сохранению идентификационных возможностей ДпП [23].

Затем в памяти ЭВМ РЛС создают массив Н_и (фиг. 11), в первую строку которого записывают µ-e номера периодов повторения с 1 по М-й, причем M=round(0,5/T_и), а µ-й номер в пределах массива Н_и соответствует (i_н+µ-1)-му номеру в исходной ОХ, во вторую - амплитуды µ-х отсчетов ОХ, принадлежащих информативному интервалу, в третью - фазы µ-x отсчетов ОХ, принадлежащих информативному интервалу, в четвертую - моменты времени t_µ=(i_н+µ-1)Т_и, соответствующие амплитудам и фазам отраженных сигналов в µ-x периодах повторения, имеющих такую нумерацию в пределах ИИС). Первый элемент массива Н_и соответствует началу информативного интервала, то есть i-му элементу массива H_g а последний элемент массива H_и соответствует концу информативного интервала, то есть i_к-му элементу массива H_g.

После этого проводят операцию дискретного преобразования Фурье с комплексными значениями выборки, состоящей из 8 первых отсчетов массива Н_и. В результате получают начальный низкоинформативный доплеровский спектр (НДС). В полученном начальном НДС определяют частоту Доплера , которая соответствует максимальной по амплитуде составляющей спектра.

Затем определяют радиальную скорость ВО в начале информативного интервала по формуле

где λ - длина волны излучаемого сигнала.

После этого проводят операцию дискретного преобразования Фурье с комплексными значениями выборки, состоящей из 8 последних отсчетов массива Н_и. В результате получают конечный НДС. В полученном конечном НДС определяют частоту Доплера , которая соответствует максимальной по амплитуде составляющей спектра.

Затем определяют радиальную скорость ВО в конце информативного интервала по формуле

После этого определяют среднюю радиальную скорость ВО в пределах информативного ИИС по формуле

Затем определяют радиальное ускорение a _r ВО на выбранном информативном интервале по формуле

Далее на основе рассчитанных значений средней радиальной скорости и ускорения a _r рассчитывают величину компенсируемой фазы для каждого t_µ-го момента времени по формуле

После этого проводят компенсацию фазового влияния радиального движения ВО на выбранном информативном интервале путем изменения фазы каждого µ-го элемента массива Н_и на величину по формуле

где знак «-» соответствует движению ВО в направлении РЛС (приближению), а знак «+» соответствует удалению ВО.

Затем в памяти ЭВМ РЛС создают массив Н_с (фиг. 12), в первую строку которого записывают номера периодов повторения с 1 по М-й, во вторую - амплитуды отсчетов ОХ, принадлежащих информативному интервалу, в третью - скомпенсированные фазы g-x отсчетов ОХ, принадлежащих информативному интервалу, в четвертую - моменты времени t_µ, соответствующие амплитудам и фазам отраженных сигналов в µ-х периодах повторения.

С использованием данных массива Н_с формируют ДпП ВО в выбранном информативном интервале путем проведения операции дискретного преобразования Фурье с комплексными амплитудно-фазовыми значениями по формуле

где k=1…М; - комплексное амплитудно-фазовое значение спектра, соответствующее k-му отсчету; - комплексное амплитудно-фазовое значение массива, соответствующее µ-му отсчету.

Анализируют полученный ДпП и извлекают из его структуры признаки идентификации, а именно частоты и амплитуды локальных спектральных составляющих (откликов). При идентификации предполагают использовать число спектральных составляющих в ДпП ВО, их взаимное частотное расположение и соотношение амплитуд составляющих.

Согласно теоретическим положениям структура ДпП должна определяться размерами объекта, величиной интервала инверсного синтезирования (ИИС) и угловой скоростью поворота объекта [23, 28]. С одной стороны, для улучшения разрешающей способности требуется увеличивать время T_ии. Однако при увеличении времени инверсного синтезирования (информативного интервала) Т_ии в его пределы могут войти отсчеты ОХ, которым соответствуют экстремумы ее КХ, а они, в свою очередь, являются моментами начала или конца интервала интенсивного влияния траекторных нестабильностей (а именно, рысканий ВО по курсу, крену и тангажу, вызванных его движением в турбулентной атмосфере). При этом информативность ДпП ВО будет снижаться, сам портрет будет искажаться, что негативно повлияет на процесс классификации ВО по его структуре. Поэтому целесообразно, чтобы время инверсного синтезирования T_ии составляло не более 0,3-0,5 с.Однако ДпП при этом будет слабоинформативным, что негативно повлияет на процесс идентификации или классификации. Таким образом, необходимо, с одной стороны, ограничивать ИИС, а с другой - обеспечить максимально возможное разрешение по частоте. Это противоречие может быть разрешено с привлечением так называемых методов сверхразрешения [29].

Задачей изобретения является разработка способа извлечения из ДпП ВО признаков идентификации, при котором за счет использования метода сверхразрешения при ограниченном времени инверсного синтезирования (менее 0,5 с) обеспечивается высокая разрешающая способность по частоте, способствующая повышению информативности признаков идентификации, заключенных в структуре ДпП.

Для решения задачи изобретения предлагается провести методом линейного предсказания проверку структуры ДпП ВО на возможное наличие в ней дополнительных спектральных составляющих, соответствующих РЦ на освещенной поверхности ВО, которые при проведении стандартной операции дискретного преобразования Фурье с комплексными значениями ОХ ВО по причине низкой разрешающей способности выявлены не были. В получаемом способом-прототипом ДпП ВО несколько соседних истинных спектральных откликов от РЦ могли «объединяться» в один отклик, что усложняло последующий процесс идентификации.

Способ извлечения из ДпП ВО признаков идентификации с использованием метода сверхразрешения заключается в том, что в направлении ВО с помощью реальной РЛС сопровождения излучают сверхвысокочастотные импульсные сигналы одинаковой частоты, а затем принимают отраженные ВО сигналы. После обнаружения ВО переводят РЛС в режим автоматического сопровождения по угловым координатам и дальности. Определяют дальность D до ВО, после чего дискретизируют с помощью АЦП с периодом дискретизации Δt и записывают в память ЭВМ амплитуду A_s и фазу φ_s отраженных сигналов, а также просочившихся в приемный тракт излученных сигналов каждого i-го периода повторения, получая при этом в каждом периоде повторения S дискретных отсчетов (фиг. 1). При этом в каждом периоде повторения в пределах длительности просочившегося ЗС будет укладываться J дискретных отсчетов (фиг. 2). После оцифровки отраженных сигналов с ними проводят цифровую согласованную фильтрацию в каждом i-м периоде повторения для получения откликов согласованного цифрового фильтра (фиг. 3), то есть проводят свертку принятых отраженных от ВО сигналов с оцифрованными комплексно-сопряженными ЗС в одних и тех же периодах повторения по формуле (2).

После этого по формуле (3) рассчитывают время прохождения излученного сигнала τ_во до ВО и обратно. Затем по формуле (4) определяют предполагаемый номер отсчета g, на который при дальности D будет приходиться пик отраженного от ВО сигнала.

После этого в памяти ЭВМ РЛС формируют массив отражений H_g (фиг. 4). В первую строку этого массива записывают номера используемых при анализе отражении i-х периодов повторения, во вторую - амплитуды g-x отсчетов сжатого сигнала, которые соответствуют пикам откликов отраженного от ВО сигнала, в i-х периодах повторения, в третью - фазы g-x отсчетов сжатого сигнала, которые соответствуют пикам откликов отраженных сигналов в i-х периодах повторения, в четвертую - моменты времени t_i=[(i-1)S+g+round(J/2)]Δt, соответствующие амплитудам и фазам _g сжатых отраженных сигналов от ВО в i-х периодах повторения.

Из амплитудных значений массива H_g формируют зависимость, которая графически представляет собой амплитудную ОХ ВО (фиг. 5). После этого, начиная с первого отсчета, из созданной зависимости последовательно извлекают выборки длительностью T_L=0,5 с каждая, смещенные друг относительно друга на один отсчет (фиг. 6). Каждая выборка содержит N=round (T_L/T_и) дискретных отсчетов. Для каждой выборки формируют автокорреляционную функцию (фиг. 7) и определяют величину интервала корреляции τ_k (момент времени, когда автокорреляционная функция первый раз принимает значение, равное нулю). После этого выбирают минимальную среди всех интервалов корреляции τ_k величину τ_{k мин}, определяют оценочное время корреляции τ_оц, равное величине порядка 0,5τ_{k мин}. Начиная с первого отсчета, последовательно выделяют из массива H_g смещенные друг относительно друга на w=round(τ_оц/Т_и) отсчетов d-e пары смежных выборок, учитывая, что d=1…round[(I-N)/w] (фиг. 7).

Затем по формуле (5) с помощью амплитуд выделяемых d-x пар выборок рассчитывают коэффициенты корреляции z_d. После этого в памяти ЭВМ РЛС формируют массив H_z. В первую строку этого массива записывают номера пар выборок d, во вторую - соответствующие им коэффициенты корреляции z_d (фиг. 8). После этого формируют из значений коэффициентов корреляции z_d массива H_z зависимость, которая графически представляет собой КХ ВО (фиг. 9).

Проводят сглаживание сформированной КХ методом наименьших квадратов цифровым образом, то есть устраняют локальные максимумы и минимумы, оставляя только глобальные (фиг. 10). В сглаженной КХ определяют такой ее участок между соседними глобальными максимумом и минимумом, на котором максимальное z_{d max} и минимальное z_{d min} значения коэффициента корреляции имеют наибольшее отличие (фиг. 10). На этом участке находят точку со значением коэффициента корреляции z_{d c}, которое наиболее точно соответствует величине [(z_{d max}-z_{d min})/2] (фиг. 10). Затем используют эту точку как середину информативного интервала длительностью T_ии=0,5 с. По номеру z_{d c} пары выборок ОХ определяют соответствующий ему [round((d_c-1)w+[(N+w)/2])]-й номер периода повторения в ОХ. По формулам (6) и (7) находят номера отсчетов в ОХ, которые по времени сдвинуты относительно середины информативного интервала на 0,25 с.

После этого в памяти ЭВМ РЛС создают массив Н_и (фиг. 11). В первую строку этого массива записывают µ-e номера периодов повторения с 1 по М-й, причем М=round(0,5/T_и), а µ-й номер в пределах массива Н_и соответствует (i_н+µ-1)-му номеру в исходной ОХ, во вторую - амплитуды µ-x отсчетов ОХ, принадлежащих информативному интервалу, в третью - фазы µ-x отсчетов ОХ, принадлежащих информативному интервалу, в четвертую - моменты времени t_µ=(i_н+µ-1)Т_и, соответствующие амплитудам и фазам отраженных сигналов в µ-x периодах повторения (в пределах ИИС). Первый элемент массива H_и соответствует началу информативного интервала, то есть i_н-му элементу массива H_g, а последний элемент массива Н_и соответствует концу информативного интервала, то есть i_к-му элементу массива H_g.

Затем с комплексными значениями выборки, состоящей из 8-ми первых отсчетов массива Н_и, проводят операцию дискретного преобразования Фурье, в результате которой получают начальный НДС. В полученном начальном НДС определяют частоту Доплера , которая соответствует максимальной по амплитуде составляющей спектра.

После этого по формуле (8) определяют радиальную скорость ВО в начале информативного интервала .

Затем с комплексными значениями выборки, состоящей из 8-ми последних отсчетов массива Н_и, проводят операцию дискретного преобразования Фурье, в результате которой получают конечный НДС. В полученном конечном НДС определяют частоту Доплера , которая соответствует максимальной по амплитуде составляющей спектра.

После этого по формуле (9) определяют радиальную скорость ВО в конце информативного интервала .

Затем по формуле (10) определяют среднюю радиальную скорость ВО в пределах информативного интервала.

После этого по формуле (11) определяют радиальное ускорение a _r ВО на выбранном информативном интервале.

Далее по формуле (12) на основе рассчитанных значений средней радиальной скорости и ускорения a _r рассчитывают величину компенсируемой фазы для каждого t_µ-го момента времени.

После этого по формуле (13) проводят компенсацию фазового влияния радиального движения ВО на выбранном информативном интервале путем изменения фазы каждого µ-го элемента массива Н_и на величину .

Затем в памяти ЭВМ РЛС из элементов массива Н_и создают массив Н_с с заменой на соответствующие (фиг. 12). В первую строку этого массива записывают номера периодов повторения с 1-го по М-й, во вторую - амплитуды g-x отсчетов ОХ, принадлежащих информативному интервалу, в третью - скомпенсированные фазы µ-x отсчетов ОХ, принадлежащих информативному интервалу, в четвертую - моменты времени t_µ, соответствующие амплитудам и фазам отраженных сигналов в µ-x периодах повторения.

После этого проводят операцию дискретного преобразования Фурье со всеми µ-ми комплексными величинами , составленными из элементов массива Н_с. В результате получают предварительный ДпП, в котором определяют частоту, соответствующую его максимальному амплитудному значению, и используют эту частоту как предварительную оценку частоты .

Далее определяют предполагаемое число гармоник Р в спектре идентифицируемого ВО [18]. Это число Р выбирают равным максимально возможному числу ярко выраженных РЦ на поверхности ВО в квазиоптической области отражения радиоволн, имеющему для крупноразмерного ВО величину порядка 10, а для среднеразмерного и малоразмерного ВО - не более 5. Для определения наиболее подходящего значения числа гармоник Р целесообразно по причине компромисса между высоким поперечным разрешением и возможным появлением ложных спектральных откликов провести несколько процедур формирования ДпП ВО, используя в каждой из них одно из значений числа гармоник Р, близкого к вышеуказанным.

Затем, начиная с первого элемента массива Н_с, последовательно извлекают A=round(3P/2) выборок, состоящих из Q≈trunc(M/A) элементов и смещенных друг относительно друга на Q элементов (на длительность выборки), где trunc - операция округления значения до предыдущего целого числа.

После этого определяют комплексные суммы Q элементов массива Н_с внутри каждой а-й выборки с дополнительным фазированием на частоте , соответствующие а-м частным выборкам, где а=1…А, по формуле

Затем в памяти ЭВМ РЛС создают массив Н_а (фиг. 13). В первую строку этого массива записывают а-е номера выборок с 1-й по А-й, а во вторую -соответствующие комплексные суммы .

После этого для выбранного числа Р, из массива Н_а, состоящего из А комплексных сумм , формируют модифицированным ковариационным методом [29] матрицу данных U_p размерностью (Р+1)×[2(А-Р)] по формуле

Для случая, когда, например, Р=5, число комплексных сумм A будет равно А=8, и матрица данных U_P примет вид

Затем рассчитывают оценку корреляционной матрицы размерностью [2(А-Р)]×[2(А-Р)], где - эрмитово-сопряженная матрица, соответствующая матрице U_P, и составляют систему нормальных уравнений вида

где c_P - вектор из Р строк и 1-го столбца, включающий Р неизвестных коэффициентов; - среднее значение квадратов ошибок линейного предсказания вперед и назад порядка Р; - комплексное значение первой строки первого столбца матрицы R^-1; R^-1 - матрица, обратная матрице R; 0_P - Р-элементный вектор-столбец, включающий нулевые значения.

Систему (18) для удобства ее решения относительно неизвестного вектора с_Р записывают в следующем виде

Решая систему (19) относительно неизвестного вектора с_Р, получают оценки коэффициентов вектора с_Р, которые затем используют для вычисления спектральной функции

где - текущая частота, соответствующая диапазону частот от -(0,5/T_и) до +(0,5/T_и).

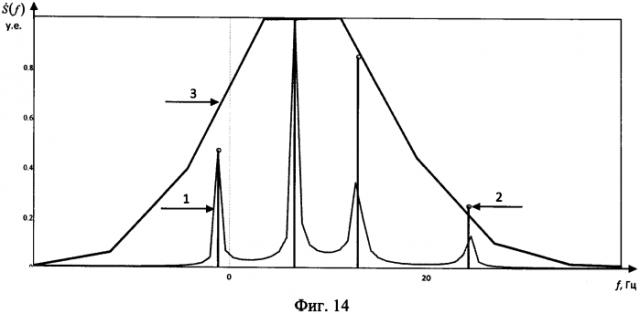
Сформированную спектральную функцию принимают за прототип ДпП ВО, пример которого показан на фиг. 14-16 (выносимая линия 1). Далее подсчитывают число локальных максимумов спектральной функции