Способ определения динамического коэффициента внешнего трения

Способ определения динамического коэффициента внешнего трения

Иллюстрации

Показать все

Реферат

Изобретение относится к области механических испытаний материалов, в частности к определению динамического коэффициента трения при взаимном перемещении образцов.

Известны способы определения динамического коэффициента внешнего трения, состоящие в непосредственном измерении силы трения на образцах при их взаимном перемещении.

Недостатком таких способов является необходимость применения силоизмерительных механизмов, усложняющих применяемые устройства.

Существуют способы и устройства, позволяющие исключить непосредственное измерение силы при определении динамического коэффициента трения, основанные на законах механики, определяющих соотношение между силой тяжести подвижного образца и углом наклона испытательной системы. Например, известен способ определения динамического коэффициента внешнего трения скольжения при наклоне двух расположенных друг на друге образцов, нижний из которых, имеющий форму диска, приводят во вращение вокруг своей оси и наклоняют относительно горизонта, удерживая верхний образец в том месте диска, где его линейная скорость направлена вверх по уклону, при этом динамический коэффициент трения определяют по текущему значению угла наклона φ в тот момент, когда верхний образец начинает соскальзывать вниз [патент РФ №2458336, G01N 19/02, опубл. 10.08.2012].

Недостатком этого способа определения коэффициента трения является необходимость больших габаритов приводящегося во вращение образца, что трудно обеспечить при исследовании некоторых материалов с особыми свойствами.

Известен также выбранный в качестве прототипа способ определения динамического коэффициента внешнего трения между двумя расположенными друг на друге образцами, нижний из которых имеет цилиндрическую или сферическую вогнутую рабочую поверхность. Поворачивая образцы относительно горизонтальной оси, измеряют угол наклона φ₁ относительно вертикали, при котором происходит соскальзывание верхнего образца, и угол φ₂, при котором соскальзывание образца завершается, по значениям углов φ₁ и φ₂, исходя из равенства работы, совершаемой силой трения при соскальзывании верхнего образца, сопутствующему изменению потенциальной энергии верхнего образца, меняющего положение по вертикали, рассчитывают динамический коэффициент внешнего трения как , где k - расчетный поправочный коэффициент, учитывающий несовпадение центра тяжести верхнего образца с рабочей поверхностью нижнего образца [патент РФ №2537745, G01N 19/02, опубл. 10.01.2015].

К числу недостатков способа относится необходимость использования, по крайней мере у одного из образцов, достаточно протяженной и обязательно криволинейной, с постоянным радиусом, рабочей поверхности, что усложняет технику эксперимента, а при наличии только плоских образцов исключает возможность его проведения. Помимо этого выбранный в качестве прототипа способ обладает систематической погрешностью, для компенсации которой требуются дополнительные действия по определению поправочного коэффициента.

Техническим результатом предлагаемого технического решения является возможность определения динамического коэффициента внешнего трения при ограниченных габаритах образцов одинаковой формы без измерения сил трения, путем использования принципа равенства между кинетической энергией образца, движущегося с определенной начальной скоростью, и работой силы трения, совершаемой в процессе относительного перемещения образца до полной его остановки.

Для достижения технического результата используют два образца, расположенных друг на друге, при этом нижний образец закрепляют в центре платформы, способной поворачиваться относительно горизонтальной оси подвески. Плоскую рабочую поверхность платформы располагают параллельно оси подвески, перпендикулярно плоскости, проходящей через ось подвески и геометрический центр рабочей поверхности платформы. Верхний образец свободно устанавливают на поверхности нижнего, отклоняют платформу с образцами от вертикального положения на некоторый угол θ и отпускают для свободного движения под действием силы тяжести по закону физического маятника. На пути движения платформы помещают упор, останавливающий ее вместе с закрепленным на ней нижним образцом в момент, когда платформа принимает нижнее положение. После остановки измеряют путь S, который по инерции проходит верхний образец по остановившейся в горизонтальном положении поверхности нижнего образца. Динамический коэффициент внешнего трения определяют по формуле

,

где θ - угол отклонения платформы от вертикального положения;

l - расстояние от центра тяжести верхнего образца до точки подвески платформы;

g - ускорение свободного падения;

Т - период колебаний платформы с образцами, определяемый в дополнительном опыте в процессе свободных колебаний, совершаемых ею без ограничения движения упором при отведении на такой же угол θ от вертикального положения.

С момента встречи платформы с препятствием и остановки нижнего образца верхний образец, двигаясь по инерции, проходит на поверхности нижнего некоторый путь, преодолевая силу трения, пропорциональную его весу и динамическому коэффициенту внешнего трения, и совершает работу, пропорциональную пройденному пути. Динамический коэффициент внешнего трения определяют из условия равенства кинетической энергии верхнего образца, движущегося в момент столкновения с известной скоростью, работе, которую производит, преодолевая силу трения, образец при перемещении после столкновения.

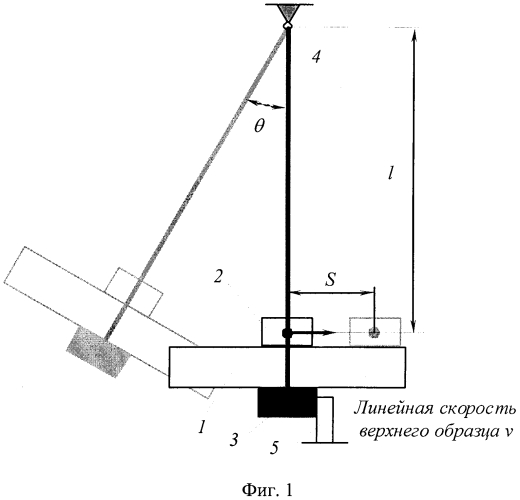
На фиг. 1 показана схема реализации предлагаемого способа экспериментального определения динамического коэффициента внешнего трения, объединенная со схемой действующих на образец усилий, где:

1 - нижний образец;

2 - верхний образец;

3 - платформа;

4 - ось подвески;

5 - упор.

Для определения динамического коэффициента внешнего трения используют два образца (фиг. 1), нижний 1 и верхний 2. Нижний образец 1 устанавливают и закрепляют на выполненной в виде физического маятника платформе 3, способной совершать свободные колебания относительно горизонтальной оси подвески 4. Рабочую поверхность платформы 3 располагают параллельно оси подвески 4 и перпендикулярно плоскости, проходящей через ось подвески 4 и геометрический центр рабочей поверхности платформы 3. На пути движения платформы 3 устанавливают жесткое препятствие в виде упора 5, способное остановить движение платформы 3 в ее нижнем положении. При отсутствии упора 5 платформа 3 может совершать колебательные движения относительно оси подвески 4 под действием собственного веса и веса установленных на ней образцов.

Определение динамического коэффициента внешнего трения производят в следующем порядке. Платформу 3 с нижним образцом 1 и верхним образцом 2 отклоняют от вертикального положения на некоторый фиксированный угол θ и отпускают, после чего она начинает свободное движение по закону гармонических колебаний. Предварительно на пути платформы 3 размещают упор 5, который останавливает ее движение в момент достижения нижнего положения, при котором рабочая поверхность нижнего образца 1 и вектор скорости верхнего образца 2 направлены горизонтально. К этому моменту движущаяся по закону физического маятника система приобретает некоторую угловую скорость ω, а линейная скорость верхнего образца 2, центр тяжести которого конструктивно находится на некотором расстоянии l от точки подвески 4, составит v=ωl. После остановки платформы 3 и закрепленного на ней нижнего образца 7 верхний образец 2, двигаясь по инерции, скользит по поверхности нижнего образца 1 и проходит некоторый путь S, зависящий от достигнутой скорости и величины динамического коэффициента трения. Если величина этого пути больше или меньше оптимального значения, обусловленного размерами образцов, опыт повторяют, изменяя скорость образцов вариацией угла θ между исходным и нижним положениями платформы 3. В конечном счете, определяют угол θ, при котором проходимый верхним образцом 2 путь S оптимален, и фиксируют значение пути, соответствующее данному углу.

Проходя по инерции путь S, верхний образец 2 совершает работу, обусловленную наличием силы трения F_тр. В момент столкновения платформы 3 с упором 5 рабочая поверхность нижнего образца 1 и вектор скорости верхнего образца 2 направлены горизонтально, поэтому силу трения можно определить как

F_тр=Mgf_дин,

где g - ускорение свободного падения; f_дин - динамический коэффициент трения.

Работа, которая совершается верхним образцом 2 в процессе скольжения до полной остановки, находится по формуле

A=F_тр·S=Mgf_дин,

где S - путь, пройденный верхним образцом 2.

Исходя из закона сохранения энергии совершенная работа и начальная кинетическая энергия верхнего образца 2 равны между собой. Кинетическая энергия верхнего образа 2, имеющего массу М, равна

Таким образом,

,

что дает основание записать выражение для определения динамического коэффициента трения в виде

Для определения динамического коэффициента трения по формуле (1) используется величина линейной скорости v верхнего образца 2, связь которой с параметрами колебательного движения платформы 3 определяется теорией гармонических колебаний. При небольших углах колебания θ (менее 15°) с погрешностью менее 0,5%, допустимой при определении коэффициента трения, движение платформы 3 описывается уравнением [Джанколи Д. Физика: В 2-х т. Т. 1: Пер. с англ. - М.: Мир, 1989, с. 410]

,

где θ_т - текущее угловое отклонение оси маятника от вертикального положения; θ - максимальное угловое отклонение оси маятника; t - текущее время процесса, прошедшее от начала колебаний; Т - период колебаний; φ - некоторая начальная фаза колебаний.

Угловая скорость ω колеблющегося маятника определяется как производная текущего угла поворота θ_т

.

Как следует из полученной формулы, угловая скорость системы также изменяется по закону гармонических колебаний, достигая максимального по абсолютной величине значения при нижнем положении платформы 3 с образцами, т.е. при . Таким образом, максимальная угловая скорость системы в нижнем положении платформы составляет

С помощью полученной формулы находят максимальную линейную скорость центра тяжести верхнего образца 2

где l - расстояние от оси подвески 4, являющейся центром поворота, до центра тяжести верхнего образца 2, определяемое конструктивно.

Использованием полученного выражения позволяет, не производя сложное измерение скорости верхнего образца 2 в момент соударения, определять ее простым расчетно-экспериментальным путем. Для этого проводят дополнительный опыт по определению периода колебаний Т, во время которого упор 5 убирают, а платформу 3 с образцами приводят в колебательное движение из того же исходного положения с углом отклонения θ. Период колебаний Т находят, определяя при помощи хронометража продолжительность одного цикла колебаний. Для повышения точности результата определяют суммарную продолжительность t некоторого числа n полных циклов колебаний, а величину периода колебаний находят по формуле

.

После нахождения значения Т с использованием формулы (2) определяют скорость верхнего образца 2 в момент столкновения. С учетом формул (1) и (2) определяют динамический коэффициент внешнего трения

.

Для расчета коэффициента внешнего трения величину исходного угла отклонения платформы θ определяют в радианах, период колебаний платформы с образцами Т - в секундах, величину смещения S верхнего образца 2 по поверхности нижнего образца 1 и расстояние l от точки подвески 4 платформы 5 до центра тяжести верхнего образца 2 - в метрах, величину ускорения свободного падения принимают равной g=9,8 м/с².

Предлагаемый способ определения динамического коэффициента внешнего трения, реализуемый при малых скоростях относительно перемещения, наиболее целесообразен для статических систем с крепежными элементами и другими неподвижными соединениями, основанными на использовании сил трении, в которых велика вероятность нарушения относительной неподвижности вследствие внешних вибраций или ударных нагрузок и надежность системы должна оцениваться с учетом динамического коэффициента трения, который у большинства материалов уступает по величине статическому. Достоинством способа является возможность его реализации с использованием образцов весьма малых размеров, таких же, как и при определении статического коэффициента внешнего трения. Используемая для реализации способа оснастка универсальна, с ее помощью может определяться не только динамический, но и статический коэффициент внешнего трения. Для этого платформу 3 с образцами постепенно отклоняют от вертикального положения, увеличивая угол θ, до того момента, при котором произойдет соскальзывание верхнего образца 2, а по определенному в момент соскальзывания верхнего образца 2 предельному углу рассчитывают статический коэффициент внешнего трения по известной формуле.

Способ определения динамического коэффициента внешнего трения при относительном перемещении двух образцов, расположенных друг на друге, отличающийся тем, что нижний образец закрепляют в центре платформы, способной поворачиваться относительно горизонтальной оси подвески, плоскую рабочую поверхность платформы располагают перпендикулярно плоскости, проходящей через ось подвески и геометрический центр рабочей поверхности платформы, верхний образец свободно устанавливают на поверхности нижнего, отклоняют платформу с образцами от вертикального положения на угол θ и отпускают для свободного движения под действием силы тяжести по закону физического маятника, на пути движения платформы помещают упор, останавливающий ее вместе с нижним образцом в нижнем горизонтальном положении, измеряют путь S, который проходит по инерции верхний образец, и определяют динамический коэффициент внешнего трения по формуле где θ - угол отклонения платформы от вертикального положения;l - расстояние от центра тяжести верхнего образца до точки подвески платформы;g - ускорение свободного падения;Т - период колебаний платформы с образцами, определяемый в дополнительном опыте в процессе свободных колебаний, совершаемых ею без ограничения движения упором при отведении на такой же угол θ от вертикального положения.