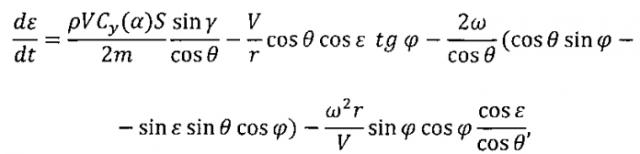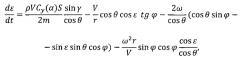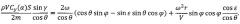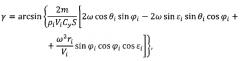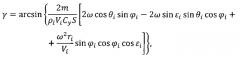Способ управления движением космического аппарата при посадке в заданную область поверхности планеты

Способ управления движением космического аппарата при посадке в заданную область поверхности планеты

Иллюстрации

Показать все

Реферат

Изобретение относится к космонавтике, в частности к области управления спуском космического аппарата (КА), осуществляющего изменение аэродинамического качества в процессе движения в атмосфере и обеспечивающего посадку КА в заданную область поверхности планеты.

Обеспечение высокоточной посадки на поверхность Земли и планет является одной из важных и сложных задач управления КА, во многом определяющей успешную реализацию космических миссий.

Известен ряд способов управления КА аэродинамическим качеством при посадке на поверхность Земли и планет. Так, достаточно простым и неоднократно реализуемым на практике с использованием КА серий «Союз» и «Прогресс» является способ, описанный в книге «Навигационное обеспечение полета орбитального комплекса «Салют-6» - «Союз» - «Прогресс» / Под ред. Петрова Б.Н. и Бажинова И.К. М.: Наука, 1985 - [1], стр. 273-278. Способ предусматривает предварительное проведение ракетодинамической коррекции с целью обеспечения прохождения трассы КА на витке спуска через расчетную точку посадки, определение момента схода КА с орбиты путем реализации импульса характеристической скорости на торможение КА, перевод КА на траекторию спуска, обеспечение прохождения спускаемым аппаратом плотных слоев атмосферы и реализацию посадки в заданном районе. Точность посадки при реализации данного способа в боковом направлении обеспечивается точностью проведения ракетодинамической коррекции «прохождения», а в продольном направлении - точностью выбора момента схода КА с орбиты.

Данный способ имеет ряд недостатков. Во-первых, он предполагает необходимость проведения ракетодинамической коррекции орбитального движения КА, что требует дополнительных затрат топлива и снижает оперативность спуска аппарата в заданный район посадки. Во-вторых, способ не предусматривает проведения оперативных коррекций траекторий спуска в связи с воздействием на динамику полета КА возмущающих факторов и наличием погрешностей в отработке управляющих функций, что может привести к снижению точности посадки КА. Кроме того, управленческие операции, характерные данному способу, не могут быть реализованы при спуске на поверхность планеты при подлете КА с межпланетных гиперболических орбит.

Известен способ управления, описанный в работе Иванов Н.М., Мартынов А.И. «Управление движением космических аппаратов в атмосфере Марса». Москва, «Наука», 1977 - [2], стр. 224-237, предусматривающий двухразовое переключение эффективного аэродинамического качества K_эф в соответствии с программой:

K_эф:K_бcosγ^*→K_бcos(π-γ^*)→K_бcosγ^*,

где K_б - балансировочное аэродинамическое качество, определяемое углом атаки α;

γ^* - угол крена, обеспечивающий боковой маневр КА.

Следует отметить, что используемые в настоящее время спускаемые аппараты, а также проектируемые КА для реализации перспективных космических миссий располагают аэродинамическим качеством K_б, не превышающим 2,5-3.

При осуществлении этого способа выбором моментов переключения K_эф обеспечивается заданная продольная дальность спуска КА в атмосфере, а выбором значения γ^* - заданная боковая дальность.

Достоинством способа является то, что он не предполагает проведения дополнительной ракетодинамической коррекции траектории движения КА, а также предусматривает возможность компенсации влияния возмущающих факторов на дальность спуска КА за счет изменения моментов переключения аэродинамического качества.

Основной недостаток данного способа заключается в том, что даже при выборе оптимального значения угла γ^* из класса постоянных функций, боковая дальность спуска будет существенно меньше максимально возможных значений L_бmax, что ограничивает возможность посадки КА в районах поверхности планеты, значительно удаленных от плоскости входа КА в атмосферу. Другим недостатком способа является отсутствие возможности оперативной коррекции дальности полета КА в боковом направлении, т.к. в рамках реализации этого способа не предусматривается проведение оперативной коррекции угла γ^*. Это может привести к большим отклонениям точки посадки от заданной.

Наиболее близким по технической сущности к заявляемому способу управления движением космического аппарата при посадке в заданную область поверхности планеты, использующему управление аэродинамическим качеством является способ, описанный в работе Соколов Н.Л., Цыбульский Г.А. Исследование по оптимизации проектно-баллистических параметров комплекса скорой помощи на базе межконтинентальных баллистических ракет. Космические исследования, 1996, т. 34, №3 - [3], стр. 325-331, 328. Он заключается в осуществлении входа космического аппарата в атмосферу планеты с углом атаки α, соответствующим максимальному значению аэродинамического качества K_max; в измерении текущих значений координат движения космического аппарата в моменты времени t_i, где i=1, 2, 3, …, n, в процессе спуска в атмосфере, а именно V_i - скорости полета, θ_i - угла наклона вектора скорости космического аппарата к местному горизонту, ε_i - угла между проекцией вектора скорости космического аппарата на местный горизонт и местной параллелью, r_i - расстояния между центром планеты и центром масс космического аппарата, φ_i и λ_i - планетоцентрические широты и долготы подспутниковой точки космического аппарата, ρ_i - плотности атмосферы на высоте полета космического аппарата; в определении η - угла между проекцией вектора скорости космического аппарата на местный горизонт и вертикальной плоскостью входа аппарата в атмосферу; ψ - углового расстояния между двумя точками на земной сфере - подспутниковой точкой космического аппарата и точкой пересечения двух плоскостей большого круга, одна из которых является плоскостью входа космического аппарата в атмосферу, а другая перпендикулярна к ней и проходит через подспутниковую точку. При этом угол крена γ изменяется в соответствии с формулой Кутищева, обеспечивающей максимизацию боковой дальности полета КА.

, , 0<K_б≤3,

где η - угол между проекцией вектора скорости КА на местный горизонт и вертикальной плоскостью входа аппарата в атмосферу;

ψ - угловое расстояние между двумя точками на земной сфере - подспутниковой точкой космического аппарата и точкой пересечения двух плоскостей большого круга, одна из которых является плоскостью входа космического аппарата в атмосферу, а другая перпендикулярна к ней и проходит через подспутниковую точку;

K_б - балансировочное аэродинамическое качество, определяемое углом атаки α.

Как было отмечено, создаваемые КА для зондирования Земли и других планет Солнечной системы будут обладать аэродинамическим качеством, не превышающим 2,5-3.

Данный способ управления КА выбран в качестве прототипа, поскольку ему присуща совокупность признаков, наиболее близкая к совокупности существенных признаков изобретения. Способ-прототип позволяет значительно расширить зону маневра КА в атмосфере в боковом направлении по сравнению со способами-аналогами [1, 2]. В предельном случае при выборе угла α, соответствующего максимальному значению аэродинамического качества K_max, достигается абсолютный максимум боковой дальности L_бmax. Это принципиально позволяет совершить посадку КА в максимально широком диапазоне удаленности от плоскости входа КА в атмосферу. При этом точность посадки КА в заданную область поверхности планеты обеспечивается рациональным выбором и оперативной коррекцией угла атаки α и, соответственно, аэродинамического качества КА K_б.

Вместе с тем способ-прототип имеет существенные недостатки. Во-первых, в рамках реализации данного способа не может быть обеспечена одновременная коррекция отклонений по продольной и боковой дальностям на заключительном этапе спуска, что делает практически невозможным осуществление высокоточной посадки в заданную точку поверхности планеты. Во-вторых, с помощью данного способа принципиально отсутствует возможность компенсации кориолисовых и переносных сил, возникающих в связи с вращением планеты и зависящих от наклонений орбиты входа КА в атмосферу и планетоцентрических широт подспутниковых точек КА. В-третьих, при определении расчетного значения управляющего параметра α требуется проведение итерационного вычислительного процесса, что сопряжено с большой продолжительностью времени расчетов и может снизить оперативность управления при решении этой задачи в бортовом исполнении. В связи с этим представляется целесообразным разработка и использование безитерационных вычислительных алгоритмов для определения управляющих параметров движения КА.

Для достижения технического результата изобретения - точной посадки КА на полигоны малых размеров - разработан способ управления движением космического аппарата при посадке в заданную область поверхности планеты.

Сущность способа заключается в следующем.

Вся траектория спуска делится на два условных участка (см. фиг. 1). На первом участке, начинающемся от входа КА в атмосферу (1), с помощью управления углом крена (3) осуществляется интенсивный разворот аппарата по курсу и обеспечивается такое положение КА, при котором вектор его скорости будет находиться в вертикальной плоскости (4), проходящей через заданную точку посадки. На втором условном участке осуществляется полет КА в сформированной вертикальной плоскости, где путем управления балансировочным аэродинамическим качеством (5) обеспечивается требуемая продольная дальность спуска и посадка аппарата в заданную точку (6). Для рассматриваемого примера проекция трассы полета пересекает экватор (2).

На первом участке траектории спуска осуществляется управление углом крена γ КА, максимизирующим его боковую дальность при спуске. Такое управление известно, как из описания прототипа, так и из других источников информации, например, Шкадов Л.М., Буханова Р.С., Илларионов В.Ф., Плохих В.П. Механика оптимального пространственного движения ЛА в атмосфере. М.: Машиностроение. 1972. - [4], стр. 61-82, 219.

, , 0<K_б≤3,

где η - угол между проекцией вектора скорости КА на местный горизонт и вертикальной плоскостью входа аппарата в атмосферу;

ψ - угловое расстояние между двумя точками на земной сфере - подспутниковой точкой космического аппарата и точкой пересечения двух плоскостей большого круга, одна из которых является плоскостью входа космического аппарата в атмосферу, а другая перпендикулярна к ней и проходит через подспутниковую точку;

K_б - балансировочное аэродинамическое качество, определяемое углом атаки α, 0<K_б≤3.

Условием завершения управления КА на первом участке, т.е. условием достижения факта нахождения вектора скорости КА в вертикальной плоскости, проходящей через заданную точку посадки, будет являться обеспечение равенства между текущим наклонением плоскости орбиты аппарата i_т и наклонения условной орбиты i_усл, проходящей через подспутниковую точку КА и точку посадки.

Текущие значения i_т на первом участке полета непрерывно определяют по известной формуле, связывающей между собой наклонение орбиты, угол между проекцией вектора скорости космического аппарата на местный горизонт и местной параллелью и планетоцентрическую широту подспутниковой точки космического аппарата:

i_т=arccos(cosε_i·cosφ_i),

где ε_i - угол между проекцией вектора скорости космического аппарата на местный горизонт и местной параллелью на i-м интервале измерений;

φ_i - планетоцентрическая широта подспутниковой точки космического аппарата на i-м интервале измерений, i=1, 2, 3, …, n.

На фиг. 2 представлены два сферических треугольника, анализ которых позволяет определить наклонение условной орбиты i_усл (8). Первый сферический треугольник образуется тремя дугами большого круга со следующими подспутниковыми точками: точкой пересечения плоскости условной орбиты и плоскости экватора (7), подспутниковой точкой текущего положения космического аппарата (10) и точкой пересечения полярной плоскости, проходящей через подспутниковую точку текущего положения КА и плоскости экватора (12). Второй сферический треугольник образуется тремя дугами большого круга со следующими подспутниковыми точками: точкой пересечения плоскости условной орбиты и плоскости экватора (7), точкой посадки космического аппарата (13) и точкой пересечения полярной плоскости, проходящей через точку посадки КА и плоскости экватора (15). Для определения наклонения i_усл использовались следующие исходные данные: разность планетоцентрических долгот текущего положения КА λ_i и пересечения плоскостей условной орбиты и экватора (9), планетоцентрическая широта текущего положения КA φ_i (11), планетоцентрические широта φ_п (13) и долгота λ_п (15). Введем обозначения: δ - дуга, принадлежащая анализированной условной плоскости большого круга (16), образованная точками (10) и (13); σ - дуга, принадлежащая анализированной условной плоскости большого круга (16), образованная точками (7) и (13).

Дуга δ определяется по известной формуле теоремы косинусов сферической геометрии:

δ=arccos[sinφ_isinφ_п+cosφ_icosφ_пcos(λ_п-λ_i)],

где φ_п - планетоцентрическая широта точки посадки космического аппарата;

λ_п - планетоцентрическая долгота точки посадки космического аппарата;

φ_i - планетоцентрическая широта подспутниковой точки космического аппарата на i-м интервале измерений;

λ_i - планетоцентрическая долгота подспутниковой точки космического аппарата на i-м интервале измерений, i=1, 2, 3, …, n.

Для описанных двух сферических треугольников с использованием известных формул теоремы синусов запишем два уравнения:

, .

Решая эти два уравнения с двумя неизвестными σ и i_усл, получим:

,

.

По достижении условия i_т=i_усл осуществляется полет КА в плоскости, проходящей через точку посадки. Следует отметить, что действующие на КА кориолисовы и переносные силы, вызванные вращением планеты, приводят к изменению плоскости движения аппарата. Поэтому для поддержания постоянной плоскости движения КА необходимо осуществлять компенсацию этих сил с помощью управления аэродинамическими силами. Проанализируем дифференциальное уравнение, описывающее изменение угла между проекцией вектора скорости космического аппарата на местный горизонт и местной параллелью:

где V - скорость КА;

θ - угол наклона скорости к местному горизонту;

ε - угол между проекцией скорости на местный горизонт и местной параллелью;

r - расстояние между центром планеты и центром масс космического аппарата;

φ - планетоцентрическая широта подспутниковой точки КА;

m - масса КА;

ρ - плотность атмосферы на высоте полета КА;

С_y - аэродинамический коэффициент лобового сопротивления КА;

γ - угол крена КА;

ω - угловая скорость вращения планеты;

α - угол атаки КА;

S - площадь миделева сечения КА.

Из рассмотрения этого уравнения следует, что для обеспечения компенсации кориолисовых и переносных сил аэродинамическими должно выполняться условие:

Это условие выполняется при следующем управлении углом крена:

где m - масса космического аппарата;

С_y - аэродинамический коэффициент подъемной силы космического аппарата;

S - площадь миделева сечения космического аппарата;

ω - угловая скорость вращения планеты;

V_i - скорость полета космического аппарата на i-м интервале измерений;

θ_i - угол наклона вектора скорости космического аппарата к местному горизонту на i-м интервале измерений;

ε_i - угол между проекцией вектора скорости космического аппарата на местный горизонт и местной параллелью на i-м интервале измерений;

r_i - расстояние между центром планеты и центром масс космического аппарата на i-м интервале измерений;

φ_i - планетоцентрическая широта подспутниковой точки космического аппарата на i-м интервале измерений, i=1, 2, 3, …, n.

На втором участке полета осуществляется движение в плоскости орбиты, проходящей через заданную точку посадки КА. На этом участке реализуется управление продольной дальностью спуска с помощью изменения балансировочного аэродинамического качества, что обеспечивает посадку КА в заданную точку. При этом непрерывно осуществляются вычисления прогнозируемой дальности на заключительном участке спуска L₁ при движении аппарата с постоянным значением аэродинамического качества, которое КА принимает в текущий момент времени t_i.

Расчет дальности L₁ проводится с использованием известных дифференциальных уравнений движения КА:

, ,

где h - высота полета КА;

L - продольная дальность полета КА;

V - скорость полета КА;

θ - угол наклона вектора скорости космического аппарата к местному горизонту;

t - время полета КА.

Поделив второе уравнение на первое, получим:

.

Для его аналитического интегрирования введем допущение: будем считать угол θ кусочно-постоянным на завершающем участке полета и равным среднему арифметическому значению между текущей величиной θ_i и установившимся значением, принимаемым в конце участка аэродинамического торможения θ_уст (зависимость для расчета θ_уст обосновывается в книге - [2], с. 149-151:

, ,

где K_б - балансировочное аэродинамическое качество, определяемое углом атаки α КА;

γ - угол крена КА.

С учетом представленных уравнений зависимость для расчета дальности L₁ будет иметь вид:

.

Следует отметить, что введенное допущение не приводит к значительным погрешностям в определении дальности L₁, т.к. расчетные погрешности не носят системного характера ввиду непрерывного пересчета дальности полета КА.

Рассчитанную дальность пуска L₁ непрерывно сравнивают с дальностью между текущей подспутниковой точкой движения КА и заданной точкой посадки L₂. Эта дальность вычисляется в соответствии с известной формулой теоремы косинусов сферической геометрии:

L₂=Rarccos[sinφ_isinφ_п+cosφ_icosφ_пcos(λ_п-λ_i)], h_i=r_i-R,

где φ_п - планетоцентрическая широта точки посадки космического аппарата;

λ_п - планетоцентрическая долгота точки посадки космического аппарата;

φ_i - планетоцентрическая широта подспутниковой точки космического аппарата на i-м интервале измерений;

λ_i - планетоцентрическая долгота подспутниковой точки космического аппарата на i-м интервале измерений;

h_i - высота полета космического аппарата на i-м интервале измерений;

r_i - расстояние между центром планеты и центром масс космического аппарата на i-м интервале измерений, i=1, 2, 3, …, n;

R - средний радиус планеты.

Очевидно, что при значительном удалении КА от заданной точки посадки дальность L₂ будет превышать дальность L₁. При таком условии полет КА продолжает осуществляться с углом атаки α, соответствующим максимальному значению балансировочного аэродинамического качества K_б, что обеспечивает максимальную продолжительность траектории спуска. В процессе полета КА дальность L₂ будет монотонно уменьшаться и, начиная с некоторого момента времени, будет равной дальности L₁. В связи с этим, при продолжении полета с максимальным значением балансировочного аэродинамического качества K_б возникает опасность перелета космическим аппаратом заданной точки посадки. Во избежание этого негативного фактора обеспечивается снижение дальности L₂ за счет уменьшения балансировочного аэродинамического качества K_б. Обязательным условием уменьшения L₂ является увеличение крутизны траектории полета, т.е. увеличение абсолютного среднего значения угла наклона вектора скорости к местному горизонту θ_ср, которое определяется из условия:

, ,

где θ_тр - требуемое значение угла наклона вектора скорости космического аппарата к местному горизонту для обеспечения необходимой крутизны траектории движения;

θ_уст - установившееся значение угла наклона вектора скорости космического аппарата к местному горизонту.

Решая данное уравнение, получим зависимость для расчета требуемого угла θ_тр:

.

Для определения программы изменения балансировочного аэродинамического качества K_б, при которой обеспечивается точная посадка КА на поверхность планеты, используем известные дифференциальные уравнения, описанные в работе Соколов Н.Л. «Приближенный аналитический метод расчета пространственных маневров космического аппарата в атмосфере». Космические исследования. 1988, т. 26, №2 - [5], с. 209-212:

, ,

где V - скорость полета;

ρ - плотность атмосферы на высоте полета КА;

θ - угол наклона вектора скорости космического аппарата к местному горизонту;

K_б - балансировочное аэродинамическое качество, определяемое углом атаки α КА;

γ - угол крена КА;

Р_x - приведенная нагрузка на лобовую поверхность КА;

β - логарифмический коэффициент изменения плотности атмосферы от высоты;

М₁ - кусочно-постоянный коэффициент, учитываемый при расчетах траекторий движения космического аппарата;

t - время полета КА.

Поделив первое уравнение на второе, запишем следующее соотношение:

Для получения зависимости, характеризующей изменения балансировочного аэродинамического качества K_б на заключительном этапе полета, проинтегрируем это уравнение в пределах от текущего состояния движения КА до точки посадки. Текущее состояние характеризуется известным значением плотности атмосферы ρ_i на высоте полета КА на i-м интервале измерений и требуемой величиной угла наклона вектора скорости к местному горизонту θ_тр, при котором обеспечивается необходимая крутизна завершающегося участка спуска. Для конечного состояния полета (точка посадки) известны плотность атмосферы на поверхности планеты ρ_п и установившееся значение угла наклона вектора скорости космического аппарата к местному горизонту θ_уст.

После интегрирования этого уравнения и его преобразования получим соотношение для определения значения K_б в зависимости от требуемой величины угла θ_тр:

Δρ_i=ρ_i-ρ_п,

где ρ_i - плотность атмосферы на высоте полета космического аппарата на i-м интервале измерений, i=1, 2, 3, …, n;

Р_х - приведенная нагрузка на лобовую поверхность космического аппарата;

β - логарифмический коэффициент изменения плотности атмосферы от высоты;

γ - угол крена КА;

М₁ - кусочно-постоянный коэффициент, учитываемый при расчетах траекторий движения космического аппарата;

ρ_п - плотность атмосферы на поверхности планеты.

Итак, управление КА на заключительном участке спуска состоит в следующем: на каждом интервале измерения траекторных параметров пересчитывают значения дальностей L₁ и L₂. При L₁>L₂ определяется требуемое значение угла наклона вектора скорости КА к местному горизонту θ_тр, при котором обеспечивается необходимая крутизна траектории для осуществления точной посадки аппарата на поверхность планеты. В зависимости от величины этого угла θ_тр рассчитывается значение балансировочного аэродинамического качества K_б. Такое управление с пошаговой коррекцией величины K_б осуществляется до посадки КА на поверхность планеты.

Таким образом, предложенный способ управления обладает рядом преимуществ по сравнению с аналогами и прототипом. Реализация данного способа позволяет повысить точность посадки КА на поверхность планеты за счет использования рациональной программы управления балансировочным аэродинамическим качеством и углом крена. Так, на начальном участке полета реализуется точное выведение КА в плоскость, проходящую через точку посадки. На заключительном участке осуществляется удержание движения КА в этой плоскости, что исключает возникновение боковых отклонений точки посадки от заданной, а также обеспечивается непрерывное управление аэродинамическим качеством, что позволяет реализовать требуемые значения продольной дальности спуска. Кроме того, разработанные вычислительные зависимости, используемые при осуществлении заявляемого способа, являются безитерационными, что делает возможным и эффективным в бортовом исполнении.

Технический результат изобретения заключается в повышении точности посадки КА на полигоны малых размеров, что позволяет повысить надежность и оперативность реализации космических миссий, снизить требования к наземной инфраструктуре управления и минимизировать затраты на ее использование. Это особенно важно при существенном планируемом расширении орбитальных группировок КА, большое число которых предполагает осуществление посадки на полигоны малых размеров. Кроме того, необходимость высокоточной посадки является актуальной для выполнения космических миссий, предусматривающих спуск в атмосферах Марса и Венеры, где имеет место неравномерность поверхности указанных планет. Полученные результаты численных расчетов показали, что при использовании заявляемого способа отклонения точки посадки от заданной существенно меньше, чем для способов-аналогов и способа-прототипа, и не превышают ~0,5 км при спуске на поверхность Земли и ~1-2 км при спуске в атмосфере Марса. При этом не учитывалась неточность знания параметров нижних слоев атмосферы Марса, а также возможные случайные возмущающие факторы.

Указанный технический результат достигается за счет использования рациональных программ управления балансировочным аэродинамическим качеством и углом крена, а также за счет установки на борту космического аппарата высокотехнологичных систем управления, использующих безитерационные бортовые вычислительные алгоритмы, что позволяет в масштабе времени, близком к реальному, обеспечить управление КА в соответствии с разработанными алгоритмами.

Заявляемый способ управления движением космического аппарата при посадке в заданную область поверхности планеты поясняется следующими фигурами.

На фиг. 1 представлена проекция трассы управляемого полета космического аппарата на развертку поверхности планеты. Приняты следующие обозначения:

1 - подспутниковая точка положения КА в момент его входа в атмосферу;

2 - плоскость экватора;

3 - трасса начального участка полета, где осуществляется управление КА углом крена и выведение в плоскость, проходящую через точку посадки;

4 - подспутниковая точка положения КА в момент его выведения в плоскость, проходящую через точку посадки;

5 - трасса заключительного этапа полета, где осуществляется управление балансировочным аэродинамическим качеством с целью обеспечения заданной продольной дальности полета КА;

6 - точка посадки КА на поверхность планеты.

На фиг. 2 представлены сферические треугольники для обоснования определения текущих значений наклонения условной орбиты i_усл, проходящей через подспутниковую точку текущего положения КА и точку посадки. Приняты следующие обозначения:

7 - точка пересечения плоскости условной орбиты и плоскости экватора;

8 - наклонение условной орбиты i_усл;

9 - дуга, принадлежащая плоскости экватора, определяемая как разность между планетоцентрической долготой подспутниковой точки положения КА и планетоцентрической долготой пересечения плоскостей условной орбиты и экватора;

10 - подспутниковая точка текущего положения космического аппарата;

11 - планетоцентрическая широта текущего положения КА;

12 - точка пересечения полярной плоскости, проходящей через подспутниковую точку текущего положения КА и плоскостью экватора;

13 - точка посадки космического аппарата;

14 - планетоцентрическая широта точки посадки КА;

15 - точка пересечения полярной плоскости, проходящей через точку посадки КА и плоскостью экватора;

16 - условная плоскость орбиты, образованная подспутниковой точкой текущего положения КА и точкой посадки.

На фиг. 2 условная орбита определяется позицией 16. Условная орбита - орбита, непрерывно меняющаяся в процессе полета в зависимости от текущего положения подспутниковой точки космического аппарата. Условная орбита вводится для установления факта нахождения вектора скорости космического аппарата в вертикальной плоскости, проходящей через заданную точку посадки, что является признаком завершения процесса управления углом крена.

Связь «условной орбиты» с «плоскостью входа» заключается в их совпадении только в начальный момент движения космического аппарата в атмосфере. Связь «условной орбиты» с «плоскостью 16 большого круга» заключается в том, что на фиг. 2 плоскость 16 в текущий момент времени играет роль «условной орбиты». При этом на фиг. 1, где представлена проекция трассы управляемого полета космического аппарата на развертке поверхности планеты, «условная орбита» не отображена.

Ожидаемая эффективность использования предлагаемого способа управления по сравнению, например, со способом-прототипом состоит в существенном уменьшении отклонений точки посадки КА на поверхность планет. Так, при спуске в атмосфере Земли отклонения не превышают 0,5 км, а при спуске в атмосфере Марса ~1-2 км.

Покажем возможность осуществления изобретения, т.е. возможность его промышленного применения.

Как известно, спуск в атмосферах Земли и планет является завершающим и наиболее динамичным этапом космических экспедиций. Его успешная реализация зависит от ряда различных факторов, в том числе и от обеспечения высокоточной посадки в заданную область поверхности планет, что во многом обеспечивает эффективное выполнение программ полета в целом. Вышеперечисленное обуславливает актуальность разработки способа управления движением космического аппарата при посадке в заданную область поверхности планеты. Использование данного способа при проектировании космических миссий ближнего и дальнего космоса позволит повысить эффективность их реализации.

Что касается технических средств, обеспечивающих управление движением КА при посадке в заданную область поверхности планеты, то они известны - см., например, работу - [2], стр. 270-279, и при необходимости приведенную в ней многочисленную библиографию.

Способ управления движением космического аппарата при посадке в заданную область поверхности планеты, заключающийся в осуществлении входа космического аппарата в атмосферу планеты с углом атаки α, соответствующим максимальному значению аэродинамического качества K_max; в измерении текущих значений координат движения космического аппарата в моменты времени t_i, где i=1, 2, 3, …, n, в процессе спуска в атмосфере, а именно V_i - скорости полета, θ_i - угла наклона вектора скорости космического аппарата к местному горизонту, ε_i - угла между проекцией вектора скорости космического аппарата на местный горизонт и местной параллелью, r_i - расстояния между центром планеты и центром масс космического аппарата, φ_i и λ_i - планетоцентрических широты и долготы подспутниковой точки космического аппарата, ρ_i - плотности атмосферы на высоте полета космического аппарата; в определении η - угла между проекцией вектора скорости космического аппарата на местный горизонт и вертикальной плоскостью входа аппарата в атмосферу, ψ - углового расстояния между двумя точками на земной сфере - подспутниковой точкой космического аппарата и точкой пересечения двух плоскостей большого круга, одна из которых является плоскостью входа космического аппарата в атмосферу, а другая перпендикулярна к ней и проходит через подспутниковую точку, в изменении угла крена γ космического аппарата, максимизирующего его боковую дальность при спуске, отличающийся тем, что непрерывно определяют текущие значения наклонения плоскости орбиты космического аппарата i_т в соответствии с зависимостью: i _т = arccos(cosε _i·cosφ _i),где ε _i - угол между проекцией вектора скорости космического аппарата на местный горизонт и местной параллелью на i-м интервале измерений;φ_i - планетоцентрическая широта подспутниковой точки космического аппарата на i-м интервале измерений, i=1, 2, 3, …, n,вычисляют текущее значение наклонения условной орбиты i_усл, проходящей через текущую подспутниковую точку космического аппарата и точку посадки в соответствии с зависимостями: δ=arccos[sinφ_isinφ_п+cosφ_icosφ_gcos(λ_п-λ_i)],где φ_п - планетоцентрическая широта точки посадки космического аппарата;λ_п - планетоцентрическая долгота точки посадки космического аппарата;φ_i - планетоцентрическая широта подспутниковой точки космического аппарата на i-м интервале измерений;λ_i - планетоцентрическая долгота подспутниковой точки космического аппарата на i-м интервале измерений, i=1, 2, 3, …, n,в процессе разворота космического аппарата в горизонтальной плоскости полета непрерывно осуществляют сравнение вычисленных значений наклонений i_т и i_усл; по достижении условия:i_т=i_усл,где i_т - текущее значение наклонения плоскости орбиты космического аппарата;i_усл - текущее значение наклонения условной орбиты, проходящей через текущую подспутниковую точку космического аппарата и точку посадки,в процессе полета космического аппарата на завершающем участке спуска устанавливают углы крена γ, вычисленные в соответствии с зависимостью: где m - масса космического аппарата;С_y - аэродинамический коэффициент подъемной силы космического аппарата;S - площадь миделева сечения космического аппарата;ω - угловая скорость вращения планеты;V_i - скорость полета космического аппарата на i-м интервале измерений;θ_i - угол наклона вектора скорости космического аппарата к местному горизонту на i-м интервале измерений;ε_i - угол между проекцией вектора скорости космического аппарата на местный горизонт и местной параллелью на i-м интервале измерений;r_i - расстояние между центром планеты и центром масс космического аппарата на i-м интервале измерений;φ_i - планетоцентрическая широта подспутниковой точки космического аппарата на i-м интервале измерений, i=1, 2, 3, …, n,при этом непрерывно осуществляют вычисления прогнозируемой дальности полета космического аппарата на заключительном участке спуска L₁ и дальность между текущей подспутниковой точкой полета космического аппарата и заданной точкой посадки в соответствии с зависимостями: L₂ = Rarccos[sinφ_isinφ_п+cosφ_icosφ_пcos(λ_п-λ_i)], h_i