Способ построения диаграммы предельных деформаций листового материала

Способ построения диаграммы предельных деформаций листового материала

Иллюстрации

Показать все

Реферат

Изобретение относится к области листовой штамповки, в частности к исследованию механических свойств листовых материалов для оценки их штампуемости как возможности получения пластических деформаций без разрушения листовой заготовки, полученной из листового материала, на формоизменяющих операциях листовой штамповки, а также для использования в CAD/CAE-системах (Computer-Aided-Design/Computer-Aided-Engineering-системах) при компьютерном моделировании и проектировании формоизменяющих операций листовой штамповки перед их внедрением в автомобильной и других отраслях промышленности.

Известен патент 2134872 G01N 3/28 от 20.08.1999 (Способ построения диаграммы предельных деформаций и устройство для его реализации), в котором блок, собранный из образца с прижимом и матрицы, устанавливают в контейнере и деформируют стальной дробью диаметром 0,5-1,5 мм с помощью пуансона в силовой установке. Недостатком известного аналога и прототипа является то, что требуется использование специального дорогостоящего оборудования и длительный срок проведения испытаний и построения диаграммы предельных деформаций (ДПД).

Задача изобретения состоит в снижении трудоемкости, сроков и стоимости построения ДПД листовых материалов.

Задачу решают следующим образом. Для определения вероятности разрушения листовой заготовки на формоизменяющих операциях листовой штамповки, таких как вытяжка или формовка сложных деталей типа коробчатых или кузовных, растяжение или обтяжка листов, используют два критерия:

1) разрушение в результате деформаций: на каждом этапе деформирования листовой заготовки точки с координатами наименьшей главной деформации ε₂ и наибольшей главной деформации ε₁ для всех элементов листовой заготовки должны располагаться ниже ДПД листового материала ε₁=f(ε₂) с определенным запасом P_d пластичности по деформациям; при заданной абсциссе ε₂ принимают ординату ε₁ до ДПД за 1;

2) разрушение в результате напряжений: точки с координатами главных напряжений σ₁ и σ₂ должны располагаться ниже диаграммы предельных напряжений (ДПН) листового материала σ₁=f(σ₂) с определенным запасом P_s пластичности по напряжениям; ДПН строят с помощью ДПД по уравнениям связи между деформациями и напряжениями; ДПН соответствует предельному эллипсу пластичности σ 1 2 − σ 1 σ 2 + σ 2 2 = σ s 2 .

Напряжение текучести σ_s в зависимости от интенсивности деформаций ε_i=ln(l+δ_p) рассчитывают с учетом упрочнения заготовки по формуле (Жарков В.А. Моделирование в системе Marc обработки материалов в машиностроении. Часть 7. Испытание и правка растяжением. - Вестник машиностроения, 2013, №3, с. 43-48):

σ s = σ 0,2 + σ в ( 1 + δ p ) ε i n , n=ln{l-σ_т/[σ_в(1+δ_p)]}/ln[ln(1+δ_p)],

где предел текучести σ_0,2, предел прочности σ_в и относительное равномерное удлинение δ_р для начала образования шейки на образце определяют по ГОСТ 11701-84 “Металлы. Методы испытаний на растяжение тонких листов и лент”.

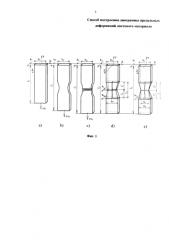
Базовую точку на ДПД определяют при испытании по ГОСТ 11701-84, при котором образец претерпевает три основные стадии растяжения: а - равномерное удлинение, когда на каждом этапе растяжения уменьшающиеся толщина и ширина образца одинаковы вдоль расчетной длины; b - неравномерное диффузное удлинение с образованием все увеличивающейся шейки за счет уменьшения толщины и ширины образца в зоне шейки; c - локальное утонение в виде локального уменьшения толщины, ширины и площади поперечного сечения шейки и разрыв образца в этом месте шейки. На фиг. 1 показана расчетная длина образца в конце каждой из этих трех стадий: a - конец равномерного удлинения; b - конец образования шейки; c - конец разрыва; d - расчетная схема шейки после разрыва в виде двух многогранников-обелисков; e - расчетная схема шейки после разрыва в виде двух многогранников-клиньев.

Расчет равномерного уменьшения ширины образца на первой стадии растяжения образца выполняют по следующей схеме. Металлургические комбинаты поставляют на машиностроительные предприятия лист, как правило, только с одной характеристикой пластичности листового материала - относительное удлинение после разрыва δ_f по ГОСТ 11701-84, и только по дополнительным техническим условиям в сертификате на лист приводят относительное равномерное удлинение δ_р, иначе δ_l,p в направлении длины l образца, и коэффициент анизотропии R_а по ГОСТ 11701-84. Если в сертификате на выбранный лист известно только δ_f и не известно δ_p, а машина для испытания на растяжение образца из листового материала с целью определения δ_p отсутствует, то сначала для аналогичного по механическим свойствам листового материала с известными значениями δ_p и δ_f рассчитывают коэффициент C=δ_f/δ_p, а затем для выбранного листового материала рассчитывают δ_p=δ_f/C. На основании этих двух свойств δ_l,p и R_а и выполняют расчет равномерного уменьшения ширины b образца ε_b,p, которое требуется для построения ДПД. При испытании на растяжение образца с исходными размерами s₀, b₀, l₀ (s₀ - толщина, b₀ - ширина, l₀ - начальная расчетная длина) в момент окончания равномерного удлинения и начала образования шейки (когда сила растяжения максимальна) размеры образца равны s_p, b_p, l_p и δ_l,p=(l_p-l₀)/l₀, ε_l,p=ln(l_p/l₀)=ln(1+δ_l,p). В этот момент коэффициент анизотропии равен R_a=ln(b_p/b₀)/ln(s_p/s₀)=ln(b_p/b₀)/ln[l₀b₀/(l_pb_p)], откуда находим логарифмическую деформацию ε_b,p=ln(b_p/b₀)=-R_a/(1+R_a)ln(1+δ_l,p) и из уравнений ε_b,p=ln(1+δ_b,p), δ_b,p=(b_p-b₀)/b₀ - относительную деформацию δ_b,p=ехр(ε_b,p)-1 по ширине. Из условия несжимаемости листового материала ε_l,p+ε_b,p+ε_s,p=0, которое строго справедливо только для логарифмических деформаций ε и справедливо лишь приближенно для относительных деформаций δ, определяют равномерное уменьшение толщины образца: ε_s,p=-ε_l,p-ε_b,p, δ_s,p=(s_p-s₀)/s₀=exp(ε_s,p)-1.

На производстве для повышения точности и качества, а также для оценки штампуемости детали на заготовку наносят делительную сетку, после штамповки в опасных местах детали по сеткам рассчитывают деформации, сравнивают их с ДПД, определяя запас пластичности до разрушения, и, в случае необходимости, назначают меры для уменьшения деформаций в опасных местах. Часто расчет деформаций заготовки по сеткам заменяют или совмещают с CAD/CAE-моделированием, при котором также необходима ДПД.

ДПД листового материала в виде функциональной зависимости ε₁=f(ε₂) строят по точкам, полученным по результатам испытаний на одноосное и двухосное растяжение различных по форме и размерам вырезанных из этого листового материала образцов, дающих различные точки на ДПД. На образец толщиной s₀ наносят ячейки делительной сетки, обычно в виде окружностей диаметром l₀. Диаметр ячеек подбирают таким образом, чтобы после испытания вблизи места разрыва образца окружности превращались в овалы или эллипсы с малой осью симметрии длиной l_min и большой осью симметрии длиной l_max, а толщина s_f образца плавно увеличивалась в направлении от места разрыва к захвату испытательной машины. При этом сдвиговые деформации и касательные напряжения в направлении малой и большой осей овала равны нулю, вследствие чего линейные деформации ε₁ и ε₂ и напряжения σ₁ и σ₂ соответственно в направлении большой и малой осей овала являются главными. Третье главное напряжение σ₃ в направлении толщины листового материала равно нулю. Оси овалов l_min и l_max измеряют и рассчитывают ε₁=ln(l_max/l₀) и ε₂=ln(l_min/l₀) в центре ячейки. Третью главную деформацию ε₃=ln(s_f/s₀) рассчитывают или по результатам измерений толщины s_f в центре ячейки, или из условия ε₁+ε₂+ε₃=0 несжимаемости листового материала: ε₃=-ε₁-ε₂. Если измеряют все три деформации ε₁, ε₂ и ε₃, то условие несжимаемости используют для оценки точности измерений.

Для построения ДПД на сетке прямоугольной системы координат откладывают: в положительном и отрицательном направлениях горизонтальной оси абсцисс - наименьшую деформацию ε₂=ln(l_min/l₀); в положительном направлении вертикальной оси ординат - наибольшую деформацию ε₁=ln(l_max/l₀), причем из условия ε₁+ε₂+ε₃=0 несжимаемости листового материала следует, что из трех деформаций ε₁, ε₂ и ε₃, как минимум, одна деформация во время пластического деформирования листового материала имеет положительное значение. Так как разрушение образца в процессе испытания или заготовки из листового материала в процессе штамповки детали может происходить только вследствие утонения, то всегда s_f<s₀, и деформации δ_s,f=(s_f-s₀)/s₀, ε₃=ln(s_f/s₀)=ln(1+δ_s,f) ячейки вблизи места разрыва образца или заготовки всегда будут иметь отрицательные значения.

Левая половина ДПД при ε₂<0 соответствует одноосному растяжению со сжатием элементов листового материала, ось ε₂=0 - плоской деформации, правая половина ДПД при ε₂>0 - двухосному растяжению элементов листового материала.

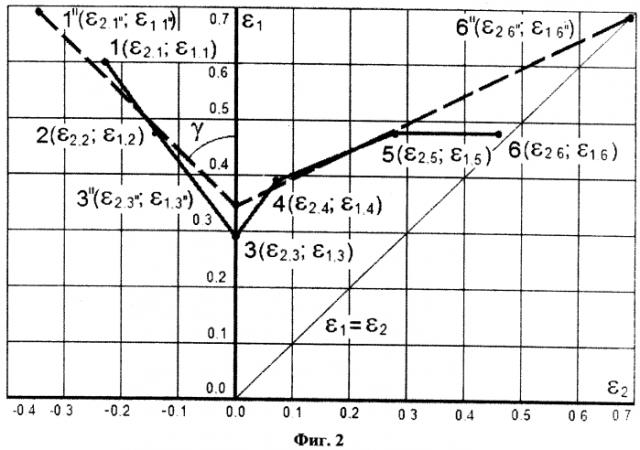
Вводят обозначения для базовой точки 1(ε_2,1; ε_1,1), вторая цифра в индексах означает номер точки на ДПД. Обозначения остальных точек ДПД аналогичны, изменяется только вторая цифра в индексах.

В качестве примера на фиг. 2 в верхней полуплоскости (ε₂, ε₁) сплошной линией показана экспериментально построенная ДПД ε₁=f(ε₂) в логарифмических деформациях (ε₂, ε₁) для широко применяемой в промышленности листовой стали: оцинкованная низкоуглеродистая сталь марки 01ЮТ ВОСВ ГЦ по ТУ 14-105-685-2002 с номинальной толщиной s₀=0,7 мм, где категория ВОСВ - весьма особо сложная вытяжка, ГЦ - горячеоцинкованный прокат. В расчетах технологии изготовления деталей из листового материала необходимо использовать свойства образцов, вырезанных под тем углом θ_r по отношению к направлению прокатки листового материала, где худшие характеристики пластичности, чтобы был дополнительный запас пластичности при штамповке деталей из листового материала на производстве. Для листового проката из стали θ_r=90°. После проведения испытаний по ГОСТ 11701-84 получены и рассчитаны по выведенным выше формулам механические свойства образца шириной b₀=12,5 мм из этой стали: предел текучести σ_0,2=171 Н/мм², предел прочности σ_в=304 Н/мм², относительное и логарифмическое равномерные удлинения δ_p=δ_l,p=0,24, ε_l,p=0,215; относительное удлинение после разрыва δ_f=δ₈₀=0,408 для образцов с начальной расчетной длиной 80 мм, коэффициент анизотропии R_a=2,722; относительное и логарифмическое равномерные уменьшения ширины образца δ_b=δ_b,p=-0,145, ε_b,p=-0,157; относительное и логарифмическое равномерные уменьшения толщины образца δ_s,p=-0,0563, ε_s,p=-0,058.

Если точку с координатами для конца равномерного удлинения и начала образования шейки на образце нанести на экспериментально построенную ДПД ε₁=f(ε₂), то эта точка будет находиться значительно ниже ДПД. Такое большое отличие объясняется тем, что ДПД строят по изменению нанесенной на образец делительной сетки вблизи места разрыва шейки образца (фиг. 1, с), а не в момент начала образования шейки (фиг. 1, а). Для листов с высокими характеристиками пластических свойств начало образования шейки еще не считается началом разрыва образца на испытательной машине или заготовки при штамповке детали на производстве. Однако ГОСТ 11701-84 не предусматривает расчет ε₂ и ε₁ вблизи места разрыва, хотя точка с этими координатами является базовой, с которой должно начинаться построение ДПД. Этот пробел и восполняют в данном способе.

Координаты базовой точки 1″(ε_2,1″; ε_1,1″) на ДПД определяют по механическим свойствам из сертификата на листовой материал по ГОСТ 11701-84 по следующей схеме.

Нижнюю и верхнюю части шейки после разрыва образца аппроксимируют расчетной схемой в виде двух одинаковых многогранников типа обелиска высотой l n ' = l n / 2 , имеющих расположенные в параллельных плоскостях большие и малые основания-прямоугольники и соединенных по малым основаниям; противоположные грани одинаково наклонены к каждому основанию (фиг. 1, d). При испытании образца по ГОСТ 11701-84 начальная расчетная длина l₀ в конце равномерного удлинения и начала образования шейки увеличивается до значения l_p=(1+δ_p)l₀=(1+0,24)80=99,2 мм, а после диффузного образования шейки, локального утонения и разрыва образца дополнительно увеличивается до значения l_f=(1+δ_f)l₀=(1+0,408)80=112,64 мм при дополнительном ходе захвата испытательной машины h_n=(l_f-l_p)=112,64-99,2=13,44 мм. Так как в образовании шейки участвуют сопряженные с верхней и нижней частями шейки участки образца, то длина шейки l_n≥h_n. На верхнем и нижнем концах шейки большие основания двух многогранников имеют размеры, соответствующие концу равномерного удлинения образца: ширина b_p=(1+δ_b,p)b₀=(1-0,145)·12,5=10,687 мм, толщина s_p=(1+δ_s,p)s₀=(1-0,0563)·0,7=0,661. При ходе h_n объем V этого основания равен: V=s_pb_ph_n. Экспериментально установлено, что объем V₂ образца, идущий на образование шейки, равен (40…50)%, в среднем, 45% от V: V₂=0,45s_pb_ph_n=0,45·0,661·10,687·13,44=42,724 мм³. Объем V₁ образца, идущий на образование одной нижней или верхней половины шейки: V₁=V₂/2=21,362 мм³. При малой номинальной толщине s₀ образца, как в данном примере, толщина s_c шейки в месте разрыва s_c≈0, и два многогранника-обелиска шейки превращаются в два многогранника-клина (фиг. 1, e), каждый из которых имеет объем V₁ и высоту l n ′ ≈ h n / 2 = 13,44 / 2 = 6,72 мм. Теперь можно определить ширину b_c шейки в месте разрыва: b c = ( 6 V 1 / l n ′ − 2 s p b p ) / s p = 7,481 мм.

Верхний и нижний многогранники делим пополам по длинам l n ′ и l n ″ поперечными сечениями, перпендикулярными оси Y, и принимаем, что на длине l n / 2 = l n ′ / 2 + l n ″ / 2 соединенных в одном общем малом основании половин многогранников происходило локальное утонение и разрушение образца, где ячейки делительной сетки на передних гранях многогранников также были разрушены, а на прилегающей к большому основанию передней грани каждой из половин многогранников ячейки делительной сетки не были разрушены, превратились в овалы, большие оси которых равны половине передней грани, были измерены и рассчитаны деформации вблизи места разрыва. Так как толщина образца по длине l n ′ каждого многогранника распределена по линейному закону от s_p до s_c≈0 и так как деформации рассчитывают в центре ячейки посередине большой оси овала, расположенной вдоль образца, то для определения толщины s_f образца в центре овальной ячейки следует в сечении образца плоскостью YZ длину по грани каждого многогранника и соответственно (из принципа подобия) длину l n ′ по оси Y и толщину s_p основания многогранника разделить на 4 части и умножить на 3: s_f=3/4·s_p=3/4·0,661=0,495 мм.

В итоге абсциссу ε_2,1″ базовой точки 1″(ε_2,1″; ε_1,1″) на ДПД рассчитывают для линейного растяжения образца при условии ε_2,1″=ε_1,1″=-2ε_2,1″: ε_2,1″=ε_3,1″=ln(s_f/s₀)=ln(0,495/0,7)=-0,3465, а ордината равна ε_1,1″=-2ε_2,1″=-2(-0,3465)=0,693.

На экспериментально построенной ДПД (фиг. 2) в виде сплошной линии логарифмических деформаций ε₁=f(ε₂) из полученной точки 1″(ε_2,1″; ε_1,1″) проводят пунктирную прямую до пересечения с осью ε₁ в точке 3″(ε_2,3″; ε_1,3″) с абсциссой ε_2,3″=0. Эту пунктирную прямую проводят под углом γ к оси ординат, который для широко применяемых в автомобильной и других отраслях промышленности листовых материалов равен 45°. Получают ординату ε_1,3″ точки 3″(ε_2,3″; ε_1,3″):ε_1,3″=ε_1,1″+ε_2,1″ и уравнение ε₁=f(ε₂) левой прямой 1″-3″ ДПД:

ε₁=-ε₂+ε_1,3″ при ε_2,1″≤ε₂≤0.

Для стали 01ЮТ ВОСВ ГЦ ε_1,3″=0,3465.

Если требуется, то отрезок прямой 1″-3″ ДПД продлевают влево до точки с координатами ε_2,min, ε 1 ′ , max . Например, из точки 1″(ε_2,1″; ε_1,1″) до новой точки 0″(ε_2,0″; ε_1,1″) при ε_2,0″=ε_2,min, ε 1, 0 ″ = ε 1 ′ , max проводят отрезок прямой с уравнением ε₁=-ε₂+ε_1,3″ при ε_2,min≤ε₂≤ε_2,1″.

Для построения правой половины ДПД по двум точкам 3″ и 6″ координаты первой точки 3″(ε_2,3″; ε_1,3″) на оси ε₁ уже известны, а координаты второй точки 6″(ε_2,6″; ε_1,6″) определяют по следующей схеме. Для точки 1″(ε_2,1″; ε_1,1″) с абсциссой ε_2,1″=-0,3465 и ординатой ε_1,1″=0,693 при одноосном растяжении образца интенсивность деформаций равна ε i ′ = 0,693 .

При испытании на двухосное растяжение образцов полусферическим пуансоном с применением смазочных материалов в сочетании с антифрикционными пленками, например из тефлона, для уменьшения трения между образцом и пуансоном или при испытании на двухосное растяжение образцов жидкостью деформации ε₁ и ε₂ вдоль двух взаимно перпендикулярных касательных к поверхности отформованного пуансоном или жидкостью полюса образца равны между собой: ε₁=ε₂=-0,5ε₃, и формула для интенсивности деформаций ε_i принимает вид: ε i ″ = | ε 3 | = | ln ( s / s 0 ) | или ε i ″ = ln ( s 0 / s ) .

Экспериментально установлено, что при испытании на двухосное растяжение образца полусферическим пуансоном или жидкостью интенсивность деформаций ε i ″ элементов вблизи места разрыва образца в 2 раза больше интенсивности деформаций ε i ′ элементов образца вблизи места разрыва при испытании на одноосное растяжение: ε i ″ = 2 ε i ′ , в данном примере, ε i ″ = 2 ⋅ 0,693 = 1,386 .

Из условия ε 1 = ε 2 = 0,5 ε i ″ = 0,693 для двухосного растяжения строят точку 6″ (ε_2,6″; ε_1,6″) выше оси абсцисс ε₂ с абсциссой ε_2,6″=0,693 и ординатой ε_1,6″=0,693, проводят пунктирную линию (фиг. 2) с уравнением ε₁=f(ε₂) правой половины ДПД в виде прямой через две известные точки 3″(ε_2,3″; ε_1,3″) и 6″(ε_2,6″; ε_1,6″):

(ε₁-ε_1,3″)/(ε_1,6″-ε_1,3″)=(ε₂-ε_2,3″)/(ε_2,6″-ε_2,3″) при 0≤ε₂<ε_2,6″.

Если требуется продлить правую половину ДПД вправо до точки с координатами ε_2,max, ε 1 ″ , max , то из условия, что ε₁ является наибольшей деформацией и что всегда ε₁≥ε₂, следует, что продленная часть ДПД должна быть выше, касаться или совпадать с прямой ε₁=ε₂. Например, из точки 6″(ε_2,6″; ε_1,6″) до новой точки 7″(ε_2,7″; ε_1,7″). При ε_2,7″=ε_2,max, ε 1, 7 ″ = ε 1 ″ , max проводят отрезок прямой с уравнением ε₁=f(ε₂): ε₁=ε₂ при ε_2,6″≤ε₂≤ε_2,max.

На фиг. 2 видно, что построенная по данному способу ДПД (пунктирная линия) вблизи оси ε₁, где располагаются точки с координатами опасных мест на заготовке из данного листового материала при вытяжке сложных деталей типа кузовных, достаточно точно соответствует экспериментальной ДПД (сплошная линия).

Построенную по данному способу ДПД используют на производстве для определения опасности разрушения заготовки в процессе штамповки детали или вводят в CAD/CAE-систему, например в систему Marc корпорации MSC Software (США), которая объединяет в себе CAD-программу и CAE-программу, или в программу AutoForm фирмы AutoForm Engineering (Швейцария), в виде приведенных выше уравнений или в виде большого количества координат точек, полученных по этим уравнениям. По этим данным CAD/CAE-система строит ДПД в прямоугольной системе координат с заданным масштабом координатной сетки и после компьютерного моделирования процесса штамповки на эту координатную сетку выводит массив точек с координатами ε₁ и ε₂ всех элементов заготовки из данного листового материала на всех этапах штамповки заготовки. По номеру и цвету точек определяют те элементы на штампуемой заготовке, которые близко расположены (с учетом запаса пластичности) или вышли за ДПД и где велика вероятность разрушения заготовки, и разрабатывают мероприятия по уменьшению вероятности разрушения заготовки в процессе обработки на производстве.

Построенная по данному способу диаграмма предельных деформаций изотропного (ДПДИ) листового материала является первым приближением. Со временем, по мере проведения дополнительных испытаний, на ДПДИ накладывают диаграмму предельных деформаций анизотропного (ДПДА) листового материала как последующие приближения для реального на производстве анизотропного материала, ДПДА вводят в CAD/CAE-систему и более точно, чем с ДПДИ, моделируют и проектируют процесс листовой штамповки, а также при помощи коэффициента анизотропии A_θ=(ε₃-ε₂)/(0,5ε₁), ε₁=ln(1+δ_p), ε₂=ln(1+δ_b), ε₃=-ε₁-ε₂ (Жарков В.А. Моделирование в системе Marc обработки материалов в машиностроении. Часть 6. Вытяжка детали сложной формы. - Вестник машиностроения, 2012, №9, с. 67-73) для углов θ вырезки образцов по отношению к направлению прокатки листового материала получают качественную и количественную характеристику влияния анизотропии на предельное формоизменение листового материла.

Технический результат заключается в том, что, не дожидаясь проведения сложных и дорогостоящих испытаний листового материала на испытательной машине и в штампе-приборе, можно по данному способу быстро построить ДПД на основе только двух приводимых в сертификате на листовой материал стандартных механических свойств по ГОСТ 11701-84: относительного равномерного удлинения и коэффициента анизотропии, и использовать эту ДПД как в CAD/CAE-системе, так и на производстве для расчета вероятности разрушения листовой заготовки на операциях листовой штамповки. Данный способ сокращает время и повышает качество проектирования технологических процессов и оснастки, дает экономию листового материала за счет сокращения процента брака при отладке технологических процессов, а также значительно упрощает выбор листового материала и оборудования для листовой штамповки деталей, например кузовных деталей легковых автомобилей и другой техники.

Способ построения диаграммы предельных деформаций листового материала, заключающийся в том, что на полученный из листового материала образец наносят делительную сетку, образец испытывают, измеряют делительную сетку, рассчитывают наименьшую главную деформацию ε₂ и наибольшую главную деформацию ε₁ и по нанесенным на координатную сетку значениям деформаций ε₂ по оси абсцисс и ε₁ по оси ординат строят диаграмму предельных деформаций ε₁=f(ε₂), отличающийся тем, что диаграмму предельных деформаций строят по относительному равномерному удлинению и коэффициенту анизотропии, приводимых в сертификате на листовой материал, по которым, соответственно, вычисляют отрицательную абсциссу и положительную ординату первой точки на левой половине диаграммы предельных деформаций, из построенной первой точки проводят прямую под углом 45° к осям координат до пересечения с осью ординат во второй точке и получают левую половину диаграммы предельных деформаций, третью точку на правой половине диаграммы предельных деформаций строят с абсциссой и ординатой из условия, что при испытании на двухосное растяжение образца полусферическим пуансоном или жидкостью интенсивность деформаций элементов вблизи места разрыва образца в 2 раза больше интенсивности деформаций элементов образца вблизи места разрыва при испытании на одноосное растяжение, известной для левой половины диаграммы предельных деформаций, соединяют вторую и третью точки прямой и получают правую половину диаграммы предельных деформаций.