Способ уравнивания геодезических сетей из четырехугольников
Иллюстрации
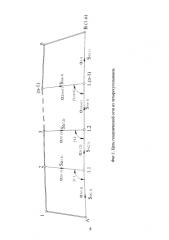
Показать всеИзобретение относится к геодезии, в частности к способам уравнивания геодезических сетей. Способ уравнивания геодезических сетей из четырехугольников включает определение дирекционных углов сторон сети, вычисление предварительных координат точек сети последовательными угловыми засечками по формулам Гаусса, составление условного уравнения дирекционных углов, в результате решения которого определяются поправки в дирекционные углы сторон сети и затем координаты искомых точек. В имеющейся цепи, в которой пункты А, 1, 2, …, n, В - исходные, координаты которых определены с достаточно высокой точностью. Внутри сети выполнены угловые измерения, позволяющие найти дирекционные углы сторон сети в каждом четырехугольнике. При использовании гиротеодолитов эти дирекционные углы можно сразу измерить. Тогда последовательными угловыми засечками по формуле Гаусса можно вычислить предварительные координаты точек 1.1, 1.2, …, 1.(n-1). Техническим результатом изобретения является более точный способ уравнивания геодезических сетей путем введения поправок в дирекционные углы в соответствии с составленным условным уравнением дирекционных углов. 1 ил.
Реферат
Изобретение относится к области геодезии, в частности, к способам уравнивания геодезических сетей.
Известен способ посредственных линейных измерений при разбивке строительной сетки, где полигон разбивают на четырехугольники и измеряют по периметру все стороны и все углы четырехугольников внутри полигона. Другие стороны вычисляют по формулам (Субботин И.Е., Мазницкий А.С. Справочник строителя по инженерной геодезии. Киев, 1972 г - С. 179).
Также известен метод построения планового геодезического обоснования в виде сети из четырехугольников без диагоналей, где в каждом из них измеряются четыре угла и одна сторона, а в первом и последнем четырехугольниках - четыре угла и две стороны. (Ливанов М.М. Инженерно-геодезическая съемка и составление исполнительных планов промышленных предприятий - М.: 1966. - С. 47).
Недостатком известных технических решений является уравнивание таких сетей упрощенным способом, а именно: распределение возникающих невязок в приращениях координат fx и fy поправок на все приращения (или пропорционально длинам сторон ходовой линии).
Техническим результатом является разработка более строгого способа уравнивания таких сетей путем составления и решения условного уравнения дирекционных углов, введения поправок в измеренные дирекционные углы и вычисления окончательных координат искомых точек сети.
Технический результат достигается тем, что в способе уравнивания геодезических сетей из четырехугольников, включающем определение дирекционных углов сторон сети (путем измерения горизонтальных углов или с использованием гиротеодолитов), вычисление предварительных координат точек сети последовательными угловыми засечками по формулам Гаусса, составление условного уравнения дирекционных углов, в результате решения которого определяются поправки в дирекционные углы сторон сети и затем координаты искомых точек.
Новизна заявленного способа обусловлена тем, что уравнивание таких сетей выполняется не упрощенным, а более строгим способом путем введением поправок в дирекционные углы в соответствии с составленным условным уравнением дирекционных углов и вычисление окончательных координат точек сети.
Суть изобретения заключается в следующем. Пусть имеем цепь (Фиг. 1), в которой пункты А, 1, 2, …, n, В - исходные, координаты которых определены с достаточно высокой точностью. Внутри сети выполнены угловые измерения, позволяющие найти дирекционные углы сторон сети в каждом четырехугольнике. При использовании гиротеодолитов эти дирекционные углы можно сразу измерить. Тогда последовательными угловыми засечками по формуле Гаусса можно вычислить предварительные координаты точек 1.1, 1.2, …, 1.(n-1)
Для стороны S1.n путем решения обратной геодезической задачи вычисляют ее дирекционный угол по формуле:
где X1.n, Y1.n - известные координаты точки B1.n;
X1(n-1), Y1(n.1) - координаты точки 1(n-1), вычисленные последовательными угловыми засечками.
В результате для дирекционного угла этой линии появится угловая невязка:
где α1.n(изм) - измеренное значение дирекционного угла;
α1.n(выч) - вычисленное значение дирекционного угла по формуле 1.
Тогда условное уравнение дирекционных углов будет:
Для получения коэффициентов при неизвестных поправках в дирекционные углы потребуется частные производные по каждой измеренной величине.
Согласно формулам Гаусса для точки 1.1 запишем:
Дифференцируя (4) по каждому измеренному дирекционному углу, после преобразований получим:
где γ1.1 - горизонтальный угол определяемый как разность дирекционных углов линий α2(1.1) и α1(1.2).
На положение точки 1.2 будут влиять ошибки дирекционных углов α1(1.1), α2(1.1) и ошибки дирекционных углов α1(1.2), α2(1.2).
Для точки 1.2 запишем:
Дифференцируя (6), найдем частные производные по всем четырем дирекционным углам, получим:
Следуя подобным образом, получим следующий алгоритм вычисления коэффициентов при поправках в дирекционные углы.
где j - номер четырехугольника;
XОП.j, YОП.j, - координаты определяемой точки в j-том четырехугольнике;
XЛ.j, YЛ.j, - координаты левой точки диагонали (по отношению к определяемой точки) в j-том четырехугольнике;
α1.i, и α2.i - дирекционные углы i-того четырехугольника, влияющие на определение координат в j-том четырехугольнике.
Дифференцируя уравнение (3), получим условное уравнение дирекционных улов для рассматриваемой сети следующего вида:
Решая полученное уравнение (9) по способу наименьших квадратов под условием [V2] = min, т.е. считая, что все измеренные дирекционные углы равноточны, получим искомые поправки к дирекционным углам, вводя которые в результате измерений дирекционных углов получим последовательными угловыми засечками координат определяемых пунктов.
Способ уравнивания геодезических сетей из четырехугольников, включающий измерения углов в четырехугольниках и длины одной стороны, а в первом и последнем четырехугольнике длины двух сторон, в результате чего вычисляют длины остальных сторон, полученные невязки распределяются поровну по ходовой линии, отличающийся тем, что поправки вводят в дирекционные углы, при этом их величину получают путем решения условного уравнения дирекционных углов, коэффициенты которого при искомых поправках в дирекционные углы вычисляют по алгоритму: где j - номер четырехугольника;XОП.j, YОП.j, - координаты определяемой точки в j-том четырехугольнике;XЛ.j, YЛ.j, - координаты левой точки диагонали (по отношению к определяемой точки) в j-том четырехугольнике;α1.i, и α2.i - дирекционные углы i-того четырехугольника, влияющие на определение координат в j-том четырехугольнике;S - длина стороны четырехугольника,а искомые поправки в дирекционные углы находят путем решения условного уравнения дирекционных углов по способу наименьших квадратов при условии [V2] = min, принимая все измеренные дирекционные углы равноточными, где ƒα1.n - угловая невязка в дирекционный угол,после чего полученные поправки к дирекционным углам вводят в результаты измерения дирекционных углов, а координаты определяемых пунктов вычисляют последовательными угловыми засечками.