Способ адаптивного обнаружения сигналов движущихся целей на фоне многокомпонентных пассивных помех

Способ адаптивного обнаружения сигналов движущихся целей на фоне многокомпонентных пассивных помех

Иллюстрации

Показать все

Реферат

Предлагаемый способ относится к радиотехнике, в частности к цифровой обработке радиолокационных сигналов. В практике защиты РЛС от сигналов многокомпонентных пассивных помех, вызванных совокупностью отражений от местных предметов, облаков, гидрометеоров, дипольных помех, применяют различные способы обнаружения полезных целей.

Известен способ обнаружения сигналов на фоне пассивных помех, основанный на предварительной адаптивной фильтрации пассивной помехи с помощью соответствующего выбора весовых коэффициентов фильтра [1] и последующим сравнением огибающей выходного сигнала с порогом. Основным недостатком данного способа является его низкая эффективность, обусловленная использованием фиксированных весовых коэффициентов для фильтрации сигналов, имеющих доплеровское смещение спектра. Кроме того, отсутствие нормирования сигнала до сравнения с порогом приводит к отсутствию стабилизации ложных тревог.

Известен способ обнаружения сигналов на фоне пассивных помех [2], который включает в себя многоканальное весовое когерентное накопление, выделение огибающих после многоканального весового когерентного накопления, адаптивную нормировку огибающих сигналов в каждом из каналов и их объединение, формируя тем самым выходной сигнал, сравниваемый с порогом обнаружения.

Недостатком данного способа является пониженная эффективность защиты от пассивных помех по сравнению с оптимальной обработкой за счет того, что формирование вида частотных характеристик при весовом когерентном накоплении осуществляется без учета таких параметров, как ширина спектра флюктуаций пассивной помехи и доплеровского смещения ее частоты. Использование во всех каналах одинаковой весовой функции для уменьшения уровня боковых лепестков частотных характеристик каналов обеспечивает симметричное и равномерное подавление всех боковых лепестков фильтров, в то время как при оптимальной обработке осуществляется максимизация отношения сигнал/помеха за счет разной коррекции частотных характеристик фильтров только в зоне нахождения спектра флюктуации сигналов пассивной помехи.

Наиболее близким по технической сущности к предлагаемому способу является патент США [3], в котором обработка строится следующим образом. На входе отраженные сигналы, представленные своими цифровыми квадратурными составляющими, подвергаются многоканальной доплеровской фильтрации и многоканальному когерентному накоплению в процессоре ДПФ, на выходе которого вычисляются огибающие, которые нормируются, объединяются и подаются на порог обнаружения, причем вычисление весовых коэффициентов для многоканальной доплеровской фильтрации осуществляется предварительно по приближенной формуле для выбранной заранее формы спектра флюктуаций пассивной помехи. В данном способе коррекция частотных характеристик при многоканальной доплеровской фильтрации производится более оптимально с учетом близкой к реальности пассивной помехи, имеющей, например, гауссов спектр. Для чего предварительно весовые коэффициенты, обеспечивающие оптимизацию частотных характеристик, рассчитываются по формуле (см. описание патента)

,

где W - вектор весовых коэффициентов для многоканальной доплеровской фильтрации,

R^-1 - обратная корреляционная матрица для предварительно заданной модели пассивной помехи и хранящаяся в постоянном запоминающем устройстве,

S - вектор полезного сигнала, который для цели с неизвестной скоростью формируется в виде коэффициента Фурье

S=(1,e^j2πn/N, e^j4πn/N, …, e^j2π(N-1)/N),

где n - номер доплеровского канала, N - число импульсов в пачке.

В способе, взятом в качестве прототипа, вычисление весовых коэффициентов в силу невозможности в реальном масштабе времени оценить многомерную комплексную корреляционную матрицу и сделать ее обращение использован упрощенный подход, основанный на рассмотрении модели пассивной помехи, например, с гауссовой формой спектра и расчета весовых коэффициентов без оценки и обращения всей корреляционной матрицы в реальном масштабе времени. Вместо этого производится оценка в реальном масштабе времени только модуля межпериодного коэффициента корреляции и его аргумента - межпериодного доплеровского набега фазы помехи. И на их основе выбираются из запоминающегося устройства заранее рассчитанные весовые коэффициенты для неподвижной пассивной помехи, которые корректируются с учетом оценки межпериодного доплеровского набега фазы. К сожалению, заранее все многообразие форм спектра предусмотреть невозможно, особенно, если пассивная помеха многокомпонентная, т.е. имеет многомодовый спектр отраженных сигналов одновременно от местных предметов, гидрометеоров и дипольных отражателей. Отсюда и низкая эффективность данного способа

Чтобы повысить эффективность защиты РЛС от пассивных помех с многомодовыми спектрами, предлагается рассчитывать весовые коэффициенты доплеровского фильтра по отраженным сигналам от многокомпонентной пассивной помехи, используя аппроксимацию реальной помехи процессом авторегрессии [4]. Это позволит также не производить оценку корреляционной матрицы и ее обращение, а в реальном масштабе времени оценивать коэффициенты авторегрессии. Воспользуемся в нашем случае иным представлением формулы (1), избежав оценивания и обращения комплексной корреляционной матрицы. Обратную корреляционную матрицу для процесса авторегрессии можно представить в виде разложения на диагональную D и верхнюю, и нижнюю треугольные матрицы коэффициентов авторегрессии A:

В соответствии с (2) получим:

где Z_вх, Z_вых комплексные сигналы, представляемые своими квадратурными составляющими на входе и выходе доплеровского фильтра, A - комплексный вектор коэффициентов авторегрессии. Левую часть формулы (3) в терминах патента прототипа можно рассматривать как многоканальную доплеровскую фильтрацию, а правую как когерентное многоканальное накопление в процессоре ДПФ. А диагональные члены D - это результат нормирования сигналов в каждом канале фильтра.

Преобразуем (3) так, что совместим доплеровскую фильтрацию с когерентным накоплением сигналов цели с неизвестной скоростью

где n - номер доплеровского канала, S(n) - коэффициенты Фурье

S(n)=(1,e^j2πn/N, e^j4πn/N, …, e^j2π(N-1)/N),

N - число импульсов в пачке.

Таким образом, в предлагаемом способе при неизвестной скорости цели адаптивная обработка реализуется с помощью многоканальной доплеровской фильтрации, для каждого канала в котором используются свои весовые коэффициенты, учитывающие как оценки коэффициентов авторегрессии, так и коэффициенты разложения по Фурье, позволяя в отличие от прототипа фильтровать сигналы пассивной помехи с многомодовыми спектрами.

Таким образом, в известный способ адаптивного обнаружения целей на фоне многокомпонентных пассивных помех, включающий в себя многоканальную доплеровскую фильтрацию, с многоканальным когерентным накоплением в виде дискретного преобразования Фурье, результат которого подвергается вычислению огибающих, которые нормируются и объединяются с выделением максимального значения, введены существенные отличия в том, что для операции многоканальной доплеровской фильтрации весовые коэффициенты вычисляются в реальном масштабе времени векторным перемножением оцененных коэффициентов авторегрессии, и коэффициентов преобразования Фурье.

Это является важнейшим преимуществом и отличительным признаком предлагаемого способа, поскольку в этом случае удается без предварительного оценивания корреляционной матрицы помехи и ее обращения, используя непосредственно выборку наблюдений, получать в реальном масштабе времени оценки коэффициентов авторегрессии с помощью эффективного в вычислительном отношении алгоритма. При этом с помощью ограниченного числа коэффициентов авторегрессии удается для широкого класса многокомпонентных пассивных помех, имеющих многомодовые спектры обеспечивать эффективное обнаружение целей. Наиболее предпочтительным из алгоритмов оценивания коэффициентов авторегрессии с точки зрения эффективности является алгоритм Берга [5].

Еще одна отличительная особенность предложенного способа состоит в обработке нескольких пачек импульсов на разных частотах повторения или на разных несущих частотах, что позволяет улучшить скоростную характеристику обнаружителя сигналов по цели в целом. Для этого при обработке каждой пачки из M сигнал после отбора по максимуму каждой обработанной пачки импульсов запоминается и по окончании последней обработанной пачки отбирается максимум от всех полученных максимумов. Он и сравнивается с порогом обнаружения.

MAX{MAX₁|Z_1BXW₁(n)|,MAX₂|Z_2BXW₂(n)|…MAX_M|Z_MBBW_M(n)|}≥U_ПОР

С целью исключения подавления полезного сигнала при фильтрации предлагается усреднять оценки коэффициентов авторегрессии по нескольким элементам дальности.

Выигрыш в эффективности предложенного способа по сравнению с прототипом оценивался в пороговом сигнале для вероятности правильного обнаружения 0,5 и вероятности ложной тревоги 10^-1-10^-2. Расчет производился методом статистического моделирования в МАТЛАБ. Пассивная помеха задавалась протяженной по дальности, двухкомпонентной (с двухмодовым спектром) первая мода имела относительную ширину спектра флюктуаций по уровню -20 дБ Δ F 1 F П = 0,15 , вторая мода Δ F 2 F П = 0,25 . Каждая мода имела превышение над шумом 20 дБ с относительным доплеровским смещением F Д 1 F П = 0,35 и F Д 2 F П = 0,5 . Скорость цели задавалась 500 м/с. Число обрабатываемых импульсов 12 (две пачки по 6 импульсов на двух частотах повторения 400 Гц и 440 Гц.) Порядок авторегрессии был задан 5. Оценка коэффициентов авторегрессии производилась по программе из МАТЛАБ [6] для первой SF11 и второй SF22 пачек:

Формирование весовых коэффициентов производилось векторным перемножением оценок коэффициентов авторегрессии на коэффициенты Фурье

На Фиг. 1 показана частотная характеристика одного из каналов доплеровского фильтра, использующего оценки коэффициентов авторегрессии. Для способа, взятого прототипом, оценка модуля межпериодного коэффициента корреляции и межпериодного доплеровского набега фазы производилась по программе MATLAB

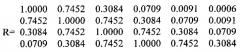
Данные оценки в предположении о гауссовой форме спектра помехи использованы для воспроизведения по оценкам модуля межпериодного коэффициента корреляции корреляционных матриц помехи без доплеровского смещения для первой и второй пачек, которые затем обращаются с помощью программы inv MATLAB. Ниже приведена в качестве примера восстановленная для первой пачки корреляционная матрица по оценке модуля межпериодного коэффициента корреляции, равного 0,7452:

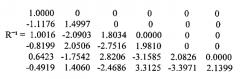
И соответствующая обратная матрица

После поворота вектора входной выборки наблюдений на угол в соответствии с полученной оценкой аргумента межпериодного коэффициента корреляции производится многоканальная доплеровская фильтрация с весами, где используются воспроизведенные обратные матрицы RE1 для первой пачки и RE2 для второй пачки:

Поскольку в описании способа прототипа рассматривается обработка только одной пачки, поэтому вначале сравнение предложенного способа с прототипом производилось при обработке одной пачки, т.е. когда выделенные огибающие на выходе доплеровских каналов после усреднения объединялись с отбором максимального значения с помощью функции max MATLAB, которое подавалось на порог обнаружения

Затем такое же сравнение двух способов было сделано при обработке двух пачек с разными двумя частотами повторения с отбором в соответствии с формулой предложенного способа максимума от двух максимумов при обработке каждой пачки.

Расчеты показали, что выигрыш в пороговом сигнале предложенного способа по сравнению со способом, взятым в качестве прототипа как при обработке одной пачки, так и для двух пачек, составляет 5-10 дБ. Пояснить полученную более высокую эффективность обнаружения достаточно просто, если сравнить корреляционные функции каждой из двух компонент пассивной помехи с корреляционной функцией, полученной по оценке результирующего модуля межпериодного коэффициента корреляции двухкомпонентной пассивной помехи (см. Фиг. 2). Кроме того, также ошибочно формируется и оценка межпериодного допплеровского набега фазы (аргумента межпериодного коэффициента корреляции) по двум смещенным по доплеру компонентам помехи. Отсюда «оптимальные» весовые коэффициенты в прототипе не соответствуют реальной помеховой обстановке, которую заранее не удается предусмотреть, даже сохранив в запоминающем устройстве огромное множество готовых весовых коэффициентов, что и приводит к снижению у прототипа эффективности обнаружения полезных целей на фоне многокомпонентных пассивных помех.

Источники информации

1. Бакулев П.А., Степин В.М. Методы и устройства селекции движущихся целей. - М., "Радио и связь", 1986.

2. Патент США №3831174 G01s 9/06, 1974.

3. Патент США №4742353 G01s 13/6, 1988.

4. Marple S.L. "Digital Spectral Analysis", Englewood Cliffs, NJ: Prentice Hall, 1987, Chapter 7.

5. Бартенев В.Г., Кутепов В.Е. Сравнительный анализ двух способов формирования весовых коэффициентов в адаптивной системе селекции движущихся целей // Цифровая обработка сигналов. 2014. №2, С. 58-60.

6. Потемкин В.Г. "Справочник по MATLAB" Анализ и обработка данных. http://matlab.exponenta.ru/ml/book2/chapter8/.

1. Способ адаптивного обнаружения движущихся целей на фоне многокомпонентных пассивных помех, включающий в себя многоканальную доплеровскую фильтрацию с многоканальным когерентным накоплением в виде преобразования Фурье, результат которого подвергается вычислению огибающих, которые нормируются и объединяются с выделением максимального значения, отличающийся тем, что для операции многоканальной доплеровской фильтрации и многоканального когерентного накопления в виде преобразования Фурье весовые коэффициенты вычисляются в реальном масштабе времени векторным перемножением оценок коэффициентов авторегрессии и коэффициентов преобразования Фурье.

2. Способ адаптивного обнаружения движущихся целей на фоне многокомпонентных пассивных помех, включающий в себя многоканальную доплеровскую фильтрацию с многоканальным когерентным накоплением в виде преобразования Фурье, результат которого подвергается вычислению огибающих, которые нормируются и объединяются с выделением максимального значения, отличающийся тем, что с порогом обнаружения сравнивается на выходе в каждом элементе дальности максимум от нескольких максимумов огибающих сигналов, полученных при обработке каждой пачки эквидистантных импульсов с разными частотами повторения или несущими частотами, изменяемыми от пачки к пачке.

3. Способ по п. 1, отличающийся тем, что формирование оценок коэффициентов авторегрессии производят с усреднением этих оценок коэффициентов авторегрессии по нескольким элементам дальности.