Способ измерения курсовой скорости объекта

Способ измерения курсовой скорости объекта

Иллюстрации

Показать все

Реферат

Изобретение относится к радиотехнике и может быть использовано в системах ближней радиолокации для измерения курсовой скорости объекта по двум последовательно измеренным значениям его радиальной скорости.

Известен способ измерения радиальной скорости движущегося объекта, основанный на эффекте Доплера - трансформации частоты подвижным объектом (Теоретические основы радиолокации, под редакцией Ширмана Я.Д, М., Советское радио, 1970 г., стр. 51).

Измеряют трансформацию несущей частоты радиосигнала подвижным объектом по формуле: F_д=2f_ov_r/c=2v_r/λ_o,

где F_д - доплеровская поправка частоты (частота Доплера);

f_o - несущая частота измерителя скорости;

v_r - радиальная скорость движущегося объекта (в направлении на измеритель);

с - скорость света;

λ_о - рабочая длина волны измерителя скорости.

Из этого уравнения, решенного относительно радиальной скорости объекта, определяют ее по формуле:

Общим признаком аналога и изобретения является способ измерения радиальной скорости объекта.

Недостатком аналога является невозможность измерения курсовой скорости объекта при визировании объекта к его курсу под углами больше нуля и меньше 90°.

Известен «Способ измерения радиальной скорости объекта и устройство для его осуществления», принятое за прототип изобретения (Патент РФ №2535487, МПК G01S 13/58, 2013 г.). Устройство содержит: генератор одиночного прямоугольного импульса высокой частоты (ВЧ), передающую и приемную антенны, выключатель принимаемого радиосигнала, таймер и измеритель фазы. Выход генератора ВЧ соединен с входом передающей антенны и входом опорного радиосигнала измерителя фазы. Выход приемной антенны соединен с входом выключателя принимаемого радиосигнала, а его выход с сигнальным входом измерителя фазы. Выход таймера соединен с входом управляющего сигнала выключателя принимаемого радиосигнала.

Общим признаком прототипа и изобретения является способ измерения радиальной скорости объекта.

Недостатком прототипа является невозможность измерения курсовой скорости объекта при визировании объекта к его курсу под углами больше нуля.

Техническим результатом изобретения является устранение недостатков аналога - измерение курсовой скорости объекта при углах визирования к курсу больше нуля.

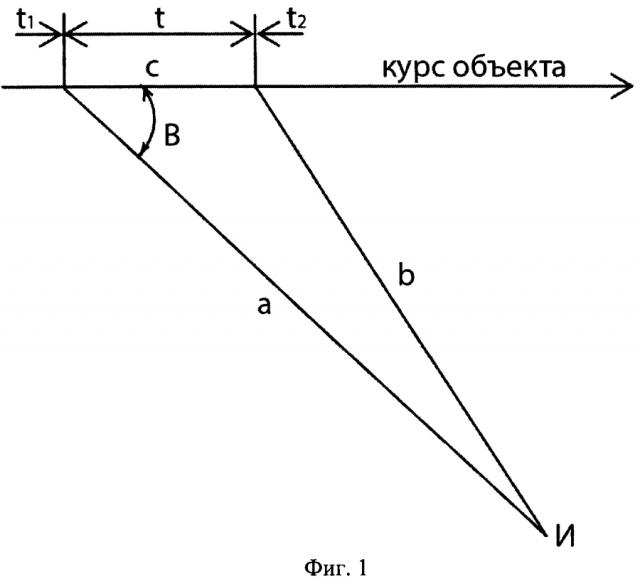
Изобретение поясняется фиг. 1, на которой представлена схема измерения курсовой скорости объекта и введены обозначения.

Горизонтальная линия со стрелкой обозначает направление движения объекта, курс;

И - точка пространства, вынесенная с курса объекта, где находится измеритель радиальной скорости;

t₁ - время первого измерения радиальной скорости объекта и расстояния от точки И до объекта;

t₂ - время второго измерения радиальной скорости объекта и расстояния от точки И до объекта;

t - время между первым t₁ и вторым t₂ измерениями значений радиальных скоростей объекта;

а - расстояние от точки И до объекта при первом измерении радиальной скорости объекта Vr₁;

b - расстояние от точки И до объекта при втором измерении радиальной скорости объекта Vr₂;

с - расстояние, пройденное объектом по курсу, за время t;

abc - треугольник, образованный расстояниями a, b и c.

B - угол между направлением первого визирования объекта и его курсом (B>0);

V - курсовая скорость объекта.

Из построений фиг. 1 следует, что:

Из формулы (1) следует, что курсовая скорость объекта V определяется по формуле:

Средняя радиальная скорость объекта за время измерения t равна:

где Vr₁ - радиальная скорость объекта при первом измерении;

Vr₂ - радиальная скорость объекта при втором измерении.

Расстояние с, пройденное объектом по курсу за время t, равно:

где t - время между первым t₁ и вторым t₂ измерениями значений радиальных скоростей объекта.

Для определения курсовой скорости объекта V по формуле (2), определяют значение угла В треугольника abc по известным длинам его сторон a, b и с (фиг. 1) (Бронштейн И.Н. и Семендяев К.А. «Справочник по математике», М., ГИТТЛ, 1954 г., стр. 187).

Обозначим буквой p полупериметр треугольника abc, который равен 0,5(a+b+c). Буквой r обозначим математическое выражение:

Тангенс угла В/2 равен:

Курсовую скорость V объекта по результатам измерения двух значений радиальной скорости определяют по формуле (6), угол В равен 2arctg[r/(p-b)]:

Способ измерения скорости объекта состоит в следующем.

Из точки пространства, вынесенной с курса объекта, производят измерение радиальной скорости объекта и расстояния от вынесенной точки до объекта. Через промежуток времени больше двух секунд, производят второе измерение его радиальной скорости и расстояния от вынесенной точки до объекта. После чего по формуле (4) определяют расстояние, пройденное объектом по курсу за время между первым и вторым измерениями, по формуле (4):

где с - расстояние, пройденное объектом за время t; t - время между измерениями значений первой Vr₁ и второй Vr₂ радиальной скорости объекта. Затем определяют полупериметр p треугольника abc, который равен 0,5(a+b+c), далее по формуле (5):

где r=√(p-a)·(p-b)·(p-c)/p;

а - расстояние от объекта до вынесенной точки, при первом измерении радиальной скорости объекта;

b - расстояние от объекта до вынесенной точки измерения, при втором измерении радиальной скорости объекта;

с - расстояние, пройденное объектом за время t;

p - полупериметр треугольника abc, равный 0,5(a+b+c).

Курсовую скорость V объекта, по результатам измерения двух значений радиальной скорости, определяют по формуле (2), из равенства (6) угол В, между линией первого визирования объекта и его курсом, равен 2arctg[r/(p-b)]:

В качестве устройства для измерений радиальной скорости объекта и расстояния до него может быть использовано устройство по изобретению авт. св. №590687, МПК G01S 13/58, 1976 г. Оно содержит: приемную антенну и последовательно соединенные генератор высокой частоты, фазовый детектор, усилитель постоянного тока и блок управления, выход которого соединен с входом генератора высокой частоты, соединенного с передающей антенной; выход усилителя постоянного тока соединен с входом блока измерения частоты. Устройство также содержит частотно-сдвигающий блок, датчик величины опорной частоты и блок вычитания, второй вход которого соединен с выходом блока измерения частоты.

Также может быть использован способ измерения радиальной скорости движущегося объекта и расстояния до него (Изобретение патент РФ №2535487, G01S 3/58, 2013). Способ состоит в том, что облучают объект сигналом при одновременном приеме в обратном направлении принимаемого сигнала, отраженного от объекта, принятый сигнал фильтруют с помощью фильтра несущей частоты, за отрезок времени (t₂-t₁) измеряют набег фазы ф в принятом сигнале, а радиальную скорость объекта определяют по формуле:

V=ф·λ/4π(t₂-t₁),

где ф - набег фазы в принимаемом сигнале, за время измерения радиальной скорости, который пропорционален расстоянию до объекта; расстояние до объекта L определяют по формуле: L=ф·λ/4π;

λ - длина волны сигнала, облучающего объект;

t₁ и t₂ - моменты времени начала и конца измерения набега фазы.

Пример реализации изобретения по измеренным величинам: Vr₁=0,16 км/сек (576 км/час); Vr₂=0,12 км/сек (432 км/час); Vrcp=0,14 км/сек (504 км/час); t=10 сек; a=5 км, b=4 км, c=t·Vrcp=1,4 км, p=0,5(a+b+c)=5,2 км; r=√(p-a)·(p-b)·(p-c)/p=0,42,

V=Vr₁/cos{2arctg[r/(p-b)]}=0,18 км/сек.

Курсовая скорость объекта V равна 648 км/час, что на 11% больше первой радиальной скорости Vr₁, равной 576 км/час.

Отличительные признаки изобретения

Через промежуток времени больше двух секунд, производят второе измерение его радиальной скорости и расстояния от вынесенной точки до объекта, после чего по формуле (4) определяют расстояние, пройденное объектом по курсу за время между первым и вторым измерениями, по формуле (4):

где c - расстояние, пройденное объектом за время t; t - время между измерениями значений первой Vr₁ и второй Vr₂ радиальной скорости объекта, затем определяют полупериметр p треугольника abc, который равен 0,5(a+b+c), далее по формуле (6):

где r=√(p-a)·(p-b)·(p-c)/p;

а - расстояние от объекта до вынесенной точки, при первом измерении радиальной скорости объекта;

b - расстояние от объекта до вынесенной точки измерения, при втором измерении радиальной скорости объекта;

с - расстояние, пройденное объектом за время t;

p - полупериметр треугольника abc, равный 0,5(a+b+c);

B - угол между линией первого визирования объекта и его курсом, равный 2arctg[r/(p-b)], определяют угол В между линией первого визирования объекта и его курсом, который равен 2arctg[r/(p-b)], а курсовую скорость рассчитывают по формуле (7):

Способ измерения курсовой скорости объекта, состоящий в том, что из точки пространства, вынесенной с курса объекта, производят измерение радиальной скорости объекта и расстояния от вынесенной точки до объекта, отличающийся тем, что через промежуток времени больше двух секунд производят второе измерение его радиальной скорости и расстояния от вынесенной точки до объекта, после чего определяют расстояние, пройденное объектом по курсу за время между первым и вторым измерениями, по формуле:c=t·(Vr₁+Vr₂)/2,где с - расстояние, пройденное объектом за время t; t - время между измерениями значений первой Vr₁ и второй Vr₂ радиальной скорости объекта, затем определяют полупериметр p треугольника abc, который равен 0,5(а+b+с), далее по формуле:tgB/2=r/(p-b),где а - расстояние от объекта до вынесенной точки, при первом измерении радиальной скорости объекта;b - расстояние от объекта до вынесенной точки измерения, при втором измерении радиальной скорости объекта;с - расстояние, пройденное объектом за время t;p - полупериметр треугольника abc, равный 0,5(а+b+с);В - угол между линией первого визирования объекта и его курсом, равный 2arctg[r/(p-b)], определяют угол В между линией первого визирования объекта и его курсом, который равен 2arctg[r/(p-b)],а курсовую скорость V рассчитывают по формуле:V=Vr₁/cos{2arctg[r/(p-b)]}