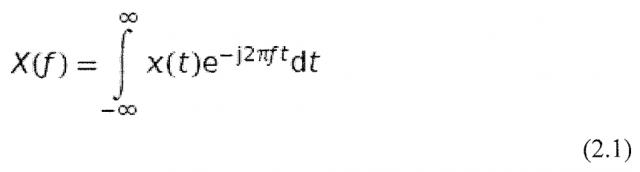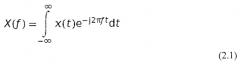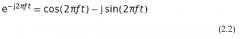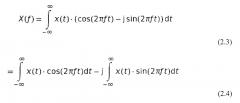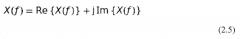Устройство, способ и компьютерная программа для свободно выбираемых сдвигов частоты в области поддиапазонов

Устройство, способ и компьютерная программа для свободно выбираемых сдвигов частоты в области поддиапазонов

Иллюстрации

Показать все

Реферат

Настоящее изобретение относится к обработке аудиосигнала и в частности к устройству, способу и компьютерной программе для произвольных сдвигов частоты в области поддиапазонов.

Автоматизированные системы обработки данных являются неотъемлемой частью повседневной жизни в сегодняшнем обществе, которое характеризуется новыми СМИ. Системы для использования новых СМИ присутствуют почти в каждом домашнем хозяйстве в течение достаточно долгого времени. Примерами таких систем, которые передают и воспроизводят данные в цифровой форме, являются проигрыватели для видеоданных и аудиоданных, например, такие, как проигрыватели для DVD и BluRay, CD и файлов в формате mp3. Эти системы воспроизведения характеризуются воспроизведением мультимедийного контента почти без потерь. Наряду с классической телекоммуникацией, Интернет является важным порталом для связи, например, посредством VoIP. Основополагающая цифровая обработка сигналов характерна для всех упомянутых технологий. Она имеет решающее значение для качества воспроизведения и эффективности цифровых технологий.

Обработка аудиосигнала при этом получает все большее значение. В настоящее время на рынке доступно множество аудио-кодеров, которые реализуются, например, алгоритмами для цифровой обработки аудио материала для его хранения или передачи. Цель каждого способа кодирования заключается в сжатии информационного содержимого сигнала так, чтобы оно занимало по минимуму место в памяти, одновременно сохраняя наилучшее возможное качество воспроизведения. Эффективность современных аудио-кодеров главным образом зависит от требуемой в памяти места и, кроме того, от вычислительной сложности, требуемой для алгоритма.

В основном, кодер цифрового аудио представляет собой инструмент для передачи аудиосигналов в формате, подходящем для хранения или передачи. Это имеет место на передающей стороне аудио-кодера (кодировщик). Данные, произведенные таким образом, затем возвращаются к исходной форме в получателе (декодер) и, в идеальном случае, соответствуют исходным данным, за исключением постоянной задержки. Общей целью аудио-кодеров является минимизация объема данных, требуемого для представления аудиосигнала, одновременно максимизируя воспринимаемое качество воспроизведения. При разработке аудио-кодеров должен быть учтен ряд факторов, таких как, например, точность воспроизведения, скорость передачи данных и сложность. Кроме этого, задержка, прибавляемая за счет обработки сигнала (добавленная задержка), также играет важную роль (Bosi and Goldberg, 2003).

В особенности в начале применения аудиокодирования эффективность способов имела большое значение, так как память и вычислительная производительность были доступны только в очень ограниченной степени. В настоящее время это требование, кажется, имеет меньше значения. Даже домашние PC или ноутбуки в состоянии легко выполнять сложные алгоритмы в режиме реального времени, и широкополосные интернет-соединения обеспечивают достаточную ширину полосы для передачи кодированного аудиоматериала. Тем не менее, усовершенствование способов аудиокодирования имеет особое значение. В области мобильной связи и спутниковой передачи данных ширина полосы является строго ограниченной. Важным является сокращение объема передаваемых данных. Дополнительно к этому, в этой области важна эффективность используемой технологии кодирования. Базовые алгоритмы должны обладать простой структурой для того, чтобы минимизировать вычислительную производительность и потребление энергии.

Другим аспектом является качество воспроизведенных кодированных аудиосигналов. Многие аудио-кодеры уменьшают объем данных, используя сокращение ненужной части сигнала. При этом теряются части сигнала, в зависимости от скорости передачи данных. При низких скоростях передачи данных качество воспроизводимых аудиосигналов уменьшается.

Обычно различают два типа аудиокодирования, а именно, аудиокодирование с потерями и аудиокодирование без потерь. Аудиокодирование без потерь обеспечивает точное восстановление исходного сигнала на стороне получателя. Способ аудиокодирования с потерями, в отличие от этого, вызывает необратимые отклонения от исходного сигнала посредством модели субъективного восприятия (Zölzer, 2005).

Аудиокодирование без потерь основано на сокращении избыточности, содержащейся в кодируемом сигнале. Общепринятым способом здесь является, например, кодирование с линейным предсказанием (LPC) в совокупности с последующим энтропийным кодированием. Такие способы аудиокодирования позволяют точно побитно восстанавливать входной сигнал из кодированного потока битов.

Линейное предсказание использует статистические зависимости между последовательными выборками сигнала для того, чтобы предсказывать будущие значения. Это основано на том факте, что последовательные выборки более подобны друг другу, чем выборки, находящиеся на большем расстоянии друг от друга. Предсказание реализуется фильтром линейного предсказания, который оценивает текущую выборку, используя множество предыдущих выборок. Однако, далее используется не непосредственно эта оценка, которая обработана, а разность между этим значением и фактической выборкой в этом месте. Целью линейного предсказания является минимизация энергии этого сигнала ошибки с помощью оптимизированных фильтров и передача упомянутого сигнала ошибки, что требует лишь небольшой ширины полосы (Weinzierl, 2008).

После этого сигнал ошибки кодируется энтропией. Энтропия представляет собой меру среднего информационного содержания сигнала и указывает на теоретический минимум битов, требуемых для его кодирования. Типичным способом здесь является кодирование методом Хаффмана. Определенные кодовые комбинации связаны здесь с отдельными выборками, в зависимости от статистической вероятности их появления. Короткие символы связаны с часто встречающимися выборками, а редко встречающиеся значения сигнала представлены более длинными кодовыми комбинациями. В среднем, кодированный сигнал таким образом представляется наименьшим возможным количеством битов (Bosi and Goldberg, 2003).

И линейное предсказание, и энтропийное кодирование являются обратимыми, и таким образом не удаляют информацию из сигнала. При комбинировании этих двух способов из кодируемого сигнала удаляется только избыточность. Поскольку такие подходы к кодированию без потерь сильно зависят от характеристик сигнала, выгода от кодирования является сравнительно небольшой. Достигаемый уровень сжатия, то есть отношение скорости передачи битов входного сигнала и скорости передачи кодированного сигнала, находится в области между 1,5:1 и 3:1 (Weinzierl, 2008).

Аудиокодирование с потерями основано на принципе сокращения иррелевантной части информации. Для этих способов требуется модель человеческого восприятия, которая описывает психоакустические явления чувства слуха относительно времени и частотного разрешения. Таким образом, аудиокодирование с потерями также называется кодированием, адаптированным к восприятию, или психоакустическим кодированием. В области аудиокодирования все части сигнала, которые не могут быть восприняты людьми и таким образом являются неслышимыми, упоминаются как ненужные части сигнала (Zölzer, 2005). Чтобы более точно понять режим функционирования аудио кодера, адаптированного к восприятию, очень важно глубокое знание психоакустики.

Человеческий слух анализирует звуковое событие путем разложения его на группы частот. Эти группы частот представляются в шкале Барка, и в англоязычной литературе называются критическими полосами частот. Каждая из этих групп частот суммирует частотный домен, который оценивается человеческим слухом как единое целое. Таким образом, частотный домен соответствует ограниченной области на базилярной мембране. Всего с основной мембраной связано 24 критических полосы частот, ширина полосы которых увеличивается с увеличением частоты (Fastl and Zwicker, 2007). Аудио кодеры с потерями также используют эту модель групп частот для разложения широкополосных сигналов на поддиапазоны и индивидуального кодирования каждой полосы (Zölzer, 2005). Эта модель часто адаптируется, и зачастую вместо шкалы Барка используется линейное частотное деление на более чем 24 полосы.

Другой важной характеристикой слухового восприятия является частотно-зависимое ощущение громкости звуков с равными уровнями звукового давления. Из этого проистекают две особенности слуха. С одной стороны, звуки различных частот, но с равными уровнями звукового давления воспринимаются как имеющие различную громкость, с другой стороны существует частотно-зависимый порог, ниже которого звуки не могут быть восприняты (Fastl and Zwicker, 2007). Этот порог также упоминается как абсолютный порог слышимости или порог слышимости в тишине и проиллюстрирован на Фиг. 22. Из этого могут быть сделаны два вывода для аудиокодирования. Сигналы, уровни которых находятся ниже абсолютного порога слышимости, можно не обрабатывать, так как они все равно не могут быть восприняты. Кроме этого, число этапов квантизации, требуемых на полосу частот, также может быть определено по расстоянию между порогом слышимости в тишине и уровнем сигнала (Zölzer, 2005).

Экранирующие или маскирующие эффекты оказывают самое большое влияние на аудиокодирование. Различают временное и частотно-зависимое маскирование. В обоих случаях, маскирующий сигнал здесь относится к звуковому событию, которое покрывает другое звуковое событие. Таким образом, замаскированное событие становится неслышимым. При временном маскировании покрывается событие, происходящее до или после маскирующего сигнала. Премаскирование не зависит от продолжительности маскирующего сигнала и покрывает звуковые события, происходящие на интервале времени вплоть до 50 мс перед ощущением самого маскирующего сигнала (Yost, 1994). Постмаскирование, напротив, зависит от продолжительности маскирующего сигнала. Звуковые события здесь покрываются после того, как маскирующий сигнал закончился. В зависимости от продолжительности маскирующего сигнала может пройти вплоть до 200 мс, прежде чем слух снова станет способным воспринимать сигналы в диапазоне порога слышимости в тишине (Fastl and Zwicker, 2007).

На Фиг. 21 показана схематичная иллюстрация временного маскирования. В частности на Фиг. 21 схематично показаны области пре- и постмаскирования и соответствующий уровень, ниже которого сигналы маскируются. Временное маскирование может использоваться в аудиокодировании для того, чтобы скрыть побочный шум, вызванный процессом кодирования, такой как, например, шум квантизации, относительно высокоуровневых сигнальных последовательностей (переходные процессы).

Маскирующие эффекты в частотной области играют гораздо более важную роль, чем эффекты временного маскирования. Частотно-зависимое маскирование описывает изменение в пороге слышимости в тишине для отдельных звуков и узкополосного шума. Эти сигналы значительно искажают порог слышимости в тишине из-за их конкретного порога маскирования слышимости. Сигналы, уровень которых меньше, чем порог маскирования слышимости маскирующего сигнала, и которые расположены в эффективном диапазоне упомянутого порога, не могут быть восприняты (Fastl and Zwicker, 2007). Этот контекст проиллюстрирован на Фиг. 22.

На Фиг. 22 показана схематичная иллюстрация частотно-зависимого маскирования в человеческом слухе. Как показано, маскированный звук находится ниже порога маскирования слышимости маскирующего сигнала, и таким образом является неслышимым. Этот эффект используется в способах аудиокодирования с потерями. Части сигнала, находящиеся ниже частотно-зависимого порога маскирования слышимости, удаляются из сигнала и в дальнейшем не обрабатываются (Zölzer, 2005).

Общая схема типичного кодера, адаптированного к восприятию, проиллюстрирована на Фиг. 23. На Фиг. 23 показана блок-схема психоакустического аудио-кодера. Сначала сигнал PCM, подлежащий кодированию, разлагается на полосы частот аналитическим набором фильтров и подается на психоакустическую модель. Здесь зависящий от времени порог маскирования слышимости, который регулирует точность квантизации для различных полос частот, определяется описанными психоакустическими функциями слуха. Таким образом, важные полосы частот, то есть полосы частот, которые легко воспринимаются, квантуются с очень высоким разрешением, а неважные полосы частот представляются с более низким разрешением, т.е. небольшим числом бит. После этого выполняется энтропийное кодирование для уменьшения объема данных, так же, как это делается в аудиокодировании без потерь. Так как дополнительные контрольные параметры должны быть переданы аналитическим набором фильтров и психоакустической моделью, фактический поток битов устанавливается мультиплексором потока битов. Выгода от кодирования в аудио-кодерах с потерями здесь получается за счет комбинирования квантизации и энтропийного кодирования (Zölzer, 2005). В зависимости от того качества, которое должно быть достигнуто, уровень сжатия составляет от 4:1 до 50:1 (Weinzierl, 2008).

Декодер имеет сравнительно простую схему. Сначала полученный поток битов снова делится демультиплексором на сигнальные данные и контрольные параметры. После этого выполняются энтропийное декодирование и обратная квантизация. Контрольные параметры в данном случае управляют обратной квантизацией полезных данных. Сигналы поддиапазона, полученные таким образом, затем подаются на набор фильтров синтеза для того, чтобы восстановить широкополосный сигнал PCM (Zölzer, 2005). Соответствующая блок-схема психоакустического аудио декодера проиллюстрирована на Фиг. 24.

Ниже будет обсужден ряд преобразований сигнала предшествующего уровня техники. Так как квантизация во многих аудио кодерах основана на модели восприятия, которая описывает человеческое восприятие в частотной области, необходимо передавать сигнал, который также будет кодирован в частотной области. Существует большое количество преобразований с различными характеристиками, и областей их применения. Ниже будут представлены преобразования, важные для аудиокодирования, а также будет обсуждена схема набора фильтров.

Преобразование Фурье представляет собой наиболее важный способ для анализа гармонической структуры сигнала. Оно является частью анализа Фурье и названо в честь французского математика и физика Жана-Батиста-Жозефа Фурье (1768-1830), который ввел его первым. Преобразование Фурье представляет собой функцию для преобразования временного сигнала в его представление в частотной области. Оно используется, между прочим, для описания характеристик систем с линейными временными инвариантами (LTI), а также для их предсказания (Burrus and Parks, 1985). Таким образом, оно является, например, очень важным в акустике и в описании человеческого слуха. Основной процедурой преобразования Фурье является разложение временного сигнала на взвешенную сумму косинусоидальных и синусоидальных колебаний. Для апериодических непрерывных сигналов оно вычисляется следующим образом (Bosi and Goldberg, 2003):

.

Здесь x(t) представляет собой сигнал, анализируемый во временной области, а X(ƒ) представляет собой соответствующий спектр Фурье в частотной области. Следует учесть, что результат является комплексным, хотя преобразуется вещественный сигнал. Используя соотношение Эйлера 2.2, можно показать, что вещественная часть X(ƒ) соответствует косинусоидальным членам x(t), а мнимая часть соответствует синусоидальным компонентам. Используя:

уравнение 2.1 принимает вид:

что приводит к:

.

Так как синус и косинус отличаются друг от друга только их фазой, фаза сигнала может быть получена из отношения соответствующих членов. Используется следующая формула:

.

Таким образом, упоминается как абсолютное значение частотной характеристики, а φ(ƒ) упоминается как фазово-частотная характеристики или просто как фаза.

С помощью обратного преобразования Фурье (уравнение 2.9) преобразованный сигнал снова преобразуется к его исходному представлению во временной области. Следует учесть, что преобразование Фурье и обратное преобразование Фурье отличаются друг от друга постоянным коэффициентом и знаком экспоненциальной функции (Burrus and Parks, 1985).

.

Дискретное преобразование Фурье будет обсуждено ниже более подробно.

На практике проблемы возникают в цифровых компьютерах при использовании преобразования Фурье. С одной стороны, это происходит вследствие того, что только конечное число временных значений может быть обработано, а с другой стороны частотная переменная также должна быть представлена дискретно, кроме переменной времени. Решением этих проблем является дискретное преобразование Фурье (DFT). При использовании DFT конечный дискретно-временной сигнал преобразуется в дискретный периодический спектр. Это означает, что DFT представляет собой одно из самых важных преобразований в цифровой обработке сигналов. Источником DFT является преобразование Фурье, точный вывод может быть найден в публикации (Lochmann, 1990). DFT дискретно-временного сигнала x[n] длины N определяется следующим образом (Burrus and Parks, 1985):

.

По аналогии, обратное дискретное преобразование Фурье (IDFT) выглядит следующим образом:

где комплексный вращающийся фазор W:

Таким образом, X[k] является дискретным периодическим спектром сигнала x[n], где . Длина периода спектра соответствует длине преобразования N, а нормализованные частоты отображаются на интервал [0,2π].

Для реальных входных сигналов DFT имеет важную особенность. Здесь вычисляется не N независимых частотных коэффициентов, как это имеет место в общем случае, но только их половина. Эта особенность может быть использована, например, для хранения или передачи данных. Для повторного преобразования вторая половина из N/2 значений вычисляется с использованием следующей корреляции (Rao and Yip, 2001):

Оператор * в уравнении 2,13 характеризует комплексное сопряжение. Таким образом, X(k]* является комлексно сопряженной последовательностью значений для X(k].

Вычислительная сложность DFT и IDFT составляет N² комплексных умножений и сложений. Когда при вычислениях используются симметрии, количество необходимых шагов вычисления сокращается до , и сложность соответствует . Однако при использовании быстрых способов длина преобразования N должна соответствовать степени двух. Быстрое преобразование Фурье обычно упоминается как FFT (Kiencke and Jäkel, 2005).

Дискретное преобразование Фурье не получило распространения в области сжатия данных. Большими недостатками DFT являются высокая вычислительная сложность и избыточность, содержащаяся в спектре. Хотя существуют эффективные способы для того, чтобы вычислить DFT, то есть FFT, результатом всегда будет комплексный спектр. Это означает, что N пар комплексных значений вычисляются из N значений преобразования. В дополнение к этому, только первые N/2 спектральных значений содержат новую информацию.

Дискретные синусоидальное и косинусоидальное преобразования будут обсуждены ниже.

Дискретное косинусоидальное преобразование (DCT) является решением для упомянутых выше проблем DFT. DCT представляет собой вещественное, дискретное, линейное и ортогональное преобразование. Благодаря этим особенностям оно является наиболее часто используемым преобразованием в сжатии цифровых данных (Britanak et al., 2007).

DCT представляет собой дискретное тригонометрическое преобразование. В целом различают восемь форм DCT. В зависимости от их граничного продолжения они делятся на четные и нечетные преобразования, а также на типы I, II, III и IV. Однако для цифровой обработки сигналов важны лишь четные типы DCT. Они перечислены ниже (Rao and Yio, 2001):

Каждая из этих форм имеет свое специальное применение в кодировании. DCT-II используется главным образом в качестве преобразования данных изображения. Литература рассматривает его как первый тип описанного DCT. Это означает, что обычно термин «DCT» относится к DCT-II (Ahmed et al., 1974). За исключением предварительного коэффициента DCT-III представляет собой обратное к DCT-II преобразование, и наоборот. Для аудиокодирования особое значение имеет преобразование DCT-IV. Оно является основой модифицированного дискретного косинусоидального преобразования.

Для того, чтобы можно было продемонстрировать важные особенности DCT, далее будет указана корреляция между DFT и DCT. Как было проиллюстрировано ранее, DFT вычисляет только N/2 независимых частотных коэффициентов из вещественных значений сигнала длины N. И наоборот, это означает, что 2N значений во временной области необходимы для того, чтобы получить N спектральных значений. Однако, если доступны только N временных значений, то сигнал должен быть подходящим образом продолжен. Симметричное расширение за счет зеркального отражения всего сигнала кажется здесь подходящим. Расширенный сигнал таким образом повторяет сам себя с длиной периода 2N. Это имеет то преимущество, что подавляется эффект побочных наводок преобразования DFT с отсеченными сигналами (Kiencke and Jäkel, 2005).

Любой вещественный сигнал x[n] длины N расширяется симметрично, давая в результате:

где Длина таким образом равна 2N. Затем к этому сигналу применяется DFT из уравнения 2.10 с уравнением 2.12 и конвертируется (Rao and Yip, 2001). Подробный вывод может быть найден в приложении А.1. Используются следующие формулы:

Сравнивая этот результат с DCT-II в уравнении 2.14b, можно видеть, что эти два уравнения отличаются только фазовым членом . Так как он является независимым от сигнала и не содержит информации, им можно пренебречь при вычислении DCT (Rao and Yip, 2001). Для DCT-I можно показать подобную корреляцию, но с использованием другого продолжения сигнала x[n]. DCT-IV тогда получается из фазового вращения основной функции DCT-II. Подробный вывод этого может быть найден в публикации (Rao and Yip, 2001).

Из этого результата могут быть сделаны некоторые выводы. Сначала можно заметить, что DCT, в отличие от DFT, является чисто вещественным преобразованием. Из этого следуют два преимущества. Во-первых, для вычислений не нужно выполнять никаких комплексных умножений и сложений, а во-вторых, только половина места в памяти требуется для хранения данных, так как нет никаких комплексных пар значений. Кроме того, поразительно, что DCT требует точно N значений для преобразования, т.е. для вычисления N независимых частотных коэффициентов. Все частоты находятся в интервале [0,π]. В отличие от DFT, обратилась в нуль избыточность, содержащаяся в спектре для вещественных значений входных сигналов, исчезает, и таким образом частотное разрешение становится вдвое выше. Однако недостатком является то, что спектр DCT не может быть преобразован относительно абсолютного значения (или амплитуды) и фазы. Дополнительно к этому может возникнуть такая ситуация, что частоты, которые соответствуют основным функциям DCT (см. уравнения 2.14a-2.14d), но повернуты относительно них по фазе на 90°, содержатся в сигнале. Эти частоты не формируются DCT, то есть соответствующий коэффициент DCT равен нулю. По этим причинам DCT хорошо подходит для эффективного и быстрого сжатия данных, но меньше подходит для анализа сигнала (Malvar, 1992).

Кроме дискретного косинусоидального преобразования, существует дискретное синусоидальное преобразование (DST). В целом различают восемь форм DST. Здесь важным является только DST-IV. Что касается его формы и функций, они соответствуют преобразованию DCT-IV (Rao and Yip, 2001):

Когда сигнал преобразуется с использованием и DCT-IV, и DST-IV, комплексный спектр, сформированный комбинацией двух вещественных спектров, снова содержит информацию об абсолютном значении и фазе. Частотное разрешение здесь все еще является вдвое более высоким, чем в DFT, что означает, что частоты N отображаются на интервал [0,π] (Malvar, 1992).

Для обработки длительных аудиосигналов невозможно преобразовать сигнал в целом. С одной стороны, вычислительная сложность здесь чрезвычайно увеличивается, так как для того, чтобы вычислить DCT требуется также N² вычислительных операций. С другой стороны, обработать сигнал в режиме реального времени невозможно, так как необходимо все время ожидать передачи всего потока данных до тех пор, пока сигнал не сможет быть восстановлен. Следовательно, сигнал необходимо делить на блоки. В этом случае DCT применяется как так называемое блочное преобразование (Rao and Yip, 2001). Используя индекс блока , из уравнения 2.14d получается следующее уравнение для DCT-IV:

Длина сигнала x[n] соответствует bN. При блочном преобразовании возникают блочные артефакты из-за квантизации. Известным примером, где артефакты этого вида могут быть распознаны, является способ сжатия JPEG. Блочные артефакты происходят из граничных продолжений, выполняемых для периодизации. Они не соответствуют первоначально принятым сигнальным продолжениям (см. уравнение 2.16). Результатом являются скачки на границах блока, которые в частотном домене смещают энергию к высоким частотам (Malvar, 1992). Скачки в аудиосигнале могут быть восприняты как потрескивания. Человеческий слух очень чувствителен к таким артефактам. Таким образом, их следует абсолютно избежать.

Далее будет обсуждено модифицированное дискретное косинусоидальное преобразование.

Модифицированное дискретное косинусоидальное преобразование (MDCT) является центральным преобразованием для аудио сжатия. Оно используется, среди прочего, в алгоритмах mp3, AAC и Dolby Digital (ac-3). MDCT представляет собой вещественное, дискретное, линейное и ортогональное преобразование и является модификацией DCT-IV. Оно определяется следующим образом (Rao and Yip, 2001):

Преимуществом MDCT по сравнению с DCT-IV является то, что оно избегает блочных артефактов. Это может быть достигнуто главным образом наложением друг на друга нескольких последовательных блоков. Этот вид преобразования также известен как перекрывающееся ортогональное преобразование (LOT) (Malvar and Staelin, 1989).

Избыточность может быть снова удалена способом перекрытия - добавления (OLA). Таким образом, блоки, формирующиеся в обратном преобразовании, перекрываются до 50% и складываются, эта процедура упоминается как перекрытие - добавление.

Частотное разрешение MDCT может быть дополнительно улучшено путем взвешивания входной последовательности x[n+bN] с помощью оконной функции. В уравнении 2.20 окно соответствует прямоугольной функции, вырезающей текущий блок b из полного сигнала. В частотной области это соответствует свертке (сворачиванию) с использованием функции интегрального синуса. Плохое затухание функции интегрального синуса на границе окна может быть улучшено путем адаптации этой функции окна, и таким образом может быть достигнута увеличенная частотная селекция. Для того, чтобы преобразование MDCT было способно на качественное восстановление, оконная функция w[n] длины 2N должна выполнять условия Принсена-Брэдли (PR) (Princen et al., 1987):

.

Простое окно, выполняющее эти условия и показывающее достаточное затухание на границе окна, является синусом половины волнового окна. Это используется, среди прочего, в алгоритмах mp3 и AAC, и определяется следующим образом (Malvar, 1992):

Путем вставки функции окна в уравнение 2.20 может быть получена другая важная функция MDCT. Результат соответствует дискретной свертке x[n+bN] использующей модулированную функцию окна . Таким образом, поскольку , получается следующее (Schuller and Smith, 1996):

Таким образом, MDCT не может рассматриваться только как блочное преобразование, но также и как модулируемый набор фильтров (Malvar, 1992). Таким образом, оконная функция соответствует низкочастотному прототипному фильтру FIR, который модулируется ядром косинуса и таким образом представляет полосы частот набора фильтров. Результатом этого является то, что входная последовательность x[n+bN] разлагается точно на N поддиапазонов. В соединении с особенностью TDA MDCT выполняет предварительные условия так называемого «критически дискретизированного набора фильтров».

Такой критически дискретизированный набор фильтров проиллюстрирован на Фиг. 25. В частности, на Фиг. 25 показан критически дискретизированный набор фильтров PR с количеством полос N с системной задержкой из n_d отсчетов. Такие наборы фильтров имеют особое значение для аудиокодирования, так как они описывают сигнал настолько точно и полно, насколько это возможно при самом маленьком количестве отсчетов (Rao and Yip, 2001).

Символ соответствует уменьшению скорости оцифровки с коэффициентом 1/N, а - увеличению с коэффициентом N. Сигнал после набора фильтров синтеза идентичен входному сигналу x[n] перед аналитическим набором фильтров, за исключением постоянной задержки из n_d отсчетов. В случае MDCT, представляет собой модулированную оконную функцию Поскольку выполняет условия PR, аналитические фильтры h_k идентичны фильтрам синтеза g_k.

С математической точки зрения это является подходящим для того, чтобы сформулировать системы линейных уравнений, включающие в себя все преобразования, упомянутые до сих пор, в векторно-матричной системе обозначений. Сигнал x[n] длины bN представляется как вектор-столбец . Оператор Т здесь обозначает транспонирование. Формирование блока может быть представлено как матрица, в которой каждый столбец матрицы содержит блок x[n]:

Правило преобразования также может быть представлено в виде матрицы. Модулированные оконные функции здесь формируют строки матрицы. При получается следующее:

.

Для того, чтобы можно было вычислить MDCT , блочная структура должна быть расширена 50%-ым перекрытием для TDA. Таким образом, MDCT может быть записано следующим образом:

где:

Каждый столбец образует спектр MDCT соответствующего блока с номером b в .

Для того, чтобы вычислить блок, эта форма MDCT требует 2N² умножений и сложений. Однако вычислительная сложность может быть значительно уменьшена.

Таким образом, необходимо преобразовать набор фильтров, изображенный на Фиг. 25, к эквивалентному многофазному набору фильтров (см. Фиг. 26). Используя многофазное представление и z-преобразование, многоскоростные системы, такие как набор фильтров MDCT, могут быть проанализированы более широко.

Фильтр FIR h[n] всегда может быть поделен на фаз, когда длина фильтра является кратной М. m-я фаза p_m[n] фильтра h[n] получается путем задержки n[n] на z^-m и уменьшения скорости оцифровки в М раз. (Malvar, 1992). Используется следующая формула:

Используя разложение и z-преобразование, фильтр h[n] может быть представлен следующим образом (Malvar, 1992):

Вместо записи в виде сумм предпочтительной является векторная система обозначений. Уравнение 2.30 таким образом может быть представлено как вектор размерности N:

где:

Это многофазное разложение затем может быть применено к каждому фильтру из набора фильтров MDCT. Результатом является эквивалентное многофазное представление набора фильтров, упомянутого выше, изображенное на Фиг. 26 (Schuller and Smith, 1996). Таким образом, Фиг. 26 представляет эквивалентный критически дискретизированный многофазный набор фильтров PR с количеством полос N.

Используя симметрии в ядре MDCT и особенность TDA, анализ и синтез матриц многофазных фильтров и может каждый быть разделен на разреженную матрицу свертки и матрицу преобразования (Schuller and Smith, 1996). Матрицы свертки и здесь имеют ромбовидную структуру с коэффициентами оконной функции в виде полиномиалов в z-области. Они могут быть далее разложены на матрицу окна и матрицу задержки:

Точная форма и разбиение матриц свертки будут показаны ниже. Матрицы преобразования соответствуют матрице DCT-IV:

Используя эти матрицы, спектр MDCT входного сигнала, разделенного на блоки , вычисляется следующим образом (Schuller and Smith, 1996):

где для обратного преобразования применяется следующая формула:

Это решение предлагает несколько преимуществ по сравнению с вычислением MDCT в соответствии с уравнением 2.26. Во-первых, формирование искажений за счет эффекта наложения во временной области может быть более легко распознано. При многофазном представлении матрицы свертки в уравнении 2.33a процесс может быть интерпретирован как переворачивающий взвешенные части сигнала блока (b-1) в текущий блок b. Путем добавления этих частей сигнала образуется TDA. Самым большим преимуществом вычисления MDCT с использованием множества фаз является значительно уменьшенная вычислительная сложность. При использовании квадратной матрицы DCT-IV и разреженной матрицы свертки вычислительная сложность уменьшается до N(N+2) умножений и сложений. Путем использования быстрых реализаций DCT, аналогично FFT, количество требуемых операций может быть сокращено вплоть до N(logN+2), и таким образом сложность может быть уменьшена до (Rao and Yip, 2001). По этим причинам в настоящем документе предполагается реализация MDCT в соответствии с многофазным подходом.

При обработке аудиосигнала