Моделирование температуры, ограниченное геофизическими данными и кинематическим восстановлением

Моделирование температуры, ограниченное геофизическими данными и кинематическим восстановлением

Иллюстрации

Показать все

Реферат

ОБЛАСТЬ ТЕХНИКИ

Настоящее изобретение относится к моделированию температуры, ограниченному геофизическими данными и кинематическим восстановлением и, в частности, настоящее раскрытие относится к моделированию температуры и ограничению таких моделей на основании анализа скорости сейсмической волны, инверсии силы тяжести, физики горных пород, структурной геологии и вычислительной математики.

УРОВЕНЬ ТЕХНИКИ

В области разведочной геофизики исследование подземных структур и свойств геологической среды и эволюции этих свойств на протяжении шкал геологического времени является основным предметом.

В настоящее время имеются несколько коммерческих пакетов программного обеспечения для моделирования бассейнов:

Документация на программное обеспечение PetroMod, Schlumberger.

Документация на программное обеспечение PerMedia, Landmark.

Документация на программное обеспечение Temis, Institut Français Pétrole (IFP).

Способы, реализуемые в известных коммерческих пакетах программного обеспечения, не ограничены геофизическими данными и горнофизическими моделями, и в них не применяется стратегия обновления в зависимости от несовпадения с геофизическими наблюдениями.

В настоящее время отсутствуют способы моделирования, в которых эти проблемы учитываются в достаточной степени и особенно с упором на понимание эволюции температур и температурных градиентов на протяжении шкал геологического времени.

КРАТКОЕ ИЗЛОЖЕНИЕ ИЗОБРЕТЕНИЯ

Информация относительно температуры и, в частности, эволюции температуры и температурных градиентов потока в данном бассейне на протяжении шкал геологического времени является центральным моментом при определении, преобразовалось ли органическое вещество материнской породы в углеводород.

Настоящее изобретение применимо во всех областях моделирования геологической среды и при разведке, в том числе на нефть и газ. Данными из способов измерений, такими как сейсмические, магнитные и гравитационные аномалии, температура в скважине, данные кернового анализа и другие, могут предоставляться важные параметры, но в лучшем случае может даваться только частичная картина истинного характера представляющих интерес геологических свойств среды. Кроме того, моделирование само по себе сильно зависит от используемых параметров и от того, насколько хорошо они понимаются. При ограничении моделей данными измерений модели могут обеспечивать более точное кинематическое восстановление на протяжении шкал геологического времени для представляющей интерес геологической структуры.

Термин «кинетическое восстановление» обычно обозначает полученную моделированием реконструкцию геологической структуры, предпочтительно с помощью трехмерной модели, в которой имитируется последовательность промежуточных стадий между недеформированным и деформированным состояниями.

В дополнение к этому способы обработки данных и визуализации, основанные на моделях с ограниченными данными, сильно зависят от пространственного охвата и качества используемых входных данных.

Геологическая история и прошлые и настоящие распределения температур непосредственно связаны с текущими геофизическими наблюдениями в трех измерениях.

Настоящим изобретением разрешаются основные проблемы, связанные с оцениванием нефтегазоносных систем, и оно выходит за рамки известного в настоящее время программного обеспечения и передовых практических способов. Изобретением обеспечивается снижение неопределенности при моделировании температуры благодаря ограничению концептуальных моделей бассейна на основании геофизических наблюдений.

Первый аспект настоящего изобретения относится к способу оценивания распределений температур по геологической среде на основании трехмерной модели теплопроводности для геологического пласта, характеризующемуся следующими этапами:

а) получение измеренных данных, соответствующих представляющему интерес геологическому подземному пласту, содержащих данные сейсмических исследований, внутрискважинную температуру, измерения теплового потока на дне или поверхности моря и лабораторные измерения пористости керна,

b) оценивание зависимости между скоростью сейсмической волны и теплопроводностью, при этом скорость сейсмической волны линейно зависит от пористости и теплопроводность экспоненциально или линейно зависит от пористости, и

с) калибровка указанной модели по указанным измеренным внутрискважинным данным и лабораторным измерениям пористости керна.

Второй аспект настоящего изобретения относится к способу из первого аспекта, в котором указанную скорость сейсмической волны оценивают с помощью инверсии Дикса, или анализа скорости при глубинной миграции до суммирования (ГМДС), или полноволновой инверсии.

Третий аспект настоящего изобретения относится к способу из первого или второго аспекта, в котором распределения температур по геологической среде оценивают путем решения дифференциального уравнения на базе основного закона теплопроводности Фурье:

q=-k·∇T,

где q - вектор теплового потока,

k - теплопроводность и

∇ T   =   ( ∂ T ∂ x , ∂ T ∂ y , ∂ T ∂ z ) - температурный градиент.

Четвертый аспект настоящего изобретения относится к способу из третьего аспекта, в котором граничные условия для решения уравнения на базе основного закона теплопроводности Фурье основаны на следующих этапах:

а) создание геологических сценариев на основании интерпретации сейсмических данных, включающих глубину до границы Мохоровичича,

b) наложение ограничений на набор геологических сценариев с использованием гравиметрических и магнитных данных,

с) вычисление решений для конечных членов уравнения на базе основного закона теплопроводности Фурье в предположения ряда ситуаций, связанных с постоянным тепловым потоком, для каждой ситуации,

d) калибровка ряда решений уравнения на базе основного закона теплопроводности Фурье по внутрискважинным температурным измерениям и измерениям теплового потока на поверхности или дне моря, предпочтительно в рамках статистической основы Байеса, и

е) вычисление равновесного распределения температур на основании отображения V<=>|q/k|.

Пятый аспект настоящего изобретения относится к способу из четвертого аспекта, в котором указанное распределение температур представляет собой распределение температур на сегодняшний день, предназначенное для использования в качестве конечного условия в прямой модели истории температуры как функции геологического времени.

Шестой аспект настоящего изобретения относится к способу из четвертого аспекта, в котором указанное распределение температур представляет собой распределение температур на сегодняшний день, предназначенное для использования в качестве начального условия в обратной модели истории температуры как функции геологического времени.

Седьмой аспект настоящего изобретения относится к способу из пятого или шестого аспекта, в котором конечноразностные и конечноэлементные решения используют в уравнениях диффузии тепла для теплового потока.

Восьмой аспект настоящего изобретения относится к способу из седьмого аспекта, в котором для указанных имитаций теплового потока используют следующие параметры:

а) теплопроводность, в том числе анизотропную теплопроводность,

b) адвекцию, включающую поднятие, и опускание, и конвекцию, включающую поток текучей среды,

с) внешние граничные условия, включающие измеренную температуру, температурный градиент или тепловой поток в верхней части и основании,

d) выделение внутренней теплоты, включающее радиоактивный распад в осадках,

е) нестационарные источники теплоты, в том числе внедрения, и

f) зависящие от времени свойства геологической среды, в том числе известную геологическую историю.

Девятый аспект настоящего изобретения относится к способу из восьмого аспекта, в котором моделирование истории геологической температуры проводят итерационным методом, выполняя следующие этапы:

а) предположение относительно конечного члена и средних ситуаций для ряда геологических историй с помощью кинематического восстановления, включающего геологические события первого порядка, такие как опускание, поднятие, эрозия, оледенение, основные тектонические события,

b) построение соответствующих зависящих от времени моделей свойств для теплопроводности, теплоемкости и массовой плотности с использованием горнофизических моделей и геофизических данных, включающих скорость сейсмической волны и силу тяжести,

с) прямое моделирование или обратное моделирование истории температуры при использовании ряда граничных условий, включающих зависящий от времени тепловой поток или температуру в верхней части и основании,

d) сравнение полученной прямым моделированием температуры и истории температурного градиента с прогнозным, существующим на сегодняшний день распределением температур,

е) коррекция указанных граничных условий с использованием степени несовпадения для отказа от маловероятных геологических историй,

f) коррекция указанных граничных условий при использовании автоматической процедуры инверсии для согласования с существующим на сегодняшний день распределением температур.

Десятый аспект настоящего изобретения относится к способу из девятого аспекта, в котором выходные данные численных имитаций содержат историю температуры в одном измерении, двух измерениях или трех измерениях и историю температурного градиента.

КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ

Фигура 1 - иллюстрация зависящих от времени геофизических свойств, связанных с геологической историей;

фигура 2 - иллюстрации полученной прямым моделированием температуры (слева) и истории температурного градиента (справа) при граничных условиях Т=0°С в верхней части и Т=800°С в нижней части;

фигура 3а - иллюстрация истории полученной прямым моделированием конечной (существующей на сегодняшний день) температуры спустя 120 миллионов лет;

фигура 3b - иллюстрация истории полученного прямым моделированием конечного (существующего на сегодняшний день) температурного градиента спустя 120 миллионов лет; и

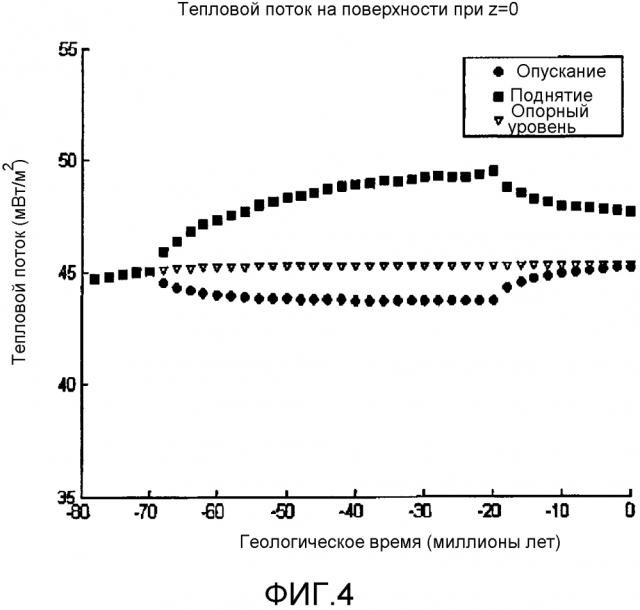
фигура 4 - иллюстрация полученного прямым моделированием теплового потока на поверхности как функции геологического времени, вычисленного на основании полученного прямым моделированием температурного градиента и теплопроводности в соответствии с основным законом теплопроводности Фурье.

ПОДРОБНОЕ ОПИСАНИЕ ИЗОБРЕТЕНИЯ

Сочетание нижеследующих элементов, таких как анализ скорости сейсмической волны, инверсия магнитных и гравиметрических данных, горнофизическая модель, структурные геофизические модели, численное моделирование и электромагнитные данные, образует ключевые признаки изобретения.

Уравнение (диффузии) теплового потока (в том числе адвекции и конвекции) связывают с плотностью через силу тяжести и к тому же связывают со скоростью сейсмической волны через посредство горнофизической модели. Это приводит к образованию зависимости между теплопроводностью и скоростью сейсмической волны.

Различные исторические сценарии могут быть включены в моделирование. Ключевым элементом является широкое использование уравнений диффузии тепла для моделирования истории температуры на основании геологической истории и соответствующих зависящих от времени геофизических свойств, в соответствии с которыми образуют модель, объясняющую современные геофизические и температурные данные наблюдений, включающие непосредственные температурные измерения в скважинах и теплового потока на дне или поверхности моря.

Ключевыми элементами настоящего изобретения являются следующие:

1) ОПРЕДЕЛЕНИЕ ТРЕХМЕРНЫХ КУБОВ СУЩЕСТВУЮЩЕГО НА СЕГОДНЯШНИЙ ДЕНЬ РАСПРЕДЕЛЕНИЯ ТЕМПЕРАТУР ПО ГЕОЛОГИЧЕСКОЙ СРЕДЕ:

В предположении теплового равновесия распределение температур можно вычислить путем решения дифференциального уравнения, составленного на базе основного закона теплопроводности Фурье q=-k·∇T, где q - тепловой поток, k - теплопроводность и ∇ T   =   ( ∂ T ∂ x , ∂ T ∂ y , ∂ T ∂ z ) - температурный градиент.

Трехмерная модель теплопроводности будет построена при использовании горнофизических зависимостей между скоростью сейсмической волны и теплопроводностью. Поэтому при наличии интервальных скоростей сейсмических волн из инверсии Дикса, анализа скорости при глубинной миграции до суммирования (ГМДС) или полноволновой инверсии можно построить и прокалибровать по скважинным данным трехмерную модель удельной проводимости, содержащую непосредственные данные о температуре и результаты лабораторных измерений кернов, предназначенные для получения пористости керна.

Общая зависимость между скоростью сейсмической волны и теплопроводностью представляет собой линейно-экспоненциальное соотношение, то есть скорость является линейной функцией пористости, тогда как удельная проводимость является экспоненциальной функцией пористости. Кроме того, в первом приближении удельную проводимость можно аппроксимировать линейной функцией пористости. Часть изобретения относится к уточнению и калибровке горнофизических моделей, описывающих эту зависимость.

Основная задача заключается в определении граничных условий для решения уравнения на базе основного закона теплопроводности Фурье. Для решения этой задачи можно выполнить следующее:

1. Создать геологические сценарии на основании интерпретации сейсмических данных, включающих глубину до границы Мохоровичича (Мохо).

2. Наложить ограничения на набор геологических сценариев с использованием гравиметрических и магнитных данных.

3. Вычислить решения для конечных членов уравнения на базе основного закона теплопроводности Фурье в предположении ряда ситуаций, связанных с постоянным тепловым потоком (для каждой ситуации).

Ряд решений уравнения на базе основного закона теплопроводности Фурье следует прокалибровать по температурным измерениям в скважинах и измерениям теплового потока на поверхности. Это можно естественным образом описать в рамках статистической основы Байеса.

С математической точки зрения основной закон теплопроводности Фурье имеет такую же структуру, как уравнение эйконала в теории сейсмических лучей для распространения волн ( |   ∇ τ   |   =   1 V ) , где τ обозначает время пробега волны и V обозначает скорость волны. Поэтому равновесное распределение температур можно вычислить в соответствии с отображением V<=>|q/k|.

2) ЗАВИСЯЩЕЕ ОТ ВРЕМЕНИ МОДЕЛИРОВАНИЕ ТЕМПЕРАТУРЫ, ОГРАНИЧЕННОЕ ГЕОФИЗИЧЕСКИМИ НАБЛЮДЕНИЯМИ И ГЕОЛОГИЧЕСКОЙ ИСТОРИЕЙ

При использовании существующего на сегодняшний день распределения температур в качестве конечного условия (или начального условия) выполняют прямое моделирование (или обратное моделирование) истории температуры как функции геологического времени. Для этого следует получить конечноразностные и конечноэлементные решения диффузионного уравнения для теплового потока.

Следующие зависящие от времени эффекты учитываются при имитации теплового потока:

а) Теплопроводность, в том числе анизотропная теплопроводность.

b) Адвекция (поднятие, опускание) и конвекция (поток текучей среды).

с) Внешние граничные условия (температура или тепловой поток в верхней части или основании).

d) Выделение внутренней теплоты (радиоактивный распад в осадках).

е) Нестационарные источники теплоты (например, внедрения).

f) Зависящие от времени свойства геологической среды (например, геологическая история).

Ключевым элементом при моделировании истории температуры является реконструкция геологической истории.

Итерационный метод используется в указанной ниже последовательности:

Предположение относительно конечного члена и средней ситуации для ряда геологических историй с помощью кинематического восстановления, включающего геологические события первого порядка (опускание, поднятие, эрозию, оледенение, основные тектонические события).

Построение соответствующих зависящих от времени моделей свойств для теплопроводности, теплоемкости и массовой плотности с использованием горнофизических моделей и геофизических данных (скорости сейсмической волны и силы тяжести).

Прямое моделирование (или обратное моделирование) истории температуры при использовании ряда граничных условий. Граничные условия задаются в зависимости от температуры, температурных градиентов или теплового потока в верхней части или основании модели.

Сравнение полученной прямым моделированием температуры и истории температурного градиента с прогнозным существующим на сегодняшний день распределением температур.

Использование степени несовпадения с изложенным выше для коррекции граничного условия или для отказа от маловероятных геологических историй. Коррекцию граничных условий можно выполнять как ручную процедуру или как автоматическую процедуру инверсии.

Выходными данными численной имитации являются история температуры в одном измерении, двух измерениях или трех измерениях и история температурного градиента, непосредственно связанная с геологической историей (в том числе с опусканием, поднятием, сетчатой эрозией и переходными событиями).

Фигура 1. Зависящие от времени геофизические свойства, связанные с геологической историей. В первом приближении отложение, опускание и поднятие подчиняются систематическим трендам, подконтрольным пористости и литологии. Зависящая от времени теплопроводность при опускании (слева) и поднятии (справа). Обычно теплопроводность, скорость сейсмической волны, плотность и удельное сопротивление содержат в себе «память» относительно максимальной глубины захоронения. Значения теплового потока вблизи нижней части графиков соответствуют наибольшим значениям по шкале, тогда как значения теплового потока вблизи верхней части графиков соответствуют наименьшим значениям по шкале.

Фигура 2. Полученная прямым моделированием температура (слева) и история температурного градиента (справа) при граничных условиях Т=0°С в верхней части и Т=800°С в нижней части. Вычисления выполнены с использованием конечноразностного решения нестационарного уравнения теплового потока. Конечное состояние (черная кривая) и распределение температур шагами по 10 миллионов лет (тонкие серые кривые).

Фигура 3а. Полученные прямым моделированием конечные истории температуры (существующие на сегодняшний день) на глубине 2,5 км спустя 120 миллионов лет с показом опускания, поднятия и постоянного опорного уровня.

Фигура 3b. Полученные прямым моделированием конечные истории температурного градиента (существующие на сегодняшний день) на глубине 2,5 км спустя 120 миллионов лет с показом опускания, поднятия и постоянного опорного уровня.

Фигура 4. Полученный прямым моделированием тепловой поток (мВт/м²) на поверхности как функция геологического времени, вычисленный на основании полученного моделированием температурного градиента и теплопроводности в соответствии с основным законом теплопроводности Фурье. (1) обозначает момент, в который опускание/поднятие начинается, (2) обозначает момент, в которой опускание/поднятие прекращается, и (3) обозначает другое конечное состояние с более высоким тепловым потоком, обусловленным перемещением вверх горной породы с высокой проводимостью и эрозией более молодой горной породы с низкой проводимостью.

В заключение, новыми элементами последовательности действий являются:

- Использование результатов измеренных геофизических наблюдений для наложения ограничений на моделирование температуры.

- Совместные ограничения на основании кинематического восстановления и геофизических наблюдений.

- Получение калиброванных горнофизических моделей, связывающих скорость сейсмической волны и плотность с теплопроводностью.

- Использование существующего программного обеспечения трассирования сейсмических лучей для моделирования распределений температур.

- Использование уравнений полной диффузии тепла для моделирования истории температуры на основании геологической истории и соответствующих зависящих от времени геофизических свойств.

- Формулирование задачи истории температуры в рамках основы Байеса.

Хотя с целью ясного понимания изложенное выше изобретение было описано довольно подробно в качестве иллюстрации и примера, для специалистов в соответствующей области техники совершенно очевидно, что с учетом идей этого изобретения определенные изменения и модификации могут быть сделаны без отступления от объема прилагаемой формулы изобретения.

Хотя изобретение было пояснено и подробно рассмотрено на чертежах и в последующем описании, такое пояснение и рассмотрение следует считать иллюстративным или примерным и не создающим ограничения, а изобретение не предполагается ограниченным раскрытыми вариантами осуществления. То, что некоторые признаки перечисляются во взаимно различных зависимых пунктах формулы изобретения, не означает, что сочетание этих признаков невозможно успешно использовать. Любые позиции в формуле изобретения не следует толковать как ограничивающие объем изобретения.

1. Способ оценивания распределения температур по геологической среде на основании трехмерной модели теплопроводности для геологического пласта, характеризующийся тем, что выполняют следующие этапы, на которых:а) получают измеренные данные, соответствующие представляющему интерес геологическому подземному пласту, содержащие данные сейсмических исследований, внутрискважинную температуру, измерения теплового потока на дне или поверхности моря и лабораторные измерения пористости керна,b) оценивают зависимость между скоростью сейсмической волны и теплопроводностью, при этом скорость сейсмической волны линейно зависит от пористости и теплопроводность экспоненциально или линейно зависит от пористости, ис) калибруют указанную модель по указанным измеренным внутрискважинным данным и лабораторным измерениям пористости керна.

2. Способ по п. 1, в котором указанную скорость сейсмической волны оценивают с помощью инверсии Дикса, или анализа скорости при глубинной миграции до суммирования (ГМДС), или полноволновой инверсии.

3. Способ по п. 1 или 2, в котором распределения температур по геологической среде оценивают путем решения дифференциального уравнения на базе основного закона теплопроводности Фурье:q=-k·∇T,где q - вектор теплового потока,k - теплопроводность и ∇ T   =   ( ∂ T ∂ x , ∂ T ∂ y , ∂ T ∂ z ) - температурный градиент.

4. Способ по п. 3, в котором граничные условия для решения уравнения на базе основного закона теплопроводности Фурье основаны на следующих этапах:а) создание геологических сценариев на основании интерпретации сейсмических данных, включающих глубину до границы Мохоровичича,b) наложение ограничений на набор геологических сценариев с использованием гравиметрических и магнитных данных,с) вычисление решений для конечных членов уравнения на базе основного закона теплопроводности Фурье в предположения ряда ситуаций, связанных с постоянным тепловым потоком, для каждой ситуации,d) калибровка ряда решений уравнения на базе основного закона теплопроводности Фурье по внутрискважинным температурным измерениям и измерениям теплового потока на поверхности или дне моря, предпочтительно в рамках статистической основы Байеса, ие) вычисление равновесного распределения температур на основании отображения V<=>|q/k|.

5. Способ по п. 4, в котором указанное распределение температур представляет собой распределение температур на сегодняшний день, предназначенное для использования в качестве конечного условия в прямой модели истории температуры как функции геологического времени.

6. Способ по п. 4, в котором указанное распределение температур представляет собой распределение температур на сегодняшний день, предназначенное для использования в качестве начального условия в обратной модели истории температуры как функции геологического времени.

7. Способ по п. 5 или 6, в котором конечноразностные и конечноэлементные решения используют в уравнениях диффузии тепла для теплового потока.

8. Способ по п. 7, в котором для указанных имитаций теплового потока используют следующие параметры:а) теплопроводность, в том числе анизотропную теплопроводность,b) адвекцию, включающую поднятие, и опускание, и конвекцию, включающую поток текучей среды,с) внешние граничные условия, включающие измеренную температуру, температурный градиент или тепловой поток в верхней части и основании,d) выделение внутренней теплоты, включающее радиоактивный распад в осадках,е) нестационарные источники теплоты, в том числе внедрения, иf) зависящие от времени свойства геологической среды, в том числе известную геологическую историю.

9. Способ по п. 8, в котором моделирование истории геологической температуры проводят итерационным методом, выполняя следующие этапы:а) предположение относительно конечного члена и средних ситуаций для ряда геологических историй с помощью кинематического восстановления, включающего геологические события первого порядка, такие как опускание, поднятие, эрозия, оледенение, основные тектонические события,b) построение соответствующих зависящих от времени моделей свойств для теплопроводности, теплоемкости и массовой плотности с использованием горнофизических моделей и геофизических данных, включающих скорость сейсмической волны и силу тяжести,с) прямое моделирование или обратное моделирование истории температуры при использовании ряда граничных условий, включающих зависящий от времени тепловой поток или температуру в верхней части и основании,d) сравнение полученной прямым моделированием температуры и истории температурного градиента с прогнозным существующим на сегодняшний день распределением температур,е) коррекция указанных граничных условий с использованием степени несовпадения для отказа от маловероятных геологических историй,f) коррекция указанных граничных условий при использовании автоматической процедуры инверсии для согласования с существующим на сегодняшний день распределением температур.

10. Способ по п. 9, в котором выходные данные численных имитаций содержат историю температуры в одном измерении, двух измерениях или трех измерениях и историю температурного градиента.