Способ измерения дальности цели в ближней радиолокации

Способ измерения дальности цели в ближней радиолокации

Иллюстрации

Показать все

Реферат

Данное изобретение относится к области ближней радиолокации, в частности к радиолокационным станциям (РЛС) ближнего действия, в которых применяются цифровые методы обработки сигналов. К радиолокаторам ближнего действия можно отнести обнаружители заглубленных в грунт объектов или объектов за преградой. Уменьшения затухания радиоволн в среде, как правило, достигают использованием зондирующих сигналов с частотой порядка десятков-сотен мегагерц. Точность определения дальности до цели δr определяется известным отношением элемента разрешения ΔR к отношению сигнал-шум (ОСШ) q [1, с. 65]:

Указанный способ показывает, как повысить точность измерения дальности до цели, не прибегая к расширению полосы сигнала для улучшения разрешающей способности.

При цифровой обработке сигналов вследствие теоремы Котельникова для восстановления принятого эхо-сигнала требуется формирование двух отсчетов цифрового сигнала на элемент разрешения [2, с. 187], то есть , t_d - период дискретизации сигнала, - ширина спектра сигнала. Что является предельным случаем теоремы Котельникова, и координата цели по дальности будет определяться с точностью до элемента разрешения. Как показано в [3, с. 51], использование низкой частоты дискретизации повышает уровень боковых лепестков сжатого в согласованном фильтре эхо-сигнала и ухудшает элемент разрешения по дальности.

Традиционными методами измерения дальности являются измерение по переднему фронту импульса, то есть измерение пересечения передним фронтом импульса некоторого порогового уровня [4, с. 555], либо измерение при использовании селектирующих сигналов и согласованных фильтров [4, с. 556]. Однако данные хорошо известные методы не учитывают особенностей сигналов в РЛС при их дискретизации.

Увеличение точности определения дальности может быть достигнуто применением способов сверхразрешения [например, 5, с. 139-147], однако данные методы требуют знания большого количества априорной информации о сигнале, которая в реальных условиях может отсутствовать.

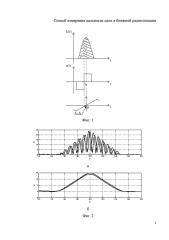
В качестве прототипа заявляемого способа обработки сигналов выбран медианный метод оценки времени задержки сигнала [6, с. 164]. Для реализации данного метода на устройство сравнения подаются функция огибающей сигнала U(t) от цели по дальности и функция двух сомкнутых стробов u(t-t₀), асимметричных по отношению к точке t₀ (фиг. 1). Далее производится сравнение площадей S₁ и S₂ под U(t).

Медианной оценке времени задержки сигнала по дальности соответствует положение t₀, при котором S₁-S₂=0. Недостатком данного метода является уменьшение точности измерения при уменьшении частоты дискретизации принимаемых колебаний в соответствии с обобщенной теоремой Котельникова.

Ранние источники утверждают [7, с. 99], что повысить точность измерения дальности до цели можно, используя информацию, содержащуюся в сигнале высокой частоты. Однако данная информация редко используется из-за возникающей неоднозначности измерений.

Смещение цели относительно РЛС по дальности характеризуется непрерывным изменением фазы сигнала. Изменение фазы принимаемых колебаний на 2π означает, что расстояние до цели изменилось на величину, равную длине волны зондирующего сигнала λ. При цифровой обработке сигнала максимально возможная точность измерения дальности определяется расстоянием Δl, соответствующим периоду дискретизации . То есть , где - частота дискретизации сигнала, причем изменение дальности до цели на расстояние меньшее Δl невозможно отследить. Определить изменение фазы сигнала при его перемещении на расстояние Δl можно, используя соотношение:

где k=2π/λ - волновое число, - центральная частота зондирующего сигнала.

Величина φ_Δl показывает смещение фазы сигнала при изменении задержки отраженного от цели сигнала на dt, при этом сама форма дискретного сигнала также изменится. Фаза принимаемых колебаний определяется расположением цели по дальности. Для измерения дальности до цели с точностью выше Δl сформируем опорный сигнал в дискретные моменты времени, совпадающие с выборками АЦП, огибающая которого повторяет форму огибающей зондирующего сигнала, начальная фаза высокочастотного заполнения с частотой равна 0. Значит, вычисляя разность фаз Δφ опорного сигнала (с нулевой фазой) и сигнала, отраженного от цели, истинное положение которого соответствует временной задержке между двумя соседними дискретными выборками сигнала, можно определить смещение принятого сигнала внутри интервала dt.

Для измерения удобно использовать схему измерения разности фаз Δφ, аналогичную описанной в [8, с. 373], тогда Δφ будет вычисляться по формуле:

где суммирование производится по n дискретным выборкам сигналов, s₁ - опорный сигнал, s₂ - эхо-сигнал от цели, выражение соответствует преобразованию Гильберта сигнала s₂. То есть величина Δφ дает поправку к координате цели по дальности относительно измеренной дальности до цели. Разность фаз Δφ определяет разность хода двух электромагнитных колебаний, длина волны λ которых известна, поэтому поправка к дальности Δr вычисляется по формуле:

.

Техническим результатом является повышение точности измерения дальности цели с помощью вычисления поправки к дальности Δr, позволяющей избежать ошибок, связанных с временной дискретизацией сигнала.

Для обнаружения сигнала по дальности, как правило, используется фильтр, согласованный с опорным сигналом, максимизирующий ОСШ. Рассмотрим преобразование в таком фильтре двух отраженных от цели простых гармонических сигналов, дискретизованных по времени и сдвинутых по фазе относительно друг друга на 50°. Как видно на фиг. 2а, фазовые структуры корреляционных функций данных сигналов с опорным различны, но в результате усреднения данных функций для измерения дальности (фиг. 2б) получим максимумы функций, совмещенные в одной временной выборке, то есть на одной дальности.

Автокорреляционная функция опорного сигнала дает нам сигнал без сдвига на измеренной дальности, относительно которого измеряется поправка Δφ в соответствии с формулой (2). На фиг. 3 показан график зависимости ошибки измерения разности фаз от разности фаз двух сигналов. Как видно из графика, при больших ОСШ ошибка измерения разности фаз незначительна.

В пересчете на поправку Δr с ОСШ=20 дБ (фиг. 4) дисперсия ошибки измерения дальности составляет порядка 0,05 м. Измерение дальности только амплитудным методом по максимуму корреляционной функции при выбранной ширине спектра зондирующего сигнала Δf=30 МГц дает точность измерения, равную δr≈0,5 м, согласно (1). То есть использование измерения разности фаз повышает точность измерения дальности в 10 раз.

Для уточнения координаты цели по дальности фазовым методом необходимо учитывать соотношение размеров одного интервала между дискретными выборками сигнала по дальности и длины волны сигнала. Однозначное измерение фазы возможно при соблюдении условия φ_Δl<π/2, которое, используя соотношение (1), можно переписать в виде:

В случае, когда изменение фазы отраженного от цели сигнала при перемещении на расстояние, соответствующее одной дискретной выборке, превышает π/2, то есть условие (4) не выполняется, могут возникнуть аномально большие ошибки измерения дальности, что проявляется в перескоке фазы на π (фиг. 5). При известных параметрах сигнала максимальная разность фаз при переходе от выборки к выборке вычисляется по формуле (2), что позволяет учитывать подобные ошибки адаптивно.

Таким образом, выбор частоты дискретизации необходимо осуществлять для конкретных параметров сигнала. Рассмотрим зависимость ошибки измерения разности фаз сигналов для выбранной разности фаз, равной 20° от частоты дискретизации (фиг. 6). По данному графику можно определить интервалы частот дискретизации, при которых разность фаз измеряется наиболее точно. Более того, существуют интервалы, на которых измеренная фаза отличается от реальной знаком, то есть при изменении знака аргумента функции arctg() формулы (3), точное измерение фазы сигналов также возможно.

Сохранение фазовой структуры сигнала с целью дальнейшего уточнения координаты цели по дальности возможно при соблюдении условия выбора частоты дискретизации сигнала (4). Данное условие не соответствует условию обобщенной теоремы Котельникова, так как сильное влияние наложения спектров в значительной степени искажает фазовую структуру сигнала. Тем не менее, для частот дискретизации от и более с использованием соответствующей обработки для конкретных параметров сигнала можно смягчить данное условие. В результате, применяя фазовый метод уточнения координаты цели по дальности при больших ОСШ, можно повысить точность измерения дальности в 10 раз по сравнению с медианным методом измерения дальности, что особенно важно при определении координат цели в ближней радиолокации, где требования к точности измерения координат высоки.

Литература:

1. Бартон Д. Радиолокационные системы. М.: Военное издательство, 1967, 480 с.

2. Антипов В.Н., Горяинов В.Т., Кулин А.Н. и др. Радиолокационные станции с цифровым синтезирванием апертуры антенны. М.: Радио и связь, 1988, 304 с.

3. Кузьмин С.З. Основы проектирования систем цифровой обработки радиолокационной информации. М.: Радио и связь, 1986. 352 с.

4. Сколник М. Введение в технику радиолокационных систем. М: Мир, 1965, 748 с.

5. Чижов А.А., Лебедев А.С., Курочкин А.Н. Экспериментальные исследования эффективности проекционного метода сверхрэлеевского разрешения // Вопросы радиоэлектроники, серия РЛТ, выпуск 1, 2011, 139-147 сс.

6. Кузьмин С.З. Цифровая радиолокация. Киев: КВiЦ, 2000, 428 с.

7. Вудворд Ф.М. Теория вероятностей и теория информации с применениями в радиолокации. М.: Советское радио, 1955, 128 с.

8. Бурдик B.C. Анализ гидроакустических систем. Ленинград: Судостроение, 1988, 392 с.

Способ измерения дальности цели в ближней радиолокации, в котором принятые в радиолокационной станции колебания дискретизуют в аналого-цифровом преобразователе, затем выделяют огибающую принятого сигнала с большим отношением сигнал-шум, далее определяют временную задержку принятого сигнала с точностью до периода дискретизации, которая определяет дальность до цели, отличающийся тем, что формируют опорный сигнал, смещенный на время, соответствующее полученной временной задержке, после чего вычисляют разность фаз принятого сигнала и опорного, полученное значение пересчитывают в поправку к дальности относительно первоначально измеренного значения дальности до цели.