Оптический способ дистанционного измерения размеров частиц в аэрозольных облаках

Оптический способ дистанционного измерения размеров частиц в аэрозольных облаках

Иллюстрации

Показать все

Реферат

Изобретение относится к измерительной технике, в частности к способам определения размеров частиц в аэрозольных облаках, и может быть использовано в целях охраны окружающей среды и оценки маскировочной обстановки.

Известные оптические способы определения размеров аэрозольных частиц основаны на решении задач поглощения и рассеяния электромагнитного излучения на частицах различных размеров [Шифрин К.С, Раскин В.Ф. Спектральная прозрачность и обратная задача теории рассеяния. Оптика и спектроскопия. 1961, т. 11, №2, с. 268-271]. На этом принципе предложен ряд способов и устройств определения размеров аэрозольных частиц при использовании как белого света, так и монохроматического излучения, например [Патент RU 2098794 С1, 10.12.1997, МПК ⁶ G01N 15/02; Патент RU 2235990 С1, 10.09.2004, МПК ⁷ G01N 15/02; Патент RU 2123176 С1, 10.12.1998, МПК ⁶ G01N 21/25; Патент RU 2239173 С1, 27.10.2004, МПК ⁷ G01N 15/02].

Общим недостатком известных способов является отсутствие дистанционности при определении размеров частиц в аэрозольных облаках. Т.е. из облака отбирают пробу, которую затем помещают в устройство определения размеров аэрозолей, принцип работы которого основан на взаимодействии оптического излучения с аэрозолями.

Отбор проб не всегда технически возможен и экономически обоснован. Результаты анализа получаются не в реальном масштабе времени. Кроме того, при взрывных работах и пылении, создаваемом при движении тяжелой техники, наблюдается быстрое выпадение крупнодисперсных аэрозолей и поэтому оптические характеристики облака быстро изменяются. Т.е. вышеуказанные способы можно использовать, если облако состоит из мелкодисперсных аэрозолей, с длительным временем их существования в воздухе.

Дистанционность достигается за счет измерения оптического излучения, рассеянного аэрозольным облаком. Поскольку размеры аэрозолей, образующихся при взрывах и пылении, не менее единиц микрометров, то для решения поставленной задачи - дистанционного измерения размеров частиц в реальном масштабе времени целесообразно использовать видимую часть оптического диапазона без активной подсветки облака.

Известна зависимость оптической плотности аэрозольного облака от распределения частиц в нем, по концентрациям и размерам [В.Е. Зуев, М.В. Кабанов. Оптика атмосферного аэрозоля, М.: Гидрометеоиздат, 1987].

Основной трудностью, препятствующей реализации предлагаемого способа прототипа, является многопараметричность задачи, т.к. оптическая плотность облака зависит от начальной концентрации аэрозольных частиц, распределения этих частиц по размерам, а также от времени выпадения частиц из облака. Для практической реализации способа на первом этапе необходимо создать математическую модель, устраняющую вышеуказанную неопределенность.

Согласно теории объемного рассеяния Ми для частиц, размер которых много больше длины волны видимого излучения, объемный коэффициент рассеяния определяется выражением

где N₀ - число частиц в единице объема рассеивающего облака, R_cp - усредненный радиус частиц. Объем частицы . Среднее число частиц в облаке обозначим как N. Тогда и предыдущее выражение можно записать следующим образом:

Оптическая плотность облака, зафиксированная на видеоносителе, например, с использованием цифровой видеокамеры

где P_i - повторяемость градаций частиц в их законе распределения по размерам.

Введем понятие нормированной оптической плотности облака Q(t)/Q_max. Здесь Q_max - максимальная оптическая плотность облака в начальный момент времени, когда выпадение частиц из облака еще не происходило. Отношение Q(t)/Q_max уже не зависит от начальной концентрации аэрозолей. Т.е. нормированная оптическая плотность облака зависит только от распределения частиц по размерам и времени и определяется временем осаждения аэрозольных частиц.

На выпадающую частицу действуют две силы: 1) сила тяжести , где ρ - плотность частицы, R - ее радиус; 2) сила сопротивления при движении в вязкой среде. В случае стационарного облака и ламинарного движения сферической частицы эта сила является силой Стокса , где η - коэффициент динамической вязкости воздуха, υ - скорость движения частицы. Тогда движение падающей частицы описывается дифференциальным уравнением

где - характеристический параметр движения частицы.

Решением уравнения (4) является следующее выражение:

Движение частицы происходит с переменным ускорением. Но при b≥4 частицы практически мгновенно достигают скорости равномерного движения υ₀=g/b.

Интегрирование уравнения (5) определяет путь H, проходимый аэрозольной частицей за время t.

Соответственно из уравнения (6) можно определить время t₀ осаждения частиц с радиусом R₀ с высоты Н₀ до момента падения на Землю. Т.е. за время t₀ выпадают частицы с радиусами R≥R₀, и соответственно уменьшается оптическая плотность облака.

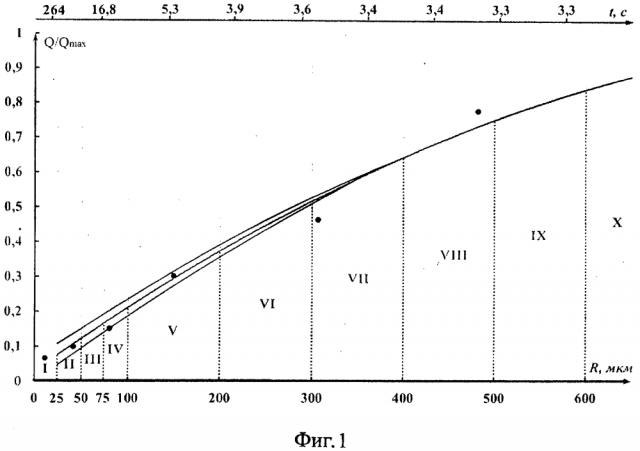
Измеряя среднюю высоту аэрозольного облака [Михеев С.В. Исследование оптико-электронной системы контроля положения объекта методом триангуляции. Дис. канд. тех. наук. 2007. Санкт-Петербургский Государственный университет информационных технологий, механики и оптики. 124 с.], можно вычислить время выпадения частиц различных размеров и плотности. На фиг. 1 представлена номограмма, связывающая время выпадения частиц различных размеров и нормированную оптическую плотность облака, при его средней высоте 50 м. При радиусе частиц R≥300 мкм они падают практически свободно, не зависимо от их плотности. При меньших размерах время выпадения зависит от плотности частиц, что отражено на номограмме в виде двух ветвей, когда плотность изменяются от 1,5·10³ кг/м³ - частицы почвы, до 11·10³ кг/м³ - частицы тяжелых металлов. Средний радиус аэрозольной частицы определяется по попаданию точки пересечения линий времени выпадения и оптической плотности облака в ту или иную градацию.

Техническим результатом изобретения является дистанционное определение закона распределения частиц по размерам в аэрозольных облаках в оптическом диапазоне электромагнитного спектра.

Указанный технический результат достигается тем, что в течение времени существования аэрозольного облака, с использованием цифрового видеорегистратора измеряют оптическую плотность облака, вычисляют нормированную оптическую плотность облака, измеряют среднюю высоту аэрозольного облака, рассчитывают промежутки времени, за которые в выбранных градациях выпадают частицы соответствующих радиусов, и распределение аэрозольных частиц по размерам определяют по попаданию точки пересечения линий времени выпадения частиц и нормированной оптической плотности облака в ту или иную градацию на номограмме.

В качестве примера рассмотрим процесс выпадения частиц гранита с плотностью ρ=2,5·10³ кг/м³ из аэрозольного облака, образовывающегося при буровзрывных работах. Высота облака Н₀=50 м. Грансостав выпавших частиц определялся методом осаждения в жидкости. В таблице приведены усредненные размеры выпавших частиц по девяти градациям, а также их повторяемости Р. Мелкодисперсная взвесь с радиусом R≤3 мкм образовывалась при бурении. Оставшиеся 88% частиц образовались при взрыве. По уравнению (5) определено время осаждения t₀ частиц в воздухе по всем градациям. Для этих же градаций в таблице приведена нормированная оптическая плотность облака Q/Q_max, определенная по результатам цифровой видеосъемки. Для частиц с радиусами меньшими 3 мкм, оптическая плотность облака сравнивалась с фоном неба и не регистрировалась.

На фиг. 1 показаны экспериментальные точки пересечения линии времени выпадения частиц гранита, присутствующих в облаке и его нормированной оптической плотности. Как видно из фиг. 1 - получено хорошее совпадение экспериментально измеренных радиусов частиц, выпавших из облака, и оценок их радиусов по номограмме, что подтверждает достоверность результатов, полученных с использованием предложенного способа.

Таким образом, измеряя высоту и нормированную оптическую плотность облака и вычисляя время выпадения аэрозольных частиц заданных размеров и плотности, можно по номограмме дистанционно определить закон распределения частиц по размерам в аэрозольных облаках.

Оптический способ дистанционного измерения радиусов частиц в аэрозольных облаках, основанный на обработке оптического излучения, рассеянного аэрозолями облака, отличающийся тем, что в течение времени существования аэрозольного облака измеряют оптическую плотность облака, вычисляют нормированную оптическую плотность облака, измеряют среднюю высоту аэрозольного облака, рассчитывают промежутки времени, за которые в выбранных градациях выпадают частицы соответствующих радиусов, и распределение аэрозольных частиц по размерам определяют по попаданию точки пересечения линий времени выпадения частиц и нормированной оптической плотности облака в ту или иную градацию на номограмме.