Способ линейного преобразования (варианты)

Способ линейного преобразования (варианты)

Иллюстрации

Показать все

Реферат

Область техники, к которой относится изобретение

Предлагаемое изобретение относится к области вычислительной техники и криптографии и, в частности, к использованию регистров сдвига для реализации линейного преобразования большой размерности и последующего применения в устройствах криптографической защиты данных.

Уровень техники

Для криптографической защиты данных используются различные способы реализации линейных преобразований.

Так, известен способ, улучающий и программную, и аппаратную реализацию фиксированного линейного преобразования шифра AES, основанный на использовании специфического вида матрицы линейного преобразования. Известный способ относится к криптографической области и также может быть использован для программной или аппаратной реализации в системах защиты информации [1].

Известны также и другие способы линейных преобразований [2-4].

Недостатками известных способов являются невозможность их применения для реализации произвольных линейных преобразований, в том числе больших размерностей, и неэффективное использование ресурсов для ряда вычислительных платформ.

Перспективным для реализации линейного преобразования является использование регистров сдвига с линейной обратной связью (РСЛОС) [5]. Такие регистры, выполняемые программно или аппаратно и способные работать как в прямом, так и в обратном направлении, могут быть реализованы на различных вычислительных платформах (фиг. 1-4).

Опубликовано большое количество научных работ, где предложено осуществление линейных преобразований на основе различных РСЛОС, включая РСЛОС типа Галуа и Фибоначчи.

Но такие линейные преобразования обычно имеют малую размерность. При построении рассеивающего слоя криптографического преобразования, например блочного шифра или хэш-функции, они не позволяют обработать целый блок большой размерности и требуют дополнительного линейного преобразования для повышения уровня защищенности, например, в стандарте AES - это функция ShiftRows(), в блочном шифре LED - функция ShiftCells(), в хэш-функции ГОСТ Р 34.11-2012 - функция перестановки байт. Обычно использование линейных преобразований малой размерности компенсируется увеличением числа раундов криптографического преобразования для достижения высокой стойкости, что ведет к снижению быстродействия.

Наиболее близким по своей технической сущности к заявляемому является способ [2], позволяющий эффективно реализовать РСЛОС, который выполняет линейную операцию и может быть применен для линейного преобразования. Способ основан на использовании разделимых таблиц и предложен для реализации РСЛОС только в двоичном поле.

Этот способ принимается за прототип.

Другой известный способ [3] позволяет реализовать РСЛОС большого размера, требует мало памяти, но работает медленно, а способ [4] работает быстро, но требует очень много памяти.

Недостатком прототипа и перечисленных известных способов является невозможность выбора параметров вычислительной системы для эффективного использования ее ресурсов, что не позволяет сократить количество необходимых тактов работы используемых в системе процессоров для вычисления результата преобразования.

Раскрытие изобретения

Техническим результатом является обеспечение возможности выбора взаимосвязанных характеристик (быстродействие и объем необходимой памяти) для конкретной вычислительной системы при реализации линейного преобразования большой размерности.

Для этого предлагается способ, позволяющий осуществить линейное преобразование исходного сообщения с использованием РСЛОС типа Галуа фиг. 1, 2 или типа Фибоначчи фиг. 3, 4.

При этом, зная разрядность процессора и объем выделенной для реализации способа памяти, можно заранее определить, сколько тактов работы РСЛОС необходимо для вычисления линейного преобразования исходного сообщения.

Вариант предлагаемого способа, предусматривающий построение РСЛОС типа Галуа и линейного преобразования сообщения S, представленного в двоичном виде, заключающийся в том, что

• задают разрядность W процессора вычислительной системы (размер машинного слова), равную целочисленной степени числа 2;

• задают доступный объем памяти вычислительной системы М бит;

• задают размер s сообщения S, причем s кратно W;

• задают значение разрядности n регистра сдвига с линейной обратной связью (РСЛОС) по схеме Галуа (фиг. 1, 2), причем выполняется соотношение

,

где N∈0, 1, 2, …,

• формируют РСЛОС по схеме Галуа со следующими параметрами:

внутренний примитивный полином

,

a_i∈GF(2)

внешний полином

,

где - количество ячеек РСЛОС,

причем h_i∈GF(2ⁿ),

исходное состояние ячеек РСЛОС q_i образует вектор данных

X=(q_m-1, q_m-2, …, q₂, q₁, q₀),

причем q_i∈GF(2ⁿ), 0≤i≤m-1

выходное состояние ячеек РСЛОС за один такт работы образует вектор

,

причем , 0≤i≤m-1,

где , для 1≤i≤m-1,

• определяют все делители числа m в виде значений р₀, р₁, …, p_d, причем p₀<p₁< … p_d;

• выбирают максимально возможный делитель р из соотношения

;

• модифицируют РСЛОС, выполняя следующие действия:

○ вычисляют R матриц H_r, причем r=(R-1), …, 0. размерностью n×k строк, каждая из которых имеет длину n×k бит, выполняя следующие действия:

▪ вычисляют

k=p,

▪ вычисляют

,

где R - количество матриц Н;

▪ вычисляют

j=m-k;

▪ вычисляют

t=0;

▪ (А1) если не выполняется соотношение

j≤m-1,

то переходят к выполнению этапа A3;

▪ вычисляют

l=0,

▪ (А2) если не выполняется соотношение

l<n,

то вычисляют

j=j+1,

t=t+1,

переходят к выполнению этапа А1;

▪ устанавливают исходное состояние РСЛОС

X=(q_m-1, …, q₁, q₀),

, 0≤i≤m-1,

где q_i∈GF(2ⁿ),

▪ вычисляют после k тактов работы для каждого исходного состояния новое состояние РСЛОС

,

где , 0≤i≤m-1,

▪ вычисляют t-e значения для всех матриц H_i, i=r-1…0 путем конкатенации k значений ячеек q′

,

причем 0≤r≤R-1,

▪ вычисляют

l=l+1,

переходят к выполнению этапа А2;

• (A3) записывают в ячейки модифицированного РСЛОС блоки s исходного сообщения S, причем исходное состояние ячеек модифицированного РСЛОС q_i образует вектор

X′=(Q_R-1, …, Q₁, Q₀),

где Q_r - это содержимое ячеек ,

причем 0≤r≤R-1

• осуществляют R тактов работы модифицированного РСЛОС, выполняя на каждом такте следующие действия:

▪ вычисляют выходное состояние ячеек модифицированного РСЛОС за один такт работы, образующие вектор

,

каждое значение которого вычисляется по формуле

для каждого i=R-1, …, 1,

причем

,

где ,

где z_R-1,j - значение j-го бита вектора Q_R-1,

причем r=R-1, …, 1, 0,

j=0, 1, …, W-1,

z_R-1,j∈GF(2);

• получают после R тактов работы РСЛОС линейное преобразование блоков s сообщения S;

• считывают из ячеек модифицированного РСЛОС блоки линейно преобразованного сообщения s;

• объединяют блоки и получают линейно преобразованное сообщение S.

Вариант предлагаемого способа, предусматривающий построение РСЛОС типа Фибоначчи и линейного преобразования сообщения S, представленного в двоичном виде, заключающийся в том, что

• задают разрядность W процессора вычислительной системы (размер машинного слова), равную целочисленной степени числа 2;

• задают доступный объем памяти вычислительной системы М бит;

• задают размер s сообщения S, причем s кратно W;

• задают значение разрядности n регистра сдвига с линейной обратной связью (РСЛОС) по схеме Фибоначчи (фиг. 3, 4), причем выполняется соотношение

,

где N∈0, 1, 2, …,

• формируют РСЛОС по схеме Фибоначчи со следующими параметрами:

внутренний примитивный полином

,

a_i∈GF(2)

внешний полином

,

где - количество ячеек РСЛОС,

причем h_i∈GF(2ⁿ)

исходное состояние ячеек РСЛОС q_i образует вектор

X=(q_m-1, q_m-2, …, q₂, q₁, q₀),

причем q_i∈GF(2ⁿ), 0≤i≤m-1

выходное состояние ячеек РСЛОС за один такт работы образует вектор

,

причем , 0≤i≤m-1,

где ,

для каждого i=0, …, m-2

• определяют все делители числа m в виде значений р₀, р₁, …, p_d, причем р₀<р₁< … p_d;

• выбирают максимально возможный делитель р из соотношения

;

• модифицируют РСЛОС, выполняя следующие действия:

○ вычисляют R матриц H_r, причем r=(R-1), …, 0, размерностью n×k строк, каждая из которых имеет длину n×k бит, выполняя следующие действия:

- вычисляют

k=р,

▪ вычисляют

,

где R - количество матриц H_r;

▪ вычисляют

r=0;

▪ (А5) если не выполняется соотношение

r<R,

то переходят к выполнению этапа А7;

▪ вычисляют

j=0,

▪ (А6) если не выполняется соотношение

j<k,

то вычисляют

r=r+1,

переходят к выполнению этапа А5;

▪ вычисляют

l=0,

▪ если не выполняется соотношение

l<n,

то вычисляют

j=j+1,

переходят к выполнению этапа А6;

▪ устанавливают исходное состояние РСЛОС

X=(q_m-1, q_m-2, …, q₁, q₀),

, 0≤i≤m-1

где q_i∈GF(2ⁿ);

▪ вычисляют после k тактов работы для каждого исходного состояния новое состояние РСЛОС

,

где , 0≤i≤m-1;

▪ вычисляют (jk+l)-е значение для матрицы H_r путем конкатенации k значений ячеек , , …,

,

причем 0≤r≤R-1;

▪ вычисляют

l=l+1,

переходят к выполнению этапа А6;

• (А7) записывают в ячейки модифицированного РСЛОС блоки s исходного сообщения S, причем исходное состояние ячеек модифицированного РСЛОС q_i образует вектор

X′=(Q_R-1, …, Q₁, Q₀),

где ,

причем 0≤r≤R-1;

• осуществляют R тактов работы модифицированного РСЛОС, выполняя на каждом такте следующие действия:

▪ вычисляют выходное состояние ячеек модифицированного РСЛОС за один такт работы, образующие вектор

,

каждое значение которого вычисляется по формуле

для каждого i=0, …, R-2,

и

,

а значение вычисляется по соотношению

,

где ,

где z_r,j - значение j-го бита вектора Q_r,

причем r=R-1, …, 1, 0,

j=0, 1, …, W-1,

z_r,j∈GF(2);

• получают после R тактов работы РСЛОС линейное преобразование блоков s сообщения S;

• считывают из ячеек модифицированного РСЛОС блоки s линейно преобразованного сообщения S;

• объединяют блоки и получают линейно преобразованное сообщение S.

Для реализации предложенного способа с использованием РСЛОС типа Галуа модифицируют РСЛОС.

Основное отличие модифицированного РСЛОС Галуа - способ вычисления значения функции обратной связи. В модифицированных РСЛОС Галуа значения функции обратной связи регистра вычисляются по таблицам, в зависимости от значений бит старшей ячейки регистра.

Исходное линейное преобразование . Преобразование L задается на основе РСЛОС Галуа над композиционным полем GF((2ⁿ)^m), где s=m×n, с помощью внутреннего примитивного полинома

,

где a_i∈GF(2),

и внешнего неприводимого полинома

,

где h_i∈GF(2ⁿ) и h₀=1.

Исходное состояние ячеек РСЛОС Галуа q_i образует вектор данных

X=(q_m-1, q_m-2, …, q₂, q₁, q₀),

где q_i∈GF(2ⁿ), 0≤i≤m-1.

Элементы композиционного поля GF((2ⁿ)^m) также вычисляются с помощью следующего регистра сдвига с линейной обратной связи типа Галуа (далее РСЛОС) на основе полиномов f(x) и h(y) [4].

Под линейным преобразованием L исходного вектора данных X=(q_m-1, q_m-2, …, q₂, q₁, q₀) будем понимать результат m тактов работы РСЛОС.

Выходное состояние ячеек РСЛОС Галуа за один такт работы образует вектор

,

где , 0≤i≤m-1,

и каждое значение вычисляется по формуле

для каждого i=m-1, …, 1 и .

Операции сложения и умножения двух n-разрядных чисел в РСЛОС Галуа осуществляются в поле GF(2ⁿ). Линейное преобразование исходного вектора данных осуществляется за m тактов работы РСЛОС типа Галуа.

Итогом преобразования является новое состояние регистра на m-ом такте. А обратное линейное преобразование L^-l осуществляется за m тактов работы РСЛОС в обратном направлении.

Пусть р₀, р₁, …, p_d, - все делители числа m, причем р₀<р_х< … p_d. Обозначаются значения k=p_i, и W=nk, где W - разрядность процессора, на котором реализуется исходное линейное преобразование, p_i выбирается исходя из размера доступной памяти М. При этом общая схема модифицированного РСЛОС Галуа имеет вид, показанный на фиг. 5.

Пусть исходное состояние ячеек модифицированного РСЛОС Галуа образует вектор

X′=(Q_R-1, …, Q₁, Q₀),

где Q_r равно содержимому ячеек ,

причем 0≤r≤R-1.

Выходное состояние ячеек модифицированного РСЛОС Галуа за один такт работы образует вектор , и каждое значение для каждого r=R-1, …, 1 вычисляется по формуле

причем

,

а функция определяется в виде

,

где r=R-1, …, 1, 0,

z_R-1,j∈GF(2),

j=0, 1, …, W-1 - биты ячейки Q_R-1 модифицированного РСЛОС Галуа.

Если состояние на m-ом такте есть результат линейного преобразования L по схеме РСЛОС Галуа (фиг. 1), то такое же состояние будет получено на R-ом такте работы модифицированного РСЛОС Галуа (фиг. 5). Причем R тактов работы модифицированного РСЛОС требуют

операций проверки "true - false" для всех бит ячейки Q_R-1. Количество сложений по модулю два W-разрядных чисел для каждого вычисления значения по каждой таблице равно W - 1. Следовательно, каждый такт работы модифицированного РСЛОС Галуа требует следующего количества сложений

В итоге необходимое количество сложений по модулю два W-разрядных чисел для R тактов работы модифицированного РСЛОС Галуа равно

Объем необходимой памяти равен

для сохранения R таблиц H_r, r=15, …, 0.

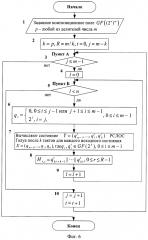
Для правильного функционирования схемы фиг. 5 по правилу схемы фиг. 1 (получения одинакового выхода при одинаковых входных данных) необходимо определить R таблиц H_r, r=(R-1), …, 0. Блок-схема процесса их вычисления представлена на фиг. 6.

Последовательность вычисления R таблиц H_r, r=(R-1), …, 0 базируется на принципе суперпозиции линейных преобразований. Входные данные алгоритма - линейное преобразование над заданным композиционным полем GF((2ⁿ)^m), и р - любой из делителей числа m. А выходные - R необходимых таблиц H_r, r=(R-1), …, 0.

Рассмотрим каждый шаг алгоритма (фиг. 6).

Шаг 1 [Блок 2]: Присваивают значения k=р, , j=m-k и t=0;

Шаг 2 [Пункт А - блок 3]: проверяют условие

j≤m-1

• если условие выполняется, то присваивают l=0 (блок 4) и переходят к шагу 3 [Пункту Б];

• если условие не выполняются, то завершают процесс;

Шаг 3 [Пункт Б - блок 5] проверяют условие

l<n

• если условие выполняется, то

○ определяют исходное состояние РСЛОС Галуа (блок 6):

, 0≤i≤m-1,

○ вычисляют новое состояние РСЛОС Галуа после k тактов работы для каждого исходного состояния X=(q_m-1, …, q₁, q₀), где , 0≤i≤m-1 (блок 7),

○ вычисляют t-е значения для всех таблиц Н путем конкатенации k значений ячеек q′ (блок 8):

, 0≤r≤R-1,

○ увеличивают значение l=l+1 (блок 9), и переходят к шагу 3 [Пункту Б];

• если условие не выполняются, то увеличивают значения j=j+1, t=t+1 (блок 10), и переходят к шагу 2 [Пункту А].

Порядок вычисления необходимых таблиц для обратного линейного преобразования L^-1 выполняется аналогичным образом. Но при этом полученный модифицированный РСЛОС типа Галуа будет работать в противоположном направлении с проверкой на "true - false" для всех бит ячейки Q₀ вместо Q_R-1.

Если линейное преобразование задается на основе РСЛОС Фибоначчи над композиционным полем GF((2ⁿ)^m), где s=m×n, с помощью внутреннего примитивного полинома

,

где a_i∈GF(2),

и внешнего неприводимого полинома

,

где h_i∈GF(2ⁿ) и h₀=1,

то можно его реализовать по схеме модифицированного РСЛОС Фибоначчи.

Исходное состояние ячеек РСЛОС Фибоначчи q_i образует вектор данных

X=(q_m-1, q_m-2, …, q₂, q₁, q₀),

где q_i∈GF(2ⁿ), 0≤i≤m-1

Выходное состояние ячеек РСЛОС Фибоначчи за один такт работы образует вектор

,

где , 0≤i≤m-1

и каждое значение вычисляется по формуле

для каждого i=0, …, m-2 и

.

Операции сложения и умножения двух n-разрядных чисел в РСЛОС Фибоначчи осуществляются в поле GF(2ⁿ). Линейное преобразование исходного вектора данных - m тактов работы РСЛОС Фибоначчи (фиг. 3). Итогом преобразования является новое состояние регистра на m-ом такте. А обратное линейное преобразование L^-1 достигается через m тактов работы РСЛОС Фибоначчи в обратном направлении (фиг. 4).

В этом случае общая схема модифицированного РСЛОС Фибоначчи имеет вид, представленный на фиг. 7.

Пусть исходное состояние ячеек модифицированного РСЛОС Фибоначчи образует вектор

X′=(Q_R-1, …, Q₁, Q₀),

где , 0≤r≤R-1.

Выходное состояние ячеек за один такт работы образует вектор

,

и каждое значение вычисляется по формуле для каждого r=0, …, R-2 и

,

где ,

r=R-1, …, 1, 0

z_r,j∈GF(2),

j=0, 1, …, W-1 - биты ячейки модифицированного РСЛОС Фибоначчи.

Если состояние на m-ом такте есть результат линейного отображения L по схеме РСЛОС Фибоначчи на фиг. 3, то состояние на R-ом такте соответствует его результату по схеме модифицированного РСЛОС Фибоначчи на фиг. 7. Причем R тактов его работы требуют

операций проверки "true - false". Количество сложений по модулю два поразрядных чисел для вычисления каждого значения по каждой таблице равно W-1. Следовательно, каждый такт работы модифицированного РСЛОС Фибоначчи требует

операций сложения по модулю два W-разрядных чисел. В итоге необходимое количество сложений по модулю два W-разрядных чисел для R тактов работы регистра равно

Объем необходимой памяти равен

для сохранения R таблиц H_r, r=15, …, 0.

Для корректной работы модифицированной схемы необходимо определить R таблиц H_r, r=(R-1), …, 0. Блок-схема процесса их вычисления представлена на фиг. 8.

Алгоритм вычисления R таблиц H_r, r=(R-1), …, 0 также базируется на принципе суперпозиции линейных преобразований. Входные данные алгоритма - линейное преобразование над заданным композиционным полем GF((2ⁿ)^m), построенное по схеме РСЛОС Фибоначчи, и р - любой из делителей числа m. А выходные - R необходимых таблиц H_r, r=(R-1), …, 0.

Рассмотрим каждый шаг алгоритма.

Шаг 1 [Блок 2]: Присваивают значения k=р, и r=0;

Шаг 2 [Пункт А - блок 3]: проверяют условие

r<R

• если условие выполняется, то присваивают j=0 (блок 4) и переходят к шагу 3 [Пункту Б];

• если условие не выполняется, то завершают процесс; Шаг 3 [Пункт Б - блок 5] проверяют условие

j<k,

• если условие выполняется, то присваивают l=0 (блок 6) и переходят к шагу 4 [Пункту В];

• если условие не выполняется, то увеличивают значение r=r+1 (блок 12), и переходят к шагу 2 [Пункту А];

Шаг 4 [Пункт В - блок 7] проверяют условие

l<n,

• если условие выполняется, то

○ определяют исходное состояние РСЛОС Фибоначчи (блок 8):

, 0≤i≤m-1,

○ вычисляют новое состояние РСЛОС Фибоначчи после k тактов работы для каждого исходного состояния X=(q_m-1, …, q₁, q₀), где , 0≤i≤m-1 (блок 9),

○ вычисляют (jk+l)-е значение для таблицы H_r путем конкатенации k значений ячеек , , …, (блок 10)

○ увеличивают значение l=l+1 (блок 10) и переходят к шагу 4 [Пункту В];

○ если условие не выполняется, то увеличивают значение j=j+1 (блок 11), и переходят к шагу 3 [Пункту Б].

Порядок вычисления необходимых таблиц для обратного линейного отображения L^-l выполняется аналогичным образом. Но при этом необходимо использовать схему РСЛОС Фибоначчи (фиг. 4) для вычисления его состояния (блок 9, фиг. 8). Полученный модифицированный РСЛОС сдвигается в противоположном направлении.

Краткое описание чертежей

На фиг. 1 показана схема работы линейного регистра сдвига с линейной обратной связью типа Галуа в прямом направлении.

На фиг. 2 показана схема работы линейного регистра сдвига с линейной обратной связью типа Галуа в обратном направлении.

На фиг. 3 показана схема работы линейного регистра сдвига с линейной обратной связью типа Фибоначчи в прямом направлении.

На фиг. 4 показана схема работы линейного регистра сдвига с линейной обратной связью типа Фибоначчи в обратном направлении.

На фиг. 5 показана схема работы модифицированного линейного регистра сдвига с линейной обратной связью типа Галуа.

На фиг. 6 показана блок-схема алгоритма вычисления таблиц функции обратной связи модифицированного линейного регистра сдвига с линейной обратной связью типа Галуа.

На фиг. 7 показана схема работы модифицированного линейного регистра сдвига с линейной обратной связью типа Фибоначчи.

На фиг. 8 показана блок-схема алгоритма вычисления таблиц функции обратной связи модифицированного линейного регистра сдвига с линейной обратной связью типа Фибоначчи.

На фиг. 9 показана схема линейного регистра сдвига с линейной обратной связью типа Галуа для прямого линейного преобразования для примера реализации способа.

На фиг. 10 показана схема линейного регистра сдвига с линейной обратной связью типа Галуа для обратного линейного преобразования для примера реализации способа.

На фиг. 11 показана схема работы модифицированного линейного регистра сдвига с линейной обратной связью типа Галуа для прямого линейного преобразования для примера реализации способа.

На фиг. 12 показана схема работы модифицированного 16-разрядного линейного регистра сдвига с линейной обратной связью типа Галуа для прямого линейного преобразования для примера реализации способа.

На фиг. 13 показана схема работы модифицированного 32-разрядного линейного регистра сдвига с линейной обратной связью типа Галуа для прямого линейного преобразования для примера реализации способа.

На фиг. 14 показана схема работы модифицированного 64-разрядного линейного регистра сдвига с линейной обратной связью типа Галуа для прямого линейного преобразования для примера реализации способа.

Осуществление изобретения

Рассмотрим пример реализации предложенного способа с использованием модифицированного РСЛОС типа Галуа.

Предложенный способ может быть реализован в прикладной программе для вычислительной системы, в качестве которой может быть использован компьютер с одним процессором с разрядностью 8 и выше, работающий под управлением операционной системы (например, Microsoft Windows 7).

Прикладная программа, реализующая работу РСЛОС типа Галуа (или типа Фибоначчи), может быть составлена специалистом по программированию (программистом) на основе знания известных принципов и структуры РСЛОС соответствующего типа и действий предложенного способа.

Для удобства при анализе и синтезе, в описании изобретения рассматривается линейное преобразование L с конкретными параметрами, типичными для большого класса криптографических алгоритмов:

• исходное линейное преобразование ;

• композиционное поле GF((2⁸)¹⁶) (m=16, n=8);

• внутренний примитивный полином

для построения поля GF(2⁸);

• внешний неприводимый полином h(y) для построения композиционного поля GF((2⁸)¹⁶)

,

где

h_i∈GF(2⁸)

Схема РСЛОС для прямого преобразования L и РСЛОС для обратного преобразования L^-1 изображены на фиг. 9 и 10 соответственно.

Ранее для линейного преобразования было выявлено полезное в области криптографии свойство: если в ячейки РСЛОС записать любую последовательность символов и «сдвинуть» регистр 16 раз влево в регистре останутся проверочные символы кода с максимальным расстоянием (МДР кода) С(32,16,17) [6]. Минимальное расстояние между любыми кодовыми словами данного кода равно 17. Если взять такой код в качестве линейного преобразования блочного шифра, то оно будет обладать максимальным свойством рассеивания (d=17).

Последовательность работы одного такта РСЛОС:

○ исходное состояние - вектор X=(q₁₅, q₁₄, …, q₂, q₁, q₀), где q_i∈GF(2⁸), 0≤i≤15. Вектор X имеет 16 координат, расположенных слева направо в 16 ячеек РСЛОС, начиная с координаты индексом i=15;

○ в работе РСЛОС Галуа только значение q₁₅ в самой старшей ячейке участвует в выработке значения функции обратной связи;

○ выходное состояние - вектор , где , 0≤i≤15. Значения для каждого i=15, …, 1 вычисляются

,

при этом q₀=h₀·q_l5

Под линейным преобразованием L исходного вектора данных

X=(q₁₅, q₁₄, …, q₂, q₁, q₀)

будем понимать 16 тактов работы РСЛОС.

Итогом преобразования является новое состояние регистра на m-ом такте, которое можно записать следующим образом

,

где , 0≤i≤15 - значения ячеек РСЛОС.

Обратное преобразование L^-1 - 16 тактов работы РСЛОС в обратном направлении.

Обозначим через k какой-нибудь делитель числа m=16 (его выбор определяется имеющейся разрядностью процессора W и допустимым объемом памяти М).

Сущность предлагаемого способа реализации на соответствующей платформе зависит от значения k и основывается на применении принципа суперпозиции при рассмотрении влияния каждого бита текущего состояния РСЛОС на последующее. В соответствии с тем, что для каждого k имеется способ реализации преобразования L на (nk)-разрядном процессоре.

Рассмотрим следующие случаи.

Расчетный случай 1: k=1. В этом случае рассматривается способ реализации преобразования L на 8-разрядных процессорах (n·k=8·1=8). Для данного случая выполняются следующие действия:

• вычисляют количество r необходимых вычисляемых таблиц H_j, j=15, …, 0

• вычисляют 16 таблиц H_j, j=15, …, 0, каждая из них имеет nk=8·1=8 элементов, а элементы представляют собой 8-разрядные числа (элементы поля GF(2⁸)), выполняя следующие действия:

○ вычисляют соответствующее состояние РСЛОС (фиг. 1) после k=1 тактов по каждому исходному состоянию

для всех q₁₅=2^l, l=0, …, 7, т.е. рассматривают влияние каждого бита числа q₁₅ на состояние РСЛОС (фиг. 1) после k=1 тактов, в результате получают nk=8 состояний;

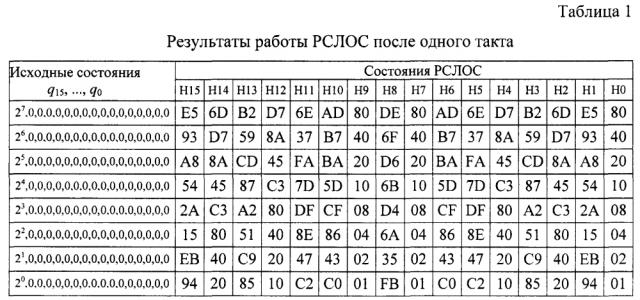
○ составляют массив А из nk=8 полученных состояний таким, что последняя его строка соответствует состоянию при j=m-k=16-1=15 и l=0, предпоследняя его строка соответствует состоянию при j=m-k=16-1=15 и l=1, и т.д. В результате чего массив А имеет nk=8 строк и m=16 столбцов. Первый столбец массива А соответствует значениям ячейки q₁₅, второй - q₁₄ и т.д. (табл. 1);

○ в случае k=1 таблицы H_j, j=15, …, 0 равны каждому столбцу массива А в соответствии с индексами.

• строят расширенную схему РСЛОС (фиг. 5), который имеет r=16 ячеек, значение каждой из которых представляет собой 8-разрядное число;

• обозначают через (Q_l5, Q₁₄, …, Q₂, Q₁, Q₀) состояние расширенного РСЛОС, где Q_i∈GF(2⁸), i=15, 14, …, 0;

• определяют значение f (H_j) функции обратной связи для каждой H_j по формуле

,

где j=15, …, 1, 0,

w_15,u∈GF(2)

u=0, 1, …, 7 - биты ячейки Q₁₅ расширенного РСЛОС.

Это значит, что если u-й бит ячейки Q₁₅ равен единице, то соответствующая строка H_j,u участвует в процессе выработки значения функций обратной связи.

• прямое линейное преобразование L есть r=16 тактов работы расширенного РСЛОС;

• 16 тактов работы расширенного РСЛОС требуют

операций проверки "true - false" для всех битов ячейки Q₁₅ и

операций сложения по модулю два двух n×k-разрядных чисел Q_l и H_l,j, где l=0, 1, …, r-1 и j=0, 1, …, nk.

Объем необходимой памяти равен

для сохранения 16 таблиц H_j, j=15, …, 0.

Порядок реализации обратного линейного преобразования L^-1 на 8-разрядных процессорах выполняется аналогичным образом с использованием РСЛОС (фиг. 2) для вычисления 16 таблиц H_j, j=15, …, 0. За счет симметричности внешнего неприводимого полинома h(y) для рассмотренного линейного преобразования можно использовать те же 16 таблиц H_j, j=15, …, 0 и для реализации прямого преобразования, и для обратного ему.

Расчетный случай 2: k=2. В этом случае рассматривается способ реализации преобразования L на 16-разрядных процессорах. Данный способ включает следующие действия:

• вычисляют количество r необходимых вычисляемых таблиц H_j, j=7, …, 0

• вычисляют r=8 таблиц H_j, j=7, …, 0, каждая из них имеет nk=8·2=16 элементов, а элементы представляют собой 16-разрядные числа, выполняя следующие действия:

○ вычисляют соответствующее состояние РСЛОС (фиг. 1) после k=2 тактов по каждому исходному состоянию

для всех

q_j=2^l, j=14, 15 и l=0, …, 7,

начиная с ячейки на позиции j=m-k=16-2=14, т.е. рассматривают влияние каждого бита числа на состояние РСЛОС (фиг. 1) после k=2 тактов. В результате получают nk=16 состояний;

○ составляют массив А из nk=16 полученных состояний таким, что последняя его строка соответствует состоянию при j=m-k=16-2=14 и l=0, предпоследняя его строка соответствует состоянию при j=m-k=16-2=14 и l=1, и т.д., и первая строка массива А соответствует состоянию при j=m-1=16-1=15 и l=n-1=8-1=7. В результате чего массив А имеет nk=16 строк и m=16 столбцов;

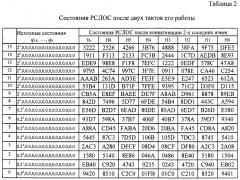
○ формируют r=8 таблиц H_j, j=7, …, 0, начиная со значения j=(r-1)=8-1=7, путем конкатенации k=2 значений в соседних столбцах массива А, начиная с первого его столбца, причем нумеруют таким образом, например, для таблицы H₇, чтобы значение в первой строке первого столбца после конкатенации соответствует H_7,15, а значение в последней строке того же столбца соответствует Н_7,0 (табл. 2).

• строят расширенную схему РСЛОС, причем расширенны