Ик спектроскопический способ определения анизометрии частиц наполнителя в объеме полимерной матрицы

Ик спектроскопический способ определения анизометрии частиц наполнителя в объеме полимерной матрицы

Иллюстрации

Показать все

Реферат

Изобретение относится к области исследования частиц наполнителя в объеме полимерной матрицы с помощью ИК спектроскопии, в частности к методам экспресс-анализа анизометрии полимерных композитов методом Фурье-ИК спектроскопии.

Определение анизометрии частиц наполнителя в полимерных композитах важно для прогнозирования их физических и механических свойств. Равномерным распределением анизометричных частиц наполнителя в полимерной матрице удается добиться существенного улучшения свойств полимерного материала. При этом наполнитель с большей анизометрией формы обладает большим усиливающим действием.

Известен способ определения формы и размера частиц наполнителя в объеме полимерной матрицы с помощью метода малоуглового рентгеновского рассеяния.

Картина малоуглового рассеяния является результатом интерференции когерентно рассеянных на образце лучей. При длинах волн рентгеновского излучения от 0,05 до 0,5 нм метод малоуглового рассеяния позволяет исследовать структуры размерами от единиц до нескольких сотен нанометров. Интерференционная картина рассеяния формируется сложением множества вторичных когерентно рассеянных волн, которые отличаются друг от друга по фазе. Фазовые отличия и амплитуды слагаемых волн зависят от пространственного распределения электронной плотности, т.е. от структуры исследуемого объекта, которая и определяет форму экспериментальной кривой рассеяния I(s), где s - вектор рассеяния. Его модуль определяется выражением

, где

Θ - угол рассеяния; λ - длина волны рентгеновского излучения.

Анализ кривой позволяет определить электронный радиус инерции и максимальный размер частиц в монодисперсных системах и их распределение по размерам - в полидисперсных. Метод определения структурных параметров частиц и их распределения по размерам основан на математической обработке результатов измерений угловой зависимости интенсивности рассеянного образцом рентгеновского излучения.

Недостатками способа являются: сложность математической обработки экспериментальных результатов; интерпретация данных малоуглового рассеяния требует предварительных характеристик исследуемого объекта; детектируемые размеры лежат в узком диапазоне от 1 до 100 нм.

Известен способ измерения размера и формы частиц методом оптической и электронной микроскопии.

Оптическая микроскопия позволяет оценить реальные размеры и форму частиц. Метод позволяет определить степень дисперсии и образование в анализируемой системе агломератов. Приборное обеспечение для оптической микроскопии недорого. Следует заметить, что 1 г материала, состоящий из частиц размером 10 мкм и плотностью 2,5 г/см³, содержит 760×106 частиц. При таком количестве частиц невозможно рассмотреть каждую частицу в отдельности. Случайные и систематические погрешности при использовании этого метода возникают из-за непредставительного пробоотбора, статистики подсчетов и ошибочной идентификации фаз оператором.

Недостатком способа является невозможность использования оптической микроскопии для дисперсного анализа в условиях массового производства.

Использование дорогостоящих электронных микроскопов в сочетании с системами обработки изображения позволяет анализировать состав фаз.

Недостатки способа электронной микроскопии: сложная пробоподготовка, длительность анализа, неприемлемая для использования в условиях производства.

В основу изобретения положена задача разработки ИК спектроскопического экспресс-способа определения анизометрии частиц наполнителя в полимерной матрице.

Технический результат настоящего изобретения заключается в разработке ИК спектроскопического экспресс-способа определения анизометрии частиц наполнителя в объеме полимерной матрицы.

Технический результат настоящего изобретения достигается тем, что для оценки анизометрии частиц наполнителя в объеме полимерной матрицы, при условии выполнения условия , где n_М и n_Н - показатели преломления матрицы и наполнителя соответственно, последовательно регистрируют ИК-спектры пропускания, поворачивая образец во фронтальной и/или поперечной плоскостях, производят математическую обработку измеренного спектра с последовательным получением спектров вычитания и кривой распределения частиц наполнителя по размерам, по изменению размера частиц наполнителя при повороте образца определяется анизометрия частиц наполнителя в полимерной матрице.

Изобретение иллюстрируется Фиг. 1-8 и Таблицей 1.

Фиг. 1. ИК спектры ненаполненной и наполненной углеродными наночастицами полипропиленовой пленки и результат вычитания спектров. 1 - ИК спектр ненаполненной полипропиленовой пленки, 2 - ИК спектр пленки, наполненной углеродными наночастицами, 3 - спектр вычитания, полученный в программе Opus.

Фиг. 2. Спектр вычитания полипропиленовой пленки, наполненной углеродными наночастицами и результат аппроксимации, где 1 - спектр вычитания пленки, наполненной углеродными наночастицами, 2 - результат аппроксимации.

Фиг. 3. Результат преобразования спектра вычитания пленки, наполненной углеродными наночастицами.

Фиг. 4. Кривая распределения углеродных наночастиц по размерам в объеме полипропиленовой матрицы.

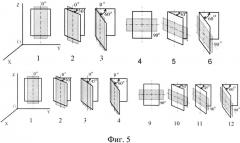
Фиг.5. Схема расположения композитной пленки при регистрации ИК спектров. Направление экструзии совпадает с длинной стороной пленки, а направление ИК излучения перпендикулярно плоскости рисунка.

Фиг. 6. Индикатрисы распределения среднего размера углеродных наночастиц в объеме полипропиленовой матрицы, где а) - неориентированная пленка, с кратностью вытягивания λ=1, б) ориентированная пленка, с кратностью вытягивания λ=8.

Фиг. 7. Индикатрисы распределения среднего размера пор в объеме полимерной матрицы, где а) пористый полистирол, б) пористый полиэтилен.

Сущность изобретения заключается в следующем.

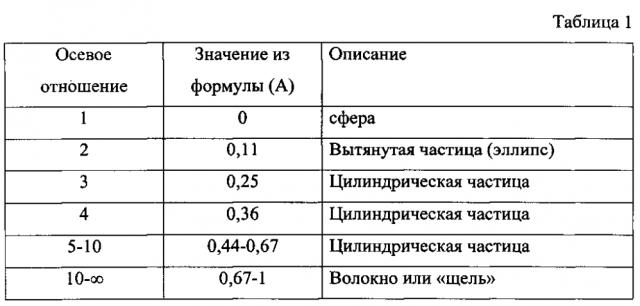
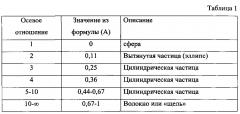
Важной характеристикой рассеивающих частиц является анизометрия их геометрической формы. Обычно рассматриваются частицы наполнителя в сферическом приближении, однако на практике эти частицы часто имеют вытянутую или дискообразную плоскую форму. Фактор анизометрии частиц наполнителя существенно влияет на свойства композита. Обычно принято определять анизометрию рассеивающих частиц с помощью построения индикатрисы рассеяния и анализа ее вида, однако нахождение индикатрис рассеяния или угловых зависимостей рассеянного света является сложной и длительной процедурой.

Согласно геометрическим представлениям, если частица обладает анизометрией формы, то при поворотах такой частицы на различные углы относительно выбранного направления ее размер изменяется.

Для нахождения концентрации и размера рассеивающих частиц, их распределения по размерам используется следующий спектроскопический эффект: в том случае, когда средний диаметр d рассеивающих частиц (поры или частицы наполнителя) совпадают с длиной волны λ падающего излучения, происходит существенное снижение светопропускания, в результате чего в ИК-спектре наблюдается характерный «перегиб» Фиг. 1. Определение среднего размера упруго рассеивающих частиц и их распределения по размерам основано на принципе резонанса: коэффициент рассеяния k_S в случае дифракционного рассеяния d≈λ существенно больше, чем для случая рэлеевского рассеяния (d<<λ, малые рассеивающие частицы) или рассеяния Ми (Mie) (d>>λ, крупные рассеивающие частицы), и действуют законы геометрической оптики.

Рассмотрим алгоритм определения среднего размера частиц наполнителя в полимерной матрице по максимуму кривой распределения частиц по размерам на примере композита - полипропиленовой пленки, наполненной углеродными наночастицами при ее вращении во фронтальной плоскости.

1) Выделяем из ИК-спектра образца полипропиленовой пленки, наполненной углеродными наночастицами компоненту, связанную с рассеянием на частицах наполнителя, путем вычитания из спектра наполненного материала спектра ненаполненного Фиг. 1. Вычитание проводится, например, в программе Opus програмного обеспечения к ИК спектрометру.

2) Аппроксимируем спектр вычитания к функции вида

Фиг. 2.

3) Переводим результат аппроксимации из обратных сантиметров в микрометры по оси X Фиг. 3.

4) Дифференцируем с учетом факта дифракционного рассеяния кривую Фиг. 3 по длине волны и получаем кривую распределения рассеивающих частиц dS/dλ по размерам Фиг. 4.

5) По положению максимума на кривой распределения рассеивающих частиц по размерам Фиг. 4. определяем средний размер рассеивающих частиц.

6) Повторяем п. 1-5 при повороте полипропиленовой пленки, наполненной углеродными наночастицами во фронтальной плоскости.

7) Определяем анизометрию углеродных наночастиц в объеме полипропиленовой матрицы по формуле

,

где min и max - соответственно минимальный и максимальный средний размер рассеивающих частиц при повороте во фронтальной и/или поперечной плоскостях.

Для полимерного композита, представляющего собой неориентированную, с кратностью вытягивания λ=1, полипропиленовую пленку с 1% углеродных волокон из индикатрисы распределения среднего размера углеродных наночастиц в объеме полипропиленовой матрицы Фиг. 6а определяем

Для ориентированной пленки, с кратностью вытягивания λ=8, аналогичного состава из индикатрисы распределения среднего размера углеродных наночастиц в объеме полипропиленовой матрицы Фиг. 6б А=0,013.

Для пористых пленок полистирола и полиэтилена анизометрия частиц наполнителя - воздуха, определенная из индикатрис распределения среднего размера наполнителя Фиг. 7а и 7б, составила соответственно А≈0 и А=0,0004.

Оценить форму частиц наполнителя можно по Таблице 1.

ИК спектроскопический экспресс способ определения анизометрии частиц наполнителя в объеме полимерной матрицы реализован на стандартном оборудовании лаборатории спектроскопии ЦКП ФГБОУ ВО «Тверской государственный университет».

ИК спектроскопический способ определения анизометрии частиц наполнителя в объеме полимерной матрицы, заключающийся в последовательной регистрации ИК спектров пропускания образцов, состоящих из полимерной матрицы и наполнителя, причем |n_М-n_Н|>0, где n_М и n_Н - показатели преломления матрицы и наполнителя соответственно, при повороте образца во фронтальной и/или поперечной плоскостях, преобразовании спектров в кривые распределения частиц наполнителя по размерам, идентификации экстремумов кривых распределения частиц наполнителя по размерам, определении анизометрии частиц наполнителя в полимерной матрице.