Способ измерения теплофизических свойств теплоизоляционных материалов методом плоского импульсного источника теплоты

Способ измерения теплофизических свойств теплоизоляционных материалов методом плоского импульсного источника теплоты

Иллюстрации

Показать все

Реферат

Изобретение относится к области исследования теплофизических характеристик теплоизоляционных материалов.

Известен способ определения комплекса теплофизических свойств твердых материалов [Патент РФ №2125258, кл. G01N 25/18, 1999], включающий воздействие тепловыми импульсами от линейного источника на плоскую поверхность исследуемого и эталонного образцов, измерение избыточных температур в моменты подачи тепловых импульсов в точках, расположенных на фиксированных расстояниях от линии нагрева на поверхности образцов. Измеренные температуры приближают с минимальной погрешностью к рассчитанным температурам, формируемых посредством программного управления параметрами теплофизических характеристик. По идентифицированным параметрам образцов и действительным значениям характеристик эталона определяют искомые характеристики.

Недостатками этого способа являются большая длительность и трудоемкость эксперимента, а также необходимость использования эталонного образца.

Известен способ измерения теплофизических свойств твердых материалов методом плоского мгновенного источника тепла [Пономарев С.В. Теоретические и практические основы теплофизических измерений: монография / под ред. С.В. Пономарева. - М.: ФИЗМАТЛИТ, 2008. - 408 с.], заключающийся в том, что из исследуемого материала изготавливают три пластины, причем одну тонкую толщиной x₀ размещают между двумя массивными, толщина которых в десять-двадцать раз превышает x₀. Между нижней массивной и тонкой пластинами размещают плоский электронагреватель, изготовленный из тонкой нихромовой (манганиновой) проволоки, а датчик температуры, изготовленный из медной проволоки, располагают на расстоянии x=x₀ от нагревателя. Полученную систему предварительно выдерживают при заданной начальной температуре T₀ не менее двух часов. Активная часть эксперимента начинается в тот момент времени, когда на электронагреватель подается короткий электрический импульс. За время действия этого импульса в единице площади плоского нагревателя выделяется количество тепла Q_n. В течение активной стадии эксперимента осуществляют измерение и регистрацию температуры в точке x=x₀, определяют максимальное значение температуры T_max. Активную стадию эксперимента завершают при τ>τ_max, где τ_max - момент времени, соответствующий достижению максимального значения температуры T_max. По полученным данным (x₀, Q_n, T_max, τ_max) вычисляют искомые теплофизические свойства исследуемого материала.

Недостатком данного способа является то, что значение момента времени τ=τ_max по экспериментальным данным определяется с высокой относительной погрешностью, зачастую достигающей величины (15…20)%.

Наиболее близким техническим решением является способ измерения теплофизических свойств твердых материалов методом плоского мгновенного источника тепла [Патент РФ №2534429, кл. G01N 25/18, 2014], заключающийся в том, что образец исследуемого материала изготавливают в виде трех пластин, причем тонкую пластину толщиной x₀ размещают между двумя массивными, толщина которых в десять-двадцать раз превышает x₀. В плоскости x=0 между нижней массивной и тонкой пластинами размещают плоский электронагреватель, изготовленный из пермаллоевой фольги, а термоэлектрический преобразователь располагают в другой плоскости на расстоянии x=x₀ от нагревателя между верхней массивной и тонкой пластинами. Полученную систему предварительно выдерживают при заданной начальной температуре T₀, затем на электронагреватель подают короткий электрический импульс. В течение активной стадии эксперимента осуществляют измерение и регистрацию температуры в точке x=x₀ с постоянным шагом во времени, определяют максимальное значение температуры T_max. После достижения максимального значения температуры T_max активную стадию эксперимента заканчивают, когда разность температур (T_i-T₀) становится меньше величины α(T_max-T₀). Затем рассчитывают значение температуры T′=β(T_max-T₀)+T₀, соответствующее заданному значению параметра β, определяют четыре ближайших к T′ значения T_j-1<T_j, T_j≤T′, T_j+1>T′, T_j+2>T_j+1, вычисляют параметры b₀, b₁ зависимости T=b₀+b₁τ методом наименьших квадратов по четырем парам значений (τ_j-1, T_j-1), (τ_j, T_j), (τ_j+1, T_j+1), (τ_j+2, T_j+2), определяют момент времени τ′ как корень уравнения T′=b₀+b₁τ, а искомые теплофизические свойства рассчитывают по формулам:

;

;

λ=acρ,

где a - температуропроводность исследуемого материала; cρ - объемная теплоемкость исследуемого материала; λ - теплопроводность исследуемого материала; Q_n - количество тепла, мгновенно выделившееся в единице площади плоского нагревателя в момент начала активной стадии эксперимента; z′ - больший корень уравнения ; значение параметра α выбирают из диапазона 0,95…0,98; значение параметра β выбирают из диапазона 0,3…0,6, причем оптимальным является значение β_опт=0,498.

Недостатком данного способа является то, что в математической модели температурного поля внутренний источник теплоты задается в виде плоского мгновенного импульса, хотя в действительности теплота подводится к нагревателю в течение промежутка времени 0<τ<τ_u, где τ_u - длительность реального (не мгновенного) теплового импульса, подводимого к нагревателю. До настоящего времени не рассматривались вопросы о выборе оптимального значения длительности τ_u теплового импульса и рационального конструкционного размера x₀ тонкой средней пластины образца исследуемого материала.

Техническая задача изобретения - повышение точности измерения теплофизических свойств теплоизоляционных материалов за счет выбора оптимальных режимных параметров теплофизического эксперимента и рационального конструкционного размера измерительного устройства.

Техническая задача достигается тем, что в способе измерения теплофизических свойств теплоизоляционных материалов методом плоского импульсного источника теплоты, заключающемся в том, что образец исследуемого материала изготавливают в виде трех пластин, причем тонкую среднюю пластину толщиной x₀ размещают между двумя массивными, толщина которых в десять-двадцать раз превышает x₀, в плоскости x=0 между нижней массивной и тонкой средней пластинами размещают плоский электронагреватель, а термоэлектрический преобразователь располагают в другой плоскости на расстоянии x=x₀ от нагревателя между верхней массивной и тонкой средней пластинами, полученную систему предварительно выдерживают при заданной начальной температуре T₀, затем на электронагреватель подают электрический импульс, в течение активной стадии эксперимента осуществляют измерение и регистрацию температуры в точке x=x₀ с постоянным шагом во времени, определяют максимальное значение температуры T_max, после достижения максимального значения температуры T_max активную стадию эксперимента заканчивают, когда разность температур (T_i-T₀) становится меньше величины α(T_max-T₀) при 0,95≤α≤0,98, рассчитывают значение температуры T′=γ(T_max-T₀)+T₀, соответствующее заданному значению параметра γ, определяют четыре ближайших к T′ значения T_j-1<T_j, T_j≤T′, T_j+1>T′, T_j+2>T_j+1, вычисляют параметры b₀, b₁ зависимости T=b₀+b₁τ методом наименьших квадратов по четырем парам значений (τ_j-1, T_j-1), (τ_j, T_j), (τ_j+1, T_j+1), (τ_j+2, T_j+2), определяют момент времени τ′ как корень уравнения T′=b₀+b₁τ, согласно изобретению на электронагреватель подают тепловой импульс, длительность которого находится в диапазоне 18≤τ_u≤24 сек, определяют ориентировочные значения коэффициентов температуропроводности a _op и теплопроводности λ_op исследуемого материала формулам:

;

,

где ,

q_c - тепловой поток, подводимый к образцу через поверхность x=0 в течение промежутка времени 0<τ≤τ_u; U(τ′) - безразмерная функция, определяемая при заданном ориентировочном значении параметра γ_op=0,5 из уравнения

,

после чего из зависимости

находят и значение толщины , а из зависимости

определяют значение толщины и оптимальную длительность теплового импульса , толщину средней пластины рассчитывают как , а затем путем проведения серии экспериментов осуществляют измерения и последующую обработку полученных данных при найденных значениях x_опт, γ_опт и и в результате получают значения искомых коэффициентов температуропроводности a и теплопроводности λ исследуемого материала по формулам

,

.

Физическая модель измерительного устройства представляет собой ячейку, в которую помещают образец, состоящий из трех пластин: нижней, средней и верхней. Наиболее высокие требования предъявляются к точности изготовления средней пластины заданной толщины x₀=x_опт, грани которой должны быть выполнены строго параллельно друг другу. Между нижней и средней пластинами размещают малоинерционный плоский нагреватель, а между средней и верхней пластинами устанавливают первичный измерительный преобразователь температуры, например термопару.

Математическая модель температурного поля T(x, τ) в плоском образце (в случае использования импульсного плоского источника теплоты) может быть записана в виде:

где - коэффициент температуропроводности; q(τ, τ_u) - импульсный плоский источник теплоты; q_c - тепловой поток, подводимый к образцу через поверхность x=0 в течение промежутка времени 0<τ≤τ_u; h(τ), h(τ-τ_u) - единичные асимметричные ступенчатые функции, задаваемые соотношениями:

τ_u - длительность теплового импульса q(τ, τ_u).

Используемое в математической модели (1)-(4) соотношение (3) графически проиллюстрировано на фиг. 1.

На основе использования принципа суперпозиции решение краевой задачи (1)-(4) с учетом (5) принимает вид

где

- специальная функция, представляющая собой интеграл от функции ; - функция ошибок Гаусса.

Для времени τ≥τ_u решение (6) с учетом (7) принимает вид

где , - безразмерные функции, зависящие от x, τ, τ_u, a, причем .

График зависимости (8) также приведен на фиг. 1.

Из фиг. 1 видно, что рассчитанное по формуле (8) изменение разности температур [T(x, τ)-T₀] в момент времени τ=τ_max достигает максимальное значение [T_max-T₀]=[T(x, τ_max)-T₀], причем этому моменту времени τ=τ_max соответствует определенное значение безразмерной функции .

Разработанная методика обработки экспериментальных данных основана на том, что в рассмотрение вводится безразмерный параметр

представляющий собой отношение текущего значения разности температур [T(x, τ)-T₀], имеющий место в момент времени τ, к максимальному значению [T_max-T₀]=[T(x, τ_max)-T₀] разности температур в момент времени τ=τ_max.

Из фиг. 1 видно, что каждой величине разности температур γ·[T_max-T₀]=[T(x, τ′)-T₀], то есть каждому значению безразмерного параметра γ, соответствует конкретное значение момента времени τ′ и, следовательно, безразмерной функции .

При численном моделировании процесса измерения на компьютере сначала по формуле (8) вычисляли значение разностей температур T(x, τ)-T₀, а затем методом перебора определяли максимальное значение этой разности температур T_max-T₀, которое аналитически записывается в виде

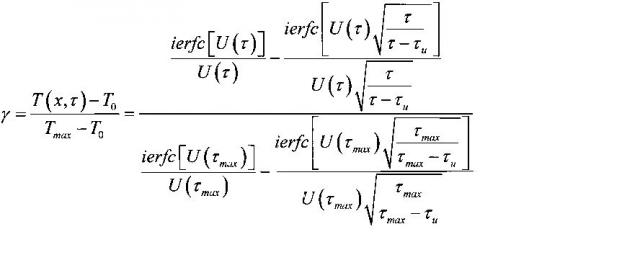
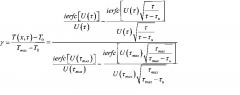
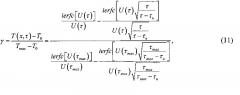
Поделив (8) на (10), получаем уравнение

,

которое легко может быть преобразовано к виду

где принято во внимание, что

.

Если в ходе проведения эксперимента определена величина [T_max-T₀], то (при заранее заданном значении безразмерного параметра γ) путем решения уравнения (11) находят значение безразмерной функции

.

Из последнего соотношения получаем формулу для вычисления искомого значения коэффициента температуропроводности

а с учетом соотношения (8) получаем формулу для вычисления теплопроводности

где .

После получения формул (12), (13) определим, при каких значениях безразмерного параметра γ будут иметь место минимальные погрешности измерения искомых значений a и λ коэффициентов температуропроводности и теплопроводности.

В соответствии с рекомендациями теории погрешностей, после логарифмирования зависимости (12) и последующего определения дифференциала от левой и правой частей, получаем:

Проведя принятую в теории погрешностей:

- замену дифференциалов da≈Δa, dx≈Δx, dτ′≈Δτ′, dU(τ′)≈ΔU(τ′) на абсолютные погрешности Δa, Δx, Δτ′, ΔU(τ′);

- принимая во внимание, что дифференциал константы d4=0;

- заменив знаки "-" знаками "+" в (14), получаем выражение для вычисления так называемой предельной оценки относительной погрешности измерения коэффициента температуропроводности или (δa)_пр=2δx+δτ′+2δU(τ′), где , , , - относительные погрешности определения соответствующих физических величин a, x, τ′, U(τ′).

После перехода от предельной (δa)_пр к среднеквадратичной оценке (δa)_ск погрешности определения коэффициента температуропроводности получаем

Рассмотрим подробнее порядок определения погрешностей, входящих в последнее выражение (15). Принимая во внимание, что значение момента времени τ′ зависит от безразмерного параметра γ, то есть τ′=τ′(γ), получаем

Для определения абсолютной погрешности Δγ выполним (по аналогии с изложенным выше) преобразования формулы (9) и получим

или

где ΔT - абсолютная погрешность измерения разности температур; δ(T_max-T₀) - относительная погрешность измерения максимального значения разности температур (T_max-T₀); Δγ, (δγ)_ск - абсолютная и среднеквадратичная относительная погрешности определения безразмерного параметра γ по экспериментально измеренным значениям разностей температур [T(x, τ′)-T₀] и [T_max-T₀].

Входящая в (15) относительная погрешность δτ′ определения момента времени τ′ также связана с погрешностями измерения разностей температур [T(x, τ′)-T₀]. Из соотношения получаем

где Δτ′, δτ′ - абсолютная и относительная погрешности определения момента времени τ′, соответствующего заданному значению безразмерного параметра γ.

Подставив (16), (17) в формулу (15), получаем соотношение

использованное в дальнейших расчетах с целью выявления оптимального значения безразмерного параметра γ (при измерении коэффициента температуропроводности a).

При выполнении работ (с целью получить соотношение для вычисления среднеквадратичной оценки относительной погрешности (δλ)_ск измерения теплопроводности λ) с учетом того, что при каждом значении длительности τ_u теплового импульса значения: 1) момента времени τ′=τ′(γ); 2) безразмерной функции U(τ′(γ))=U′(γ) зависят от безразмерного параметра γ, формула (13) для вычисления теплопроводности λ была представлена в виде

где F(γ)≡Ф[U(τ′(γ)), U(τ′(γ)-τ_u)].

В результате преобразований, выполненных на основе теории погрешностей по аналогии с изложенными выше действиями с формулами (12)-(18), на основе формулы (19) была получена зависимость для вычисления среднеквадратичной оценки относительных погрешностей (δλ)_ск измерения теплопроводности, имеющая вид:

В процессе расчетов стало очевидно, что относительные среднеквадратичные погрешности (δλ)_ск измерения теплопроводности λ дополнительно зависят от длительности τ_u теплового импульса.

При осуществлении измерений желательно обеспечить выполнение требования о подведении к нагревателю такой величины мощности P, при которой достигаемая в момент времени τ=τ_max в ходе каждого эксперимента максимальная разность температур [T(x, τ_max)-T₀]=[T_max-T₀] на расстоянии x₀ от нагревателя остается примерно одинаковой и находится в определенных пределах, что необходимо по следующим причинам:

- если эта максимальная разность [T_max-T₀] мала, то относительные погрешности измерения значений разностей температур [T(x, τ)-T₀] будут слишком большими, что может привести к росту относительных погрешностей (δa)_ск, (δλ)_ск измерения искомых теплофизических свойств (ТФС);

- если же эта максимальная разность [T_max-T₀] окажется слишком большой, то не будет выполнено предположение о том, что процессы переноса теплоты в образце описываются линейной математической моделью (1)-(4), что опять же приведет к возрастанию результирующих погрешностей (δa)_ск, (δλ)_ск измерения искомых. ТФС из-за нелинейностей, не учитываемых линейной краевой задачей (1)-(4).

Для выполнения этого требования (что [T_max-T₀]≈const) при каждом значении длительности τ_u теплового импульса плоский нагреватель должен обеспечивать создание теплового потока , при котором к единице поверхности внутри образца в каждом эксперименте подводится постоянное количество теплоты

Выше использованы обозначения: - тепловой поток, подводимый нагревателем мощности P и площадью S к нижней стороне средней пластины образца в течение промежутка времени 0≤τ≤τ_u.

Проведенные численные расчеты и экспериментальные исследования показали, что при исследовании образцов теплоизоляционных материалов с толщиной средней пластины 2.5≤x≤5 мм для получения разности температур [T_max-T₀]=3…7°C суммарное количество теплоты Q_n следует поддерживать в пределах .

Рассмотрим подробнее вычисление составляющей погрешности δq_c, входящей в формулу (20). Из изложенного выше следует

т.е. . При этом электрическую мощность P, подведенную к плоскому нагревателю, следует выбирать из соотношения

Для обеспечения требования, что [T(x, τ_max)-T₀]=[T_max-T₀]≈const, при Q_n=const и S=const, величину электрической мощности, подведенную к нагревателю, следует выбирать по формуле (23).

Принимая во внимание, что наиболее точно измеряемой физической величиной в наши дни является время τ, будем считать, что длительность τ_u теплового импульса задается с высокой точностью, а относительная погрешность заданного промежутка времени 0<τ≤τ_u стремится к нулю, т.е. δτ_u≈0%. Тогда для вычисления относительной погрешности δq_c, входящей в формулу (20), воспользуемся соотношением (22).

После логарифмирования (22), определения дифференциалов от левой и правой частей и выполнения других рекомендаций теории погрешностей получаем формулу

в которой величину P(τ_u) вычисляли по формуле (23).

После подстановки (24) в (20) получаем

При вычислениях по формуле (25) принимали ΔP=0,5 Вт, а погрешность измерения площади S нагревателя считали равной δS=0,5%.

С использованием полученных формул (18) и (25) были рассчитаны зависимости среднеквадратичных относительных погрешностей (δa)_ск, (δλ)_ск, при длительности теплового импульса τ_u=10 с. При этом в расчетах были использованы следующие исходные данные: P=55 Вт, , , ΔP=0,25 Вт; Δx=0,1 мм; ΔT=0,05 K, δS=0,5%.

На фиг. 2 показаны зависимости среднеквадратичных относительных погрешностей (δa)_ск и (δλ)_ск от безразмерного параметра γ при различных значениях расстояния x₀ от места действия плоского импульсного источника теплоты до плоскости, в которой размещена термопара, измеряющая разность температур [T(x, τ′)-T₀].

В процессе выполненных исследований выяснилось, что минимальные значения относительных погрешностей (δa)_ск, (δλ)_ск зависят не только от величины безразмерного параметра γ, но и от значения расстояния x₀ от плоскости размещения нагревателя до плоскости установки термопары, измеряющей разность температур [T(x, τ′)-T₀]. В связи с этим были построены линии равных уровней погрешностей на плоскости с координатами γ и x₀ при нескольких значениях длительности теплового импульса τ_u, представленные на фиг. 3 (при τ_u=20 с) и фиг. 4 (при τ_u=5 с).

Представленные на фиг. 3 и фиг. 4 результаты вычислений показывают, что (при использованных в расчетах исходных данных) минимальные значения среднеквадратичных относительных погрешностей (δa)_ск измерения коэффициента температуропроводности a достигаются при значениях безразмерного параметра в диапазоне 0,45<γ≤0,47 и при значениях основного конструкционного размера измерительного устройства в пределах 4,0 мм<x₀≤4,5 мм.

В то же время минимальные значения среднеквадратичных относительных погрешностей (δλ)_ск измерения теплопроводности λ имеют место при 0,95<γ≤1,0 и 2,8 мм<x₀≤3,0 мм.

Таким образом:

1) для достижения минимальных значений погрешности (δa)_ск при измерении коэффициента температуропроводности a следует использовать образец исследуемого материала с толщиной пластины 4,2 мм<x₀≤4,5 мм;

2) для обеспечения минимальных значений погрешности (δλ)_ск при измерении теплопроводности λ требуется использовать образец с толщиной средней пластины 2,8 мм<x₀≤3,0 мм.

Если же необходимо одновременно осуществить измерение коэффициента температуропроводности a и теплопроводности λ в одном эксперименте, то толщину x₀ средней пластины образца из исследуемого материала следует выбирать из диапазона 3,5 мм<x₀≤3,8 мм, что обеспечивает относительные погрешности измерений порядка (δa)_ск≈(6,0…7,1)% и (δλ)_ск≈(5,2…6,4)%.

Для определения значений длительности τ_u теплового импульса, обеспечивающих достижение минимальных значений относительных погрешностей (δa)_ск, (δλ)_ск и среднеарифметических значений погрешностей измерения ТФС a и λ, были выполнены расчеты по формулам (18) и (25), в результате которых можно сделать вывод, что при увеличении длительности τ_u теплового импульса: 1) погрешность (δλ)_ск монотонно возрастает; 2) погрешность (δa)_ск убывает; 3) однако среднеарифметическое значение этих погрешностей принимает минимальные значения при 18<τ_u<24.

Таким образом, при измерении теплофизических свойств исследуемого теплоизоляционного материала следует поступить следующим образом:

- путем проведения предварительных измерений надо определить ориентировочные значения коэффициента температуропроводности a _op и теплопроводности λ_op исследуемого материала;

- осуществить расчеты (при найденных значениях a _op и λ_op) с целью определения (уточнения) оптимальных значений параметра γ_опт и конструкционных размеров и средней пластины, применяемой для измерения коэффициента температуропроводности a и теплопроводности λ;

- принять толщину средней пластины , и рассчитать значение длительности τ_u теплового импульса, обеспечивающего достижение δ_ср=min;

- изготовить образец с одной средней пластиной толщиной ;

- путем проведения серии экспериментов (с изготовленным образцом) осуществить измерения и последующую обработку полученных данных (при найденных значениях γ=γ_опт и ) и в результате получить значения искомых коэффициента температуропроводности a и теплопроводности λ исследуемого материала.

Способ измерения теплофизических свойств теплоизоляционных материалов методом плоского импульсного источника теплоты, заключающийся в том, что образец исследуемого материала изготавливают в виде трех пластин, причем тонкую среднюю пластину толщиной x₀ размещают между двумя массивными, толщина которых в десять-двадцать раз превышает х₀, в плоскости x=0 между нижней массивной и тонкой средней пластинами размещают плоский электронагреватель, а термоэлектрический преобразователь располагают в другой плоскости на расстоянии x=х₀ от нагревателя между верхней массивной и тонкой средней пластинами, полученную систему предварительно выдерживают при заданной начальной температуре T₀, затем на электронагреватель подают электрический импульс, в течение активной стадии эксперимента осуществляют измерение и регистрацию температуры в точке x=х₀ с постоянным шагом во времени, определяют максимальное значение температуры T_max, после достижения максимального значения температуры T_max активную стадию эксперимента заканчивают, когда разность температур (T_i-Т₀) становится меньше величины α(T_max-T₀) при 0,95≤α≤0,98, рассчитывают значение температуры T′=γ(T_max-T₀)+T₀, соответствующее заданному значению параметра γ, определяют четыре ближайших к T′ значения T_j-1<T_j, T_j≤T′, T_j+1>T′, T_j+2>T_j+1, вычисляют параметры b₀, b₁ зависимости T=b₀+b₁τ методом наименьших квадратов по четырем парам значений (τ_j-1, T_j-1), (τ_j, T_j), (τ_j+1, T_j+1), (τ_j+2, T_j+2), определяют момент времени τ′ как корень уравнения T′=b₀+b₁τ, отличающийся тем, что на электронагреватель подают тепловой импульс, длительность которого находится в диапазоне 18≤τ_u≤24 сек, определяют ориентировочные значения коэффициентов температуропроводности a _ор и теплопроводности λ_ор исследуемого материала по формулам: где q_c - тепловой поток, подводимый к образцу через поверхность x=0 в течение промежутка времени 0<τ≤τ_u; U(τ′) - безразмерная функция, определяемая при заданном ориентировочном значении параметра γ_ор=0,5 из уравнения , после чего из зависимости находят и значение толщины , а из зависимости определяют значение толщины и оптимальную длительность теплового импульса , толщину средней пластины рассчитывают как , а затем путем проведения серии экспериментов осуществляют измерения и последующую обработку полученных данных при найденных значениях x_опт, γ_опт и и в результате получают значения искомых коэффициентов температуропроводности а и теплопроводности λ исследуемого материала по формулам