Способ оценки надежности насосной станции

Способ оценки надежности насосной станции

Иллюстрации

Показать все

Реферат

Изобретение относится к области систем водоснабжения и водоотведения и может быть использовано для определения законов распределения случайной величины подачи насосных станций.

Известен метод оценки надежности насосных станций (см. статью одного из авторов данной заявки: Игнатчик С.Ю. Энергосбережение и обеспечение надежности при реконструкции канализационных насосных станций / Водоснабжение и санитарная техника. 2012. №12. С. 37-43). Он позволяет определять технологические и вероятностные показатели надежности для каждого элемента технологической части станции, а также вероятностные и параметрические показатели надежности станции в целом посредством математической модели, описывающей процесс изменения ее состояний в виде Марковского случайного процесса.

Для указанного метода характерна узкая область применения, поскольку он применим только при стационарных потоках отказов и восстановлений оборудования насосных станций, например, на станциях, оборудованных насосными агрегатами, для которых продолжительность устранения внезапных отказов, устраняемых в процессе текущих ремонтов, и постепенных отказов, устраняемых в процессе капитальных ремонтов, существенно не отличаются. Однако на практике встречаются насосные станции, для которых это условие не выполняется, например, станции, оборудованные мощными насосными агрегатами с высоковольтными двигателями. Для них средние продолжительности восстановлений (12000-16000 ч) в процессе капитального ремонта на три порядка больше средних продолжительностей восстановлений в процессе текущего ремонта (60-80 ч). Такой процесс восстановлений не соответствует критериям стационарности. По этой причине, в подобных случаях применение данного метода приведет к снижению точности оценки надежности насосных станций.

Наиболее близким аналогом к заявляемому способу служит Общий логико-вероятностный метод (ОЛВМ), описанный в трудах профессоров Рябинина И.А., Черкесова Г.Н., Можаева А.С.и др. Например, в работе «Сравнительный анализ технологий деревьев отказов и автоматизированного структурно-логического моделирования, используемых для выполнения работ по вероятностному анализу безопасности АЭС и АСУТП на стадии проектирования»: отчет о НИР «Технология-2004» / ФГУП СПб АЭП, ОАО "СПИК СЗМА", ИПУ РАН; ответственные исполнители: Ершов Г.А., Можаев А.С., Викторова B.C. Санкт-Петербург, - 2005 г., стр. 21-22. В соответствии с этим отчетом ОЛВМ включает в себя следующие четыре этапа:

1. Этап структурно-логической постановки задачи, который включает в себя:

- разделение всей рассматриваемой системы на конечное число Н элементов i=1, 2, …, H, каждый из которых представляется в модели надежности простым (бинарным) событием x_i с двумя возможными состояниями x_i={x_i, }, например, работоспособности/отказа, готовности/не готовности, поражения/не поражения и т.д. и заданными вероятностными параметрами p_i(t), или q_i(t)=1-p_i(t);

- определение содержания и логических условий реализации y_i и/или не реализации выходных (интегративных) функций для каждого элемента в системе;

- логически строгое вербальное и графическое (аналитическое) описание множествах X отдельных элементов системы и множества условий Y реализации ими своих системных функций, которые в совокупности G(X,Y) образуют специальную схему функциональной целостности (СФЦ) рассматриваемой системы;

- логически строгое описание и задание с помощью отдельных или групповых выходных (интегративных) функций логических критериев функционирования (ЛКФ) системы реализации основных функций и/или возникновения опасных состояний системы;

2. Этап логического моделирования, на котором с помощью специальных методов преобразования СФЦ и ЛКФ осуществляется построение логической функции работоспособности системы (ФРС) Логическая ФРС позволяет аналитически строго, но в компактной форме, определить все комбинации состояний элементов , в которых (и только в которых) система реализует свою выходную функцию F.

3. Этап вероятностного моделирования, на котором с помощью специальных методов преобразования ФРС осуществляется построение многочлена расчетной вероятностной функции (ВФ) P_F({p_i(t), q_i(t)}, i=1, 2, …, H; t). Многочлен ВФ позволяет аналитически строго определить закон распределения времени безотказной работы системы по реализации выходной функции F, заданной логическим критерием функционирования.

4. Этап выполнения расчетов показателей надежности, которые выполняются на основе ВФ и заданных параметров надежности элементов.

Для указанного метода характерны ограниченные функциональные возможности, поскольку:

- с его помощью нельзя определить технологические показатели надежности в виде распределения не времени безотказной работы, а технологического параметра, например, подачи насосной станции с учетом гидравлических закономерностей совместной работы насосов;

- с его помощью нельзя оценить надежность системы, состоящей из элементов, процесс изменения состояний (работоспособное и отказное) которых происходит под воздействием двух случайных потоков (выход в текущий и капитальный ремонты, продолжительности которых отличаются на порядок и более), т.к. между этими событиями не существует логической связи.

Задачей настоящего изобретения является расширение функциональных возможностей известного метода.

Поставленная задача решается тем, что в известном способе, содержащем этапы, на которых:

а) осуществляют разделение всей рассматриваемой системы на конечное число H элементов i=1, 2, …, H, каждый из которых представляется в модели надежности простым (бинарным) событием с двумя возможными состояниями, например, работоспособности/отказа и вероятностными параметрами;

б) осуществляют вероятностное моделирование с определением закона распределения случайной величины, в соответствии с настоящим изобретением:

1. В качестве i-го элемента насосной станции принимают, по меньшей мере, один насос, по меньшей мере, одного типа в совокупности со всеми другими элементами насосной станции, отказ которых приводит к остановке работы упомянутого насоса.

2. В качестве вероятностных параметров i-го элемента насосной станции принимают интенсивности внезапных отказов λ_i,t, устраняемых в процессе текущих ремонтов, и интенсивности их восстановлений µ_i,t, интенсивности постепенных отказов λ_i,k, устраняемых в процессе капитальных ремонтов, и интенсивности их восстановлений µ_i,k.

3. В качестве случайной величины принимают подачу Q насосной станции.

Кроме того, на этапе а) дополнительно определяют конечное число n состояний насосной станции, j=0, 1, 2, n, и соответствующих им подач Q_j насосной станции, а также допустимую точность σ_доп определения закона распределения случайной величины и назначают продолжительность t имитационного моделирования.

При этом, вероятностное моделирование на этапе б) осуществляют посредством обработки данных результатов имитационного моделирования работы насосной станции, в процессе которого:

параллельно генерируют серию случайных процессов из двух потоков случайных наработок и восстановлений элементов насосной станции, один из которых - с интенсивностью внезапных отказов λ_i,t и интенсивностью восстановлений µ_i,t, второй - с интенсивностью постепенных отказов λ_i,_k и интенсивностью восстановлений µ_i,k;

определяют среднеквадратические отклонения для элементов насосной станции каждого типа

где m₁, m₂ - суммарное количество случайных процессов в серии продолжительностью t случайных наработок между внезапными отказами, устраняемыми в процессе текущих ремонтов, и постепенными отказами, устраняемыми в процессе капитальных ремонтов, t_1,ii, t_2,ii - средние значения по процессам случайных наработок между внезапными отказами, устраняемыми в процессе текущих ремонтов, и постепенными отказами, устраняемыми в процессе капитальных ремонтов,

и, если полученные среднеквадратические отклонения σ₁ и σ₂ превышают допустимую точность σ_доп определения закона распределения случайной величины, то увеличивают продолжительность t имитационного моделирования и повторяют этап б) до тех пор, пока полученные среднеквадратические отклонения σ₁ и σ₂ не уменьшатся до допустимой точности σ_доп,

а, если полученные среднеквадратические отклонения σ₁ и σ₂ не превышают допустимую точность σ_доп определения закона распределения случайной величины, то путем статистического анализа состояний j насосной станции и соответствующих им подач Q_j, полученных в результате имитационного моделирования, получают закон распределения F(q) случайной величины Q, определяющий для каждого значения q вероятность того, что случайная величина подачи Q насосной станции примет значение меньше q, т.е. F(q)=P(Q<q).

Отличительными признаками заявляемого способа являются:

1. Принятие в качестве i-го элемента насосной станции, по меньшей мере, одного насоса, по меньшей мере, одного типа в совокупности со всеми другими элементами насосной станции, отказ которых приводит к остановке работы упомянутого насоса;

2. Принятие в качестве вероятностных параметров i-го элемента насосной станции интенсивностей внезапных отказов λ_i,t, устраняемых в процессе текущих ремонтов, и интенсивностей их восстановлений µ_i,t, интенсивностей постепенных отказов λ_i,k, устраняемых в процессе капитальных ремонтов, и интенсивностей их восстановлений µ_i,k;

3. Принятие в качестве случайной величины подачи Q насосной станции;

4. Дополнительное определение на этапе а) конечного числа n состояний насосной станции, j=0, 1, 2, …, n, и соответствующих им подач Q_j насосной станции;

5. Дополнительное определение на этапе а) допустимой точности σ_доп определения закона распределения случайной величины;

6. Дополнительное назначение на этапе а) продолжительности t имитационного моделирования;

7. Осуществление на этапе б) вероятностного моделирования посредством обработки данных результатов имитационного моделирования работы насосной станции;

8. Параллельное генерирование в процессе имитационного моделирования работы насосной станции в течение продолжительности t серии случайных процессов из двух потоков случайных наработок и восстановлений элементов насосной станции, один из которых с интенсивностью внезапных отказов λ_i,t и интенсивностью восстановлений µ._i,t, второй - с интенсивностью постепенных отказов λ_i,k и интенсивностью восстановлений µ_i,k;

9. Определение среднеквадратического отклонения для элементов насосной станции каждого типа

где m₁, m₂ - суммарное количество случайных процессов в серии продолжительностью t случайных наработок между внезапными отказами, устраняемыми в процессе текущих ремонтов, и постепенными отказами, устраняемыми в процессе капитальных ремонтов, t_1,ii, t_2,ii - средние значения по процессам случайных наработок между внезапными отказами, устраняемыми в процессе текущих ремонтов, и постепенными отказами, устраняемыми в процессе капитальных ремонтов;

10. Увеличение продолжительности t и повторение этапа б) до тех пор, пока полученные среднеквадратические отклонения σ₁ и σ₂ не уменьшатся до допустимой точности σ_доп;

11. Определение закона распределения случайной величины путем статистического анализа состояний j насосной станции и соответствующих им подач Q_j, полученных в результате имитационного моделирования;

12. Получение закона распределения F(q) случайной величины Q, определяющего для каждого значения q вероятность того, что случайная величина подачи Q насосной станции примет значение меньше q, т.е. F(q)=P(Q<q).

По сведениям, имеющимся у авторов, все отличительные признаки не известны. Совместное их применение позволяет расширить функциональные возможности метода, поскольку:

- при его помощи появляется возможность определить технологические показатели надежности в виде распределения случайной величины - технологического параметра, например, подачи насосной станции. Это стало возможно благодаря совместному применению отличительных признаков №1 - 4, 11, 12;

- при его помощи появляется возможность оценить надежность системы, состоящей из элементов, процесс изменения состояний (работоспособное и отказное) которых происходит под воздействием двух случайных потоков (выход в текущий и капитальный ремонты, продолжительность которых отличаются на порядок), между которыми не существует логической связи. Это стало возможно благодаря совместному применению отличительных признаков №1, 2, 5-11.

Краткое описание чертежей.

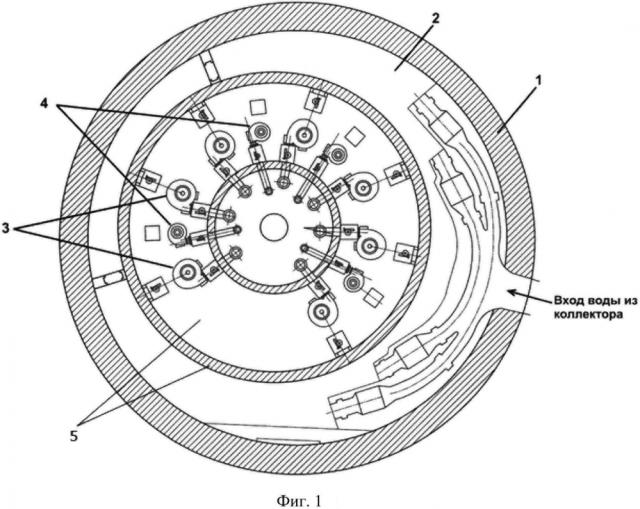
На фиг. 1 представлен вид в плане насосной станции, на фиг. 2 приведен разрез насосной станции по одному из насосов, из которого виден состав i-го элемента насосной станции, на фиг. 3 - таблица с результатами расчета подач Q_j насосной станции во всех состояниях j=0, 1, 2, …, n, на фиг. 4 - схема с примером результатов генерирования двух потоков из серии случайных наработок и восстановлений элементов насосной станции, на фиг. 5 - график с закономерностью изменения среднеквадратического отклонения σ₁ между принятыми в качестве исходных данных и полученными в результате моделирования средними наработками насосов между отказами в зависимости от продолжительности t имитационного моделирования, на фиг. 6 - результаты (в графической форме) определения искомой зависимости распределения случайной величины, на фиг. 7 - функция плотности распределения f(q) случайной величины подач Q насосной станции, полученная путем дифференцирования зависимости распределения случайной величины.

Осуществление изобретения.

На этапе а) осуществляют разделение всей рассматриваемой системы на конечное число H элементов i=1, 2, ..., H, каждый из которых в модели надежности представляется простым (бинарным) событием с двумя возможными состояниями, например, работоспособности/отказа и вероятностными параметрами.

Для иллюстрации особенностей выполнения этого этапа на фиг. 1 представлен вид в плане насосной станции, включающей в себя корпус 1, приемный резервуар 2, и оборудованной двумя типами насосов: высокопроизводительными насосами 3 (7 шт, модель насосов - ФВ 22700/63, расчетная подача - 17,0 тыс. м³/ч) и низкопроизводительными насосами 4 (4 шт, модель насосов - ФВ 9000/63, расчетная подача - 7,5 тыс. м³/ч). Насосы 3 и 4 расположены в машинном отделении 5. В дополнение на фиг. 2 приведен разрез насосной станции по одному из насосов, из которого виден состав i-го элемента насосной станции, включающий в себя, например:

один насос 6;

элементы автоматизированной системы управления (АСУ) 7;

электродвигатель 8;

систему 9 подачи воды на охлаждение электродвигателя; гидравлические домкраты 10;

вал 11;

систему 12 подачи воды на уплотнение вала и подшипника;

всасывающий трубопровод 13;

напорный трубопровод 14;

задвижку 15, установленную на всасывающем трубопроводе 13;

задвижку 16, установленную на напорном трубопроводе 14.

Таким образом, конечное число элементов насосной станции Н=11, каждый из которых может находиться только в двух состояниях: работоспособности и отказа. В каждом из этих элементов при отказе одного из его вышеупомянутых структурных частей, обозначенных позициями 6-16, весь элемент будет находиться в состоянии отказа. Например, при отказе задвижки 15, установленной на всасывающем трубопроводе 13, вода перестанет поступать в насос 6 и весь элемент работать не будет. В состоянии работоспособности i-й элемент будет находиться только тогда, когда работоспособными будут все его части.

В качестве вероятностных параметров i-го элемента насосной станции принимают интенсивности внезапных отказов λ_i,t, устраняемых в процессе текущих ремонтов, и интенсивности их восстановлений µ_i,t, интенсивности постепенных отказов λ_i,k, устраняемых в процессе капитальных ремонтов, и интенсивности их восстановлений µ_i,k. Указанные вероятностные параметры могут быть получены в процессе технического обследования насосной станции или из справочной литературы. Например, по результатам обследования установлено, что:

- первый тип i-го элемента, в состав которого входят высокопроизводительные насосы ФВ 22700/63, имеет следующие вероятностные параметры - интенсивность внезапных отказов λ_i,t=32,6082*10^-4, 1/ч, интенсивности их восстановлений µ_i,t=125,00*10^-4, 1/ч, интенсивности постепенных отказов λ_i,k=0,83333*10^-4, 1/ч, устраняемых в процессе капитальных ремонтов, и интенсивности их восстановлений µ_i,k=0,9375*10^-4, 1/ч;

- второй тип i-го элемента, в состав которого входят низкопроизводительные насосы ФВ 9000/63, имеет следующие вероятностные параметры - интенсивность внезапных отказов λ_i,t=29,2213*10^-4, 1/ч, интенсивности их восстановлений µ_i,t=222,22*10^-4, 1/ч, интенсивности постепенных отказов λ_i,k=0,83333*10^-4, 1/ч, устраняемых в процессе капитальных ремонтов, и интенсивности их восстановлений µ_i,k=0,9375*10^-4, 1/ч.

В качестве случайной величины принимают подачу Q насосной станции.

На этапе а) дополнительно:

- определяют конечное число n состояний насосной станции, j=0, 1, 2, …, n, и соответствующих им подач Q_j насосной станции. Конечное число n состояний зависит от конечного числа Н элементов, а так же количества их типов. Если насосная станция состоит из Н однотипных элементов, то число состояний n=Н+1. При этом, в состоянии 0 все элементы работоспособны. В рассматриваемом примере число состояний элементов с четырьмя низкопроизводительными насосами равно 5, а с семью высокопроизводительными насосами - 8. Тогда общее число состояний насосной станции равно n=5*8=40, т.е. j=0, 1, 2, …, 39. Подача в каждом состоянии определяется суммой подач всех насосов, находящихся в работоспособном состоянии. Например, в состоянии 0, когда все насосы работоспособны, Q₀=7*17,0+4*7,5=149 тыс. м³/ч. Результаты расчета подач во всех остальных состояниях приведены в таблице на фиг. 3. В ней, k_ВП, k_НП - количество отказавших высокопроизводительных и низкопроизводительных насосов;

- дополнительно назначают допустимую точность σ_доп определения закона распределения случайной величины. В соответствии с настоящим изобретением в зависимости от важности насосной станции в системе водоотведения может быть назначена любая точность σ_доп. Как правило, ее принимают равной принятой точности инженерных расчетов, т.е. 5%;

- назначают продолжительность t имитационного моделирования.

Вероятностное моделирование на этапе б) осуществляют посредством обработки данных результатов имитационного моделирования работы насосной станции в течение продолжительности t. Имитационное моделирование известно в данной области техники и доступно для понимания специалистами. Например, его определение содержится в Википедии (https://ru.wikipedia.org): «Имитационное моделирование (ситуационное моделирование) - метод, позволяющий строить модели, описывающие процессы так, как они проходили бы в действительности. Такую модель можно «проиграть» во времени как для одного испытания, так и заданного их множества. При этом результаты будут определяться случайным характером процессов. По этим данным можно получить достаточно устойчивую статистику».

В процессе имитационного моделирования:

1. Параллельно генерируют серию случайных процессов из двух потоков случайных наработок и восстановлений элементов насосной станции, один из которых - с интенсивностью внезапных отказов λ_i,t и интенсивностью восстановлений µ_i,t, второй - с интенсивностью постепенных отказов λ_i,k и интенсивностью восстановлений µ_i,k. Генерирование случайных потоков известно в данной области техники и доступно для понимания специалистами. Например, его определение содержится в Википедии (https://ru.wikipedia.org) в разделе «Генерирование случайных чисел». Генерирование осуществляется с применением «различных генераторов псевдослучайных чисел, для каждого из которых можно задавать конкретное распределение». В настоящее время генератор псевдослучайных чисел имеется в любом компьютере и используется в виде функции в большинстве расчетных программ, например, в Microsoft Excel. Для иллюстрации на фиг. 4 приведен пример такого генерирования одного потока случайных наработок и восстановлений элементов насосной станции одного типа, в состав которого входят низкопроизводительные насосы. В результате получены:

- поток случайных наработок t_1,1, t_1,2, t_1,3, t_1,4, … между внезапными отказами, устраняемыми в процессе текущих ремонтов (позиция 17 на фиг. 4). Они получены с учетом того, что вероятность P(dt) перехода из состояния работоспособности в состояние отказа в течение интервала времени dt равна P(dt)=λ_i,t dt=29,2213*10^-4*dt. При dt=1 ч P(dt)=29,2213*10^-4. В результате получен, например, следующий поток наработок: 350,25; 334,60; 338,39; 365,44 и т.д. часов;

- поток случайных восстановлений τ_1,1, τ_1,2, τ_1,3, τ_1,4, … в процессе текущих ремонтов (позиция 18 на фиг. 4). Они получены с учетом того, что вероятность P(dt) перехода из состояния отказа в состояние работоспособности в течение интервала времени dt равна P(dt)=µ_i,t dt=222,22*10^-4*dt. При dt=1 ч P(dt)=222,22*10^-4. В результате получен, например, следующий поток восстановлений: 76; 81; 79; 81 и т.д. часов;

- поток случайных наработок t_2,1, t_2,2, t_2,3, t_2,4, … между постепенными отказами, устраняемыми в процессе капитальных ремонтов (позиция 19 на фиг. 4). Они получены с учетом того, что вероятность P(dt) перехода из состояния работоспособности в состояние отказа в течение интервала времени dt равна P(dt)=λ_i,k dt=0,83333*10^-4*dt. При dt=1 ч P(dt)=0,83333*10^-4. В результате получен, например, следующий поток наработок: 12050; 12100; 11780; 12001 и т.д. часов;

- поток случайных восстановлений τ_2,1, τ_2,2, τ_2,3, τ_2,4, … в процессе капитальных ремонтов (позиция 20 на фиг. 4). Они получены с учетом того, что вероятность P(dt) перехода из состояния отказа в состояние работоспособности в течение интервала времени dt равна P(dt)=µ_i,k dt=0,9375*10^-4*dt. При dt=1 ч P(dt)=0,9375*10^-4. В результате получен, например, следующий поток восстановлений: 10424,54; 6888,35; 10682,65; 8052,34 и т.д. часов.

2. Определяют среднеквадратические отклонения для элементов каждого типа

и, если полученные среднеквадратические отклонения σ₁ и σ₂ превышают допустимую точность σ_доп определения закона распределения случайной величины, то увеличивают продолжительность t и повторяют этап б) до тех пор, пока полученные среднеквадратические отклонения σ₁ и σ₂ не уменьшатся до допустимой точности σ_доп.

Особенности выполнения этого этапа приведены на фиг. 5, где на примере восстановлений элементов насосной станции одного типа, в состав которого входят высокопроизводительные насосы, показано, как изменяется σ₁ (в %) в зависимости от продолжительности t имитационного моделирования. На этой фигуре позицией 21 обозначены средние наработки насосов между отказами в одной серии, полученные тем же методом имитационного моделирования, позицией 22 - средняя наработка между отказами, принятая в качестве исходных данных и равная 1/λ_i,t=1/32,6082*10⁴=306 часов, позицией 23 - искомое среднеквадратическое отклонение σ₁ между принятыми в качестве исходных данных и полученными в результате моделирования средними наработками насосов между отказами.

Из фиг. 5 так же видно, что если допустимую точность σ_доп определения закона распределения случайной величины принять равной 5%, то придется повторять этап б) до тех пор, пока продолжительность t не достигнет 100 лет.

Далее, путем статистического анализа состояний j насосной станции и соответствующих им подач Q_j, полученных в результате имитационного моделирования, получают закон распределения случайной величины F(q), определяющий для каждого значения q вероятность того, что случайная величина подач Q насосной станции примет значение меньше q, т.е. F(q)=P(Q<q).

На фиг. 6 в графической форме приведены результаты определения искомого закона распределения случайной величины F(q), полученной путем статистического анализа состояний j насосной станции и соответствующих им подач Q_j.

В дополнении, на фиг. 7 приведена функция плотности распределения f(q) подач насосной станции q. Она получена путем дифференцирования функции F(q), т.е. f(q)=F′(q). Расчетная функция плотности распределения f(q) на фиг. 7 обозначена позицией 24. Кроме того, позицией 25 обозначена фактическая функция плотности распределения f(q) подач q (принятой в качестве примера) насосной станции, полученная путем статистической обработки эксплуатационной информации, хранящейся в базах данных автоматизированной системы управления за период 5 лет.

Сопоставление полученных функций плотности распределения (расчетной, обозначенной позицией 24, и фактической, обозначенной позицией 25), доказывает высокую точность прогнозирования подачи насосной станции данным способом. Поскольку пример реализован с применением обычного персонального компьютера, то это доказывает его промышленную применимость.

Способ оценки надежности насосной станции, содержащий этапы, на которых:а) осуществляют разделение всей рассматриваемой системы на конечное число H элементов i=1, 2, …, H, каждый из которых представляется в модели надежности простым событием с двумя возможными состояниями, например, работоспособности/отказа и вероятностными параметрами;б) осуществляют вероятностное моделирование с определением закона распределения случайной величины, отличающийся тем, что в качестве i-го элемента насосной станции принимают, по меньшей мере, один насос, по меньшей мере, одного типа в совокупности со всеми другими элементами насосной станции, отказ которых приводит к остановке работы упомянутого насоса, в качестве вероятностных параметров i-го элемента насосной станции принимают интенсивности внезапных отказов λ_i,t, устраняемых в процессе текущих ремонтов, и интенсивности их восстановлений µ_i,t, интенсивности постепенных отказов λ_i,k, устраняемых в процессе капитальных ремонтов, и интенсивности их восстановлений µ_i,k, в качестве случайной величины принимают подачу Q насосной станции,на этапе а) дополнительно определяют конечное число n состояний насосной станции, j=0, 1, 2, …, n, и соответствующих им подач Q _j насосной станции, а так же допустимую точность σ_доп определения закона распределения случайной величины и назначают продолжительность t имитационного моделирования;вероятностное моделирование на этапе б) осуществляют посредством обработки данных результатов имитационного моделирования работы насосной станции, в процессе которого: параллельно генерируют серию случайных процессов из двух потоков случайных наработок и восстановлений элементов насосной станции, один из которых с интенсивностью внезапных отказов λ_i,t и интенсивностью восстановлений µ_i,t, второй - с интенсивностью постепенных отказов λ_i,k и интенсивностью восстановлений µ_i,k, определяют среднеквадратические отклонения для элементов насосной станции каждого типа , ,где m ₁ , m ₂ - суммарное количество случайных процессов в серии продолжительностью t случайных наработок между внезапными отказами, устраняемыми в процессе текущих ремонтов, и постепенными отказами, устраняемыми в процессе капитальных ремонтов, t_1,ii, t_2,ii - средние значения по процессам случайных наработок между внезапными отказами, устраняемыми в процессе текущих ремонтов, и постепенными отказами, устраняемыми в процессе капитальных ремонтов, и, если полученные среднеквадратические отклонения σ₁ и σ₂ превышают допустимую точность σ_доп определения закона распределения случайной величины, то увеличивают продолжительность t имитационного моделирования и повторяют этап б) до тех пор, пока полученные среднеквадратические отклонения σ₁ и σ₂ не уменьшатся до допустимой точности σ_доп, а если полученные среднеквадратические отклонения σ₁ и σ₂ не превышают допустимую точность σ_доп определения закона распределения случайной величины, то путем статистического анализа состояний j насосной станции и соответствующих им подач Q _j, полученных в результате имитационного моделирования, получают закон распределения F(q) случайной величины Q, определяющий для каждого значения q вероятность того, что случайная величина подачи Q насосной станции примет значение меньше q, т.е. .