Способ создания адаптивного торможения поршня в пневмоцилиндре

Способ создания адаптивного торможения поршня в пневмоцилиндре

Иллюстрации

Показать все

Реферат

Изобретение относится к области автоматизации производственных процессов, в частности в автоматических манипуляторах, а также других автоматических устройствах с пневмоцилиндром, функционирующих в условиях априорной неопределенности о текущем внешнем воздействии на поршень пневмоцилиндра с широким диапазоном возможных его значений и законов изменения, также наличии требования плавного с заданными параметрами торможения поршня пневмоцилиндра в конце его хода.

Известны способы торможения в пневмоцилиндре, основанные на использовании внутренних и внешних тормозных дроссельных устройств [Башта Т.М. Гидропривод и гидропневмоавтоматика. - М: Машиностроение, 1972, стр. 293, 294]. В них тормозное усилие формируется за счет ступенчатого уменьшения проходного сечения отводной магистрали в некоторой точке хода поршня пневмоцилиндра, либо плавного изменения указанного сечения по ходу поршня. Это выполняется с помощью специального выступа на поршне и дополнительной камеры, переключателя в отводной магистрали, тормозного золотника, выпускного дросселя с переменным сечением по ходу поршня и др. При этом тормозное усилие определяется предварительной настройкой выпускного дросселя и момента переключения (закона изменения) сопротивления выпускного дросселя по ходу поршня пневмоцилиндра.

Известно много подобных решений, например патент RU 2447329 С2, 23.06.2010, МПК: F15B 15/22, F16K 31/122.

Наиболее близким к заявленному способу создания адаптивного торможения в пневмоцилиндре является способ демпфирования перемещения поршня в пневмоцилиндре, предполагающий с помощью блока управления и клапанного механизма вначале в зависимости от положения поршня, в т.ч. в начале его движения, повышение давления в выхлопной камере, а через назначенный промежуток времени - стравливание воздуха из нее (прототип) [патент RU 2489608 С1, 20.10.2010, МПК: F15B 11/068, F15B 15/22, F15B 15/28, F16H 61/28].

Основной недостаток указанных способов торможения в пневмоцилиндре (в т.ч. и прототипа) заключается в том, что они рассчитаны на заранее известное значение внешнего воздействия на поршень пневмоцилиндра, закон его изменения при перемещении поршня или достаточно узкую область их возможных вариаций. Поэтому не способны обеспечить требуемого качества торможения в условиях, когда заранее неизвестно значение внешнего воздействия на поршень и характер его изменения при достаточно широкой области их возможных реализаций. В частности, эти способы не учитывают случай, когда внешняя нагрузка изменяется не только по мере перемещения поршня, но и изменяется во времени.

Целью предлагаемого изобретения является устранение недостатка существующих способов торможения поршня в пневмоцилиндре с регулируемым выхлопом в виде обеспечения заданного качества торможения только при заранее известных значениях внешнего воздействия на поршень, закона его изменения при перемещении поршня, или достаточно узкой области их возможных реализаций, а также расширение функциональных возможностей таких устройств.

Поставленная цель достигается использованием адаптивного способа торможения поршня в пневмоцилиндре, который реализуют с помощью управляемого дросселя с изменением проходного сечения, величину которого формируют в зависимости от положения поршня в пневмоцилиндре и давления в выхлопной камере по двухступенчатой схеме адаптивного управления. На первой ступени вычисляют желаемое давление в выхлопной камере на основе оценок первого алгоритма текущей идентификации и параметров основной эталонной модели. На второй ступени формируют величину проходного сечения дросселя на основе желаемого давления, оценки второго алгоритма текущей идентификации и параметра дополнительной эталонной модели. При этом в двухступенчатой схеме адаптивного управления используют рекуррентные алгоритмы текущей идентификации для оценки неизвестных параметров математической модели движения поршня в пневмоцилиндре, а неявные эталонные модели используют для задания требуемых характеристик торможения поршня в пневмоцилиндре и качества управления.

Сущность предлагаемого изобретения поясняется нижеследующим описанием и приведенными фигурами.

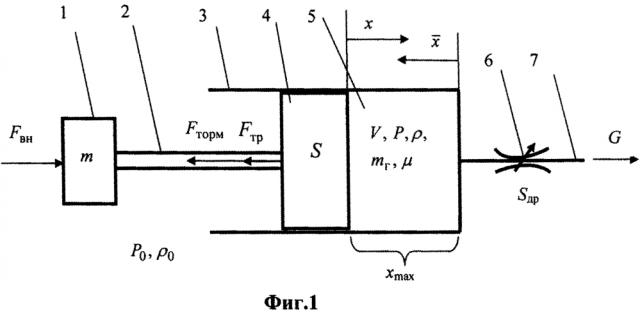
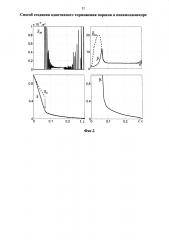
На фиг. 1 показана схема пневматического демпфера с регулируемым выхлопом. На фиг. 2 представлены результаты исследований работы адаптивного демпфера на основе компьютерного имитационного моделирования.

На фиг. 1 представлена схема пневматического демпфера с регулируемым выхлопом с элементами: 1 - присоединенная масса; 2 - шток; 3 - цилиндр; 4 - поршень (поршень, шток и присоединенная масса представляют поршневую группу - единое тело); 5 - выхлопная камера; 6 - регулируемый выхлопной дроссель с изменяемым проходным сечением; 7 - выхлопная магистраль. На фиг. 1 для дальнейших пояснений также введены следующие обозначения: m - масса поршневой группы, является априорно неизвестной величиной; S - площадь поршня; х - перемещение поршневой группы, x∈[0,x_max], где x_max - максимальное значение х или ход поршня; - относительное перемещение поршня в направлении от нулевого объема выхлопной камеры, , ; t, t₀ - текущее время и начальный его момент; V, P, ρ, m_г - объем, давление, плотность и масса газа в выхлопной камере соответственно, примем, что P(t₀)=P₀, V(t₀)=V₀, ρ(t₀)=ρ₀, m_г(t₀)=m_г0, ( - относительное давление); заметим, что ; µ - массовая доля оставшегося газа в камере относительно начального состояния: µ(t)=m_г(t)/m_г0∈[1,0]; G - массовый расход выхлопа (будем считать истечение воздуха в выходном дросселе турбулентным); S_др - площадь проходного сечения выпускного дросселя (считаем круглой трубкой с переменным сечением, 0≤S_др≤S_{др max}, S_{др max} - максимальная площадь демпфера); P₀ - давление атмосферы; ρ₀ - плотность воздуха атмосферы; F_вн - заранее неизвестная квазистационарная внешняя сила (за время демпфирования изменяется незначительно); F_торм - тормозящая сила из-за избыточного давления в выхлопной камере: F_торм=S(P-P₀); F_тр - сила динамического трения: , где k_тр - коэффициент вязкого трения.

Способ создания адаптивного торможения поршня в пневмоцилиндре осуществляется следующим образом.

Качество торможения задается в виде параметров основной неявной эталонной модели: динамика торможения поршня должна соответствовать динамике движения этой эталонной модели. С помощью двух рекуррентных алгоритмов текущей идентификации на основе измерения положения поршня и давления в выхлопной камере, а также дополнительных расчетов производных производится оценивание неизвестных параметров математической модели движения поршня пневмоцилиндра (первый алгоритм текущей идентификации), а также параметра эффективности управления (второй алгоритм текущей идентификации). На основе оценок, доставляемых первым алгоритмом текущей идентификации, и параметров основной эталонной модели формируется желаемое давление в выхлопной камере. Управление, или величина проходного сечения дросселя, формируется на основе указанного желаемого давления, оценки со второго алгоритма текущей идентификации, указанных выше переменных и дополнительной неявной эталонной модели, формирующей требование по качеству достижения желаемого давления в выхлопной камере. Указанные вычисления могут быть реализованы в микроконтроллере. Особенностью построения адаптивного управления является то, что от алгоритмов текущей идентификации не требуется достижения точных оценок неизвестных параметров (имеются лишь несложно реализуемые ограничения на некоторые оценки), а динамика движения поршня в пневмоцилиндре близка к требуемым характеристикам с первых шагов формирования управления независимо от конкретных значений параметров пневмоцилиндра и внешнего воздействия (в области принципиальной реализуемости такового).

Ниже дано обоснование работы предложенного способа.

В соответствии со вторым законом Ньютона динамика движения поршневой группы определяется балансом сил (без начальных условий):

, или .

А через относительные величины , :

При неизменном количестве газа в рабочей камере (m_г=const) и без обмена тепла с окружающей средой (процесс торможения, как правило, протекает достаточно быстро) термодинамический процесс, связанный с изменением объема V, соответствует адиабатическому, который для воздуха имеет зависимость [Мордасов М.М., Трофимов А.В. Анализ и синтез пневматических устройств. - М.: Машиностроение 1, 2005]:

Для условий убывания газа в выхлопной камере: часть оставшегося газа как часть полного объема соответствует адиабатической закономерности, поэтому эту часть можно описать как:

В соответствии с введенными определениями:

Отсюда уравнение, описывающее динамику убывания воздуха в камере:

В соответствии с [Мордасов М.М., Трофимов А.В. Анализ и синтез пневматических устройств. - М.: Машиностроение 1, 2005] для турбулентного течения газа через дроссель можно записать:

где α_P, ϕ - коэффициенты, зависящие от конструктивных особенностей дросселя. На основании закона идеального газа (считаем давление P не очень высоким, R - газовая постоянная, Т - абсолютная температура) P(t)=ρ(t)RT, отсюда ρ(t)=P(t)/(RT), получим

где - априорно неизвестный коэффициент пропорциональности.

Уравнения (1)-(4) описывают математическую модель пневматического демпфера в рассматриваемых условиях.

Далее для пояснений потребуется еще одна зависимость, которая выводится из предположения, что при работе демпфера скорость изменения переменной гораздо ниже скорости изменения переменных , µ(t). А также на основании (2), по которому и равенств (3), (4):

Или

где

Для синтеза адаптивного закона управления используется алгоритм текущей идентификации, доставляющий неизвестные параметры уравнений (1) и (5), которые запишем в виде (без учета начальных условий):

где a ₁=-k_тр/m, a ₂=SP₀/(mx_max), a ₃(t)=-F_вн(t)/(mx_max), a ₄=-1.4k/(ρ₀Sx_max) - неизвестные коэффициенты и функции времени.

Полученные оценки описываются в виде равенств

где - вектор искомых оценок (верхний индекс «∧» обозначает оценку соответствующего параметра; «т» - транспонирование); - вектор факторных переменных; ε₁ - невязка идентификации, дополняет равенство до точного соответствия.

Дискретный алгоритм текущей идентификации (идентификатор) может быть выбран рекуррентного типа (здесь описан для уравнения (8), для (9) - он подобен и более прост):

где i=1, 2, 3, … - обозначает дискретный момент времени (t_i) определения соответствующей переменной; Г_i - скалярный или матричный коэффициент усиления алгоритма идентификации, выбор которого обозначает соответствующий вид алгоритма, например [Льюнг Л. Идентификация систем. Теория для пользователя: Пер. с англ. / Под ред. Я.З. Цыпкина. - М.: Наука, 1991]:

, 0<γ<2, обычно γ=1 - со скалярным коэффициентом;

, Г₀=γ₀E - рекуррентный метод наименьших квадратов с фактором забывания (γ₀ - большое положительное число, Е - единичная матрица соответствующего размера, 0<<β<1 - назначаемый фактор забывания прошлых измерений).

Любой устойчивый алгоритм текущей идентификации (10), а к ним относятся алгоритмы с указанными коэффициентами усиления, обеспечивает с первых шагов своей работы сходимость модуля невязки идентификации в область, близкую к нулю [Круглов С.П. Вопросы адаптируемости систем управления со схемой «идентификатор + эталон» // Идентификация систем и задачи управления // Tp. IV-й междунар. конф. SICPRO′05 (25-28 января 2005 г., Москва, ИПУ РАН). - М.: ИПУ РАН, 2005. - С. 1307-1348].

Потребуем, чтобы движение поршня в демпфере, описываемое (1), удовлетворяло задаваемой устойчивой неявной основной эталонной модели (неявность заключается в том, что эта эталонная модель существует только в виде этого уравнения):

где - выходная координата эталона, соответствующая ; a _м1, a _м0 - назначаемые параметры эталона, обеспечивающие требуемое движение поршня демпфера в функции от времени (движение, близкое к нисходящей экспоненте).

Если в демпфере обеспечить желаемое значение относительного давления в виде значения

то подстановка его в (8) даст:

что в силу устойчивости эталонной модели и быстрой сходимости к нулю обеспечивает поведение демпфера, близкое эталонному. При этом точные значения оценок не требуются, что соответствует «упрощенным условиям адаптируемости» [Круглов С.П. Вопросы адаптируемости систем управления со схемой «идентификатор + эталон» // Идентификация систем и задачи управления // Tp. IV-й междунар. конф. SICPRO′05 (25-28 января 2005 г., Москва, ИПУ РАН). - М.: ИПУ РАН, 2005. - С. 1307-1348]. Там же определено, что для устойчивости рассматриваемой замкнутой системы управления имеется дополнительное требование:

Так как здесь неизвестно только значение m, то выполнить это ограничение несложно исходя из информации о диапазоне величины m. Вариантом выполнения условия (14) является фиксация оценки по (14) с соответствующей перестройкой алгоритма идентификации (10) на определение лишь двух оценок: и .

Уравнения (6), (8), (10)-(14) соответствуют первой ступени адаптивного закона управления.

Для формирования условия по (12) используется уравнение (7) и оценка по (9). Для этого назначается дополнительная эталонная модель:

соответствующая устойчивому апериодическому звену с единичным коэффициентом усиления и постоянной времени T_м, где на вход поступает , а выходом является . При этом T_м назначается намного меньше времени торможения.

Закон изменения площади дросселя (управление) назначается в виде

Подстановка его в (9) дает

В силу устойчивости дополнительной эталонной модели, малости T_м и ε₂(t) очень быстро достигается условие , а в соответствии с (13) - . При этом параметры пневматического демпфера и внешняя сила заранее неизвестны. Кроме того, в силу подстройки параметров в алгоритме идентификации и, соответственно, закона управления снимаются вопросы относительно приблизительности представленных выше соотношений.

Для устойчивости закона управления (16) здесь также требуется выполнить дополнительное условие, подобное (14):

Его выполнить несложно путем ограничения оценки «сверху» на основании приблизительной априорной информации о конструктивных параметрах демпфера α_P и ϕ либо на основании предварительного оценивания .

Уравнения (7), (9), алгоритм для оценки (аналогичный (10)), (15)-(18) соответствуют второй ступени адаптивного закона управления.

На фиг. 2 представлены результаты модельных компьютерных исследований работы адаптивного демпфера с параметрами (использовался рекуррентный метод наименьших квадратов с фактором забывания): m=7.1 кг, S=3·10^-4 м², x_max=0.05 м, F_вн≈70 H (незначительно меняется по времени), k_тр=30 кг/с, , S_{др max}=10^-5 м², k=2.8·10^-4 с/м, P₀=101000 Па, ρ₀=1.2 кг/м³, a _м1=-151 с^-1, a _м0=-1420 с^-2, T_м=0.01 с, γ₀=1000, β=0.99, шаг временной дискретности 0.001 с, условия (14) и (18) выполняются в виде ограничения соответствующих оценок.

Так как управление торможением производится только стравливанием воздуха из выхлопной камеры , то здесь для создания нужной тормозной силы в начальный период выхлопной дроссель закрыт: и требуемое значение S_др<0 - обеспечить нельзя. На этом этапе идет создание внутри выхлопной камеры достаточного давления. Как только это произойдет: и S_др≥0, начинается активная фаза торможения. В этот момент времени (около 0.07 с) приравниваются значения выхода эталона и его скорости соответствующими значениями демпфера (указано стрелкой). Это вполне справедливо в силу неявности эталонной модели, дает наглядность проверки соответствия между сигналами и .

Следует отметить, что в силу представленных свойств адаптивного пневматического демпфера он способен обеспечить возложенные на него функции только в пределах принципиальной возможности их реализации. Например, точность обработки данных в цифровом вычислителе и скорость отработки управляющего сигнала определяет точность управления; минимальное значение сопротивления выхлопного демпфера (максимальная площадь его проходного сечения) определяет максимально возможную скорость торможения, начальный объем выхлопной камеры - максимальную тормозную силу. Указанные параметры задают область использования адаптивного пневматического демпфера.

Из изложенного также следует, что описанный способ создания адаптивного торможения поршня в пневмоцилиндре также допускает начальное повышение давления в выхлопной камере (как это используется в прототипе). В этом случае для представленного примера будет отсутствовать (сокращен) период начального формирования достаточного давления в выхлопной камере.

Способ создания адаптивного торможения поршня в пневмоцилиндре, отличающийся тем, что при стравливании воздуха величину проходного сечения регулируемого дросселя формируют в зависимости от положения поршня в пневмоцилиндре и давления в выхлопной камере по двухступенчатой схеме адаптивного управления: на первой ступени вычисляют желаемое давление в выхлопной камере на основе оценок неизвестных параметров математической модели движения поршня в пневмоцилиндре, полученных на первом рекуррентном алгоритме текущей идентификации, и параметров основной неявной эталонной модели, предназначенной для задания требуемых характеристик торможения поршня в пневмоцилиндре, на второй ступени формируют величину проходного сечения дросселя на основе желаемого давления в выхлопной камере, оценки эффективности управления дросселем, полученной на втором рекуррентном алгоритме текущей идентификации, и параметра дополнительной неявной эталонной модели, предназначенной для задания качества достижения желаемого давления в выхлопной камере.