Способ формирования s-блока

Способ формирования s-блока

Иллюстрации

Показать все

Реферат

Область техники, к которой относится изобретение

Предполагаемое изобретение относится к области обработки информации и криптографии и, в частности, к способам формирования S-блоков замены с минимальным количеством логических элементов, для последующего использования в аппаратуре систем обработки данных и криптографической защиты информации.

Уровень техники

Операции замены -битовых двоичных векторов на -битовые двоичные вектора, реализуемые в блоках замены (S-блоках), широко используются для криптографического преобразования данных, для сжатия информации и/или защиты от помех при хранении и при передаче информации по каналам связи.

Способы формирования S-блоков с минимальным количеством логических элементов известны и зависят от состава логических элементов схемотехнической реализации.

Так, для набора логических элементов, реализующих логические операции И (&), ИЛИ (V), НЕ (¬), известны метод Квайна-МакКласки, алгоритм Блейка – Порецкого и др. [1]. Однако, известные методы предназначены для оптимизации одной булевой функции, а не набора из булевых функций, задающих S-блок. Кроме того, эти методы неприменимы к набору логических элементов, реализующих логические операции & и XOR (⊕, исключающее ИЛИ).

Известен способ минимизации булевой функции для набора логических элементов {&, ⊕}, предложенный как составная часть процесса запоминания цифровой информации [2]. Однако, этот способ также предназначен для минимизации только одной булевой функции и не учитывает возможности совместной оптимизации нескольких булевых функций, представляющих S-блок. При этом, в данном способе оптимизируется суммарное число элементов & и ⊕ и не принимается во внимание, что схемотехнические затраты на реализацию операций & и ⊕ могут существенно отличаться друг от друга.

Наиболее близким по своей технической сущности к заявляемому является известный способ эффективной реализации S-блока, используемого в стандарте криптографической защиты информации AES [3], в котором, наряду с оптимизацией времени вычисления S-блока, решается и задача минимизации числа логических элементов {&, ⊕} при реализации данного S-блока.

Известный способ [3] выбирается в качестве прототипа.

Основным недостатком прототипа является то, что он предназначен исключительно для S-блоков частного вида, а именно, для S-блоков, задаваемых несколькими (небольшим числом) операций в конечном поле , к которым и относиться S-блок стандарта криптографической защиты AES. Прототип непосредственно опирается на реализацию операции умножения в конечном поле , поэтому он неприменим к произвольному S-блоку, не основанному на какой-либо алгебраической системе.

Другим недостатком (ограничением) прототипа является то, что он осуществляет минимизацию числа логических элементов {&, ⊕} для реализации S-блока в несколько тактов/шагов (для итеративной схемы реализации). При этом число итераций при вычислениях S-блока возрастает с увеличением размера m конечного поля .

Раскрытие изобретения

Техническим результатом предлагаемого способа является

1) уменьшение схемотехнических затрат при реализации S-блока с помощью логических элементов & и ⊕,

2) возможность учета различных схемотехнических затрат на реализацию элементов & и ⊕ в процессе минимизации результирующей логической схемы S-блока.

В заявленном способе также отсутствуют ограничения на значения и размерности S-блока.

S-блок осуществляет замену входного двоичного вектора длины на выходной двоичный вектор длины , где для и .

S-блок однозначно задается аналитически координатными булевыми функциями от переменных , что можно записать в виде

В предлагаемом способе рассматривается представление координатных булевых функций S-блока через приведенные многочлены Жегалкина: каждая функция для аналитически задана в виде

где – множество переменных многочленов , ;

- моном многочлена , который является произведением всех переменных из подмножества множества , причем при для приведенного многочлена .

- мощность (число элементов) множества - мономов , составляющих многочлен .

Существуют и другие, отличные от приведенного многочлена Жегалкина, формы представления булевых функций, например: таблица истинности, дизъюнктивная нормальная форма (ДНФ), конъюнктивная нормальная форма (КНФ). Процессы перехода от одного вида представления к другому хорошо известны. Например, в известном способе [4] приведена последовательность перехода от таблицы истинности к представлению булевой функции через приведенный многочлен Жегалкина. В заявляемом способе не имеет значения, каким образом формируется исходное аналитическое представление S-блока через приведенные многочлены Жегалкина:

Для построения оптимальной логической схемы реализации S-блока через операции & и ⊕ в заявляемом способе используются предварительные аналитические вычисления, использующие операции над множествами. Для получаемого в результате схемотехнического решения не имеет значения, какие используются представления множеств (характеристический вектор, список элементов, в том числе упорядоченный список, и т.д.) и с помощью каких преобразований осуществляются операции над множествами.

Прямой способ реализации S-блока (1), заданного множеством приведенных многочленов Жегалкина , состоит из двух этапов:

1. Составляют множество мономов, входящих в состав многочленов из множества , по формуле

,

где – множество мономов, составляющих многочлен .

Каждый моном реализуют через конъюнкцию & всех элементов множества - подмножества множества входных переменных S-блока, где – множество переменных монома .

2. Каждый многочлен из множества реализуют, как сумму ⊕ выходов из схем реализаций мономов , полученных на предыдущем этапе.

В этом способе схема реализации монома (свободному члену) требует элементов &, где – мощность множества – множества переменных монома .

Аналогично, схема реализации многочлена требует элементов ⊕, где – мощность множества - множества мономов, составляющих многочлен .

Тем самым, аддитивная сложность и мультипликативная сложность реализации множества многочленов составляют:

,

(1)

где – множество мономов, входящих в состав многочленов множества , за исключением свободного члена 1.

Если схемотехнические затраты на реализацию операции & составляют единиц, а затраты на реализацию операции ⊕ - единиц, суммарные затраты на реализацию S-блока составят

(2)

Заявляемый способ состоит из аналитического этапа, на котором выполняется последовательная декомпозиция исходных многочленов, задающих S-блок, на суммы и произведения более простых многочленов, для реализации которых требуется меньше суммарных схемотехнических затрат, этапа синтеза, на котором создаются схемы реализации этих, далее не упрощаемых, многочленов и на основе этих схем в порядке обратном декомпозиции строится итоговая логическая схема реализации S-блока, и третьего этапа, в ходе которого итоговая логическая схема реализуется в электронной схеме.

На каждом шаге декомпозицию множества многочленов осуществляют одним из двух следующих преобразований.

Преобразование 1 определяется парой многочленов из рассматриваемого множества многочленов , и состоит из следующих вычислений:

• выделяют множество общих мономов многочленов и

• вычисляют мощность ;

• если (это равносильно тому, что многочлены и или не имеют общих мономов или имеют ровно один такой моном), то данное преобразование прекращают, так как оно не дает снижения схемотехнических затрат;

• если , то из мономов множества составляют многочлен , а из мономов множеств и – многочлены и соответственно;

• вычисляют, в качестве декомпозиции многочленов и , соотношения

,

,

в которых слагаемые, равные 0, обозначают, что операцию ⊕ реализовывать не требуется;

• формируют результирующее множество многочленов

• вычисляют эффективность преобразования (величину уменьшения схемотехнических затрат) в виде

Преобразование 2 определяется параметром – переменной из множества и состоит из следующих вычислений для каждого многочлена из рассматриваемого множества многочленов :

• для рассматриваемого многочлена формируют множество мономов, содержащих переменную

• вычисляют мощность множества ;

• если (это равносильно тому, что многочлен или не зависит от переменной , или имеет ровно один моном, содержащий переменную ), то не подвергают декомпозиции, в неизменном виде включают в результирующее (формируемое) множество многочленов , а сложность его декомпозиции полагают равной нулю;

• если , то осуществляют декомпозицию многочлена , выполняя следующие действия:

◯ из мономов множества исключают переменную и формируют многочлен

,

причем моном , состоящий из единственной переменной , переходит в свободный член 1 многочлена ;

◯ из мономов множества (мономов многочлена , не содержащих переменную ) формируют многочлен

◯ вычисляют многочлен

◯ приводят подобные члены в (исключают повторяющиеся мономы)

◯ если число мономов многочлена меньше числа мономов многочлена на 2 и более, что равносильно условию на мощности множеств

,

то в качестве декомпозиции многочлена используют выражение

,

▪ включают в результирующее множество многочленов многочлены , и ;

▪ принимают значение сложности декомпозиции многочлена равной , если , то увеличивают значение на

;

◯ если же

,

то в качестве декомпозиции многочлена используют выражение

,

▪ включают в результирующее (формируемое) множество многочленов многочлены и ;

▪ принимают значение сложности декомпозиции многочлена равной , если , то увеличивают значение на

Эффективность преобразования 2 (величину уменьшения схемотехнических затрат) для рассматриваемого множества многочленов и переменной рассчитывают по формуле:

,

где значения и вычисляются по формулам (1) и (2).

Для минимизации схемотехнических затрат на реализацию мономов из множества проводят разложение мономов в произведение мономов с меньшим числом переменных, используя следующее преобразование.

Преобразование 3 состоит из следующих вычислений и операций:

• осуществляют во множестве мономов поиск для обнаружения пары мономов , причем , с наибольшим числом общих переменных, путем последовательного перебора, то есть находят пару мономов с максимальным значением

где – множество переменных в мономе

• если (это равносильно тому, что у мономов рассматриваемого множества нет общих переменных), то завершают преобразование

• если , то выполняют следующие действия:

• составляют мономы , , из переменных , и , соответственно; в качестве разложения мономов и используют выражения

,

,

в которых сомножители, равные 1, обозначают, что операцию & реализовывать не требуется;

• формируют результирующее множество мономов , удаляя из множества мономы и и добавляя мономы , , , т.е. вычисляют

Предлагаемый способ минимизации схемотехнических затрат на реализацию S-блока, заданного многочленами Жегалкина , состоит из 7 этапов.

1. Исходное множество многочленов

последовательно преобразовывают с использованием преобразований 1 и 2:

где каждый переход имеет эффективность больше нуля (т.е. приводит к снижению оценки суммарных схемотехнических затрат и осуществляется к результирующему множеству многочленов, формируемому в ходе этих преобразований). Результирующее множество характеризуется тем, что никакое из преобразований 1 и 2 не приводит к дальнейшему снижению оценки затрат ни при каких параметрах.

2. Затем, по результирующему множеству формируют множество мономов , входящих в многочлены множества и добавляют к нему множество входных переменных

,

где – множество мономов, составляющих многочлен .

3. Затем осуществляют разложение мономов множества , многократно используя преобразование 3 до тех пор, пока преобразование станет неприменимым, и получают последовательность множеств

Поскольку переменные не удаляют в процессе преобразования множества мономов, то невозможность применения преобразования 3 к множеству равносильно тому, что состоит только из элементов , которые и являются входами S-блока.

4. Построение логической схемы S-блока начинают проходом по цепочке в обратном порядке, соединяя операцией & выходы схем мономов, участвующих в разложении, схемы которых, в свою очередь, были составлены на предыдущих шагах.

5. После построения логических схем мономов из множества формируют логические схемы многочленов из множества , соединяя операцией ⊕ выходы схем мономов , составляющих этот многочлен.

6. Далее осуществляют проход по цепочке в обратном порядке, и составляют логические схемы очередных многочленов, соединяя операциями & и ⊕ выходы схем предшествующих многочленов в соответствии с формулами декомпозиции.

7. Выходы логических схем многочленов множества используют в качестве выходов логической схемы S-блока.

В описанном способе минимизации схемотехнических затрат не специфицированы параметры, которые используются для переходов и . Однако, от выбора этих параметров зависит получаемый эффект снижения схемотехнических затрат. Эффективный метод выбора наилучшего набора параметров, обеспечивающих наименьшее из возможных значений суммарных схемотехнических затрат, неизвестен, а полный перебор всех наборов требует экспоненциальных вычислительных затрат от величины , что делает перебор неприемлемым для практически интересных значений .

В заявляемом способе предлагается выбирать параметры перехода так, чтобы на каждом переходе и уменьшение оценки схемотехнических затрат было максимально возможным, а среди параметров, обеспечивающих такое снижение оценки, использовать параметры, запись (представление) которых предшествует записям остальным в лексикографическом порядке.

Необходимо отметить, что построение (формирование) логической схемы, реализующей соответствующую булеву функцию, является известным процессом (этот процесс описан, например, в [1, 4]).

Реализация электронной схемы на основе полученной логической схемы также является известным процессом и может быть выполнена как на дискретных элементах, так и с использованием интегральных микросхем, в том числе программируемых логических интегральных микросхем (ПЛИС), по выбору разработчика.

Краткое описание чертежей

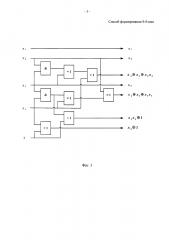
На фиг. 1 показана начальная логическая схема для примера реализации способа.

На фиг. 2 показана промежуточная логическая схема для примера реализации способа.

На фиг. 3 показана промежуточная логическая схема для примера реализации способа.

На фиг. 4 показана промежуточная логическая схема для примера реализации способа.

На фиг. 5 показана промежуточная логическая схема для примера реализации способа.

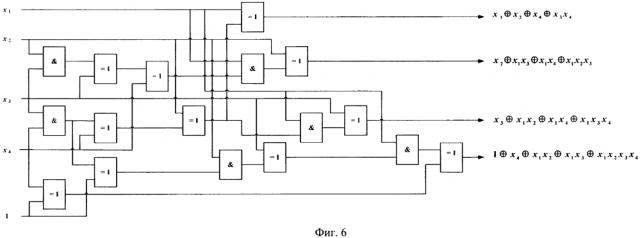
На фиг. 6 показана финальная логическая схема для примера реализации способа.

Осуществление изобретения

Рассмотрим пример реализации предложенного способа для S-блока, имеющий = 4 входов и = 4 выходов и заданного следующими многочленами Жегалкина от четырех переменных

Прямой способ реализации этого S-блока требует 11 операций & для формирования мономов , , , , , и 13 операций для составления из них многочленов.

Рассмотрим применение предлагаемого способа в условиях, когда схемотехнические затраты на реализацию операций & и ⊕ совпадают, т.е. = = 1.

Число общих мономов у любой пары многочленов не превышает 1, поэтому способ из прототипа не дает выигрыша по количеству операций, т.е. не приводит к снижению схемотехнических затрат.

В предлагаемом способе этому S-блоку соответствуют исходные значения:

У любых двух многочленов из множества совпадает не более одного монома, что при на этапе А1 (согласно обозначению в формуле изобретения), соответствует тому, что . Поэтому на этапе А1 после присвоения значения выполняют переход на этап А2, где вычисляют значение , характеризующую сложность прямой реализации множества многочленов

и величину имеющегося снижения сложности

С этапа А3 до этапа А4 по очереди перебирают переменные из множества . Для выбранного значения каждый многочлен из представляют в одном из 2-х вариантов:

или

,

в записи которого меньше операций . Для полученного разложения многочленов по переменной подсчитывают значение , характеризующую снижение сложности прямой реализации множества многочленов за счет перехода к прямой реализации выделенных компонент разложения с последующим составлением исходных многочленов по выбранным формулам.

Для рассматриваемого множества многочленов перебор переменных дает следующие результаты разложения многочленов и соответствующие им оценки сложности использования такого разложения:

Для :

сложность

Для :

сложность

Для :

сложность

Для :

сложность

Наибольшее снижение сложности (значение ) имеет место при . Поэтому на этапе А4 при переходе на этап А1 при :

Для множества многочленов максимальная общая часть двух многочленов состоит из 3-х мономов , , . Поэтому при переходе на этап А2 вычисляемые параметры имеют значения:

На этапе А2 вычисляют сложность прямой реализации множества многочленов

и снижение сложности за счет выделения общего слагаемого

На этапах с А3 по А4 разложение многочленов множества по переменным , , из множества дает следующие оценки сложности использования данного разложения по сравнению с сложностью прямой реализации множества

Для :

сложность

Для :

сложность

Для :

сложность

Наибольшее снижение сложности (значение ) имеет место при , что меньше снижения сложности (значение ) при выделение многочлена .

Поэтому на этапе А4 при переходе на этап А1 при вычисляемые параметры имеют следующие значения:

Число общих мономов у любой пары многочленов из множества не превышает 1, поэтому при переходе на этап А3 при вычисляемые параметры имеют следующие значения

и сложность прямой реализации

На этапах с А3 по А4 разложение многочленов мно