Способ передачи информации и система для его осуществления

Способ передачи информации и система для его осуществления

Иллюстрации

Показать все

Реферат

Изобретение относится к телеметрии, технике связи и может быть использовано в системах передачи данных по каналам связи. Его использование позволяет повысить достоверность передачи информации без введения структурной избыточности в передаваемые сообщения, обнаруживать возникающие при передаче ошибки, как одиночные, так и кратные, повысить скорость передачи информации.

Это достигается путем структурно-алгоритмических преобразований (САП), которые осуществляют при передаче телеметрической информации (ТМИ) на борту контролируемого объекта (в этом случае САП называют «прямыми» (ПСАП)) и при ее приеме (реализуемые при этом САП называют «обратными» (ОСАП)).

Наиболее близким к предлагаемому изобретению является способ дискретной передачи информации ([1], патент RU №2434301 от 20.11.2011, бюл. №32). В нем также в результате структурно-алгоритмических преобразований (САП), предшествующих передаче информации, формируют последовательность слов-измерений или сообщений, называемых «выборками первичных сигналов», которые преобразуют в выборки с меньшей разрядностью представления исходных значений. Сформированные выборки с меньшей разрядностью представления исходных значений являются образами-остатками b_i. Основу изобретения [1] составляет замена традиционного позиционного представления слов двоичных 2n-разрядных слов-измерений X на их отображение образами-остатками b_i. В соответствии с математической моделью образы-остатки b_i. получают в результате выполнения операций, соответствующих делению X на определенным образом выбранные модули сравнения m_i. В результате этого обеспечивают выполнение требований тождественного равенства исходного сообщения X

и его образа-остатка b_i, получающего в результате операции, эквивалентной арифметической операции деления Х на модуль сравнения m_i:

Таким образом, способ [1] представляет собой инженерную интерпретацию математической модели (1).

Способ-прототип [1] заключается в том, что на передающей стороне формируют первичный сигнал, шкала значений которого в 2²ⁿ раз превышает максимально допустимое значение погрешности, формируют последовательность выборок первичного сигнала путем его дискретизации с выбранной частотой опроса, формируют последовательность передаваемых выборок путем преобразования последовательности выборок первичного сигнала, передают сформированную последовательность выборок по каналу связи на приемную сторону, на приемной стороне принимают полученную последовательность выборок, формируют восстановленную последовательность выборок первичного сигнала путем преобразования принятой последовательности выборок, восстанавливают первичный сигнал путем фильтрации последовательности выборок первичного сигнала, отличающийся тем, что на передающей стороне преобразование последовательности выборок первичного сигнала в последовательность передаваемых выборок осуществляют следующим образом: формируют 2ⁿ равномерно распределенных в пределах шкалы значений первичного сигнала пороговых уровней u_i, сравнивают значение каждой выборки первичного сигнала со значениями всех пороговых уровней, определяют значение максимального из превышенных пороговых уровней, преобразуют значение каждой выборки первичного сигнала путем вычитания из него значения максимального из превышенных пороговых уровней, при этом на приемной стороне преобразование принятой последовательности выборок в восстановленную последовательность выборок первичного сигнала осуществляют следующим образом: определяют приращение значения каждой принятой выборки

путем вычитания из него значения предшествующей принятой выборки, формируют минимальный ненулевой пороговый уровень, значение которого в 2ⁿ раз меньше шкалы значений первичного сигнала, сравнивают модуль приращения значения каждой принятой выборки с половиной значения минимального ненулевого порогового уровня, при превышении модуля приращения значения каждой принятой выборки половины значения минимального ненулевого порогового уровня и при отрицательном значении указанного приращения значение каждой восстановленной выборки первичного сигнала определяют путем суммирования приращения значения соответствующей принятой выборки, значения предшествующей восстановленной выборки первичного сигнала и значения минимального ненулевого порогового уровня, при превышении модуля приращения значения каждой принятой выборки половины значения минимального ненулевого порогового уровня и при положительном значении указанного приращения значение каждой восстановленной выборки первичного сигнала определяют путем суммирования приращения значения соответствующей принятой выборки и значения предшествующей восстановленной выборки первичного сигнала и вычитания из полученной суммы значения минимального ненулевого порогового уровня, при превышении половины значения минимального ненулевого порогового уровня модуля приращения значения каждой принятой выборки значение каждой восстановленной выборки первичного сигнала определяют путем суммирования приращения значения соответствующей принятой выборки и значения предшествующей восстановленной выборки первичного сигнала [1].

Отличительная особенность известного способа [1] заключается в том, что вместо математической операции сравнения значений результатов измерений X по модулю m_i, предполагающей операцию деления и нахождения образов-остатков b_i, используют результаты превышения значениями X пороговых уровней u_i. При превышении каждого из пороговых уровней

непрерывный счет значений сообщений X по мере их возрастания или убывания обрывают и возобновляют с 0. Поэтому получающиеся значения оказываются ограниченными по уровню значением разности между порогами Δ_ui=u_j+1-u_i, что эквивалентно образам-остаткам b_i, которые были бы получены в результате арифметической операции деления. Это означает, что сформированные таким образом значения от 0 до (Δ_ui-1) совпадают со значениями образов-остатков b_i при условии, что Δ_ui=m_i. Такая формулировка модели (1) на инженерном языке позволила определить новый способ восстановления выборок или слов-измерений при приеме сообщений. Он описан в формуле изобретения [1], когда рассматривается приемная сторона. Однако замена модулей m_i. разностями между порогами сравнения Δ_ui. оказывается сложной при большом числе используемых модулей сравнения. В результате этого возможности инженерного синтеза новых способов восстановления данных измерений при использовании структурно-алгоритмических преобразований (САП) становятся все более ограниченными по мере увеличения числа различных модулей сравнения m_i.

В этом случае более полезным с точки зрения реализации новых идей повышения помехоустойчивости передаваемых данных становится математический синтез новых технических решений на основе модели, представленной в виде системы остаточных классов (СОК) (системы сравнений, определяемой формулой (2)):

где X_j - j-тое слово-измерение (сообщение);

m₁, m₂ - модули сравнения, если n - половина исходной разрядности N=2n (разрядной сетки) представления исходных традиционных слов-измерений, то случай оптимального их выбора представлен значениями m₁=2ⁿ-1, m₂=2ⁿ+1;

b_1j, b_2j - образы-остатки слова-измерения (сообщения) X_j, полученные в результате операции деления X_j на модули сравнения m₁ и m₂, соответственно.

Так, в случае исходного байтового представления слов-измерений (2n=8) m₁=2⁴-1=15, а m₂=2⁴+1=17. Если 2n=10, что соответствует случаю 10-тиразрядного представления значений телеметрируемых параметров (ТМП), то m₁=2⁵-1=31, а m₂=2⁵+1=33. Сформированные при таком подходе образы-остатки для однозначного их отображения могут иметь n - разрядную позиционную структуру представления. Однако некоторое исключение из этого правила составляют результаты кодирования образов-остатков, полученных при сравнении по модулям m₂=2ⁿ+1.

При предлагаемом дополнительном кодировании новые сообщения получают в результате замены исходных значений X_j, j=0, 1, 2, 3, … на сообщения C_j, j=0, 1, 2, 3, …, составленные, например, из значений образов-остатков

Здесь подстрочные индексы s (< >₁₀ и < >₂) определяют систему счисления - десятичную и двоичную, соответственно.

Например, если первое значение слова-измерения равно: Х₁=<116>₁₀=<01110100>₂ при восьмиразрядном представлении двоичного кода (2n=8), то при модулях сравнения mod 15 и mod 17 результатом дополнительного помехоустойчивого кодирования будет значение С₁⇔<b₁₁(mod 15),b₂₁(mod 17)>_s,s=2,10. В рассматриваемом случае это значение С₁=<10111110>₂=<190>₁₀. Первый подчеркнутый образ-остаток равен: b₁₁=<1011>₂=<11>₁₀, что соответствует результату деления значения 116 на модуль сравнения 15: 116=15×7+11. Второй четырехразрядный образ-остаток (n=4) b₂₁=<1110>₂=<14>₁₀, что соответствует результату деления значения 116 на модуль сравнения 17: 116=17×6+14.

Таким образом, при традиционном способе передачи информации значению X_j может быть поставлен в полное соответствие его эквивалент в виде: m₁×l₁+b_1j или в виде: m₂×l₂+b_2j, где m₁, m₂ - модули сравнения, a l₁, l₂ - значения неполных частных, получающихся при делении.

При представлении данных их образами-остатками (2) передаче подлежат только значения b_1j и b_2j, при этом информация о m₁, m₂ и о l₁, l₂ из передачи исключается. В этом случае m_l, m₂ могут рассматриваться как ключевые данные, известные пользователю, а l₁, l₂, как данные, которые восстанавливают при приеме на основе принятых значений образов-остатков b_1j и b_2j.

Результат дополнительного кодирования C₁ представляет, таким образом, сжатую форму представления передаваемых данных, поскольку в новых закодированных значениях отсутствует информация о модулях сравнения m₁ m₂ и «неполных частных» l₁, l₂, равных, например, при m₁=15 и m₂=17, l₁=7 и l₂=6, соответственно. При традиционном кодировании информация о m₁=15 и m₂=17 и о «неполных частных» l₁=7 и l₂=6 присутствует в неявном виде. Теория конечных полей Э. Галуа утверждает, что информация о «неполных частных» l_i может быть восстановлена при условии, что выбранные модули сравнения m₁ и m₂ не будут иметь других совместных делителей, кроме 1 ((m₁, m₂)=1) ([2], И.М. Виноградов «Основы теории чисел», М.: Наука, 1972 г.). Поэтому результат кодирования с использованием алгоритма (3) обладает следующими сущностными признаками:

- он является «безызбыточным» за счет того, что разрядность представления дополнительно закодированных данных C_j остается, в основном, неизменной и равной, например, 2n=8 или 2n=10, но, с другой стороны, за счет сжатой формы представления данных с исключением информации о модулях сравнения m₁ m₂ и «неполных частных» l₁, l₂, создана дополнительная внутренняя избыточность ТМИ, что, в итоге, приводит к повышению информационной нагрузки каждого двоичного символа;

- увеличено в 2ⁿ+1 раз минимальное кодовое расстояние между соседними значениями данных телеизмерений, благодаря чему обеспечена возможность обнаружения и исправления ошибок передачи данных телеизмерений.

Эффект увеличения минимального кодового расстояния можно пояснить на следующем примере.

Если взять соседние значения данных телеизмерений для случая 2n-8, например, Х₁=<115>₁₀=<01110011>₂ и Х₂=<116>₁₀=<01110100>₂, то при традиционных способах их представления кодовое расстояние между ними будет равно d_min^(тр)=1. При этом в соответствии с теорией помехоустойчивого кодирования отсутствует возможность обнаружения ошибок передачи ТМИ ([3], Зюко А.Г. Помехоустойчивость и эффективность систем связи. - М.: Связь, 1972. - 360 с.).

При кодировании выбранных значений в соответствии с алгоритмом (3) и использовании модулей сравнения m₁=15 и m₂=17, получим: С₁=<10101101>₂=<173>₁₀ и С₂=<10111110>⁹=<190>₁₀. В результате минимальное кодовое расстояние увеличилось в k=2ⁿ+1 раз и стало при n=4, равным d_min^(СОК)=17. В результате этого обеспечивается возможность обнаружения и исправления ошибок передачи ТМИ. Увеличение минимального кодового расстояния (d_код) в 17 раз в соответствии с теорией помехоустойчивого кодирования обеспечивает возможность исправления до 4 ошибок передачи значений ТМП ([3]).

Однако у такого способа представления есть недостаток, заключающийся в том, что в общем случае для однозначного представления значений образов-остатков по модулям m₂=2^m+1 требуется не n, а (n+1) разрядов двоичного кода (в случае, когда 2n=8, пять разрядов). Если, например, при 2n=8 не ввести дополнительной избыточности в виде дополнительного

9 двоичного разряда и ограничиться n=4 при представлении значений b_2i, то окажутся неразличимыми кодовые конструкции <0>₁₀ и <135>₁₀, а также <16>₁₀ и <136>₁₀. Это приведет к дополнительно привнесенным ошибкам. Хотя, в итоге, этот недостаток и перекрывается достигаемым техническим эффектом, получаемым при приеме за счет обнаружения и исправления ошибок передачи ТМИ в режиме «мягкого» декодирования, однако потенциальные возможности повышения помехоустойчивости данных телеизмерений не будут достигнуты.

Этот недостаток устранен при использовании предлагаемого изобретения. Предлагаемый способ предлагает одну из реализаций безызбыточного дополнительного помехоустойчивого кодирования с использованием образов-остатков. Особая практическая значимость безызбыточного дополнительного помехоустойчивого кодирования заключается в том, что его реализация не требует изменения существующей структуры телеметрических кадров и доработки уже существующей телеметрической аппаратуры или системы связи. Поэтому предлагаемый способ является щадящим по отношению к существующей практике. Он также может быть реализован программными методами путем перепрограммирования программируемых логических интегральных схем (ПЛИС), сигнальных процессоров и микроконтроллеров, на основе которых созданы существующие и разрабатываются перспективные бортовые радиотелеметрические системы (БРТС) и системы связи.

Сущностные характеристики предлагаемого способа заключаются в следующем. Он предполагает использование ПСАП на передающей стороне, которое представляет собой дополнительное кодирование значений слов-измерений, которые получают на выходе цифровых датчиков или аналого-цифровых преобразователей (АЦП). Его основу составляет деление слов-измерений или сообщений, представленных на выходе цифровых датчиков или АЦП N-разрядным двоичным кодом, на составные части или кодовые сегменты, которые затем переставляют местами с сохранением прежней разрядности слов-измерений или сообщений. При этом число N может быть как четным, например, N=2n (этот пример был рассмотрен ранее), так и нечетным, N=2n+1.

В первом случае, когда N=2n - четное число, примером базового ПСАП, максимизирующего число исправленных ошибок передачи ТМИ при неизменном d_min^(Пер)=2ⁿ (если N=2n=8, то d_min^(Пер)=2⁴=16), может быть деление исходных слов-измерений, представленных N-разрядным двоичным кодом на старшее (a_2i) и младшее (a_1i) полуслова с сохранением традиционной позиционной системы их представления двоичным кодом с вдвое меньшей разрядностью (n).

Алгоритм кодирования исходных слов-измерений и сообщений, ориентированный на приведенный пример,

предполагает перестановку местами старшего (a_2j) и младшего (a_1j) полуслов или старшего (a_2j) и младшего (a_1j) кодовых сегментов:

где C_j - результат дополнительного безызбыточного помехоустойчивого кодирования слов-измерений и сообщений X_j.

Однако в общем случае результатами деления исходной кодовой конструкции слова-измерения или сообщения могут быть не только полуслова, но и другие ее составные части или кодовые сегменты. Например, при нечетном N (N=2n+1) возможны следующие два базовых варианта деления:

1) старшая часть (a_2j), состоящая из (n+1) двоичного разряда, и младшая часть (a_1j), представляемая n-разрядным традиционным позиционным двоичным кодом;

2) старшая часть (a_2j), состоящая из n двоичных разрядов, и младшая часть (a_1j), представляемая (n+1) - разрядным традиционным позиционным двоичным кодом.

Также возможны и другие варианты деления исходной двоичной кодовой конструкции на составные части или кодовые сегменты.

Различие между рассмотренными выше примерами дополнительного кодирования на основе различной разрядности сегментов будет проявляться в значениях минимального кодового расстояния d_min. Так, например, в первом случае d_min⁽¹⁾=2⁽ⁿ⁺¹⁾, а во втором d_min⁽²⁾=2ⁿ.

Этот эффект продемонстрируем на следующих примерах. Пусть N=2n+1=9, что возможно при n=4. При этом X₁=<115>₁₀=<001110011>₂ и Х₂=<116>₁₀=<001110100>₂. Тогда для X₁=<115>₁₀ при первом варианте перестановки старшая часть (a_2j), равная a_2j=<00111>₂ и состоящая из 5 двоичных разрядов, и младшая часть (a_1j)=<0011>₂, представляемая 4-хразрядным традиционным позиционным двоичным кодом, должны быть переставлены местами С₁⁽¹⁾=<001100111>₂=<103>₁₀. Для Х₂=<116>₁₀=<001110100>₂ результат дополнительного кодирования приведет к следующему значению: С₂⁽¹⁾=<010000111>₂=<135>₁₀. Кодовое расстояние между ними равно: d_min⁽¹⁾=|С₁⁽¹⁾-С₂⁽¹⁾|=2⁽ⁿ⁺¹⁾=32 при n=4.

Второй вариант перестановки приведет к следующим значениям:

С₁⁽²⁾=<100110011>₂=<307>₁₀ и С₂⁽²⁾=<101000011>₂=<323>₁₀.

Кодовое расстояние между ними равно: d_min⁽²⁾=|С₁⁽²⁾-С₂⁽²⁾=2ⁿ=16 при n=4.

С точки зрения математического описания предлагаемого дополнительного кодирования информации с использованием теории конечных полей младшее полуслово (a_1j) представляет собой остаток (b_3j) (a_1j=b_3j) по модулю m₃, равному значению минимального кодового расстояния m₃⁽¹⁾⁼2⁽ⁿ⁺¹⁾ в первом случае и m₃⁽²⁾=2ⁿ во втором случае:

где индексы b₃ и m₃, равные i=3, выбраны с учетом предшествующей формулы (2), в которой индекс i=1, соответствует модулю сравнения m₁=2ⁿ-1, а индекс i=2 - модулю сравнения m₂=2ⁿ+1.

Перестановка полуслов или других составных частей или кодовых сегментов исходной кодовой конструкции слов-измерений в условиях, когда минимальное кодовое расстояние d_min увеличено по сравнению традиционной передачей информации, а разрядная сетка для представления результатов дополнительного кодирования осталась прежней N-разрядной, приводит к следующему продолжению математической постановки задачи изобретения - повторному сравнению результатов кодирования C_j по модулю N.

Таким образом, в предлагаемом способе также использованы две операции сравнения: первая, представленная формулой (6) - по модулю m₃, и вторая, представленная формулой (7) - по модулю N.

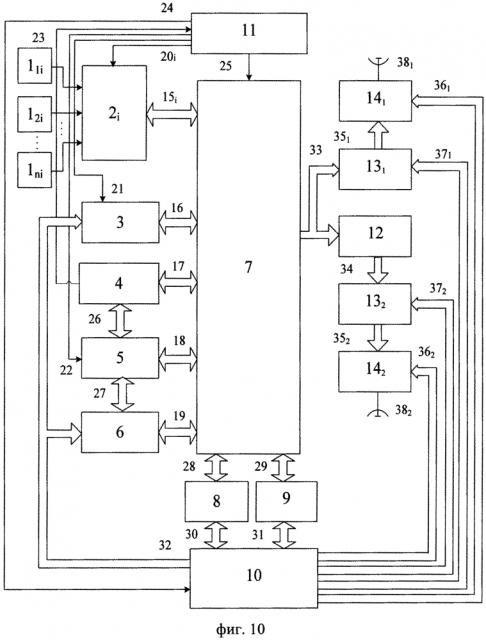
В результате этого исходное графическое отображение телеметрируемого параметра (ТМП), представленное на фиг. 1, преобразуют перед передачей ТМИ к виду, приведенному на фиг. 2.

Алгоритмы восстановления переданных значений при приеме ТМИ, предполагающие использование обратного структурно-алгоритмического преобразования (ОСАП), ориентированы на следующие два типа декодирования, условно называемые «жесткое» и «мягкое». При этом под «жестким» декодированием понимают операцию восстановления первоначальных значений телеизмерений без исправления ошибок путем обратной перестановки составных частей или кодовых сегментов, разрядность которых известна на приемной стороне.

Цель использования алгоритма «жесткого» декодирования заключается в том, чтобы обеспечить восстановление информации в самом общем случае, в том числе и при отсутствии корреляционной взаимосвязи между

соседними отсчетами ТМП, с погрешностью, которая была бы не хуже той, что получают при использовании существующей практики передачи результатов телеизмерений. Дополнительное назначение алгоритма «жесткого» декодирования также заключено в том, чтобы пользователь имел возможность увидеть то качество приема ТМИ, которое получают при использовании существующей практики телеизмерений. Такой подход направлен, помимо прочего, на устранение психологической неуверенности той части специалистов, которые плохо усваивают различные новшества.

Цель использования алгоритма «мягкого» декодирования состоит в том, чтобы обнаружить и исправить ошибки передачи в закодированных значениях ТМП.

При этом под «мягким» декодированием понимают последовательность следующих операций: выделения графических фрагментов данных дополнительного кодирования, заключенных между соседними максимальными значениями абсолютных разностей δ_jM=|C_j-C_(j+1)|≥0,8×2^N, и δ_(j+s)M=|C_(j+s)-C_(j+s)+1|≥0,8×2^N), равными или большими значений (0,8×2^N), где C_j - результат дополнительного безызбыточного помехоустойчивого кодирования j-того по принятому порядку счета слова-измерения или сообщения X_j, a δ_jM=|C_j-C_j+1| и δ_(j+s)M=|C_(j+s)-C_(j+s)+1| - соседние максимальные значения абсолютных разностей между результатами дополнительного безызбыточного помехоустойчивого кодирования слов-измерений или сообщений C_j, C_j+1, определяющие начало графического фрагмента, и C_(j+s), C_(j+s)+1, определяющие окончание графического фрагмента, включающего в себя s выборок закодированных на основе перестановки составных частей значений телеметрируемых параметров, N-число разрядов слов-измерений или сообщений X_j.

Таким образом, предлагаемый способ заключается в том, что на передающей стороне осуществляют сбор сигналов от источников сообщений, преобразуют их в двоичный код, обеспечивают синхронизацию сформированных

слов-измерений и формируют из них уплотненный цифровой групповой сигнал, подлежащий передаче по каналам связи.

От известных аналогов он отличается тем, что на передающей стороне кодовые конструкции, сформированные на первом этапе кодирования слов-измерений или сообщений, разделяют на полуслова с равным числом двоичных разрядов, в том числе на другие части или кодовые сегменты, имеющие различное число разрядов при их представлении двоичным кодом, которые затем переставляют их местами с сохранением прежней разрядности представления слов-измерений или сообщений, но с получением их новых значений, сформированные слова-измерения или сообщения расставляют в уплотненном групповом телеметрическом сигнале в определенной последовательности по отношению к сигналам синхронизации, сформированный таким образом уплотненный групповой телеметрический сигнал подвергают последующей модуляции и передаче, а на приемной стороне принимают полученную последовательность переданных символов двоичного кода, формируют восстановленную последовательность слов-измерений или сообщений, осуществляют параллельное их декодирование с использованием «жесткого» и «мягкого» декодеров, при этом в результате операции «мягкого» декодирования определяют графические фрагменты закодированных на основе перестановки составных частей или кодовых сегментов первоначальных значений телеметрируемых параметров, заключенные между соседними максимальными значениями абсолютных разностей δ_jM=|C_j-C_(j+1)|≥0,8×2^N, и δ_(j+s)M=(C_(j+s)-C_(j+s)+1|≥0,8×2^N), равными или большими значений 0,8×2^N, где C_j - результат дополнительного безызбыточного помехоустойчивого кодирования j-того по принятому порядку счета слова-измерения или сообщения X_j, a δ_jM=|C_j-C_j+1| и δ_(j+s)M=|C_(j+s)-C_(j+s)+1| - соседние максимальные значения абсолютных разностей между результатами дополнительного безызбыточного помехоустойчивого кодирования слов-измерений или сообщений C_j, C_j+1, определяющие

начало закодированного графического фрагмента, и C_(j+s), C_(j+s)+1, определяющие окончание графического фрагмента, включающего в себя s выборок закодированных на основе перестановки составных частей значений телеметрируемых параметров, при этом N - это число разрядов, которые используют для представления слов-измерений или сообщений X_j, обеспечивают обнаружение и исправление ошибок передачи значений телеметрируемых параметров на основе групповых свойств «равноостаточности», которые должны быть постоянными при отсутствии ошибок передачи информации в выделенных закодированных графических фрагментах телеметрируемого параметра, преобразованного при дополнительном помехоустойчивом кодировании на передающей стороне, а в результате операции «жесткого» декодирования осуществляют восстановление первоначальных результатов телеизмерений без исправления ошибок путем обратной перестановки составных частей, разрядность которых известна на приемной стороне, осуществляют сглаживание или фильтрацию восстановленных в результате «жесткого» декодирования данных и по отношению к вычисленным соседним значениям телеизмерений определяют их разности, которые при выполнении операций «мягкого» декодирования с учетом разрешенных позиций для значений принятого безызбыточного помехоустойчивого кода используют в качестве допусков при выборе наиболее подходящих, кондиционных значений восстанавливаемых данных телеизмерений, определяемых в соответствии с принятым критерием достоверности, производят повторное «жесткое» декодирование данных телеизмерений, скорректированных в результате операций «мягкого» декодирования, сглаженные или отфильтрованные данные, полученные при первой операции «жесткого» декодирования сравнивают с синхронными, совпадающими по времени опроса, значениями, полученными в результате второй операции «жесткого» декодирования, результаты сравнения используют для оценивания достигаемого технического эффекта в виде оценок повышения показателей достоверности приема телеметрической информации, а также для сравнения полученных результатов и корректировки значений сглаживания или фильтрации данных телеизмерений, полученных при первом «жестком» декодировании, определяют их близость к другим разрешенным позициям помехоустойчивого кода, сформированного при дополнительном кодировании телеметрируемого параметра на передающей стороне, в результате чего реализуют расширенные возможности, используемые для контроля достоверности полученных результатов телеизмерений и информационной поддержки принятия решений.

Предлагаемый способ также отличается тем, что при выполнении операций «мягкого» декодирования принятые с ошибками данные телеизмерений, преобразованные на передающей стороне с использованием дополнительного кодирования результатов телеизмерений, приводящих к дополнительному безызбыточному помехоустойчивому кодированию и принадлежащие выделенным графическим фрагментам преобразованных телеметрируемых параметров, подвергают делению на первый модуль сравнения m₃, равный реализованному в результате дополнительного помехоустойчивого кодирования минимальному кодовому расстоянию d_min=2ⁿ при N=2n или d_min=2^n+k при N=2n+k, где N - число двоичных разрядов в исходном двоичном коде слов-измерений или сообщений, k=0, 1, 2, в результате чего находят целочисленные остатки от деления, строят гистограмму распределения их значений и в качестве инварианта, проявляющегося в виде постоянства значения группового свойства «равноостаточности», наблюдаемого в пределах выделенного графического фрагмента, выбирают в сформированной статистической выборке, состоящей из остатков, полученных в результате операции деления на первый модуль сравнения m₃, наиболее часто встречающееся значение, которое рассматривают в качестве кандидата в инварианты, при этом все другие значения остатков, не совпадающие со значением найденного кандидата-инварианта, используют

в качестве признака обнаружения ошибок передачи результатов телеизмерений, которые исправляют путем подстановки вместо них данных, достоверность которых подтверждают тем, что они при делении на первый модуль сравнения m₃ дают значение остатка, равное установленному значению кандидата-инварианта, найденному для выделенного графического фрагмента, выбирают среди выделенных преобразованных данных телеизмерений значения, принадлежащие наиболее близким по абсолютной величине разрешенным позициям сформированного на передающей стороне дополнительного помехоустойчивого кода, которые отстоят друг от друга на величину, равную lm₃, m₃=d_min, l=1, 2, 3, …, где d_min - минимальное кодовое расстояние реализованного на передающей стороне дополнительного помехоустойчивого кода, при выполнении условия, что величины различий принятых данных от их номинальных значений, определяемых априорно известными разрешенными позициями реализованного на передающей стороне дополнительного помехоустойчивого кода, не выходят за пределы допусков, которые устанавливают на основе результатов «жесткого» декодирования принятых сигналов и последующего их сглаживания или фильтрации на основе различных способов сглаживания или фильтрации.

Представление о техническом эффекте, который получают при реализации способа, дают иллюстрации, приведенные на фиг. 1, фиг. 2, фиг. 3 и фиг. 4.

На иллюстрации, представленной на фиг. 1, показано графическое отображение ТМП, смоделированного в виде синусоидального изменяющегося напряжения, при его представлении десятиразрядным двоичным кодом (N=2n=10), когда количество возможных кодовых комбинаций равно Ш=2¹⁰=1024. Об этом свидетельствует шкала представления исходных и закодированных значений ТМП (Ш=0-1023). Такой формат представления наиболее часто используют в отечественной практике телеизмерений.

Значения телеизмерений были искажены на всем интервале представления данных шумовой помехой, из-за чего изображение ТМП отображается на фиг. 1 жирной линией, вызванной случайным шумом в младших разрядах позиционного двоичного кода. Кроме того, на отдельном временном участке от 1000 мсек до 4000 мсек передаваемый ТМП был дополнительно искажен импульсной помехой.

На фиг. 2 представлено графическое отображение того же ТМП, но после использования алгоритма ПСАП, приводящего к случаю безызбыточного помехоустойчивого кодирования, реализующего формулу структурно-алгоритмических преобразований (7).

На фиг. 3 представлены вычисленные значения инварианта, который принимает при отсутствии искажений телеизмерений помехами постоянное значение. С точки зрения математики он проявляется в виде группового свойства «равноостаточности», которое оказывается справедливым для отдельных графических фрагментов ТМП, заключенных между разрывами первого рода, идентифицированных, как δ_iM^*=|C_j^*-C_j+1^*| при δ_i^*>0,8×2^N, где C_j^*=C_j+ε_j, a ε_j - ошибка телеизмерений, обусловленная помехой; C_j - результат дополнительного безызбыточного помехоустойчивого кодирования j-того по принятому порядку счета слова-измерения или сообщения Xj; δ_jM^*=|C_j^*+C_j+1^*| и δ_(j+s)M^*=|C_(j+s)^*-C_(j+s)+1^*| - соседние максимальные значения абсолютных разностей между результатами дополнительного безызбыточного помехоустойчивого кодирования слов-измерений или сообщений, превышающие значение (0,8×2^N) и определяющие, с учетом искажений возможными ошибками ε_jM и ε_(j+s)M, начало и окончание графических фрагментов закодированных на основе перестановки составных частей или кодовых сегментов первоначальных значений телеметрируемых параметров; N- число разрядов, используемых для представления X_j и C_j.

Появление группового свойства «равноостаточности» связано с тем, что перестановка при дополнительном кодировании C_j, предполагающем

перестановку местами старших и младших полуслов a_2j и a₁j исходных значений телеизмерений X_j, j=0, 1, 2 … в соответствии с формулой (7) соответствует из-за сохранения позиционной структуры сформированного в результате дополнительного кодирования значений C_j умножению X_j на соответствующий модуль сравнения m₃, равный для случая перестановки младших и старших полуслов значению m₃=2ⁿ. Однако это свойство выполняется только в пределах выделенного графического фрагмента, заключенного между разрывами, определяемыми вычисленными значениями δ_jM^*=|C_j^*+C_j+1^*| и δ_(j+s)M^*=|C_(j+s)^*-C_(j+s)+1^*|.

Следовательно, если в выделенных при приеме ТМИ графических фрагментах преобразованного ТМП результаты кодирования C_j, которые не искажены помехой ε_j, и разделить на модуль сравнения m₃, равный минимальному кодовому расстоянию d_min, то получим одни и те же остатки от деления C_j на m₃. Для наглядности на фиг. 2 и фиг. 3 пример выделения графических фрагментов преобразованного ТМП отображен вертикальными линиями. Из приведенного на фиг. 3 графика следует, что значения остатков от деления находятся в узком диапазоне данных при отсутствии искажений импульсной помехой. Мода закона их распределений четко выражена и представляет собой значение кандидата-инварианта. Поэтому шумовые ошибки телеизмерений обнаруживают и исправляют с высокой вероятностью (до значений Р_и=0,99). Об этом свидетельствует и более тонкая линия графического представления восстановленного при приеме ТМП (фиг. 4), поскольку был исправлен шум, обусловленный искажениями младших разрядов двоичного кода. Наиболее сложный случай для обнаружения и исправления ошибок телеизмерений проявляется при искажении мощной импульсной помехой. Он промоделирован на временном интервале от 1000 мсек до 4000 мсек (фиг. 1-4). В этом случае закон распределения значений «равноостаточности» имеет не одну, а несколько вершин. При этом задача идентификации кандидата-инварианта заключается в

том, чтобы выбрать максимальное значение «равноостаточности», принадлежащее одной из наблюдаемых вершин закона распределения значений «равноостаточности». Однако при этом могут оставаться неисправленные ошибки ε^/_j (на фиг. 4 их три). Особенность инварианта в виде свойства «равноостаточности» также проявляется в том, что его значения одновременно можно рассматривать и как номер (μ) «узких» шкал телеизмерений, к которым относятся выделенные фрагменты (фиг. 3). Из графического представления, приведенного на фиг. 3, следует, что μ принимает значения от 0 до 31. При этом число разрешенных позиций безызбыточного кода в выделенных графических фрагментах ТМП равно μ=32. В итоге получаем те же m₃×μ=32×32=1024 значений 10-тиразрядных конструкций двоичного кода, что и при исходном традиционном графическом отображении передаваемого ТМП для случая десятиразрядных двоичных слов-измерений (Ш=(0-1023)).

Из сравнения иллюстраций, приведенных на фиг. 1-4, следует:

1) минимальное кодовое расстояние увеличено в 2ⁿ раз, что пр