Способ временной синхронизации системы связи на основе ортогонального частотного разделения каналов с мультиплексированием по преамбуле

Способ временной синхронизации системы связи на основе ортогонального частотного разделения каналов с мультиплексированием по преамбуле

Иллюстрации

Показать все

Реферат

Изобретение относится к области радиотехники, в частности к способу временной синхронизации системы связи. Технический результат - повышение помехоустойчивости временной синхронизации системы связи.

В последние годы к каналам связи на основе ортогонального частотного разделения каналов с мультиплексированием - OFDM (англ. Orthogonal Frequency-Division Multiplexing) проявляется повышенное внимание. На основе этой технологии функционируют следующие стандарты связи: WiFi, WiMAX, LTE. Главным достоинством технологии OFDM является ее высокая устойчивость к межсимвольной интерференции за счет введения циклического префикса. Для функционирования этой технологии необходимо, чтобы приемник синхронизировался по преамбуле и также по преамбуле рассчитал массив обратных комплексных коэффициентов передачи для используемых спектральных компонент, который будет применяться для комплексного умножения на спектр каждого последующего символа, с целью коррекции комплексной передаточной характеристики канала связи (англ. linear equalization).

В системах связи, в том числе с подвижными объектами, каналы распространения сигнала между приемником и передатчиком данных являются многолучевыми и нестационарными. Эффективность систем связи во многом определяется способностью алгоритмов временной синхронизации обеспечить в многолучевых нестационарных каналах необходимую точность оценки временного положения сигнала.

Для временной синхронизации обычно используют специальный сигнал - преамбулу, которая предшествует информационному сообщению. Преамбула представляет собой символ или символы OFDM с заранее известным спектральным составом.

OFDM сигнал представляет собой последовательность OFDM символов. Каждый такой символ состоит из двух частей - циклического префикса и многочастотного информационного символа. Многочастотный информационный символ представляет собой сумму модулированных гармоник. Под циклическим префиксом понимают некоторую последовательность отсчетов сигнала, которая непосредственно предшествует каждому многочастотному информационному символу и представляет собой конечную часть этого символа. Как правило, длительность префикса меньше длительности информационного символа. Наличие циклического префикса позволяет уменьшить или полностью устранить межсимвольную интерференцию (IEEE Std 802.11а - 1999, Прокис Дж., Цифровая связь. Перевод с английского. М.: Радио и связь, 2000, с. 593).

Пример получения OFDM символа преамбулы описан ниже и представлен на фиг. 1. В основе подхода лежит преобразование Фурье, а точнее алгоритм быстрого преобразования Фурье. Создается спектр сигнала, из которого обратным быстрым преобразованием Фурье получается временное представление сигнала, далее путем копирования конечной части символа и переноса ее в начало (такое копирование позволяет избежать разрыва в месте «склейки» префикса) получается циклический префикс длительностью N_g дискрет (отсчетов по времени). Общая длительность символа в дискретах составляет N_S=N+N_g. Для размерности преобразования Фурье, равной N, количество используемых спектральных компонент должно быть меньше N-1, как минимум не используются компоненты 0 и N/2. Может быть не использовано и большее количество спектральных компонент, так для фиг. 1 количество используемых компонент равно 4z и меньше N-1.

Известен способ временной синхронизации, описанный в патенте США №5,732,113 от 24.03.1998, авторов: Schmidl Т.М., Сох D.C., Timing and Frequency Synchronization of OFDM signals. В упомянутом патенте предложен способ (метод Шмидл и Кокс) синхронизации параметров сигнала в OFDM системах, который основан на приеме преамбулы. Первый символ преамбулы, по которому осуществляется временная синхронизация, включает каждую 2-ую спектральную компоненту, т.е. данный символ во временной области состоит из двух идентичных частей и циклического префикса. В процессе синхронизации временное положение сигнала определяют по положению максимума решающей функции:

где

N - количество точек в преобразовании Фурье;

d - временной индекс, соответствующий первому дискрету в окне из N дискрет;

r - комплексное значение оцифрованного принятого сигнала.

Главным недостатком метода является плоская вершина решающей функции (1), которая при наличии шумов приводит к значительным ошибкам временной синхронизации. Временная метрика решающей функции без шумов и искажений для метода Шмидл и Кокс представлена на фиг. 2 (сплошная линия).

Также известен способ временной синхронизации, описанный в статье Minn Н., Zeng М., Bhargava V.K., On Timing Offset Estimation for OFDM Systems // IEEE COMMUNCATIONS LETTERS, VOL. 4, NO. 7, JULY 2000, pp. 242-244. В указанной статье предложено два различных усовершенствования аналога (метода Шмидл и Кокс): метод А и метод В. Метод А так же, как метод Шмидла и Кокса, основан на обработке символа преамбулы, состоящей во временной области из двух идентичных частей и циклического префикса.

В методе А дополнительно используется свойство обязательного наличия циклического префикса длительностью N_g в OFDM символе. Оценку временной задержки входного сигнала определяют по положению максимума решающей функции (2). Временная метрика без шумов и искажений для метода А представлена на фиг. 2 пунктирной линией.

Решающая функция имеет вид:

где N_g - длительность циклического префикса в дискретах;

N - количество точек в преобразовании Фурье;

d - временной индекс;

r - комплексное значение оцифрованного принятого сигнала.

Наиболее близким по технической сущности к заявленному методу является выбранный в качестве прототипа способ определения временного сдвига (метод В), описанный в статье Minn Н., Zeng М., Bhargava V.K., On Timing Offset Estimation for OFDM Systems // IEEE COMMUNCATIONS LETTERS, VOL. 4, NO. 7, JULY 2000, pp. 242-244.

Временная синхронизация системы связи методом В заключается в следующем:

на передающей стороне формируют преамбулу из OFDM символов, модулированных по схеме квадратурной фазовой манипуляции, содержащих циклический префикс, первый символ которой используют для определения по нему временного положения сигнала; сигнал преамбулы переносят на несущую частоту; усиливают и передают его по каналу связи;

на приемной стороне входной сигнал фильтруют, усиливают, переносят на нулевую промежуточную частоту, осуществляют его аналого-цифровое преобразование, формируя входной цифровой комплексный сигнал на нулевой промежуточной частоте;

далее формируют решающую функцию (см. временную метрику без шумов и искажений для метода В на фиг. 2 - штриховая линия), определяемую формулой (4);

определяют максимум М решающей функции M₂(d) и по его положению оценивают временную задержку сигнала;

первый символ преамбулы, используемый для определения по нему временного положения сигнала, состоит из четырех одинаковых по длине частей, первые две из которых идентичны, а последние две негативны по отношению к первым двум.

где

L=N/4;

N- количество точек в преобразовании Фурье;

d - временной индекс;

r - комплексное значение оцифрованного принятого сигнала.

На фиг. 3 представлена зависимость дисперсии оценки временного положения сигнала от отношения сигнал/шум для метода Шмидл и Кокс, метода Шмидл и Кокс с использованием формулы (3), метода А, метода В и метода В с использованием формулы (3). Наименьшее значение дисперсии наблюдается у метода В.

Недостатком выбранного прототипа является низкая точность при значительных шумах, которая обусловлена применением решающей функции с относительно плоским максимумом.

Задачей предлагаемого изобретения является повышение помехоустойчивости временной синхронизации системы связи.

Поставленная задача решается за счет того, что решающая функция представляет собой квадрат модуля комплексной функции взаимной корреляции принятого сигнала и символа эталонной преамбулы без циклического префикса, который не передавался через канал передачи, а был заранее известен. Символ преамбулы представляет собой дельта-коррелированный шумоподобный сигнал. Использование именно этого свойства при обработке приводит к повышению точности за счет резкого сужения области максимума решающей функции.

Необходимо отметить, что преамбула для предлагаемого способа может содержать один, два или более двух символов, каждый из которых во временной области не имеет повторяющихся участков. Это необходимо, чтобы максимум решающей функции был один для каждого символа, который используется для синхронизации.

Использование преамбулы, состоящей из двух символов, с разделением спектра, как на фиг. 4, дает возможность исключить процедуру аппроксимации, используемую для определения массива обратных комплексных коэффициентов передачи в стандартной методике реализации системы связи OFDM, которая предполагает наличие в символе преамбулы не всех спектральных компонент (IEEE DRAFT Standard for Local and metropolitan area networks P802.16Rev2/D7 October 2008, Part 16: Air interface for fixed and mobile broadband wireless access systems. Chapter 8.3.3.6 Preamble structure and modulation, pp. 646-647), так как имеется полный набор спектральных компонент, по которым рассчитывают массив обратных комплексных коэффициентов передачи, применяемый для комплексного умножения на спектр каждого последующего символа с данными, с целью компенсации влияния канала связи на символ данных для исключения ошибок при его демодуляции (англ. linear equalization), а также появляется дополнительная возможность использовать второй символ преамбулы для временной синхронизации, по аналогии с первым, что дополнительно позволяет повысить помехоустойчивость. Каждый из символов преамбулы при разделении спектра как показано на фиг. 4 не имеет повторяющихся участков.

Краткое описание чертежей.

На фиг. 1 показан условный амплитудный спектр OFDM символа, а также представлен OFDM символ во временной области, где обозначено:

N - количество точек в преобразовании Фурье;

4z - количество используемых спектральных компонент;

N_g - длительность циклического префикса;

Ns - общая длительность OFDM символа, N_S=N_g+N.

На фиг. 2 показана временная метрика решающих функций без шумов и искажений для метода Шмидл и Кокс, метода А и метода В. Ширина решающей функции для прототипа (метод В) на уровне 0.1 составляет Δ_B≈200 дискрет.

На фиг. 3 представлены зависимости дисперсии оценки временного положения сигнала от отношения сигнал/шум для методов Шмидл и Кокс, метода А и метода В, а также метода Шмидл и Кокс и метода В с использованием в расчетах формулы (3).

На фиг. 4 изображен условный амплитудный спектр преамбулы из двух символов, включающий весь набор спектральных компонент, необходимый для расчета массива значений обратных комплексных коэффициентов передачи.

На фиг. 5 изображена нормированная решающая функция предлагаемого способа без шумов, начало преамбулы в точке с индексом по времени 511.

На фиг. 6 и фиг. 7 представлена нормированная решающая функция предлагаемого способа без шумов, начало преамбулы в точке с индексом, равным N_g/2. Ширина решающей функции для предлагаемого способа на уровне 0.1 составляет Δ_C≈4 дискрета, что приблизительно в 50 раз меньше, чем у прототипа.

На фиг. 8 показан первый символ преамбулы во временной области, состоящий из 1126 отсчетов по времени, т.е. N_S=N+N_g=1024+102=1126.

На фиг. 9 и фиг. 10 представлена временная метрика нормированной решающей функции при прохождении сигнала преамбулы по реальному каналу связи, имеющему неравномерность группового времени запаздывания, что приводит к расширению области максимума решающей функции. На фиг. 10 обозначены индексы по времени a и b, соответствующие границам диапазона значимости решающей функции.

На фиг. 11 показаны результаты моделирования зависимости дисперсии оценки временного положения сигнала от отношения сигнал/шум для предложенного способа временной синхронизации и канала с аддитивным белым Гауссовым шумом. Каждая точка на графике построена с шагом в 1 дБ по 100000 реализациям сигнала совместно с аддитивным белым Гауссовым шумом (АБГШ).

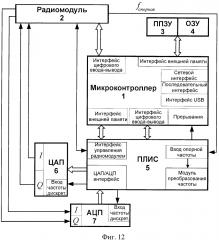
На фиг. 12 изображена блок-схема цифрового модема, в котором может быть реализован предложенный способ временной синхронизации.

Для проведения временной синхронизации на основе комплексной функции взаимной корреляции между принятым сигналом и символом эталонной преамбулы без циклического префикса, рассчитываемой через обратное преобразование Фурье от произведения спектра принятого сигнала на комплексно сопряженный спектр соответствующего символа эталонной преамбулы, формируется решающая функция (5) (см. нормированную решающую функцию без шумов на фиг. 5-7):

где IFFT - обратное преобразование Фурье;

FFT - прямое преобразование Фурье;

r[d] -массив данных принятого сигнала, состоящий из N временных отсчетов;

N - количество точек в преобразовании Фурье;

Р_Э^*[f] - массив комплексно сопряженных спектральных компонент символа эталонной преамбулы, т.е. преамбулы, которая не передавалась через канал передачи, а была заранее известна;

d - временной индекс для массивов r[d] и M_K[d].

В реальном канале связи время запаздывания зависит от частоты, т.е. имеется неравномерность группового времени запаздывания (ГВЗ), которая приводит к «растеканию» максимума решающей функции (см. нормированную решающую функцию при прохождении сигнала преамбулы по реальному каналу связи на фиг. 9-10). Что приводит к затруднению при установке порогового коэффициента k для обнаружения преамбулы таким образом, чтобы не было ложных обнаружений и пропусков. Для устранения этого недостатка предлагается использовать сумму значений M_S решающей функции на участке значимости, т.е. в диапазоне индекса от а до b, вместо значения максимума решающей функции (см. фиг. 10).

Таким образом, основной критерий обнаружения преамбулы при растекании максимума решающей функции:

M_S>k⋅А,

где k - порог обнаружения;

- среднее значение решающей функции, рассчитываемое в диапазоне индекса d от 0 до N-1, исключая из этого интервала диапазон индекса d от а до b.

Значение M_S рассчитывается на участке значимости как сумма значений решающей функции в диапазоне индекса d от а до b:

где а - это первый индекс, когда значение решающей функции больше отношения максимума решающей функции М к Q;

b - последний индекс, когда значение решающей функции больше отношения максимума решающей функции М к Q.

Для снижения вероятности ложного обнаружения условие M_S>k⋅A целесообразно дополнить двумя условиями: I<N-N/4 и b-a<N_g,

где I - индекс, соответствующий временному положению максимума решающей функции M_K[d], т.е. М=M_K[I].

Условие I<N-N/4 не позволяет определять наличие преамбулы, если она найдена на отрезке решающей функции от N-N/4 до N-1. Применимость этого условия обусловлена тем, что на следующем шаге подстройки (переменная step=N/2 в алгоритме обнаружения) произойдет обнаружение преамбулы в лучших условиях, т.к. большее количество дискрет преамбулы (большее на step дискрет) попадет в массив данных принятого сигнала r[d]. Если I≥N-N/4, то это означает, что в массив данных принятого сигнала r[d] попало не более чем N/4+N_g дискрет (временных отсчетов) преамбулы.

Условие b-a<N_g говорит о том, что «растекание» решающей функции на выбранном уровне значимости не может быть больше длины циклического префикса, другими словами ширина участка значимости должна быть меньше длины циклического префикса.

Значение порогового коэффициента k зависит от количества используемых компонент преамбулы и длительности циклического префикса N_g. Для исключения ошибок временной синхронизации необходимо, чтобы значение коэффициента k было больше, чем отношение M_S/A для дискретизированного сигнала преамбулы без шумов, при попадании в массив данных принятого сигнала только циклического префикса преамбулы, т.е. в массив r[d] попадает N_g дискрет символа преамбулы. Такая установка порогового коэффициента гарантирует, что преамбула не будет определена при попадании в массив r[d] только циклического префикса, если бы произошло такое определение, то временной индекс положения преамбулы I был бы ошибочно определен на отрезке от 0 до N_g-1, реальный индекс максимума в этом случае позже на N дискрет, т.е. правильное временное положение преамбулы начинается в индексе времени I+N. При увеличении длины циклического префикса и попадании в массив r[d] только циклического префикса отношение M_S/A также увеличивается, поэтому значение коэффициента k должно быть соответственным образом увеличено.

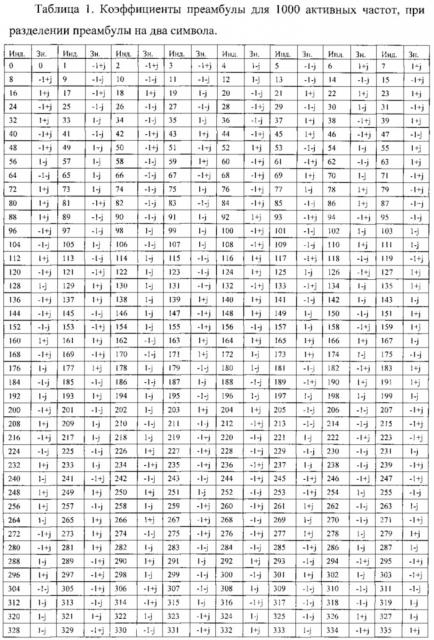
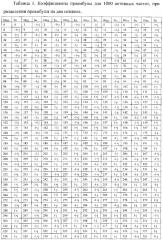
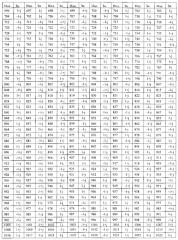
Для сравнения прототипа и предлагаемого способа в одинаковых условиях будем рассматривать преамбулу, содержащую два символа данных, каждый из которых содержит число компонент, равное половине используемых спектральных компонент (в прототипе используется 1000), модулированных по схеме квадратурной фазовой манипуляции (QPSK). Амплитудный спектр преамбулы представлен на фиг. 4. Количество спектральных компонент в одном символе равно 2z, и для соответствия прототипу 2z=500. Количество точек в преобразовании Фурье N=1024, длительность циклического префикса N_g=102. Для моделирования предлагаемого способа использовались спектральные компоненты, представленные в таблице 1, и первый символ преамбулы. При выбранных параметрах значение порогового коэффициента k>101 (получено по результатам моделирования при расчете отношения M_S/А при попадании в массив r[d] N_g дискрет циклического префикса преамбулы без шумов). Для дальнейшего моделирования выберем k=200.

Способ реализуется следующим образом.

Принятый сигнал с выхода радиомодуля заданного уровня с нулевой промежуточной частотой оцифровывается АЦП, получается массив входных комплексных данных r[i]. Обработка данного массива осуществляется представленным ниже алгоритмом.

Алгоритм обнаружения преамбулы.

Особенностью алгоритма является синхронизация в точку с индексом по времени N_g/2, соответствующую середине циклического префикса. При такой синхронизации обеспечивается наименьшее возможное наложение OFDM символов друг на друга, т.е. минимизируется межсимвольная интерференция.

1. Инициализация переменных: состояние state=0, сдвиг shift=0.

2. Рассчитывается решающая функция (5) в диапазоне от shift до shift+N-1 дискрет. Решающая функция является квадратом модуля комплексной функции взаимной корреляции между принятым сигналом и заранее известным символом эталонной преамбулы без циклического префикса, которая определяется как обратное преобразование Фурье от комплексного произведения спектра принятого сигнала на комплексно сопряженный спектр символа эталонной преамбулы Р_Э^*[f] (формула (5)). При этом спектр символа эталонной преамбулы известен заранее, а спектр принятого сигнала получается после прямого преобразования Фурье от временной области принятого сигнала. Значение переменной shift должно лежать в диапазоне возможных значений оцифрованного АЦП массива данных, т.е. если значение shift+N-1 больше максимального оцифрованного индекса в массиве r[i], то переход к концу алгоритма с результатом: преамбула не обнаружена. Более подробно расчет решающей функции M_K[d] описан в пп. 2.1-2.7.

2.1. Определяется комплексный спектр принятого сигнала через прямое преобразование Фурье r_f[f]=FFT(r[d]),

где f=0, 1, 2, … N-1 - индекс частоты в спектре;

d=0, 1, 2, …, N-1 - индекс отсчета по времени в полученном массиве данных после сдвига на shift дискрет относительно начала;

N - количество точек в преобразовании Фурье.

2.2. Устанавливается индекс частоты f=0.

2.3. Если f<N, то переход к п. 2.4, иначе к 2.6.

2.4. Определяется комплексная точка в массиве S[f]=r_f[f]⋅Р_Э^*[f].

2.5. Инкрементирование индекса частоты f=f+1. Переход к п. 2.3.

2.6. Определяется массив комплексной функций взаимной корреляции через обратное преобразование Фурье corr[d]=IFFT(S[f]).

2.7. Рассчитывается массив решающей функции как квадрат модуля от массива corr[d].

M_K[d]=corr_Re[d]⋅corr_Re[d]+corr_Im[d]⋅corr_Im[d],

где d=0, 1, 2, …, N-1;

corr_Re[d], corr_Im[d] действительные и мнимые части комплексного массива corr[d] соответственно.

3. Определяется максимум М решающей функции M_K[d] и индекс, соответствующий данному максимуму - I, т.е. М=M_K[I].

4. Определяется значение переменной M_Q:M_Q=M/Q.

5. Поиск индекса а, где а - это первый индекс, когда значение решающей функции больше отношения максимума М к Q. Поиск индекса осуществляется путем перебора индекса d от 0 до I: если M_K[d]>M_Q, тогда a=d.

6. Поиск индекса b, где b - это последний индекс, когда значение решающей функции больше отношения максимума М к Q. Поиск индекса осуществляется путем перебора индекса d от N-1 до I: если M_K[d]>M_Q, тогда b=d.

7. Рассчитывается сумма значений функции M_K[d] на участке значимости, т.е. в интервале индекса d от а до b:

8. Рассчитывается среднее значение А решающей функции в интервалах от 0 до а-1 и от b+1 до N-1:

- среднее значение решающей функции, рассчитанное при исключении участка значимости.

9. Если state=0 (преамбула ни разу не обнаруживалась), то переход к шагу 10, иначе к шагу 13.

10. Если M_S>k⋅A, I<N-N/4 и b-a<N_g, то переход к шагу 11, иначе к шагу 12, где k - порог обнаружения. Выполнение условий означает, что преамбула найдена, и необходимо установить сдвиг по времени таким образом, чтобы максимум функции был в середине циклического префикса (шаг 11). Иначе, сдвиг в плюс по времени на step дискрет (шаг 12) и еще одна попытка обнаружить преамбулу первый раз.

11. shift=shift+I-N_g/2, state=1, переход к шагу 2. Настройка сдвига по времени таким образом, чтобы максимум функции был в середине циклического префикса.

12. shift=shift+step - сдвиг времени на step дискрет. Переход к шагу 2.

13. Если M_S>k⋅A, I<N-N/4 и b-a<N_g, то переход к шагу 14, иначе к шагу 15.

14. shift=shift+I-N_g/2. Преамбула обнаружена. Переход к шагу 16.

15. Преамбула не обнаружена.

16. Конец.

Выбор порогового уровня M_Q в 25% (Q=4) относительно максимума позволяет легко реализовывать его расчет в аппаратуре за счет деления максимального значения М на 4 с использованием битового сдвига вправо на 2.

Для уменьшения количества итераций поиска преамбулы рекомендуется установить значение переменной step=N/2.

Для улучшения помехоустойчивости алгоритма значение переменной step должно быть уменьшено, минимальное значение равно 1.

При реализации алгоритма в аппаратуре для непрерывного поиска преамбулы во время работы алгоритма входной массив r[i] непрерывно заполняется новыми значениями, оцифрованными АЦП. В случае если необходимое количество точек для следующей итерации еще не оцифровано, то делается задержка выполнения алгоритма обнаружения преамбулы до момента времени, пока необходимое количество данных не будет собранно.

Условия моделирования алгоритма обнаружения преамбулы представлены ниже.

Спектральные компоненты преамбулы, состоящей из двух символов, представлены в таблице 1. Индексы частот, используемые в преобразовании Фурье, представлены в столбце с названием «Инд.», значения спектральных компонент представлены в столбце с названием «Зн.». Временное представление сигнала для реальной и мнимой части первого символа, по которому осуществлялось моделирование, представлено на фиг. 8. Количество спектральных составляющих в первом символе преамбулы, по которому осуществлялась синхронизация, равно 500, т.е. для фиг. 4 2z=500. Первый символ содержит спектральные составляющие с индексами от 1 до 250 и от 774 до 1023. Параметр шага step=N/2=512. Канал с аддитивным белым Гауссовым шумом (АБГШ), время запаздывания одинаково для всех частот.

При step=N/2 преамбула, соответственно, должна быть обнаружена на интервале, не меньшем чем от 0 до N/2-1. На фиг. 5 показано обнаружение преамбулы с индексом максимума на 511-ой точке (первая точка в массиве 0-вая), т.е. в массив r[d] попало 512+N_g=614 дискрет преамбулы. При таком захвате преамбулы для сигнала без шумов отношение M_S/A≈1115. Для АБГШ канала с отношением сигнал/шум 3 дБ и тех же условий M_S/A≈350.

На фиг. 7-8 показано обнаружение преамбулы с индексом максимума на 51-ом дискрете (середина циклического префикса) при полном попадании преамбулы в массив r[d], для сигнала без шумов отношение M_S/A≈9217.

Расчетное значение M_S/А при полном попадании преамбулы в массив r[d] для моделирования АБГШ канала с отношением сигнал/шум 20 дБ равно 8690, расчетное значение M_S/A для реальной линии связи со значительной неравномерностью группового времени запаздывания (фиг. 9) M_S/А≈8501 (результаты эксперимента). Т.о. отношение M_S/A слабо зависит от неравномерности группового времени запаздывания. При выбранном пороговом значении k=200 будет происходить верное обнаружение преамбулы (без ложных обнаружений и пропусков) вплоть до отношения сигнал/шум 3 дБ, при параметре step=N/2=512.

Для сравнения, если вместо суммы значений M_S решающей функции на участке значимости использовать максимум решающей функции, то при тех же условиях отношение М/А≈499 для моделирования АБГШ канала с отношением сигнал/шум 20 дБ и М/А≈99 для реальной линии связи со значительной неравномерностью группового времени запаздывания. Пятикратная разница в значениях не позволит задать пороговый коэффициент для обнаружения преамбулы так, чтобы не было ложных обнаружений и пропусков.

В результате выполнения алгоритма обнаружения преамбулы с результатом «преамбула обнаружена» идеальное значение индекса I=N_g/2, однако, из-за шумов и неравномерности ГВЗ может происходить допустимое отклонение от N_g/2, например ±N_g/10. Т.о., если N_g/2+N_g/10≥I≥N_g/2-N_g/10, то синхронизация считается успешной и возможна дальнейшая обработка OFDM символов, иначе переходят в алгоритм обнаружения преамбулы.

Алгоритм поддержания временной синхронизации.

Алгоритм основывается на начальной синхронизации через алгоритм обнаружения, постоянной длительности фрейма (как правило, составляющей несколько сотен символов) и небольшом расхождении между опорными частотами передающего и приемного модемов (как правило, не хуже 10^-6). Например, при длительности фрейма 100 символов и длительности одного символа 1126 дискрет имеем изменение индекса положения максимума на 0,1 дискрет (100*1126*10^-6≈0,1 дискрет). Эти моменты обуславливают, что от фрейма к фрейму индекс положения максимума решающей функции без дополнительной подстройки меняется меньше, чем длительность циклического префикса (в условиях реального радиоканала меняется не более чем на несколько дискрет, резкие изменения обусловлены неравномерностью ГВЗ, при отсутствии резких изменений канала из-за несовпадения опорных частот возможно изменение на 1 дискрет). Т.о., принимая преамбулу следующего фрейма, можно с уверенностью сказать, что максимум решающей функции лежит относительно предыдущего своего местоположения в диапазоне плюс минус половины длительности циклического префикса. Все эти свойства упрощают алгоритм поддержания синхронизации. По шагам алгоритм может быть представлен:

1. shift=0.

Пункты 2-8 идентичны соответствующим пунктам алгоритма обнаружения преамбулы.

9. Если MS>k⋅A, I<N_g и b-a<N_g, то преамбула обнаружена - переход к пункту 10, иначе переход в алгоритм обнаружения преамбулы.

10. Δ=I-N_g/2.

Для поддержания синхронизации текущий фрейм должен быть удлинен на Δ дискрет, за счет изменения защитного интервала, который находится в конце фрейма, это приведет к тому, что следующий фрейм будет принят позже на Δ дискрет и индекс положения максимума уменьшится на Δ дискрет.

Результаты моделирования представленных алгоритмов при параметре step=1 для спектральных компонент преамбулы, представленных в таблице 1, и АБГШ канала представлены на фиг. 11. Каждая точка графика получена по 100000 реализациям сигнала и шума.

Зависимость дисперсии оценки временного положения сигнала от отношения сигнал/шум для предложенного метода показывает, что точность временной синхронизации значительно увеличилась. Наименьшая дисперсия оценки для прототипа и АБГШ канала составляет приблизительно 0,8 дискрет² (Minn Н., Zeng М., Bhargava V.K., On Timing Offset Estimation for OFDM Systems // IEEE COMMUNCATIONS LETTERS, VOL. 4, NO. 7, JULY 2000, pp. 242-244) при отношении сигнал/шум 0 дБ (см. фиг. 3), тогда как в предложенном способе синхронизации даже при отношении сигнал/шум -12 дБ дисперсия составляет 0,046, а при отношении сигнал/шум 0 дБ - дисперсия равна 0 (см. фиг. 11), т.е. полностью отсутствуют неправильные определения временного положения преамбулы. Выигрыш по сравнению с прототипом составляет более 12 дБ.

Способ может использовать один или несколько символов преамбулы. При работе по двум символам, представленный выше алгоритм выполняется дважды, при этом дополнительно возникает возможность усреднить результаты и сделать выводы о неравномерности ГВЗ по значениям индексов а и b в зависимости от номера символа преамбулы.

Способ может быть реализован в устройстве DMT модема (англ. Discrete multitone modulation - дискретная многотональная модуляция) или OFDM модема, типовая блок-схема которого представлена на фиг. 12, а также в любом другом устройстве, которое позволит реализовать представленный выше алгоритм работы. Модули расчета прямого и обратного преобразований Фурье обязательно присутствуют во всех OFDM и DMT модемах, что упрощает аппаратную реализацию предлагаемого способа.

Способ был апробирован в реальных условиях радиоканала на основе OFDM модема (см. Фиг 12). На фиг. 12 обозначены: микроконтроллер 1, радиомодуль 2, программируемое постоянное запоминающее устройство (ППЗУ) 3, оперативное запоминающее устройство (ОЗУ) 4, программируемая логическая интегральная схема (ПЛИС) 5, цифро-аналоговый преобразователь (ЦАП) 6, аналого-цифровой преобразователь (АЦП) 7.

Опорная частота f_{опорная} преобразуется в ПЛИС в модуле преобразования частоты на основе ФАПЧ в тактовую частоту работы ПЛИС, частоту дискретизации ЦАП и частоту дискретизации АЦП. Опорная частота изменяется в небольших пределах за счет управляющего воздействия с микроконтроллера. Микроконтроллер взаимодействует с ПЛИС и интерфейсами ввода-вывода (интерфейс USB, сетевой интерфейс, последовательный интерфейс) через прямой доступ в память и соответствующие прерывания. Микроконтроллер подключен к энергонезависимой памяти ППЗУ и оперативной памяти ОЗУ через интерфейс памяти, что позволяет создавать ресурсоемкие алгоритмы обработки и управления. В задачи микроконтроллера входит управление режимами работы ПЛИС и радиомодуля, а также высокоуровневая обработка данных. В ПЛИС реализуются критические по скорости процедуры, такие как прямое и обратное преобразования Фурье, помехоустойчивое кодирование, шифрование.

Кратко алгоритм работы передатчика цифрового модема можно представить так: передаваемая информация поступает на порт сетевого интерфейса, данные шифруются, рандомизируются, кодируются (вносится избыточность), перемешиваются, модулируются, с использованием обратного преобразования Фурье создаются OFDM символы, которые подаются на вход ЦАП, выход которого соединен с входом радиомодуля. ЦАП генерирует OFDM сигнал с нулевой промежуточной частотой, поэтому задача радиомодуля перенести спектр сигнала с выхода ЦАП на заданную несущую частоту.

Краткий алгоритм работы приемника цифрового модема можно описать следующим образом. Выходной сигнал заданного уровня с нулевой промежуточной частотой с выхода радиомодуля оцифровывается АЦП. По преамбуле, оцифрованной АЦП, производится временная синхронизация и рассчитывается массив значений обратного комплексного коэффициента передачи,

где f_S - частота дискретизации;

N - количество точек в массиве данных преобразования Фурье;

U_PRE - массив заранее известных спектральных составляющих эталонной преамбулы;

U_RCV - массив спектральных составляющих преамбулы, прошедших через канал передачи;

i - целое число от 1 до 2z и от N-2z до N-1;

4z - количество используемых компонент.

Все последующие спектры OFDM символов данных умножаются на соответствующий коэффициент из массива K_inverse[if_s/N], далее данные демодулируются, деперемешиваются, декодируются, дерандомизируются и дешифрируются и передаются на выход через сетевой интерфейс.

Наибольший эффект от использования предложенного способа может быть достигнут в цифровых средствах связи реализованных по технологии OFDM и DMT. Предлагаемый способ существенно повышает помехоустойчивость временной синхронизации системы связи и расширяет область ее применимости.

Способ временной синхронизации системы связи, заключающийся в том, что на передающей стороне формируют преамбулу из OFDM символов, модулированных по схеме квадратурной фазовой манипуляции, содержащих циклический префикс, первый символ которой используют для определения по нему временного положения сигнала; сигнал преамбулы переносят на несущую частоту; усиливают и передают его по каналу связи; на приемной стороне входной сигнал фильтруют, усиливают, переносят на нулевую промежуточную частоту, осуществляют его аналого-цифровое преобразование, формируя входной цифровой комплексный сигнал на нулевой промежуточной частоте; далее формируют решающую функцию и определяют ее максимум и по индексу положения максимума оценивают временную задержку сигнала, отличающийся тем, что формируют символ преамбулы, не имеющий повторяющихся участков во временной области, кроме циклического префикса; рассчитывают решающую функцию как квадрат модуля комплексной функции взаимной корреляции между принятым сигналом и заранее известным символом эталонной преамбулы без циклического префикса; определяют участок значимости так, чтобы значение решающей функции на границах диапазона значимости было больше заданного уровня по отношению к максимуму решающей функции, участок значимости обязательно включает индекс положения максимума, а решающая функция за пределами участка значимости не имеет значений больше заданного уровня по отношению к максимуму решающей функции; рассчитывают сумму значений решающей функции на участке значимости; рассчитывают среднее значение решающей функции на всем ее протяжении за исключением участка значимости; используют основной критерий обнаружения преамбулы, заключающийся в том, что сумма значений решающей функции на участке значимости должна превышать произведение установленного порогового коэффициента на среднее значение решающей функции, рассчитанное при исключении участка значимости.