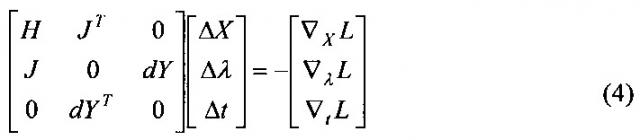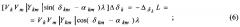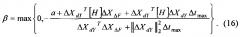Автоматизированное устройство определения предельных режимов электрических систем

Автоматизированное устройство определения предельных режимов электрических систем

Иллюстрации

Показать все

Реферат

Изобретение относится к информационно-измерительной и вычислительной технике и может быть использовано для оценки пределов статической устойчивости и определения границы существования режимов, то есть предельных режимов (ПР) электрических систем на основе их расчета в заданном направлении изменения мощностей.

Оценка ПР играет ключевую роль в анализе, планировании и управлении электрическими системами, поскольку определяет такой статически устойчивый установившийся режим, в котором произвольное малое изменение любого текущего параметра в неблагоприятном направлении вызывает коллапс напряжений или потерю синхронизма в системе.

Известно устройство для регистрации параметров переходных процессов изменения напряжения и тока в электрических сетях при авариях [RU 2376625, C1, G06F 17/40, H02J 3/00, 20.12.2009], содержащее группу аналоговых датчиков, группу цифровых датчиков, многоканальные первый аналоговый и второй цифровой коммутаторы, формирователь модуля, нуль-орган, источник опорных напряжений, дешифратор, первое, второе и третье оперативные запоминающие устройства, постоянное запоминающее устройство, микроконтроллер, таймер, первый-четвертый одноканальные аналоговые коммутаторы, аналого-цифровой преобразователь, первый и второй аналоговые компараторы, регистр, первый-пятый счетчики, первый-третий триггеры, элемент И-НЕ, первый-пятый элементы И, первый-четвертый элементы ИЛИ, первый-шестнадцатый одновибраторы, числовой компаратор и генератор тактовых импульсов.

Недостатком устройства является относительно узкие функциональные возможности, т.к. оно позволяет произвести только регистрацию параметров переходных процессов изменения напряжения и тока в электрических сетях при авариях и не позволяет определить их предельные режимы работы.

Известно также устройство дистанционного контроля за параметрами тока и напряжения в высоковольтной части электроэнергетических систем, включая контроль за переходными процессами в этих системах [RU 2143165, C1, H02J 13/00, 20.12.1999], содержащее подключенный к высоковольтной сети высоковольтный измерительный модуль, включающий в себя магнитно-связанный с высоковольтной сетью пассивный преобразователь сетевого тока и/или электрически связанный с высоковольтной сетью пассивный преобразователь сетевого напряжения, причем высоковольтный измерительный модуль содержит блок вторичного электропитания, подключенные к блоку вторичного электропитания, магнитно-связанный с высоковольтной сетью низковольтный питающий трансформатор тока и/или электрически связанный с высоковольтной сетью и включенный в цепь пассивного преобразователя сетевого напряжения низковольтный питающий трансформатор напряжения с фильтрующим конденсатором, шунтирующим первичную обмотку, и параллельным ему демпфирующим резистором, активный преобразователь сигналов измерительной информации, соединенный с пассивным преобразователем сетевого тока и/или пассивным преобразователем сетевого напряжения и блоком вторичного электропитания и имеющий радиочастотный и/или оптический выходы для преобразованных сигналов измерительной информации, а пассивный преобразователь сетевого напряжения выполнен в виде последовательно соединенных высоковольтного опорного конденсатора и низковольтного плеча, причем все элементы высоковольтного измерительного модуля, кроме высоковольтного опорного конденсатора, помещены в электрический экран, соединенный с сетевым проводом через дроссель и параллельный ему демпфирующий резистор.

Недостатком устройства является относительно узкие функциональные возможности, т.к. оно позволяет осуществить дистанционный контроль за параметрами тока и напряжения в высоковольтной части электроэнергетических систем и не позволяет определить их предельные режимы.

Кроме того, известно устройство [RU 2402067, C1, G06F 17/40, 20.10.2010], содержащее группу аналоговых датчиков, группу цифровых датчиков, аналоговый и цифровой коммутаторы, первый-четвертый счетчики, группу оперативных запоминающих устройств, постоянное запоминающее устройство, микроконтроллер, таймер, регистр, аналого-цифровой преобразователь, генератор тактовых импульсов, D-триггеры, первый-четвертый одновибраторы.

Недостатком устройства является относительно узкие функциональные возможности, поскольку при регистрации параметров переходных процессов в системах электроснабжения оно не позволяет, в частности, определить и максимальные, и аварийно допустимые перетоки в опасных сечениях электроэнергетических систем. Это ограничивает применение систем для определения их предельных режимов.

Наиболее близкой по технической сущности к предложенной является система мониторинга запасов устойчивости электроэнергетической системы [RU 2013142113/08, A, G06F 17/40, H02J 3/00, публ. 27.03.2015], содержащая группу оперативных запоминающих устройств, группу цифровых датчиков, запоминающее устройство, блок сбора и обработки данных, входы которого соединены с выходами оперативных запоминающих устройств группы, блок оценки состояния электроэнергетической системы, входы которого соединены с выходом блока сбора и обработки данных и с выходами цифровых датчиков группы, являющимися датчиками системы телеизмерений, а также последовательно соединенные блок определения предельных режимов, вход которого соединен с выходом блока оценки состояния электроэнергетической системы, блок определения опасных сечений и блок определения максимально допустимых и аварийно допустимых перетоков, выход которого соединен с входом запоминающего устройства.

Недостатком устройства является относительно низкая оперативность, поскольку, как указано в описании работы известного устройства, критерием достижения ПР является сходимость итерационного процесса решения нелинейных уравнений установившегося режима. Однако глобальная сходимость алгоритмов является по своей природе вычислительно затратной, а большая продолжительность обработки является обычной платой за надежную сходимость алгоритмов. Это снижает быстродействие устройства.

Задача, на решение которой направлено предложенное изобретение, заключается в повышении быстродействия устройства при определении предельных режимов (ПР) электрических систем.

Требуемый технический результат заключается в повышении быстродействия устройства при определении предельных режимов (ПР) электрических систем.

Поставленная задача решается, а требуемый технический результат достигается тем, что в устройство, содержащее группу блоков оперативной памяти, блок сбора данных и блок памяти, а также блок оценки предельных режимов, согласно изобретению выходы блоков оперативной памяти группы соединены с входом блока сбора данных, выход которого соединен с входом блока оценки предельных режимов, выход которого соединен с входом блока памяти, а блок оценки предельных режимов выполнен в виде последовательно соединенных вычислителя вектора множителей Лагранжа, вход которого является входом блока оценки предельных режимов, вычислителя предельного приращения коэффициента загрузки, вычислителя знака определителя матрицы потокораспределения, вычислителя приращений и коррекции и вычислителя проверки сходимости, первый выход которого является первым выходом блока оценки предельных режимов, а второй выход соединен с дополнительным входом вычислителя предельного приращения коэффициента загрузки, а также вычислителя бифуркации, вход которого соединен с дополнительным выходом вычислителя знака определителя матрицы потокораспределения, а выход является вторым выходом блока оценки предельных режимов, при этом первый и второй выходы блока оценки предельных режимов соединены соответственно с первым и вторым входами блока памяти.

На чертеже представлены:

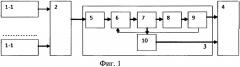
на фиг. 1 - функциональная схема автоматизированного устройства определения предельных режимов электрических систем;

на фиг. 2 - таблица результатов примера расчета предельных режимов для двухузловой системы.

Автоматизированное устройство определения предельных режимов электрических систем (фиг. 1) содержит группу блоков 1-1…1-n оперативной памяти, блок 2 сбора данных, блок 3 оценки предельных режимов и блок 4 памяти, при этом, выходы блоков 1-1…1-n оперативной памяти группы соединены с входом блока 2 сбора данных, выход которого соединен с входом блока 3 определения предельных режимов, первый и второй выходы которого соединены соответственно с первым и вторым входами блока 4 памяти.

В автоматизированном устройстве определения предельных режимов электрических систем блок оценки предельных режимов выполнен в виде последовательно соединенных вычислителя 5 вектора множителей Лагранжа, вход которого является входом блока 3 оценки предельных режимов, вычислителя 6 предельного приращения коэффициента загрузки, вычислителя 7 знака определителя матрицы потокораспределения, вычислителя 8 приращений и коррекции и вычислителя 9 проверки сходимости, первый выход которого является первым выходом блока 3 оценки предельных режимов, а второй выход соединен с дополнительным входом вычислителя 6 предельного приращения коэффициента загрузки, а также вычислителя 10 бифуркации, вход которого соединен с дополнительным выходом вычислителя 7 знака определителя матрицы потокораспределения, а выход является вторым выходом блока 3 оценки предельных режимов, при этом первый и второй выходы блока 3 оценки предельных режимов соединены, соответственно, с первым и вторым входами блока 4 памяти.

Предложенное техническое решение содержит в себе элементы, охарактеризованные на функциональном уровне, и описываемая форма реализации предполагает использование программируемого (настраиваемого) многофункционального средства, поэтому ниже при описании его работы представляются сведения, подтверждающие возможность выполнения таким средством конкретной предписываемой ему в составе данного технического решения функции, в частности алгоритмы и соответствующие математические выражения.

Автоматизированное устройство определения предельных режимов электрических систем работает следующим образом.

Предварительно проведем теоретическое обоснование алгоритма работы устройства.

Определение предельных режимов (ПР) играет ключевую роль в анализе, планировании и управлении электрическими системами. Предельный режим - есть такой статически устойчивый установившийся режим, в котором произвольное малое изменение любого текущего параметра в неблагоприятном направлении вызывает коллапс напряжений или потерю синхронизма блоками.

Один из наиболее обычно используемых подходов поиска ПР состоит в последовательном расчете установившихся режимов с заданным шагом вдоль заданной траектории, пока не разойдется расчет режима, который, в свою очередь, уточняется двоичным поиском или методом Ньютона по параметру. Однако, как только электрическая система подходит близко к условиям неустойчивости, расходимость расчета режима может быть вызвана плохой обусловленностью матрицы Якоби. Вот почему в методах последовательного утяжеления широко используется параметризация потокораспределения или нормализация изменения итерационного шага. В этом случае матрица Якоби в промежуточных и ПР является не вырожденной.

Модель электрической системы для определения предельных режимов может быть представлена следующим образом:

при условии

Здесь t - скаляр, обычно называемый коэффициентом загрузки.

Система (1, а) представляет уравнения баланса активных мощностей в PV и PQ узлах и уравнения баланса реактивных мощностей в PQ узлах; вектор X представляет углы напряжений узлов (кроме угла балансирующего узла) и модули напряжений PQ узлов; вектор Y представляет активную и реактивную мощность в каждом узле нагрузки и активную мощность, генерируемую в каждом генераторном узле; вектор направления dY представляет определенные пользователем изменения в электропотреблении активной и реактивной мощности и изменения в выработке активной мощности.

Функция Лагранжа задачи (1)-(1а) может быть представлена как

где λ - вектор вспомогательных переменных решений, называемых множителями Лагранжа.

Дифференцирование этой функции относительно всех переменных дает

Здесь - градиент функции Лагранжа относительно вектора X, - матрица Якоби потокораспределения.

Условие (3, б) гарантирует, что в точке решения задачи (1)-(1, а) вектор λ не будет равен нулю. Поэтому условие (3) определяет вырожденность матрицы Якоби потокораспределения, т.е. ПР.

В ПР матрица Якоби потокораспределения вырождена. В противоположность этому матрица системы линеаризованных уравнений (3)-(3, б)

не является вырожденной в точке решения задачи (1-1, а). Здесь есть матрица вторых частных производных (Гессе).

Уравнения (3)-(3, а) могут быть получены прямо из теоремы о неявной функции. При таком подходе они получили название уравнения ПР. В существующих модификациях условие (3) в некоторых случаях записывается для правого собственного вектора, отвечающего нулевому собственному значению, в то время как евклидова или бесконечность норма вектора λ используется как второе слагаемое в (3, б).

Исследования показали, что хорошие начальные предположения для переменных системы, особенно собственного вектора, являются существенными для получения решения системы нелинейных уравнений (3)-(3, б). Иначе итерационный процесс при использовании метода Ньютона для получения решения (3)-(3, б) или не даст искомого решения, или не сойдется. Поэтому до настоящего времени предпочтительным являлось использование методов последовательного утяжеления, по крайней мере, для нахождения первоначального ПР.

Рассмотрим 2-узловую систему с PV узлом k и балансирующим узлом m. В этом случае задача (1)-(1, а) будет иметь следующий вид:

при условии

,

где t - коэффициент загрузки; δ_k, V_k - угол напряжения и величина напряжения в узле k; Р_к есть активная мощность в узле k; dP_k есть данное «направление» изменения активной мощности для узла k; Y_km есть проводимость между узлами k и m; есть угол потерь; .

Функция Лагранжа для этой задачи может быть представлена как

,

Условия оптимальности первого порядка есть

Уравнение (5, б) немедленно определяет множитель Лагранжа . Поэтому, если использовать это значение как начальное приближение λ, тогда только два линеаризованных уравнения будут действительно использоваться во время итерационного процесса.

Согласно (6)

Подстановка (7) в (6, а) дает

В зависимости от исходного установившегося режима и данного направления dP_k множитель при Δδ_k в (6), который соответствует матрице Гессе [H] в (4), может быть положительной величиной или отрицательной величиной. Изменение режима (7) пойдет только в одном направлении независимо от заданного направления dP_k. В случае δ_km>α_km угол δ_km будет возрастать, следовательно, ПР будет соответствовать максимальной выработке активной мощности в узле k. В случае δ_km<α_km угол δ_km будет уменьшаться и ПР будет соответствовать максимальному потреблению в узле k. Установившийся режим с δ_km=α_km есть «пограничный режим» (BS) между областями притяжения к этим двум ПР. Якобиан (детерминант) линеаризованных уравнений (6) и (6, а) с учетом (5, б) равен . Поэтому в BS, т.е. когда δ_km=α_km, матрица линеаризованных уравнений (6)-(6, а) является вырожденной. В окрестности BS эта матрица плохо обусловлена. Поэтому в случае «легкого» исходного режима, когда δ_km≈α_km, приращения Δδ_k (7) и Δt (8) могут быть очень большими. В противоположность этому в ПР якобиан имеет самое высокое абсолютное значение. В близости ПР матрица системы (6)-(6, а) хорошо обусловлена и метод Ньютона имеет квадратичную скорость сходимости.

В прямоугольных координатах ПР будет также зависеть от начального установившегося режима. Угловое изменение больше одного периода невозможно, но коэффициент загрузки t и узловые напряжения могут существенно превысить расчетные значения. В близости ПР скорость сходимости оказалась ниже, чем в полярных координатах. Можно предположить, что использование t²dP является более успешным вариантом, чем tdP Однако это не дает желательного результата. Если начальная матрица Гессе [H] не является положительно определенной, колебательный итеративный процесс возникает вокруг BS δ_km=α_km, в случае положительно определенной матрицы [H] скорость сходимости оказалась заметно хуже, чем с tdP.

Таким образом, представленный анализ показывает, что для реализации задачи (1)-(1, а) необходимо решить две проблемы. Во-первых, итерационный процесс должен генерировать изменение переменных в "правильном" направлении. Во-вторых, при использовании системы линейных уравнений (4) необходимо использовать механизмы, учитывающие плохую обусловленность матрицы этой системы. В теории нелинейного программирования существует много реализующих это процедур. Однако обычная реализация этих процедур пока не позволила разработать вычислительно эффективный алгоритм решения задачи (1)-(1, а).

Существует два классических подхода для глобализации локально сходящего алгоритма: процедуры линейного поиска или использование доверительных областей. Первых подход требует использование merit-функции (выгодности). Выбор merit-функции неоднозначен и сильно влияет на скорость сходимости алгоритма. Второй подход связан с большим дополнительным объемом вычислений на каждой итерации, например, для обеспечения положительной определенности матрицы Гессе или требуемой инерции матрицы (4).

Вместе с тем, использование особенностей структуры системы линейных уравнений (4) и критерия оптимальности второго порядка задачи (1)-(1, а) позволяет получить простой, быстрый и надежный метод расчета ПР в заданном направлении изменения мощностей.

Рассмотрим метод определения ПР для случая одиночного балансирующего узла.

Представим систему линеаризованных уравнений (4) в следующем виде

Система нелинейных уравнений (3)-(3, б) есть условия оптимальности первого порядка для задачи (1)-(1, а). Согласно теории нелинейного программирования решение задачи (1-1, а) будет точкой строгого локального минимума, если

для любого вектора Z, который удовлетворяет следующее ограничение в виде равенства

где z_t есть любой скаляр. Требования (3)-(3, б) и (10)-(10, а) известны как достаточные условия оптимальности второго порядка.

В отличие от задачи безусловной оптимизации условия (10)-(10, а) не требуют положительно определенной матрицы Гессе [H] в точке решения. Достаточно иметь положительно определенную матрицу Гессе [H] вдоль направления Z.

Сравнение системы уравнения (10, а) с (9, а) показывает, что система (10, а) есть система (9, а) при ΔF=0, т.е. когда (9, а) является однородной. Поэтому, чтобы учесть условие (10) при решении задачи (1)-(1, а), можно представить вектор ΔХ в виде суммы двух векторов

где ΔX_dY и ΔХ_ΔF есть векторы решения следующих систем линейных уравнений:

Подстановка (11) в (9) дает

В свою очередь, подстановка (13) в (9, б) дает

где .

Сравнение (10, а) с (12) показывает, что ΔX_dY=Z/Z_t. Следовательно, . Поэтому, чтобы обеспечить изменение переменных в «правильном» направлении, необходимо, согласно требованию (10), чтобы знаменатель в (14) был положительным. Если это не так, необходимо его «подкорректировать». Наиболее простой подход, который в тоже самое время имеет теоретическое обоснование, есть увеличение каждого диагонального элемента матрицы Гессе [H] на положительную β>0 в (9). В этом случае изменится выражение (13) и уравнение (14) примет вид

где - Евклидова норма.

Значение β может быть выбрано различными способами, основное требование есть

Но это требование является недостаточным для надежной сходимости метода.

Анализ 2-узловой системы показал, что матрица линейных уравнений (4), а значит (9)-(9, б), вырождена в BS. Для (14) это означает, что знаменатель будет равен нулю. В окрестности BS эта матрица плохо обусловлена и значение знаменателя (14) будет значительно меньше 1. Как следствие, изменение переменной Δt, а значит ΔХ и Δλ в соответствии с (11) и (13) будут очень большими. Согласно (14, а) величина β позволяет уменьшить величину Δt, т.е. улучшить число обусловленности системы (9)-(9, б). Для этого можно воспользоваться идеологией доверительных областей. Если тем или иным способом допустимое значение Δt_max определено, значение β может быть получено непосредственно из (14, а).

Так как расстояние к ПР не известно заранее и значение dY может быть выбрано произвольное, лучшим решением будет адаптивное переназначение величины Δt_max после определения ΔX_dY из (12) с тем, чтобы ограничить максимальное изменение углов напряжения или других параметров режима на итерации.

После определения Δt (14а), вектор ΔХ находится из (11), а вектор λ - из решения системы линейных уравнений

Коэффициент загрузки t линейно включен в уравнение (3, а). После итерации он изменится в соответствии с линеаризованными выражениями (9, а), где нелинейные изменения не учтены. Поэтому после итерации значение t может быть скорректировано на величину

Это уменьшает Евклидову норму вектора небаланса мощностей на итерации и вектор небалансов мощностей становится ортогональным вектору dY, что также улучшает число обусловленности.

Рассмотрим метод определения ПР для случая распределенного балансирующего узла. В случае распределенного балансирующего узла узловые уравнения потокораспределения (1, а) принимают следующую форму:

где P^S - мощность балансирующего узла; α^S - коэффициенты участия узлов в распределенном балансирующем узле с и

Когда (19) будет использован для задачи (1-1, а), условие (3, б) останется неизменным, (3, а) будет заменен (19), и (3) будет дополнен следующим уравнением:

Векторы ΔX_dY и ΔX_ΔF в уравнениях (11), (14,а), и (16) могут быть получены из решения следующих систем линейных уравнений:

; ,

где - матрица Якоби потокораспределения с распределенным балансирующим узлом.

Вектор множителей Лагранжа получается путем решения следующей системы линейных уравнений:

.

Изменение мощности распределенного балансирующего узла на итерации определяется следующим выражением:

.

Подобно коэффициенту загрузки мощность распределенного балансирующего узла линейно включена в уравнение (19). Именно поэтому после итерации ее значение может быть скорректировано на величину , тем самым компенсируя проекцию вектора невязок мощностей на вектор α^S.

Проведем учет индуцированной пределом бифуркации.

Учет ограничений реактивной мощности генераторов выполняется так же, как при обычном расчете потокораспределения. Однако если ПР соответствует индуцированной пределом бифуркации (LIB), то может возникнуть ситуация, когда не будет наблюдаться сходимость из-за особенностей LIB: по крайней мере один из генераторных узлов будет переключать свой тип из PV в PQ и обратно, причем неоднократно. Такая ситуация возникает, когда отдельный генератор m достигает своего предела максимальной реактивной мощности ; dQ_m/dt>0, где Q_m есть реактивная мощность, вырабатываемая этим генератором, матрица Якоби не вырождена и, если генератор m переключится с PV типа в PQ⁺ тип, определитель матрицы Якоби изменит знак (когда мощности нагрузки имеют положительный знак в уравнениях потокораспределения), dV_m/df>0. Учет этих особенностей позволил разработать следующую процедуру выявления и определения LIB.

Проверка LIB начинает выполняться, если определитель матрицы Якоби изменил знак. Используя ΔХ из (11), выявляются генераторы PQ⁺-типа, напряжение которых превысит установленные заданные значения на итерации. Если такие генераторы не обнаружены, это не LIB и итерация процедуры определения ПР продолжается. С другой стороны, эти генераторы переключаются с PQ⁺ типа в PV тип, и выполняется следующая процедура определения LIB.

Шаг 1. Решается (12)-(12а) и вычисляется

,

где ∇_XQ_k есть градиент уравнения баланса реактивной мощности узла k относительно X, .

Определяется ΔХ=ΔX_ΔF+tΔX_dY и модифицируется X.

Шаг 2. Проверяются ограничения по реактивной мощности генераторов PQ-типа. Если какие-то ограничения нарушены, тип соответствующих генераторов переключается и следует возвратиться к шагу 1, иначе процедура продолжается.

Шаг 3. Вычисляется , k⊂PV. Если , то следует вернуться шагу 1, иначе процедура продолжается.

Шаг 4. Переключается тип генератора m с PV в PQ⁺ и решается (12). Если ΔV_m<0, тогда следует возвратиться к шагу 1; иначе остановка и LIB определена (предел реактивной мощности узла m индуцирует бифуркацию).

Таким образом, если принять во внимание процедуру выявления и определения LIB, алгоритм процедуры определения ПР может быть представлен следующим образом.

Шаг 0. Рассчитывается (задается) исходный установившийся режим и вычисляется начальное приближение λ обратным степенным методом.

Шаг 1. Решается (12)-(12а) и вычисляется Δt_max, используя ΔX_dY, а затем Δt и ΔХ, используя (16), (14, а), и (11).

Шаг 2. Если определитель матрицы Якоби изменил знак, тогда выполняется частная процедура выявления и определения LIB, что соответствует окончанию основной процедуры определения ПР, иначе процедура продолжается.

Шаг 3. Решается (17) для получения Δλ, модифицируются t, X и λ, затем корректируется t по соотношению (18). Проверяются ограничения реактивной мощности генераторов и, в случае необходимости, изменяют их тип

Шаг 4. Проверяется сходимость: если , то основная процедура заканчивается, иначе необходимо возвратиться к шагу 1.

Указанный алгоритм реализуется в предложенном устройстве следующим образом.

В автоматизированном устройстве определения предельных режимов электрических систем в блоки 1-1…1-n оперативной памяти группы (фиг. 1) заносятся текущие параметры сети, которые собираются в блоке 2 сбора данных в виде исходных данных для проведения расчетов в блоке 3 оценки предельных режимов. Полученные оценки предельных режимов заносятся в блок 4 памяти.

В вычислителе 5, вход которого является входом блока 3 оценки предельных режимов, определяется начальное приближение вектора множителей Лагранжа λ, например, обратным степенным методом. Это позволяет в вычислителе 6 предельного приращения коэффициента загрузки путем решения системы (12)-(12а) вычислить Δt_max, используя ΔX_dY, а затем Δt и ΔХ, используя (16), (14, а) и (11). В вычислителе 7 знака определителя матрицы потокораспределения устанавливается, изменился ли знак определителя матрицы Якоби. При условии, что определитель матрицы Якоби изменил знак, в вычислителе 10 бифуркации выполняется частная процедура выявления и определения LIB, что соответствует окончанию основной процедуры определения ПР и занесению сигнала с выхода вычислителя 10 в блок 4 памяти. В противном случае процедура определения ПР продолжается в вычислителе 8 приращений и коррекции, в котором решается (17) для получения Δλ, модифицируются t, Х и λ, а затем корректируется t по соотношению (18). Здесь же проверяются ограничения реактивной мощности генераторов и, в случае необходимости, изменяется их тип. После этого сигнал с выхода вычислителя 8 поступает на вход вычислителя 9 для проверки сходимости: если и , то скорректированное значение t заносится в блок 4 памяти, что означает окончание основной процедуры определения ПР, иначе производится передача сигнала в вычислитель для продолжения вычислений с учетом модификации и корректировки t, X и λ.

Рассмотрим пример использования предложенного устройства для двухузловой электрической системы. В таблице (фиг. 2) показан результат его использования при нахождении ПР в заданном направлении изменения (увеличение генерации) мощности в узле k. Узловые данные и результаты представлены для следующих параметров системы: , V_k=V_m=110 kV, P_k=100 MW, dP_k=10 MW, α_km=26.565°, , .

Система имеет два ПР. Один соответствует максимальной генерации в узле k, другой - максимальной нагрузке в этом узле. Режим максимальной генерации получается, когда , при этом генерируемая мощность будет равна . Режим максимальной нагрузки получается, когда δ_km-α_km=-π/2, при этом максимальная нагрузка в узле k будет равна . В «пограничном» режиме (BS), т.е. когда , узел k генерирует мощность . Таким образом, BS оказывается равноудаленным от этих двух ПР.

В базисном режиме узел k генерирует 100 MW. Поскольку , этот режим оказывается ближе ко второму ПР. В исходном режиме . Угол потерь линии α_km=26.565°. Поскольку δ_km<α_km, то решением системы (3) должен быть ПР в противоположном заданному направлению изменения мощностей. Т.е. модель (1)-(1, а) движет режим электрической системы к ближайшему ПР в пространстве мощностей. Более того, матрица системы (4) плохо обусловлена в исходном режиме. Величина знаменателя (14) равна . Если не использовать величину β, решение системы (4) будет Δt¹,=-346.595 и на первой итерации. Т.е. угол δ_km провернется в «неправильном» направлении больше чем два раза. Предложенное устройство легко преодолевает эти трудности. Из таблицы (фиг. 2) видно, что на первой итерации имеет отрицательное значение. Поэтому, согласно (16), матрица [H] «подправляется» с помощью β. Для того чтобы улучшить число обусловленности, на каждой итерации значение Δt_max находилось из условия, чтобы изменение углов (ΔX_dYΔt) по линии не превышало 45°. На второй итерации значение стало положительным, и β использовалась для улучшения числа обусловленности. Всего потребовалось 3 итерации для расчета ПР. После третьей итерации величина небаланса мощности равна 3.189*10^-3 MW, а собственное значение матрицы Якоби потокораспределения достигло практически нулевого значения, а именно - 1.032*10^-5. Таким образом, предложенное устройство обеспечивает быстрый, надежный и точный расчет ПР. Точность легко подтверждается выражением , которое должно выполняться в этом ПР. После третьей итерации угол δ_km в точности равен этой величине.

Таким образом, благодаря введению дополнительного арсенала технических средств (в частности, тем, что выходы блоков оперативной памяти группы соединены с входом блока сбора данных, выход которого соединен с входом блока оценки предельных режимов, выход которого соединен с входом блока памяти, а блок оценки предельных режимов выполнен в виде последовательно соединенных вычислителя вектора множителей Лагранжа, вход которого является входом блока оценки предельных режимов, вычислителя предельного приращения коэффициента загрузки, вычислителя знака определителя матрицы потокораспределения, вычислителя приращений и коррекции и вычислителя проверки сходимости, первый выход которого является первым выходом блока оценки предельных режимов, а второй выход соединен с дополнительным входом вычислителя предельного приращения коэффициента загрузки, а также вычислителя бифуркации, вход которого соединен с дополнительным выходом вычислителя знака определителя матрицы потокораспределения, а выход является вторым выходом блока оценки предельных режимов, при этом первый и второй выходы блока оценки предельных режимов соединены, соответственно, с первым и вторым входами блока памяти), достигается требуемый технический результат, связанный с повышением быстродействия устройства при определении предельных режимов (ПР) электрических систем, что подтверждено экспериментально.

Автоматизированное устройство определения предельных режимов электрических систем, содержащее группу блоков оперативной памяти, блок сбора данных и блок памяти, а также блок оценки предельных режимов, отличающееся тем, что выходы группы блоков оперативной памяти соединены с входом блока сбора данных, выход которого соединен с входом блока оценки преде