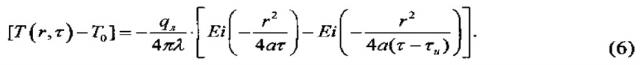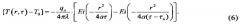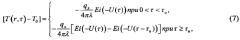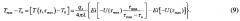Способ измерения теплофизических свойств анизотропных материалов методом линейного импульсного источника теплоты

Способ измерения теплофизических свойств анизотропных материалов методом линейного импульсного источника теплоты

Иллюстрации

Показать все

Реферат

Изобретение относится к области исследования теплофизических характеристик анизотропных материалов.

Известен способ определения комплекса теплофизических свойств твердых материалов [Патент РФ №2125258, кл. G01N 25/18, 1999], включающий воздействие тепловыми импульсами от линейного источника на плоскую поверхность исследуемого и эталонного образцов, измерение избыточных температур в моменты подачи тепловых импульсов в точках, расположенных на фиксированных расстояниях от линии нагрева на поверхности образцов. Измеренные температуры приближают с минимальной погрешностью к рассчитанным температурам, формируемых посредством программного управления параметрами теплофизических характеристик. По идентифицированным параметрам образцов и действительным значениям характеристик эталона определяют искомые характеристики.

Недостатками этого способа являются большая длительность и трудоемкость эксперимента, а также необходимость использования эталонного образца.

Известен способ измерения теплофизических свойств твердых материалов, методом линейного мгновенного источника тепла [Пономарев, С.В. Теоретические и практические основы теплофизических измерений: монография / под ред. С.В. Пономарева. - М.: ФИЗМАТЛИТ, 2008. - 408 с.], заключающийся в том, что из исследуемого материала изготавливают две массивные пластины (их толщина должна на менее чем в десять-двадцать раз превышать расстояние r между электронагревателем и измерителем температуры). Нагреватель и измеритель температуры размещают на расстоянии r друг от друга между этими двумя пластинами. Получившуюся систему в течение достаточно длинного промежутка времени выдерживают при необходимой постоянной температуре T₀. Затем на линейный электронагреватель длиной L подают постоянную мощность P в течение заданного малого промежутка времени 0<τ≤τ_u и регистрируют изменение во времени разности температур [T(r,τ)-T₀] по сигналу измерителя температуры. По полученным экспериментальным данным определяют максимальное значение разности температур [T_max-T₀]=[T(r,τ_max]-T₀] и значение момента времени τ=τ_max, соответствующее этому максимальному значению [T_max-T₀], а также количество теплоты Q_л=q_л⋅τ_u, выделившейся в единице длины электронагревателя. По полученным значениям τ_max, [T_max-T₀], с учетом известных r, Q_л, вычисляют искомые значения коэффициентов температуропроводности a и теплопроводности λ исследуемого материала.

Недостатками данного способа является то, что значение момента времени τ=τ_max по экспериментальным данным определяется с высокой относительной погрешностью, зачастую достигающей величины (15…20)%, а также то, что отсутствуют рекомендации по выбору рационального конструкционного размера r.

Наиболее близким техническим решением является способ измерения теплофизических свойств твердых материалов методом линейного мгновенного источника тепла [Пономарев С.В., Исаева И.Н., Мочалин С.Н. О выборе оптимальных условий измерения теплофизических свойств веществ методом линейного «мгновенного» источника тепла // Заводская лаборатория. Диагностика материалов.- 2010. - Т. 76, №5, С. 32-36], заключающийся в том, что из исследуемого материала изготавливают две массивные пластины, между которыми размещают линейный электронагреватель и измеритель температуры на расстоянии r друг от друга. Получившуюся систему на подготовительной стадии эксперимента в течение достаточно длинного промежутка времени выдерживают при необходимой постоянной температуре T₀. Затем на линейный электронагреватель подают постоянную мощность в течение заданного малого промежутка времени 0<τ≤τ_u и регистрируют изменение во времени разности температур [T(r,τ)-Т₀] по сигналу измерителя температуры. Так как определение значения τ_max приводит к большим погрешностям, находят два момента времени τ' и τ'', для чего вводят параметр , где T_max - максимальное значение температуры, достигаемое в ходе эксперимента в момент времени τ_max. Были выведены математические модели, связывающие погрешности измерения температуропроводности и объемной теплоемкости с погрешностями измерения температуры, плотности источника тепла, геометрического размера r, а также сформулированы рекомендации по выбору оптимальных режимных и конструкционных параметров α_опт и r_опт.

Основным недостатком данного способа является то, что в математической модели температурного поля внутренний источник теплоты задается в виде линейного мгновенного импульса, хотя в действительности теплота подводится к нагревателю в течение промежутка времени 0<τ<τ_u, где τ_u - длительность реального (не мгновенного) теплового импульса, подводимого к нагревателю. До настоящего времени не рассматривались вопросы о выборе оптимального значения длительности τ_u теплового импульса.

Другим недостатком этого способа является то, что нет рекомендаций о том, как долго исследуемый образец на подготовительной стадии эксперимента надо выдерживать при постоянной температуре T₀.

Техническая задача изобретения - повышение точности измерения теплофизических свойств анизотропных материалов за счет выбора оптимальных режимных параметров теплофизического эксперимента и рационального конструкционного размера, измерительного устройства, а также сокращение продолжительности подготовительной стадии эксперимента за счет использования критерия E_i.

Физическая модель измерительного устройства представляет собой ячейку, в которую помещают образец, состоящий из двух пластин: нижней и верхней. Между верхней гранью нижней пластины и нижней гранью верхней пластины помещают линейный электронагреватель (выполненный, например, в виде тонкой металлической проволоки из нихрома, манганина или константана), а на расстоянии r от нагревателя в этой же плоскости размещают измеритель температуры (в виде термометра сопротивления из медной проволоки).

Математическая модель температурного поля T(r,τ) в исследуемом материале (в случае использования импульсного линейного источника теплоты) может быть записана в виде:

где r, τ - пространственная координата образца и время; cρ, λ - объемная теплоемкость и теплопроводность исследуемого материала; T₀ - первоначальная температура материала (в момент времени τ=0), принимаемая за начало температурной шкалы в каждом эксперименте, то есть T₀=0; Q_л - суммарное количество теплоты, выделившееся в единице длины линейного нагревателя при r=0 в момент времени τ=0; δ(r), δ(τ) - символические дельта-функции Дирака, τ_u - длительность реального (не мгновенного) теплового импульса, подводимого к нагревателю.

Решение краевой задачи (1)-(4) при непрерывно действующем постоянном источнике теплоты W(r,τ)=q_лδ(r-0)⋅h(τ-0), имеет вид

где - количество теплоты, выделяемое единицей длины L линейного источника теплоты в единицу времени; - коэффициент температуропроводности; h(τ-0) - единичная ступенчатая функция, имеющая вид:

Если (в случае рассматриваемого в статье импульсного источника теплоты длительность 0<τ≤τ_u) задать W(r,τ)=q_лδ(r-0)[h(t)-h(t-τ_u)], то на основании принципа суперпозиции и известного решения (5), получаем:

Таким образом, общее решение задачи (1)-(4) с учетом (5) и (6) принимает вид:

где - интегральная показательная функция, , - безразмерные функции, зависящие от r, τ, τ_u, a, причем, .

Разработанная методика обработки экспериментальных данных базируется на использовании безразмерного параметра

который представляет собой отношение разности температур [T(r,τ')-Т₀] (в момент времени τ') к максимальному значению разности температур [Т(r,τ_max)-Т₀]=[T_max-T₀], имеющему место в момент времени τ=τ_max.

Причем каждой величине разности температур γ⋅[T_max-T₀]=[T(r,τ')-T₀], то есть каждому значению безразмерного параметра γ, соответствует конкретное значение момента времени τ'.

При математическом моделировании процесса измерения ТФС сначала с постоянным шагом Δτ во времени τ по формуле (7) вычисляли и регистрировали (в виде массивов) значения разностей температур [T(r,τ_i)-Т₀] и моментов времени τ_i, i=1, 2, …, n, а затем, по массиву полученных данных [T(r,τ_i)-Т₀], i=1, 2, …, n, находили максимальное значение [T_max-Т₀] этой разности. После этого методом интерполяции находили значение момента временит τ', соответствующее величине разностей температур [T(r,τ')-Т₀]=γ⋅[T_max-T₀], которое аналитически можно записать в виде

Поделив зависимость (7) при τ>τ_u на (9) получаем, что

Если известны из эксперимента длительность τ_u теплового импульса, значения разности температур T(r,τ_i)-T₀], и соответствующие им значения моментов времени τ_i, i=1, 2, …, n, то путем решения уравнения (10) находим значение безразмерной величины

соответствующее заданной величине параметра γ, причем значение τ'=τ'(γ) является функцией величины параметра γ.

Из (11) следует расчетное соотношение для вычисления коэффициента температуропроводности

После преобразования соотношения (6), была получена формула для вычисления объемной теплоемкости

После получения формул (12) и (13) определим, при каком значении безразмерного параметра γ будут иметь место минимальные погрешности измерения искомых значений a и cρ коэффициента температуропроводности и объемной теплоемкости.

В соответствии с рекомендациями методик вывода формул для вычисления относительных погрешностей измерения ТФС были получены соотношения для вычисления среднеквадратичных оценок относительных погрешностей (δa)_ск и (δcρ)_ск измерения температуропроводности a и объемной теплоемкости cρ, имеющие вид:

В процессе работы стало очевидно, что относительные среднеквадратичные погрешности (δсρ)_ск измерения объемной теплоемкости сρ существенно зависят от длительности τ_u теплового импульса.

При осуществлении измерений желательно обеспечить выполнение требования о подведении к линейному нагревателю такой величины мощности P, при которой достигаемая в момент времени τ=τ_max в ходе каждого эксперимента максимальная разность температур [T(r,τ_max)-T₀]=[T_max-T₀] на расстоянии r от нагревателя остается примерно одинаковой и находится в определенных пределах, что необходимо по следующим причинам:

- если эта максимальная разность [T_max-T₀] мала, то относительные погрешности измерения значений разностей температур [T(r,τ)-T₀] будут слишком большими, что может привести к росту относительных погрешностей (δa)_ск, (δcρ)_ск измерения искомых теплофизических свойств (ТФС);

- если же эта максимальная разность [T_max-T₀] окажется слишком большой, то не будет выполнено предположение о том, что процессы переноса теплоты в образце описываются линейной математической моделью (1)-(4), что опять же приведет к возрастанию результирующих погрешностей (δa)_ск, (δcρ)_ск измерения искомых ТФС из-за нелинейностей, не учитываемых линейной краевой задачей (1)-(4).

Для выполнения этого требования (что [T_max-T₀]≈const) при каждом значении длительности τ_u теплового импульса линейный нагреватель должен обеспечивать создание удельной мощности при которой внутри образца в единице длины нагревателя в каждом эксперименте выделяется постоянное суммарное количество теплоты

где q_л - удельная мощность, подводимая нагревателем мощностью P и длиной L к образцу в течение промежутка времени 0≤τ≤τ_u.

Проведенные численные расчеты показали, что при исследовании образцов теплоизоляционных материалов с расстоянием от нагревателя до измерителя температуры 3≤r≤6 мм для получения разности температур [T_max-T₀]=3…7°C, суммарное количество теплоты Q_л, выделяющееся в единице длины L электронагревателя, следует поддерживать в пределах . Поэтому приведенные на фиг. 1 и фиг. 2 данные и результаты определения оптимального значения , обеспечивающего получение минимальных погрешностей (δa)_ск и (δcρ)_ск измерения a и cρ, были получены при .

Рассмотрим подробнее вычисление составляющей погрешности δq_л, входящей в формулу (15). Из изложенного выше следует

т.е. . При этом электрическую мощность P, подведенную к плоскому нагревателю, следует выбирать из соотношения , причем при , L=0.06 м получается, что

После логарифмирования (17), определения дифференциалов от левой и правой частей получившегося соотношения и выполнения других рекомендаций теории погрешностей получаем формулу

в которой величину P(τ_u) вычисляли по формуле (18). После подстановки (19) в (16), получаем

С использованием полученных формул (14) и (20) были рассчитаны зависимости от безразмерного параметра γ среднеквадратичных относительных погрешностей (δa)_ск, (δcρ)_ск, при длительности теплового импульса τ_u=21 c. Результаты расчетов представлены на фиг. 1. При этом в расчетах были использованы следующие исходные данные: , , ΔP=0,1 Вт; r=(2…8) мм, Δr=0,1 мм; ΔT=0,05 K, δL=0,5%.

Из фиг. 1 видно, что минимальные значения относительных погрешностей (δa)_ск, (δcρ)_ск зависят не только от параметра γ, но и от величины расстояния r между линейным импульсным нагревателем и измерителем температуры. В связи с этим было принято решение построить линии равных уровней погрешностей на плоскости с координатами (γ, r) для длительности теплового импульса τ_u=21 с. Результаты этой работы представлены на фиг. 2.

Представленные на фиг. 2 результаты вычислений показывают, что (при использованных в расчетах исходных данных) минимальные значения среднеквадратичных относительных погрешностей (δa)_ск измерения коэффициента температуропроводности a достигаются при значениях безразмерного параметра γ^a в диапазоне 5.4 мм<r<6.0 мм, и при значениях основного конструкционного размера измерительного устройства в пределах 5.4 мм<r<6.0 мм, причем , .

В то же время минимальные значения среднеквадратичных относительных погрешностей (δcρ)_ск измерения объемной теплоемкости cρ имеют место при 0,72<γ^cρ≤0,80 и 5,0≤r≤5,6, причем , .

Таким образом, для достижения минимальных значений погрешности (δa)_ск и (δсρ)_ск при измерении коэффициента температуропроводности a и объемной теплоемкости cρ исследуемого материала следует использовать измерительный преобразователь с расстоянием между измерителем температуры и нагревателем в диапазоне 5,4 мм≤r≤5,6 мм, причем можно принять .

Для определения оптимального значения длительности τ_u теплового импульса, обеспечивающего достижение минимальных значений относительных погрешностей (δa)_ск, (δсρ)_ск и среднеарифметических значений погрешностей измерения теплофизических свойств a и cρ, были выполнены расчеты по формулам (14) и (20), результаты которых представлены на фиг. 3.

Из фиг. 3 видно, что при изменении длительности τ_u теплового импульса среднеарифметическое значение погрешностей принимает минимальные значения при τ_u^опт≈21 с, находящемся в диапазоне 18 с<τ_u<24 с.

Таким образом, при измерении теплофизических свойств исследуемого анизотропного материала следует поступать следующим образом:

- на подготовительной стадии эксперимента измеряют значения разностей температур с постоянным шагом во времени Δτ и, начиная с n-го шага, контролируют величину показателя , n = const выбирают из диапазона 2≤n≤10 и, при выполнении критерия E_i≤0,01, переходят к активной части эксперимента, для чего на линейный электронагреватель подают электрический импульс, длительность которого находится в диапазоне 18≤τ_u≤24 с;

- на протяжении активной стадии эксперимента измеряют и регистрируют с постоянным шагом во времени разность температур [T(r,τ_i)-T₀] и по полученным данным находят максимальное значение этой разности [T_max-Т₀]=[T(r,τ_max)-Т₀];

- путем проведения предварительных измерений определяют ориентировочные значения коэффициента температуропроводности a_ор и объемной теплоемкости cρ_ор исследуемого материала по формулам:

,

,

где , , U(τ'), U(τ'') - безразмерные функции, определяемые при заданных ориентировочных значениях параметров и из (10);

- находят величину и расстояние между линейным электронагревателем и измерителем температуры из зависимости

- определяют величину и значение расстояния , а также оптимальную длительность теплового импульса из зависимости

;

- расстояние между измерителем температуры и линейным нагревателем рассчитывают как среднее значение ;

- изготавливают измерительный преобразователь с расстоянием между измерителем температуры и линейным нагревателем ;

- путем проведения серии экспериментов, при нескольких вариантах ориентации линейного электронагревателя и измерителя температуры относительно главных осей симметрии образца, осуществляют измерения и последующую обработку полученных данных при найденных значениях , , , и, в результате, получают таблицу значений искомых коэффициента температуропроводности a и объемной теплоемкости cρ исследуемого материала по формулам

,

,

характеризующую зависимость температуропроводности а анизотропного материала от ориентации линейного нагревателя и измерителя температуры относительно главных осей симметрии образца.

Отсутствие зависимости объемной теплоемкости ср исследуемого материала от ориентации линейного нагревателя и измерителя температуры относительно главных осей симметрии образца свидетельствует о том, что в процессе эксперимента были верно выдержаны условия его проведения.

Способ измерения теплофизических свойств анизотропных материалов методом линейного импульсного источника теплоты, заключающийся в том, что образец исследуемого материала изготавливают в виде двух массивных пластин, между этими пластинами размещают линейный электронагреватель длиной L и измеритель температуры на расстоянии r друг от друга, при этом толщина пластин должна не менее, чем в десять-двадцать раз превышать расстояние r, на подготовительной стадии эксперимента полученную систему помещают в воздушный термостат и выдерживают при заданной начальной температуре T₀, затем на электронагреватель подают электрический импульс, в течение активной стадии эксперимента с постоянным шагом во времени осуществляют измерение и регистрацию изменения во времени разности температур [T(r,τ_i)-T₀], по полученным данным находят максимальное значение этой разности [T_max-Т₀]=[T(r,τ_max)-T₀] и осуществляют обработку полученных данных, отличающийся тем, что на подготовительной стадии эксперимента с постоянным шагом во времени Δτ измеряют разности температур и, начиная с n-го шага, контролируют величину показателя , n=const выбирают из диапазона 2≤n≤10 и, при выполнении критерия E_i≤0,01, на линейный электронагреватель подают тепловой импульс мощностью , где Q_л=1000…2000 [Дж/м] - количество теплоты, выделяющееся в единице длины электронагревателя, длительность теплового импульса задают в диапазоне 18≤τ_u≤24 с, определяют ориентировочные значения коэффициента температуропроводности а_ор и объемной теплоемкости сρ_ор исследуемого материала по формулам:

;

,

где , , - удельная мощность, подводимая нагревателем мощностью Р и длиной L к образцу в течение промежутка времени 0≤τ≤τ_u, U(τ'), U(τ'') - безразмерные функции, определяемые при заданных ориентировочных значениях параметров и из уравнений

и , после чего из зависимости находят величину и расстояние между линейным электронагревателем и измерителем температуры , а из зависимости определяют величину и значение расстояния , а также оптимальную длительность теплового импульса , расстояние между измерителем температуры и линейным нагревателем рассчитывают как среднее значение , а затем, путем проведения серии экспериментов, при нескольких вариантах ориентации линейного электронагревателя и измерителя температуры относительно главных осей симметрии образца, осуществляют измерения и последующую обработку полученных данных при найденных значениях , , , и, в результате, получают таблицу значений искомых коэффициента температуропроводности а и объемной теплоемкости сρ исследуемого материала по формулам

,

,

характеризующую зависимость температуропроводности а анизотропного материала от ориентации линейного нагревателя и измерителя температуры относительно главных осей симметрии образца.