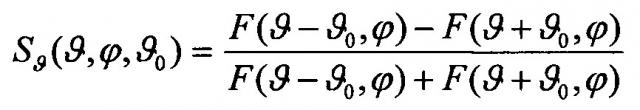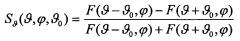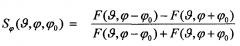Способ одновременного измерения двух угловых координат цели в обзорной амплитудной моноимпульсной радиолокационной системе с антенной решеткой и цифровой обработкой сигнала

Способ одновременного измерения двух угловых координат цели в обзорной амплитудной моноимпульсной радиолокационной системе с антенной решеткой и цифровой обработкой сигнала

Иллюстрации

Показать все

Реферат

Изобретение относится к области радиотехники и может быть применено при одновременном измерении двух угловых координат (УК) цели в системах моноимпульсной радиолокации и радиопеленгации, использующих цифровые антенные решетки (АР) или аналоговые АР с цифровой обработкой сигналов.

Определение направления на цель, как указывалось еще в работе [1 - Леонов А.И., Фомичев К.И. Моноимпульсная радиолокация. - М.: Радио и связь, 1984. 312 с, стр. 5], является одной из основных задач радиолокации. Радиолокационные системы (РЛС) должны определять УК целей с высокой точностью и за малое время, так как современные цели могут перемещаться с большими (в том числе гиперзвуковыми) скоростями и двигаться по сложным непредсказуемым траекториям, причем закон движения целей может содержать знакопеременные производные высоких порядков.

Лучшей основой для достижения высокой точности определения УК считается широко применяемый в радиолокации и радиопеленгации моноимпульсный метод, совершенствование которого продолжается в настоящее время. Этот метод применяется и в обзорных РЛС, которые определяют УК всех целей, находящихся в пределах диаграммы направленности (ДН) и разрешаемых по дальности [1, стр. 6]; в них используется прямоотсчетный подход, обеспечивающий существенно большую, чем компенсационный подход, скорость измерений.

В то же время отмечалось [1, стр. 127], что «моноимпульсные РЛС не используют своих потенциальных возможностей в быстродействии и извлекают угловую информацию о цели из серии последовательных импульсов». Проблема быстродействия существует и в настоящее время, ее решением была бы реализация потенциально возможного измерения двух УК цели по единственному импульсу.

Пути достижения высоких точностей и быстродействия обзорного амплитудного моноимпульсного пеленгатора для случая измерения одной УК показаны в работе [2 - Джиоев А.Л., Яковленко В.В. Улучшение характеристик обзорного суммарно-разностного пеленгатора с ФАР на основе оптимизации пеленгационной характеристики // Общие вопросы радиоэлектроники. Ростов-на-Дону: ФГУП «РНИИРС» ФНПЦ. 2014. Вып. 1. С. 105-117], где с помощью выбора вида весовой функции (ВФ) и оптимизации угла разноса ДН получена пеленгационная характеристика (ПХ), практически линейная на всей ширине моноимпульсной группы лучей (МГЛ). Это позволяет использовать прямоотсчетный подход и обеспечить быстрый прямой (без использования итераций и повторных импульсов) и легко реализуемый (решение линейного уравнения) расчет одной УК с ошибкой не более 1/100 ширины ДН по уровню половинной мощности при низком уровне боковых лепестков (ниже минус 40 дБ) и приемлемом использовании поверхности антенны.

Естественно предположить, что при обеспечении линейности ПХ одновременно по обеим угловым координатам в РЛС может быть реализован истинно моноимпульсный метод измерения, обладающий упомянутыми положительными свойствами. Однако, как показано ниже, в двухкоординатном случае только линейности ПХ недостаточно для реализации измерения по единственному импульсу - приходится жертвовать либо точностью, либо скоростью измерений, поскольку процесс измерений одной УК в общем случае зависит от значения другой УК относительно общего равносигнального направления (РСН).

Таким образом, вопросы обеспечения высокой точности и быстродействия обзорных амплитудных моноимпульсных РЛС при измерении одновременно двух УК цели являются актуальными.

В работе [1, стр. 76] указано, что моноимпульсные системы для пеленгации цели в двух плоскостях создаются простой комбинацией двух моноимпульсных систем, одна из которых работает в азимутальной плоскости, а вторая - в угломестной. Поэтому сначала рассмотрим аналоги предлагаемого изобретения, обеспечивающие определение УК цели в одной из координатных плоскостей.

Известен способ измерения угловой координаты объекта [3 - патент 2274874, РФ. Способ измерения угловой координаты объекта и РЛС для его реализации / Кисляков В.И., Лужных C.H., Прудников С.Я.], являющийся аналогом заявляемого способа. В способе [3] используется излучение зондирующих сигналов, поступающих от передатчика через антенный переключатель в фазированную АР, прием отраженных от цели сигналов не менее чем при двух последовательных угловых положениях луча и дополнительное определение величины отклонения луча от нормали антенны. Затем с учетом изменения ширины луча вычисляют УК объекта.

Заметим, что учет изменения ширины ДН, предлагаемый в аналоге [3], не является предметом заявляемого изобретения, хотя он может быть реализован в нем путем замены значения угловой координаты на ее синус.

Недостатками аналога [3] являются низкие (из-за чувствительности к флюктуациям сигнала, поскольку метод не является моноимпульсным) скорость и точность определения УК, что делает невозможным, при использовании его для определения УК в двух плоскостях, одновременное измерение обеих УК цели с ошибкой не более 1% ширины ДН (по уровню половинной мощности) за один импульс.

Известен также способ измерения угловых координат в обзорной моноимпульсной РЛС [4 - патент 2270458, РФ. Способ измерения угловых координат целей в моноимпульсной обзорной РЛС и моноимпульсная обзорная РЛС / Адодин В.М., Валов C.B., Нестеров Ю.Г., Пономарев Л.И., Юрк В.И.], в котором сформированный в передатчике СВЧ сигнал подается через антенный коммутатор к антенне, содержащей зеркало с 2-рупорным облучателем. Для определения УК целей используется компенсационный подход, при котором последовательно изменяют угловое положение РСН, осуществляют пороговое обнаружение сигнала и, используя пеленгационные отсчеты, селектируют положение цели на ПХ. Затем оцифровывают амплитуды сигналов, записывают их в память, после достижения РСН конца сектора обзора по результатам записи итерациями находят сигналы целей и их УК, а также, как указано в [4], находят уравнение прямой, аппроксимирующей поведение пеленга в зависимости от ориентации РСН и вычисляют угол РСН, при котором пеленг цели равен нулю. Этот найденный угол считают УК цели, его записывают в выходной массив результатов измерений, следующее из которых получают путем вычисления новой реализации сглаженного суммарного сигнала, повторяют итерационную процедуру с новой реализацией, пока глобальные максимумы не окажутся ниже порога, после чего производится выдача потребителю массива найденных УК целей. При этом, однако, как указано и в описании [4], скорость определения УК целей с использованием компенсационного подхода меньше, чем при использовании прямоотсчетного подхода.

Недостатком аналога [4] является низкое быстродействие из-за необходимости предварительного последовательного обзора всего заданного углового сектора для получения множества реализаций сигнала, а также из-за использования зеркальной антенны, требующей применения механического привода. Хотя точность определения УК здесь выше, чем в аналоге [3], но она все же недостаточно высока из-за грубой аппроксимации нелинейной ПХ линейной функцией. Следовательно, применение его для двух плоскостей не позволит одновременно измерить две УК цели с ошибкой не более 1% ширины ДН (по уровню половинной мощности) за один импульс.

Наиболее близким по технической сущности к заявляемому способу является амплитудный моноимпульсный способ обработки сигналов при двухканальной обзорной амплитудной пеленгации [5 - патент 2225990, РФ. Способ обработки сигналов при двухканальной амплитудной пеленгации / Аветисьянц В.А., Горовой А.В., Ларионов Б.А., Музыченко Н.Ю., Фоминченко Г.Л.], принятый за прототип. В нем угловым датчиком на базе фазированной антенной решетки формируют пару ДН, раздвинутых на ширину ДН по уровню минус 3 дБ для образования РСН, осуществляют в заданном угловом секторе поиск сигналов, принимают сигналы источников радиоизлучений и селектируют их по частоте. Затем формируют ПХ углового дискриминатора путем перемещения пары ДН в пределах сектора пеленгования, вычисления абсцисс центров тяжести полученных реализаций в моменты максимальных значений корреляционных интегралов, найденных по способу совпадения полярностей, и аппроксимации ее линейной функцией, и путем решения пеленгационного уравнения вычисляют угол прихода сигналов.

Недостатками прототипа являются пониженная точность определения УК из-за недостаточно точной аппроксимации нелинейной ПХ линейной функцией, пониженная скорость измерения УК из-за необходимости получения ряда реализаций сигнала для формирования ПХ углового дискриминатора и невозможность, при использовании его для определения УК в двух плоскостях, одновременного измерения обеих УК цели с высокой точностью (1% ширины ДН по уровню половинной мощности) по одному импульсу.

Недостатком, присущим и аналогам, и прототипу заявляемого способа, является необходимость использования для одного измерения УК серии последовательных зондирующих импульсов, излучаемых в немного отличающихся направлениях. В современных условиях, при больших угловых скоростях целей, в этом случае возникает значительная ошибка определения УК, связанная с движением цели за время упомянутой серии.

Изобретений, решающих проблему влияния значений одной из измеряемых координат на процесс измерения другой координаты, авторами заявляемого способа не обнаружено.

Задачей, на решение которой направлен предлагаемый способ, является сокращение времени одновременного измерения двух УК цели при обеспечении высокой точности такого измерения и уменьшение сложности вычислителя угловых координат в обзорной амплитудной суммарно-разностной РЛС с АР и цифровой обработкой сигнала.

Для решения этой задачи предлагается способ одновременного измерения двух угловых координат цели в обзорной амплитудной моноимпульсной РЛС с АР и цифровой обработкой сигнала, при котором формируют в передатчике зондирующие импульсы, излучают их в пространство с помощью АР, формируют в соответствии с весовой функцией W(x,y), описывающей распределение поля в раскрыве АР и обеспечивающей заданный уровень боковых лепестков, диаграммы направленности парциальных каналов приема углового датчика F₁(ϑ,ϕ)≡F(ϑ-ϑ₀,ϕ), F₂(ϑ,ϕ)≡F(ϑ+ϑ₀,ϕ), F₃(ϑ,ϕ)≡F(ϑ,ϕ-ϕ₀) и F₄(ϑ,ϕ)≡F(ϑ,ϕ+ϕ₀), где ϑ, ϕ - текущие углы, отсчитываемые от РСН соответственно в азимутальной и угломестной плоскостях, проходящих через оси х, у на раскрыве АР, а ϑ₀, ϕ₀ - углы смещения максимумов упомянутых ДН от РСН, а также формируют сопряженную с ними ДН компенсационного канала, обеспечивающую определенное превышение усиления этого канала над усилением по боковым лепесткам ДН парциальных каналов, принимают отраженные от цели сигналы, осуществляют аналого-цифровое преобразование этих сигналов, на выходах парциальных каналов обнаруживают сигналы с уровнями соответственно U₁, U₂, U₃, U₄, при одновременном превышении ими уровня сигнала компенсационного канала, вычисляют сигналы рассогласования и , являющиеся значениями ПХ и углового дискриминатора для каждого из измеряемых углов, и по значениям S_CPθ, S_CPϕ находят значения УК цели ϑ_Ц и ϕ_Ц.

Согласно изобретению, в заявленном способе до приема сигналов осуществляют моделирование процесса их приема и обработки с учетом использования антенной решетки с раскрывом прямоугольной формы, при котором осуществляют факторизацию¹ (¹Представление функции двух переменных в виде произведения двух функций, каждая из которых зависит от одной переменной; это также называется разделением переменных.) двумерной весовой функции W(x,y)=W_x(х)W_y(y), исключающую при такой форме раскрыва влияние значения одной измеряемой координаты на процесс измерения другой координаты в азимутальной и угломестной плоскостях и обеспечивающую факторизацию двумерных диаграмм направленности каналов F_m(ϑ,ϕ)=F_mθ(ϑ)F_mϕ(ϕ), где - номер парциального канала приема, и зависимость двумерной пеленгационной характеристики только от измеряемой координаты , , причем одномерными весовыми функциями являются функции Хэмминга W_x(x)=0,08+0,92cos²(πx/2), -1≤х≤1 и W_y(y)=0,08+0,92cos²(πy/2), -1≤y≤1, обеспечивающие уровень боковых лепестков не выше минус 40 дБ и ширину рабочей зоны по каждой угловой координате не менее двукратной ширины ДН парциального канала по уровню половинной мощности, или другие ВФ, обеспечивающие не больший, чем функции Хэмминга, уровень боковых лепестков и не меньший размер рабочей зоны, в процессе моделирования с учетом выбранных ВФ, параметров АР и упомянутой факторизации определяют конкретный вид функций F_1ϑ(ϑ), F₂ϑ(ϑ), F_3ϕ(ϕ), и F_4ϕ(ϕ) и S_ϑ(ϑ,ϑ₀), S_ϕ(ϕ,ϕ₀), параметрически зависящих от углов смещения ϑ₀ и ϕ₀, разлагают нечетные функции S_ϑ(ϑ,ϑ₀) и S_ϕ(ϕ,ϕ₀), описывающие полученные в результате факторизации одномерные ПХ, по нечетным степеням углов ϑ и ϕ в ряды Маклорена

, ,

коэффициенты a_ϑk(ϑ₀), a_ϕk(ϕ₀) которых являются функциями углов смещения ϑ₀, ϕ₀, определяют предварительные значения этих углов смещения как результат решения задач a_ϑ3(ϑ₀)=0, a_ϕ3(ϕ₀)=0, обеспечивающих линейность пеленгационных характеристик с точностью до членов разложения пятого и более высоких порядков, затем, задавая функции , , описывающие зависимость абсолютной ошибки пеленгования от значения соответствующей координаты и угла смещения, и задавая максимальную относительную ошибку пеленгования δ_ϑmax, δ_ϕmax равной, например, 0,01 ширины диаграммы направленности, определяют функции ϑ_РЗ(ϑ₀)≡ϑ_РЗ(ϑ₀,δ_ϑmax), ϕ_РЗ(ϕ₀)≡ϕ_РЗ(ϕ₀,δ_ϕmax), описывающие зависимость размера рабочей зоны при заданной ошибке пеленгования от угла смещения и вычисляемые как минимальный по абсолютной величине корень ϑ, ϕ уравнений , соответственно, где ϑ_0.5, ϕ_0.5 - полуширина ДН по уровню половинной мощности в направлении координат ϑ, ϕ и получают окончательные значения углов ϑ₀, ϕ₀ как результат решения задач ϑ_РЗ(ϑ₀)→max, ϕ_РЗ(ϕ₀)→max, обеспечивающих максимальное значение размера рабочей зоны ϑ_РЗ(ϑ₀), ϕ_РЗ(ϕ₀) по соответствующей координате, причем внутри этой зоны абсолютная ошибка измерения углов ϑ, ϕ не превышает величины, определяемой максимальной относительной ошибкой δ_ϑmax, δ_ϕmax, вычисляют по полученным значениям углов смещения значения коэффициентов a_ϑ1(ϑ₀), a_ϕ1(ϕ₀), затем, после излучения в пространство импульсов и приема отраженных от цели сигналов, осуществляют формирование диаграмм направленности антенной решетки с учетом использованных при упомянутом моделировании весовых функций и определенных в результате моделирования значений углов смещения ϑ₀, ϕ₀, что обеспечивает линейность пеленгационных характеристик и независимость измеренных сигналов рассогласования S_CPϑ, S_CPΦ по одной угловой координате от значения другой угловой координаты, а угловые координаты цели вычисляют по формулам и , не требующим итерационного уточнения при упомянутой точности в рабочей зоне, превышающей двойную ширину диаграммы направленности парциального канала по каждой координате.

Поскольку при одновременном измерении двух УК предлагаемым способом не требуются ни повторные зондирующие импульсы, ни итерационное решение системы нелинейных уравнений (т.к. ПХ линейна на всей ширине МГЛ и не зависит от второй координаты), то сокращается время, необходимое для выполнения упомянутого измерения. Линейность ПХ, достигаемая при используемом угле разноса ДН, обеспечивает высокую точность (1% ширины ДН) измерения УК. При этом упрощается аппаратная реализация вычислителя УК за счет:

- исключения обратной связи, управляющей режимом излучения повторного импульса по результатам обработки предыдущего импульса;

- простоты вычисления УК цели путем прямого (без итераций и т.п.) решения двух независимых линейных уравнений;

- возможности независимого измерения каждой УК отдельным, более простым, комплектом аппаратуры за счет исключения влияния значения одной измеряемой координаты на процесс измерения другой координаты.

Таким образом, техническим результатом предлагаемого изобретения является сокращение времени одновременного измерения двух УК цели при высокой точности измерения (с ошибкой не более 1% ширины ДН) и уменьшение сложности вычислителя угловых координат в обзорной амплитудной суммарно-разностной РЛС с АР и цифровой обработкой сигнала.

Предлагаемое изобретение реализуется на стыке радиотехники и вычислительной математики, что соответствует современной тенденции интеграции антенной и программно-аппаратной подсистем [6 - Лучин Д.В., Юдин В.В. Конвергенция антенной и программно-аппаратной компонент как тенденция развития радиосистем диапазонов ВЧ, ОВЧ и УВЧ. // Труды НИИР / Сборник научных статей. 2014. №3. С. 73-84]. В данном случае, в частности, выявляется влияние параметров АР на эффективность вычислительной подсистемы РЛС и используются конструкторские и радиотехнические решения, обеспечивающие применение наиболее эффективных вычислительных алгоритмов.

Предлагаемое изобретение не известно в современной радиотехнике, а также не известны источники информации, содержащие сведения об аналогичных технических решениях, имеющих признаки, сходные с признаками, отличающими заявляемое решение от прототипа, а также имеющих свойства, совпадающие со свойствами заявляемого решения, поэтому можно считать, что оно обладает существенными отличиями, вытекает из них неочевидным образом и, следовательно, соответствует критериям «новизна» и «изобретательский уровень».

Сущность изобретения поясняется следующими чертежами:

фигура 1 - схема электрическая структурная системы, реализующей предлагаемый способ;

фигура 2 - а) семейство ПХ по азимуту для углов места 0°, 0.5°, 1.0°, 1.5° при ширине луча 3°, построенных для АР с круглым раскрывом (частным случаем эллиптического), б) возникновение ошибки измерения азимута при использовании ПХ для несоответствующего угла места;

фигура 3 - а) сечения ДН той же АР равноотстоящими плоскостями от максимума до угла половинной мощности, б) те же сечения после нормировки, в) увеличенный фрагмент фигуры 3б;

фигура 4 - азимутальные ПХ для сечений ДН с разными углами места относительно РСН при одинаковой ВФ: а) при эллиптическом раскрыве, б) при прямоугольном раскрыве (без обеспечения линейности ПХ).

При реализации предложенного способа выполняется следующая последовательность операций:

- до приема сигналов осуществляют моделирование процесса их приема и обработки с учетом использования АР с раскрывом прямоугольной формы и числом элементов N_x×N_y, расположенных с периодом d_x, d_y в направлении осей х, у соответственно, осуществляют факторизацию двумерной весовой функции W(x,y)=W_x(x)W_y(y), исключающую при такой форме раскрыва влияние значения одной измеряемой координаты на процесс измерения другой координаты в азимутальной и угломестной плоскостях и печивающую факторизацию двумерных ДН каналов F_m(ϑ,ϕ)=F_mθ(ϑ)F_mϕ(ϕ), где - номер парциального канала приема, а ϑ, ϕ - текущие углы, отсчитываемые от РСН соответственно в азимутальной и угломестной плоскостях, проходящих через оси x, y на раскрыве, и зависимость двумерной ПХ только от измеряемой координаты: , , где ϑ₀, ϕ₀ - углы смещения максимумов ДН от РСН, причем одномерными весовыми функциями являются функции Хэмминга W_x(х)=0,08+0,92cos²(πx/2), -1≤x≤1 и W_y(y)=0,08+0,92cos²(πy/2), -1≤y≤1, обеспечивающие уровень боковых лепестков не выше минус 40 дБ и ширину рабочей зоны по каждой УК не менее двукратной ширины ДН парциального канала по уровню половинной мощности, или другие весовые функции, обеспечивающие не больший, чем функции Хэмминга, уровень боковых лепестков и не меньший размер рабочей зоны - 1;

- определяют в процессе моделирования, учитывая выбранные ВФ, параметры АР и упомянутую факторизацию, конкретный вид парциальных ДН каналов приема и их одномерных составляющих F_1ϑ(ϑ), F_2ϑ(ϑ), F_3ϕ(ϕ), F_4ϕ(ϕ), максимумы которых смещены на углы ±ϑ₀, ±ϕ₀ от РСН, а также строят по парциальным ДН, с учетом прямоугольности раскрыва и факторизованности ВФ, модельные ПХ, зависящие только от измеряемой координаты

и параметрически зависящие от углов смещения ϑ₀ и ϕ₀ - 2;

- разлагают нечетные функции S_ϑ(ϑ,ϑ₀) и S_ϕ(ϕ,ϕ₀), описывающие полученные в результате факторизации одномерные ПХ, по нечетным степеням углов ϑ и ϕ в ряды Маклорена

коэффициенты a_ϑk(ϑ₀), a_ϕk(ϕ₀) которых являются функциями углов смещения ϑ₀, ϕ₀ осей парциальных ДН от РСН по соответствующей координате - 3;

- определяют предварительные значения углов смещения ϑ₀, ϕ₀ осей парциальных ДН как результат решения задач а_ϑ3(ϑ₀)=0, а_ϕ3(ϕ₀)=0, обеспечивающие линейность пеленгационных характеристик с точностью до членов разложения пятого и более высоких порядков - 4;

- задают аналитические функции и , описывающие зависимость абсолютной ошибки пеленгования от значения соответствующей координаты и угла смещения, а также задают максимальные относительные ошибки пеленгования δ_ϑmax, δ_ϕmax, равные, например, 0,01 ширины ДН - 5;

- определяют функции ϑ_РЗ(ϑ₀)≡ϑ_РЗ(ϑ₀,δ_ϑmax), ϕ_РЗ(ϕ₀)≡ϕ_РЗ(ϕ₀,δ_ϕmax), описывающие зависимость размера рабочей зоны при заданной ошибке пеленгования от угла смещения и вычисляемые как минимальный по абсолютной величине корень ϑ, ϕ уравнений , соответственно, где ϑ_0.5, ϕ_0.5 - полуширина ДН по уровню половинной мощности в направлении координат ϑ, ϕ - 6;

- получают окончательные значения углов ϑ₀, ϕ₀ как результат решения задач ϑ_РЗ(ϑ₀)→max, ϕ_РЗ(ϕ₀)→max, обеспечивающих максимальное значение размера рабочей зоны ϑ_РЗ(ϑ₀), ϕ_РЗ(ϕ₀) по соответствующей координате, причем внутри этой зоны абсолютная ошибка измерения углов ϑ, ϕ не превышает величины, определяемой заданной ранее максимальной относительной ошибкой δ_ϑmax, δ_ϕmax - 7;

- вычисляют по полученным значениям углов смещения значения коэффициентов a_ϑ1(ϑ₀), a_ϕ1(ϕ₀), а по используемой ВФ - значения весовых коэффициентов W_ij для каждого ij-го антенного элемента - 8;

- включают передающую и приемную части РЛС, излучают в пространство зондирующие импульсы и принимают отраженный от цели сигнал; оцифровывают принятые выходные сигналы каждого элемента АР и умножают сигнал каждого ij-го антенного элемента на коэффициент W_ij; сдвигают (возможно, путем внесения задержки) фазу ϕ_ij каждого ij-го элемента АР на величину (4 варианта), где λ - длина волны, с целью формирования четырех ДН F₁(ϑ,ϕ)≡F(ϑ-ϑ₀,ϕ), F₂(ϑ,ϕ)≡F(ϑ+ϑ₀,ϕ), F₃(ϑ,ϕ)≡F(ϑ,ϕ-ϕ₀) и F₄(ϑ,ϕ)≡F(ϑ,ϕ+ϕ₀), где ϑ, ϕ - текущие углы; суммируют сигналы элементов каналов для каждого варианта фазирования и измеряют уровень четырех сигналов U₁, U₂, U₃, U₄, принятых четырьмя парциальными ДН, оси которых разнесены на углы 2ϑ₀, 2ϕ₀ в направлении координат ϑ, ϕ соответственно; измеряют значение U_KK принятого сигнала компенсационного канала и, если измеренные для парциальных каналов величины для всех , получают значения сигналов рассогласования как и ; в противном случае считают, что в данной рабочей зоне цели отсутствуют - 9;

- вычисляют угловые координаты цели по формулам и , не требующим итерационного уточнения при упомянутой точности в рабочей зоне, превышающей двойную ширину ДН парциального канала по каждой координате - 10.

Покажем, что при этом в обзорной амплитудной суммарно-разностной РЛС с АР и цифровой обработкой сигнала достигается сокращение времени измерения двух УК цели, высокая точность измерения и уменьшение сложности вычислителя угловых координат.

При использовании комбинации двух моноимпульсных систем с общей АР, одна из которых работает в азимутальной плоскости, а вторая - в угломестной, неявно предполагается возможность независимого измерения каждой из координат цели с точностью и скоростью, соответствующими измерениям в одной плоскости. Покажем, что на самом деле в полученной таким комбинированием обзорной РЛС при высокой точности измерений УК цели в общем случае:

- проявляется зависимость результата измерений одной координаты (собственной) от значения другой (ортогональной) координаты цели относительно РСН (термины уточнены ниже),

- наличие такой зависимости вносит в измерение собственной УК методическую ошибку, ухудшающую точность измерения,

- восстановление исходной точности приводит к удлинению процесса измерения.

Для выявления названной зависимости и указанных следствий из нее рассмотрим самый простой случай измерения, когда:

- АР имеет плоский раскрыв с двумя взаимно ортогональными осями симметрии,

- формируемые лучи узкие² (²Это позволяет пренебречь различием синуса, тангенса и собственно значения угла в пределах МГЛ, а также краевыми эффектами в АР, и считать, что форма ДН не изменяется при небольших перемещениях оси ДН (в пределах двойной ширины ДН).),

- электронное сканирование (т.е. поворот МГЛ относительно раскрыва АР) не используется.

Учитывая, что время измерения в общем случае зависит от требуемой точности, максимально допустимую ошибку измерений будем считать заданной и достаточно малой (1/100 ширины ДН по уровню половинной мощности), и далее будем оценивать только время измерения, зависящее от числа зондирующих импульсов и объема вычислений.

Используем оси симметрии раскрыва как оси координат Х_ан, Y_aн на его плоскости (ось Х_ан удобно считать горизонтальной). Пусть РСН совпадает с нормалью к плоскости раскрыва, проведенной из его центра, а точечная цель находится в дальней зоне антенны в пределах МГЛ, но в стороне от РСН в пределах ширины ДН по уровню половинной мощности. Проведем картинную плоскость через цель параллельно плоскости раскрыва. На картинной плоскости через точку ее пересечения с упомянутой нормалью проведем оси координат X и Y параллельно осям Х_ан и Y_aн на раскрыве. Значение координаты точки, расположенной на оси координат, положим равным тангенсу ее углового расстояния от начала координат (при наблюдении из центра раскрыва): х=tgϑ, y=tgϕ, где ϑ=0, ϕ=0 соответствуют РСН.

Пусть оси горизонтальной (вертикальной) пары приемных лучей МГЛ разнесены на угол 2ϑ₀ (2ϕ₀) вдоль координаты х (у) и расположены в точках х_ДН=±ϑ₀, у_ДН=0 (х_ДН=0, у_ДН=±ϕ₀) картинной плоскости. Амплитуда F_пр сигнала, принятого от цели с координатами х, у, пропорциональна уровню ДН в этой точке при направлении оси ДН в точку х_ДН, у_ДН, т.е.

и зависит от обеих координат. Поэтому амплитудные суммарно-разностные ПХ, обобщенные на случай двух координат, имеют вид

и зависят от обеих координат цели и углов между осями ДН³ (³А также координат РСН, в данном случае нулевых.). Координату, вдоль которой разнесены оси пары ДН и для определения которой строится ПХ в одномерном случае, назовем собственной координатой (СК), символ этой координаты используем как нижний индекс в формулах (2) для ПХ; другую назовем ортогональной координатой (ОК).

Приравняв ПХ как известные аппаратные функции (2) и их измеренные значения S_CPΘ, S_CPϕ, получаем систему в общем случае нелинейных пеленгационных уравнений для определения координат x, y цели

где для ДН, разнесенных вдоль координаты х, соответствующей углу ϑ;

для ДН, разнесенных вдоль координаты у, соответствующей углу ϕ,

являются значениями ПХ, вычисленными по амплитудам F_Л, F_П, F_B, F_H сигналов, принятых соответственно по левому, правому, верхнему и нижнему лучам МГЛ, причем зависимость ПХ от фиксированных углов разноса лучей опущена.

Для иллюстрации особенностей измерения собственной УК в двумерном случае на фигуре 2 а изображено семейство азимутальных ПХ для РЛС с плоской многоэлементной АР с круглым раскрывом (частный случай широко используемого эллиптического раскрыва), амплитудное распределение на котором взвешено покоординатным произведением функций Хэмминга. Поскольку координата х изменяется в направлении азимута ϑ, а координата у - в направлении угла места ϕ, будем называть эти координаты азимутом и углом места (УМ) соответственно. Сечения построены для четырех углов места - от максимума ДН (главное сечение) до угла половинной мощности. Видно, что:

- ПХ нелинейны;

- ПХ для различных ОК не совпадают (зависят от значения ОК цели);

- несовпадение ПХ с различными ОК возрастает с удалением от РСН.

В этом случае для определения одной из УК цели необходимо знать значение другой УК, чтобы выбрать нужную ПХ, соответствующую цели, и наоборот. Таким образом, измерения обеих координат взаимосвязаны, что математически выражается в виде системы уравнений (3), а не двух независимых уравнений.

На фигуре 2б показано определение азимута x цели по измеренному значению S_0x=0,87 пеленгационной характеристики как графическое решение одномерного пеленгационного уравнения

S_x(x,y)=S_0x,

где у - параметр (угол места) семейства азимутальных ПХ.

Начало координат совмещено с РСН. Верхняя ПХ, соответствующая истинному УМ цели у=1,5°, дает истинное значение азимута цели х_А=1,5°. Традиционно используемая нижняя ПХ, построенная для нулевого УМ, дает ошибочное значение азимута x_B=1,7°. Отклонение 0,2° составляет 1/15 ширины ДН и многократно (в 6-7 раз) превышает максимальную ошибку известного метода [2], равную 1/100 ширины ДН по уровню половинной мощности.

Таким образом, если не учитывать различия ПХ, считая их пренебрежимо малыми, мы ограничим точность определения УК (фигура 2б) указанным отклонением; в противном случае для исключения указанной ошибки придется увеличить время и объем вычислений - например, поочередно уточняя значения одной и другой УК до тех пор, пока обе координаты в результате этих итераций не будут определены с достаточной точностью.

Отметим, что возникающая ошибка, свойственная методу измерения, является систематической; она не может быть уменьшена путем усреднения, как случайная ошибка, вносимая шумом сигнала, хотя и маскируется последней. При измерении УК цели на средней дальности (1/2-1/4 максимальной дальности действия РЛС) указанная ошибка может многократно превысить случайную ошибку, вносимую шумом⁴ (⁴Учитывая, что на максимальной дальности ошибка измерения обычно не превышает 0,1 ширины ДН, а мощность принятого сигнала обратно пропорциональна четвёртой степени расстояния до цели).

Причиной появления методической ошибки является зависимость ПХ от положения цели относительно РСН по ортогональной координате⁵ (⁵Возможная зависимость ПХ от абсолютных значений углов (например, вследствие изменения формы ДН при сканировании) здесь не рассматривается.). Если избавиться от этой зависимости и дополнительно обеспечить линейность ПХ, используя метод [2], то решение системы уравнений (3) в системе координат с началом на РСН сведется к однократному вычислению координат цели по простым формулам

использующим измеренные величины S_0x и S_0y, а также аппаратные константы а_ϑ1 и a_ϕ1 (крутизну одномерных ПХ на РСН), что обеспечит высокую скорость и точность определения угловых координат цели.

Детальный анализ показывает, что причиной зависимости ПХ от ОК является несовпадение формы нормированных одномерных ДН на сечениях с разной ОК (фиг. 3), и такая зависимость характерна для непрямоугольного раскрыва. Этот эффект проявляется как квадратичная зависимость крутизны ПХ от ОК в окрестности РСН:

где a_x=a_ϑ1, a_y=a_ϕ1,.

Поскольку ДН есть преобразование Фурье весовой функции на раскрыве антенны, то для независимости ПХ от ОК, обеспечивающей при линейной ПХ быстрый расчет без итераций по простым формулам (4), требуются:

- прямоугольная форма раскрыва;

- факторизация двумерной ВФ.

Фигура 4 иллюстрирует наличие или отсутствие зависимости ПХ от ОК для, соответственно, эллиптического или прямоугольного раскрыва при одинаковой ВФ вида W_x(t)=W_y(t)=0,3+0,7cos²(πt/2), -1≤t≤1 по каждой координате f=х, у. Положительные ветви ПХ построены для четырех сечений ДН с УМ от максимума ДН (нулевое значение угла) до угла половинной мощности (УПМ).

На фигуре 4а (эллиптический раскрыв) ПХ по азимуту зависят от УМ сечения объемной ДН⁶ (⁶Поскольку ограничение области определения факторизованной функции непрямоугольной областью нарушает факторизацию функции, рассматриваемой в неограниченной области или хотя бы внутри прямоугольника, описанного вокруг раскрыва.).

На фигуре 4б (прямоугольный раскрыв) ПХ для всех сечений совпадают, т.к. не зависят от ОК (т.е. УМ).

Для получения практически линейной ПХ (с точностью не хуже 1% ширины ДН) можно использовать одномерную ВФ Хэмминга

и угол смещения оси ДН от РСН

где λ - длина волны;

d - размер раскрыва по соответствующей координате.

При замене итерационного расчета прямым (4) происходит не менее чем трехкратное сокращение времени измерения, т.к. для оценки сходимости любого итерационного процесса требуется не менее трех итераций, а объем прямых вычислений (4) существенно меньше объема вычислений на одной итерации при решении системы (3).

Если в МГЛ попадают несколько целей, то выигрыш по времени еще больше увеличивается. Так, при обычном подходе (компенсационном или прямоотсчетном с последующим уточнением) необходимо производить итерации последовательно