Способ определения координат навигационных спутников

Способ определения координат навигационных спутников

Иллюстрации

Показать все

Реферат

Изобретение относится к способам навигации по Спутниковым Радионавигационным Системам (СРНС) и может быть использовано для определения координат навигационных спутников.

Технический результат заключается в определения координат навигационных спутников на основе измерения межспутниковых расстояний.

Известен способ определения координат навигационных спутников [Навигационный радиосигнал в диапазонах L1, L2 с открытым доступом и частотным разделением: ГЛОНАСС. Интерфейсный контрольный документ. Ред. 5.1 / Российский научно-исследовательский институт космического приборостроения. М., 2008. 74 с], который предполагает размещение на Земле группы наземных станций, осуществляющих определение координат навигационных спутников путем оптического и радиоизмерения углов и дальностей до спутников.

Наиболее близким к предлагаемому изобретению является способ [патент РФ №2508558. Система и способ оценки положения космического аппарата], состоящий в том, что система включает в себя множество принимающих станций, выполненных с возможностью принимать сигналы, переданные от космического аппарата, и обрабатывающую станцию, выполненную с возможностью принимать данные от множества принимающих станций. Каждая из принимающих станций выполнена с возможностью записывать во время временного окна, в материалах настоящей заявки указываемого ссылкой как окно записи, сигналы, переданные от космического аппарата, и передавать в обрабатывающую станцию данные, представляющие записанные сигналы во время окна записи. Окна записи, ассоциированные с каждой из принимающих станций, выполнены с возможностью быть сдвинутыми и/или иметь различный размер (т.е. различную длину или продолжительность) по отношению друг к другу. Обрабатывающая станция выполнена с возможностью коррелировать записанные сигналы для оценки для каждой по меньшей мере из одной пары среди множества принимающих станций разности расстояний между космическим аппаратом и каждой принимающей станцией из пары и на основе этого положения космического аппарата.

Недостатками данного способа определения координат являются:

- низкая точность оптических и радиоизмерений измерений, проводимых наземными станциями слежения, обусловленная влиянием атмосферных возмущений;

- необходимость размещения наземных станций для определения координат навигационных спутников и, как следствие, невозможность автономного - без наземных измерений, функционирования навигационной системы.

Заявленное изобретение направлено на решение задачи определения координат навигационных спутников на основе измерения межспутниковых расстояний.

Поставленная задача возникает при разработке систем контроля и управления навигационными спутниками, а также использования их измерений для решения навигационной задачи объекта.

Для решения задачи определения координат навигационных спутников на основе измерения межспутниковых расстояний предлагается способ, заключающийся в том, что в группе из четырех навигационных спутников, находящихся в зоне прямой видимости, состоящей из первой пары навигационных спутников, находящихся на одной орбите, и второй пары навигационных спутников, находящихся на другой орбите, реализуются одновременные измерения линейных расстояний между всеми четырьмя спутниками группы, передача от каждого спутника к каждому и прием каждым спутником от каждого результатов измерений линейных расстояний между всеми четырьмя спутниками группы, а также вычисление на каждом спутнике сферического расстояния между ним и точкой пересечения орбит, по которому определяются значения координат данного спутника.

В общем случае - при произвольном движении спутников, зная только расстояния между спутниками, определить их местоположение в пространстве невозможно. Тем не менее, учитывая существующие особенности движения навигационных спутников, а именно известность параметров их орбит и законов перемещения спутников по ним, оказывается возможным точное определение текущих координат спутников на основе измерения их взаимных дальностей. Покажем это.

Для решения этой задачи сделаем следующие допущения, адекватные практике современного использования навигационных спутников.

Разделим орбитальную сферу на две части плоскостью, проходящей через экватор, и предположим, что известна конкретная полусфера нахождения рассматриваемых спутников, движущихся по круговым орбитам.

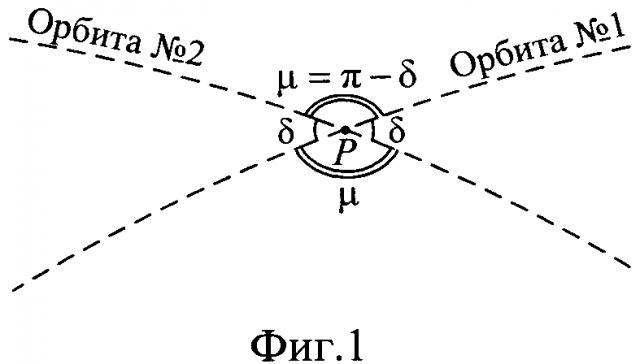
Для последующего решения рассмотрим только две орбиты №1 и №2 и обозначим точку их пересечения как Р. Пересечение рассматриваемых орбит (сферических прямых) образует на орбитальной сфере четыре сферических двухугольника с углами δ и μ=π-δ (фиг. 1).

На указанных орбитах рассмотрим следующие спутники, координаты которых необходимо определить: на орбите №1 - спутники HC₁₁ и HC₁₂, на орбите №2 - спутники HC₂₁ и HC₂₂.

Полагаем также, что спутники HC_ij, i,j=1,2 движутся по заданным круговым орбитам с одинаковым радиусом R в неизменяемом со временем порядке, однако их точное положение в пределах орбиты неизвестно.

В качестве исходных данных для определения координат навигационных спутников на основе измерения межспутниковых расстояний будем использовать следующие:

1) измеренные с высокой точностью межспутниковые дальности:

d_ij-_km - расстояния между спутниками HC_ij и HC_km; i, j, k, m=1,2;

2) известный угол δ между орбитами №1 и №2;

3) известные координаты точек пересечения орбит с экватором и углы наклонения орбит относительно экватора (или меридиана).

Для последующих построений воспользуемся основными соотношениями сферической геометрии [Основные понятия сферической геометрии и тригонометрии // Энциклопедия элементарной математики (в 5 томах). - М.: Физматгиз, 1963. - Т. 4. - С. 518-557. - 568 с.], определяя координаты спутников в географической системе координат (при необходимости пересчет в гринвичскую систему координат осуществляется по известным формулам [ГЛОНАСС. Принципы построения и функционирования. 3-е изд. / под ред. А.И. Перова, В.Н. Харисова. М.: Радиотехника, 2005. 688 с]).

Пусть спутники HC_ij, i,j=1,2, в текущий момент времени располагаются в вершинах сферического четырехугольника ABCD (фиг. 2). Направление движения спутников на фиг. 2 обозначено стрелками на пунктирных линиях, соответствующих рассматриваемым орбитам. Заметим здесь, что с учетом предварительно известных с некоторой точностью эфемерид навигационных спутников, для реализации предлагаемого ниже подхода всегда может быть осуществлен выбор тех из них, взаимное расположение которых будет соответствовать схеме, представленной на фиг. 2.

Сферические расстояния между спутниками AB, BC, CD, BD, AD и AC представляют собой длины дуг на орбитальной сфере радиуса R и могут быть определены по формулам

где σ_AB, σ_BC, σ_CD, σ_BD, σ_AD, σ_AC - соответствующие дуговые углы.

В свою очередь, дуговые углы рассчитываются по измеренным межспутниковым расстояниям и известному значению R по формуле определения угла в сферическом треугольнике с тремя известными сторонами (фиг. 3):

Предлагаемый способ определения координат навигационных спутников на основе измерения межспутниковых расстояний основан на определении сферического расстояния l от точки пересечения их орбит Р до каждого из рассматриваемых спутников, что, в свою очередь, позволяет однозначно определить местоположение всех четырех спутников в выбранной системе координат.

В качестве примера расчета спутниковых координат выберем определение координат спутника HC₁₁, движущегося по орбите №1. Для определения расстояния l рассмотрим подробнее схему расположения спутников (фиг. 4) для некоторого момента времени с отмеченным на ней искомым расстоянием.

Используя вычисленные в соответствии с (1) стороны сферических треугольников ABC и ABD, определим углы указанных треугольников по известным соотношениям [Основные понятия сферической геометрии и тригонометрии // Энциклопедия элементарной математики (в 5 томах). - М.: Физматгиз, 1963. - Т. 4. - С. 518-557. - 568 с.]:

Рассмотрим далее сферический треугольник ABP. В силу очевидных тождеств , и , все три его угла известны, и, следовательно, искомое расстояние l=AP может быть определено по теореме косинусов как

Кроме этого, легко находятся расстояния от спутников до точки пересечения орбит - BP, PC и PD:

Итак, зная расстояние l от HC₁₁ до точки пересечения орбит P (с известными координатами широты ϕ_p и долготы λ_p), рассчитаем координаты спутника HC₁₁, произведя с этой целью следующие дополнительные построения. Через точку пересечения орбит P проведем меридиан PF. Из точки расположения спутника A проведем параллель к этому меридиану AG, пересекающуюся с ним в точке G. В результате меридиан, параллель и орбита №1 образуют сферический прямоугольный треугольник APG (фиг. 5).

Тогда координаты спутника HC₁₁, расположенного в вершине A, определятся из очевидных тождеств

где ϕ_A и λ_A - широта и долгота точки A и, следовательно, искомые координаты спутника HC₁₁;

ϕ_p и λ_p - широта и долгота точки P;

и - разница значений широты и долготы точки пересечения орбит P и точки A расположения спутника (фиг. 5).

Как видно из фиг. 5, орбита №1 пересекает экватор в точке Е, а меридиан, проходящий через точку Р, - в точке F. Заметим при этом, что с учетом исходных данных решаемой задачи координаты точки Е и угол наклонения орбиты относительно экватора ∠PEF известны.

Рассмотрим далее прямоугольный сферический треугольник EPF. Длина его стороны EF определится как

где λ_F=λ_P - долгота точек F и P;

λ_E - долгота точки E.

Зная сторону EF и угол E, найдем угол ∠EPF по формуле

(Данный угол может быть вычислен заранее и задан в качестве исходных данных как угол наклонения орбиты относительно меридиана - в этом случае необходимость его вычисления на борту отсутствует).

Рассмотрим прямоугольный сферический треугольник APG. Зная сторону AP=l и угол ∠EPF, по теореме синусов найдем два возможных решения для стороны AG ( и ) по формулам

Найденной паре решений для стороны AG будут соответствовать также два решения для неизвестной стороны PG, которые по теореме косинусов определятся как

Таким образом, из (3) получаем два возможных значения координат точки A: , , , .

Определим далее конкретный вариант расположения точки A относительно точки P (вариант 1: AG₁, PG₁) или вариант 2 (вариант 2: AG₂, PG₂), исходя из того, что точка A находится на орбите №1 и отрезок орбиты от точки E до точки P является ортодромией. Воспользуемся для этого известной формулой зависимости широты ϕ от долготы λ точки, находящейся на ортодромии между двумя точками с известными координатами (в данном случае между точками E и P) [Дмитриев В.И. Навигация и лоция. - М.: МОРКНИГА, 2009. 458 с.]

Тогда, подставляя в формулу (4) вместо λ полученные решения λ_A1 и λ_A2, получим два соответствующих значения широты точки A - ϕ'_A1 и ϕ'_A2. Сравнивая полученные значения ϕ'_A1 и ϕ'_A2 с рассчитанными ранее значениями ϕ_A1 и ϕ_A2, в качестве окончательного решения выбираем вариант, отвечающий условию нахождения точки А на орбите №1 на заданном расстоянии l от точки P, т.е. вариант i, для которого , i=1,2.

Координаты остальных спутников определяются на основе расстояний от них до точки пересечения орбит (т.е. на основе расстояний BP, PC и PD) аналогично рассмотренному выше алгоритму их определения для спутника HC₁₁.

Таким образом, предлагаемый алгоритм идентификации эфемерид навигационных спутников можно представить в виде следующих последовательных этапов.

На этапе 1 реализуются одновременные измерения линейных расстояний между всеми четырьмя спутниками группы HC₁₁, HC₁₂, HC₂₁ и HC₂₂, находящимися на орбитах 1 и 2.

На этапе 2 реализуются передача от каждого спутника к каждому и прием каждым спутником от каждого результатов измерений расстояний между всеми четырьмя спутниками группы - HC₁₁, HC₁₂, HC₂₁ и HC₂₂.

На этапе 3 на основе измеренных и принятых межспутниковых дальностей в каждом спутнике вычисляются расстояния l_i между спутниками и точкой пересечения орбит в соответствии с выражением (2).

На этапе 4 по вычисленным расстояниям l_i определяются значения координат всех спутников в географической (или гринвичской - путем дополнительного перерасчета) системе координат.

Предложенный способ определения координат навигационных спутников на основе измерения межспутниковых расстояний позволяет определять их текущие координаты непосредственно на борту спутников, снижая тем самым вычислительную нагрузку на приемники потребителей и телеметрических станций слежения, и повысить автономность спутниковой группировки, используя простые методы радио- и лазерных измерений, позволяющие увеличить точность определения спутниковых координат в силу большей точности межспутниковых измерений, осуществляемых в космосе, по сравнению с телеметрическими, подверженными влиянию атмосферных возмущений.

Способ определения координат навигационных спутников на основе измерения межспутниковых расстояний, заключающийся в том, что в группе из четырех навигационных спутников, находящихся в зоне прямой видимости, состоящей из первой пары навигационных спутников, находящихся на одной орбите, и второй пары навигационных спутников, находящихся на другой орбите, реализуются одновременные измерения линейных расстояний между всеми четырьмя спутниками группы, передача от каждого спутника к каждому и прием каждым спутником от каждого результатов измерений линейных расстояний между всеми четырьмя спутниками группы, а также вычисление на каждом спутнике сферического расстояния между ним и точкой пересечения орбит, по которому определяются значения координат данного спутника.