Способ определения аэродинамического нагрева высокоскоростного летательного аппарата в опережающих лётных исследованиях на крупномасштабной модели

Способ определения аэродинамического нагрева высокоскоростного летательного аппарата в опережающих лётных исследованиях на крупномасштабной модели

Иллюстрации

Показать все

Реферат

Область техники

Изобретение относится к области авиационно-космической техники и технологии, а именно к способам определения аэродинамического нагрева высокоскоростного летательного аппарата (далее натуры) в опережающих летных исследованиях на крупномасштабной модели (далее модели) и может быть использовано для теплового проектирования натуры по данным ее аэродинамического нагрева. Определение аэродинамического нагрева натуры, необходимого для ее теплового проектирования, по известному из опережающих летных исследований аэродинамическому нагреву модели осуществляют из условия подобия распределений температуры в материалах теплозащиты модели и натуры.

Уровень техники

Известен способ применения теории подобия для краевых задач нестационарной теплопроводности, рассмотренный в книге «Приближенные решения нелинейных задач теплопроводности» (Л.И. Кудряшев, Н.Л. Меньших, М.: Машиностроение, 1979). Для выяснения необходимых условий подобия в краевой задаче нестационарной теплопроводности, включающей в себя дифференциальное уравнение переноса тепла в теле заданной геометрической формы с начальным и граничным (учитывающим аэродинамический нагрев и излучение радиацией) условиями, выполняют некоторые линейные преобразования, которые позволяют получить формулировку задачи в безразмерном виде. Анализ безразмерного вида краевой задачи позволяет сделать вывод о том, что температурные поля в телах заданной геометрической формы будут подобными, если эти тела будут геометрически подобны, а также, если числа подобия, полученные в результате применения линейных преобразований, будут равны. Для краевой задачи нестационарной теплопроводности без внутренних источников теплоты такими числами подобия будут числа Био, Больцмана, Фурье и безразмерная температура.

Основным недостатком применения данного способа при определении аэродинамического нагрева натуры в опережающих летных исследованиях на модели является отсутствие при задании этого нагрева в граничном условии краевой задачи нестационарной теплопроводности зависимости числа подобия Био от числа подобия Нуссельта, являющегося функцией чисел подобия Маха, Прандтля, Рейнольдса, безразмерных температуры и вязкости.

Известен способ определения температуры и теплового потока на поверхности тела по данным температурных измерений в нем, рассмотренный в книге «Обратные задачи теплообмена» (О.М. Алифанов, М.: Машиностроение, 1988). Способ определения указанных характеристик на поверхности исследуемого тела основан на решении соответствующих интегральных уравнений путем итерационной минимизации квадратичного функционала невязки расчетной и измеренной в отдельных точках внутри тела с помощью термопар температур. Минимизацию квадратичного функционала невязки обычно осуществляют методом сопряженных градиентов с остановом итерационного процесса по номеру итерации, согласованному с погрешностью измерения температуры в теле. Проведенные расчеты показывают, что при этом можно обеспечить точность восстановления температуры и тепловых потоков на поверхности тела, соизмеримую с точностью температурных измерений в нем.

Основными недостатками данного способа являются отсутствие опыта его применения в летном эксперименте, а также некоторая сложность установки термопар в исследуемом теле.

Наиболее близким способом, принятым за прототип, по совокупности признаков, является способ проведения аэротермодинамических исследований на летающих моделях в интересах создания многоразового воздушно-космического корабля «Буран», рассмотренный в книге «Жаростойкие и теплозащитные конструкции многоразовых аэрокосмических аппаратов» (В.Я. Гофин, Москва Мир, 2003). Реализация способа включала определение высоты и скорости полета модели, теплопроводности, объемной теплоемкости и степени черноты материала ее теплозащиты, проведение опережающих летных исследований на модели с измерениями температуры и кондуктивного теплового потока, а также определением аэродинамического теплового потока на ее наружной поверхности. Значения высоты и скорости полета летающей модели «Бор-5», представляющей собой в масштабе 1:8 копию «Бурана», определялись из равенств для модели и «Бурана» чисел подобия Маха и Рейнольдса. Величины теплопроводности, объемной теплоемкости и степени черноты материала теплозащиты модели выбирались, в основном, из соображений работоспособности материала теплозащиты в условиях более высокой, по сравнению с «Бураном», температуры наружной поверхности модели.

Опережающие летные исследования на модели «Бор-5» проводили следующим образом. Модель выводилась на суборбиту ракетой-носителем, после чего разделялась с ней и продолжала автономный полет по баллистической траектории. Далее модель входила в верхние слои атмосферы и выполняла исследовательскую программу. По завершении исследовательского участка траектории ее полета в атмосфере бортовая система управления переводила модель в крутую спираль для уменьшения скорости полета, после чего выпускался парашют, на котором она приземлялась. Значения температуры и кондуктивного теплового потока на наружной поверхности модели «Бор-5» на исследовательском участке траектории ее полета непосредственно измерялись с помощью термопар и калориметрических датчиков, соответственно.

Основным недостатком применения данного способа при определении аэродинамического нагрева натуры в опережающих летных исследованиях на модели является использование ограниченного набора чисел подобия, что в итоге приводит к невозможности определения этого нагрева. Другим недостатком применения этого способа является высокая погрешность определения температуры и кондуктивного теплового потока на наружной поверхности модели, при их непосредственном измерении термопарами и калориметрическими датчиками, соответственно.

Раскрытие изобретения

Технический результат, на достижение которого направлено предлагаемое изобретение, заключается в повышении точности определения аэродинамического нагрева натуры в опережающих летных исследованиях на модели.

Для достижения указанного технического результата в предлагаемом способе определения аэродинамического нагрева натуры в опережающих летных исследованиях на модели, в отличие от известного, высоту и скорость полета модели, теплопроводность, объемную теплоемкость и степень черноты материала ее теплозащиты, а также аэродинамический тепловой поток на наружной поверхности натуры в сходственных с моделью точках определяют из условия подобия в этих точках распределений температуры в материалах теплозащиты модели и натуры по координате y_i и времени полета τ. При этом температуру и кондуктивный тепловой поток на наружной поверхности модели определяют из решения соответствующих интегральных уравнений по измеренным в материале теплозащиты с помощью термопар температурам, для чего вводят в рассмотрение изобарическую теплоемкость с_р и показатель адиабаты κ воздушного потока, характерный наружный размер l, характерную толщину теплозащиты δ, высоту h=h(τ) и скорость V_h=V_h(τ) полета, статические температуру T_h=T(h) и давление p_h=p(h), а также динамическую вязкость μ_0h=μ(T_0h) при температуре торможения воздушного потока на высоте полета, теплопроводность и динамическую вязкость воздушного потока при температуре наружной поверхности , теплопроводность λ=λ(τ), объемную теплоемкость С=С(τ) и степень черноты ε=ε(τ) материала теплозащиты, аэродинамический тепловой поток на наружной поверхности, коэффициент излучения абсолютно черного тела σ; задают числа подобия Био , Нуссельта , Маха , Прандтля , Рейнольдса , безразмерные температуру и вязкость , Больцмана и Фурье , изобарическую теплоемкость воздушного потока с_р=1005Дж/(кг⋅К), характерные наружные размеры натуры l_Н и модели l_М, характерные толщины теплозащиты натуры δ_Н и модели δ_М, высоту h_H=h_H(τ) и скорость V_hH=V_hH(τ) полета натуры, теплопроводность λ_Н=λ_Н(τ), объемную теплоемкость С_Н=С_Н(τ) и степень черноты ε_Н=ε_Н(τ) материала теплозащиты натуры, затем, используя эти данные, последовательно определяют:

- высоту полета модели h_M=h_M(τ) из решения уравнения, полученного из равенств для модели и натуры чисел Маха, Рейнольдса, безразмерных температуры и вязкости:

где Т_hH=T(h_M), р_hH=p(h_M) - статические температура и давление воздушного потока на высоте полета модели, соответственно; T_hH=T(h_H), p_hH=p(h_H) - статические температура и давление воздушного потока на высоте полета натуры, соответственно; - безразмерная динамическая вязкость при температурах торможения и воздушного потока на высотах полета модели и натуры, соответственно;

- скорость полета модели V_hM=V_hM(τ), полученную из равенства для модели и натуры числа Маха:

- теплопроводность материала теплозащиты модели λ_М=λ_М(τ), полученную из равенств для модели и натуры чисел Био, Нуссельта, Прандтля и безразмерной вязкости:

- объемную теплоемкость материала теплозащиты модели С_М=С_М(τ), полученную из равенства для модели и натуры числа Фурье:

- степень черноты материала теплозащиты модели ε_М=ε_М(τ), полученную из равенств для модели и натуры чисел Больцмана и Маха:

Далее задают начальное распределение температуры и координаты точек установки и термопар в материале теплозащиты модели; устанавливают в этих точках термопары; затем проводят опережающие летные исследования на модели, во время которых с помощью установленных термопар измеряют температуры и , а после проведения испытаний, используя эти данные, последовательно определяют:

- температуру на наружной поверхности модели из решения интегрального уравнения:

где и - функции Грина первой краевой задачи теплопроводности;

- кондуктивный тепловой поток на наружной поверхности модели из решения интегрального уравнения:

где , и - функции Грина смешанной краевой задачи теплопроводности;

- аэродинамический тепловой поток на наружной поверхности модели, полученный из условия теплового баланса:

где σ=5,67⋅10^-8 Вт/(м²⋅К⁴) - коэффициент излучения абсолютно черного тела;

- аэродинамический тепловой поток на наружной поверхности натуры, полученный из равенств для модели и натуры чисел Био, Маха и безразмерной температуры:

Таким образом, точность определения аэродинамического теплового потока на наружной поверхности натуры достигается за счет того, что высоту и скорость полета модели, теплопроводность, объемную теплоемкость и степень черноты материала ее теплозащиты, а также данный тепловой поток определяют из равенств для модели и натуры чисел подобия Био (в зависимости от числа подобия Нуссельта, являющегося функцией чисел подобия Маха, Прандтля, Рейнольдса, безразмерных температуры и вязкости), Больцмана, Фурье и безразмерной температуры, а также за счет того, что температуру и кондуктивный тепловой поток на наружной поверхности модели определяют из решения соответствующих интегральных уравнений по измеренным в материале теплозащиты с помощью термопар температурам.

Предлагаемое изобретение иллюстрируется чертежами, на которых изображены:

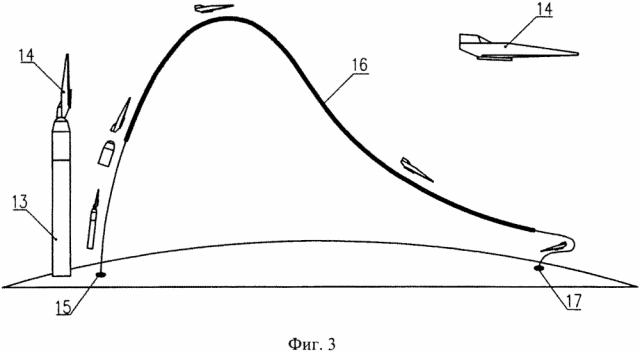
на фиг. 1 показаны рассчитанные для модели, а также заданные для натуры высота и скорость полета по времени;

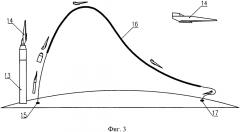
на фиг. 2 показан вариант установки термопар в материале теплозащиты модели;

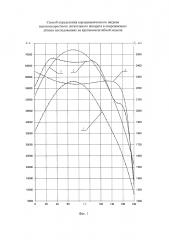
на фиг. 3 показана схема проведения опережающих летных исследований на модели;

на фиг. 4 показаны измеренные в материале теплозащиты модели температуры, а также рассчитанная на ее наружной поверхности температура по времени полета;

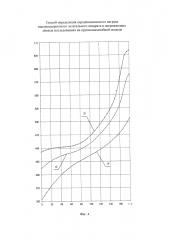
на фиг. 5 показаны рассчитанные на наружной поверхности модели кондуктивный и аэродинамический тепловые потоки, а также рассчитанный на наружной поверхности натуры аэродинамический тепловой поток и заданный для сравнения с ним «эталонный» тепловой поток по времени полета.

Предлагаемый способ осуществляют следующим образом

Высоту и скорость полета модели, теплопроводность, объемную теплоемкость и степень черноты материала ее теплозащиты, а также аэродинамический тепловой поток на наружной поверхности натуры в сходственных с моделью точках определяют из условия подобия в этих точках распределений температуры в материалах теплозащиты модели и натуры по координате y_i и времени полета τ. При этом температуру и кондуктивный тепловой поток на наружной поверхности модели определяют из решения соответствующих интегральных уравнений по измеренным в материале теплозащиты с помощью термопар температурам, для чего задают числа подобия Био (в зависимости от числа подобия Нуссельта, являющегося функцией чисел подобия Маха, Прандтля, Рейнольдса, безразмерных температуры и вязкости), Больцмана, Фурье и безразмерную температуру, изобарическую теплоемкость воздушного потока с_р=1005Дж/(кг⋅К), характерные наружные размеры натуры l_Н и модели l_М, характерные толщины теплозащиты натуры δ_H и модели δ_M, высоту h_H=h_H(τ) и скорость V_hH=V_hH(τ) полета натуры, теплопроводность λ_Н=λ_Н(τ), объемную теплоемкость С_Н=С_Н(τ) и степень черноты ε_Н=ε_Н(τ) материала теплозащиты натуры, затем, используя эти данные, последовательно определяют: высоту h_M=h_M(τ) и скорость V_hM=V_hM(τ) полета модели по формулам (1) и (2), соответственно; теплопроводность λ_M=λ_M(τ), объемную теплоемкость С_М=С_М(τ) и степень черноты ε_M=ε_М(τ) материала ее теплозащиты по формулам (3)÷(5), соответственно.

Далее задают начальное распределение температуры и координаты точек установки и термопар в материале теплозащиты модели; устанавливают, как показано на фиг. 2, в этих точках термопары; затем, в соответствии с фиг. 3, проводят опережающие летные исследования на модели, во время которых с помощью установленных термопар измеряют температуры и , а после проведения испытаний, используя эти данные, последовательно определяют: температуру и кондуктивный тепловой поток на наружной поверхности модели по формулам (6) и (7), соответственно; аэродинамические тепловые потоки и на наружных поверхностях модели и натуры по формулам (8) и (9), соответственно.

Пример

С целью проверки работоспособности и точности предлагаемого способа определения аэродинамического нагрева натуры в опережающих летных исследованиях на модели, по формулам (1)÷(9), был проведен контрольный расчет аэродинамического теплового потока на наружной поверхности носка натуры в области полного торможения воздушного потока в , N=1 сходственной с моделью точке.

Необходимые для расчета значения задаваемых величин были следующими: характерные наружные размеры натуры lн=33 м и модели l_М=4,4 м, характерные толщины теплозащиты натуры δ_Н=2⋅10^-2 м и модели δ_M=10^-2 м, теплопроводность λ_Н=λ_Н(τ)=10 Вт/(м⋅К), объемная теплоемкость С_Н=С_Н(τ)=3,5⋅10⁶ Дж/(м³⋅К) и степень черноты ε_Н=ε_Н(τ)=0,2 материала теплозащиты натуры, начальное распределение температуры в материале теплозащиты модели изменялось в пределах .

Безразмерная динамическая вязкость при температурах торможения воздушного потока на высотах полета модели и натуры при равенстве числа Маха задавалась по формуле Саттерлэнда , в которой постоянная температура принималась равной T_s=110 К.

На фиг. 1 показаны рассчитанные по формулам (1) и (2) высота h_M=h_M(τ) 1 и скорость V_hH=V_hM(τ) 2 полета модели, соответственно, а также заданные высота h_H=h_H(τ) 3 и скорость V_hH=V_hH(τ) 4 полета натуры по времени τ. Момент времени τ=0 соответствует моменту отделения модели и натуры от своих ракет-носителей и началу их автономного полета в атмосфере. Для модели это время является также началом исследовательского участка траектории ее полета в атмосфере.

Рассчитанные по формулам (3)÷(5) теплопроводность, объемная теплоемкость и степень черноты материала теплозащиты модели достаточно слабо изменяются по времени полета и, в целом, имеют следующие значения: теплопроводность λ_M=λ_M(τ)=40 Вт/(м⋅К), объемная теплоемкость С_M=С_M(τ)=5,5⋅10⁷ Дж/(м³⋅К) и степень черноты ε_M=ε_M(τ)=0,93.

На фиг. 2 показан вариант установки термопар в материале теплозащиты модели. Сваренную «встык» термопару 5 со специальным покрытием, препятствующим ее шунтированию, укладывают в пазы 6, сделанные на боковой и торцевой поверхностях цилиндрической вставки 7. Для установки термопар в материал теплозащиты 8 в точки 9, находящиеся на расстояниях =2⋅10^-3 м и =δ_M от наружной поверхности 10, изготавливают вставки различной высоты, которые запрессовывают с внутренней поверхности 11 в соответствующие по глубине глухие отверстия 12.

На фиг. 3 показана схема проведения опережающих летных исследований на модели. Ракета-носитель 13 с установленной на ней моделью 14 вертикально стартует с земной поверхности 15 и разгоняет модель в атмосфере до заданных высот и скоростей полета, после чего разделяется с ней. Далее модель совершает автономный полет на исследовательском участке 16 траектории ее полета в атмосфере. После прохождения исследовательского участка модель переходит в режим предпосадочного маневра и по его завершении осуществляет посадку на взлетно-посадочную полосу 17.

На фиг. 4 показаны измеренные в материале теплозащиты модели температуры 18 и 19, а также рассчитанная на ее наружной поверхности по формуле (6) температура 20 по времени τ. В качестве измеренных температур и были приняты соответствующие расчетные значения этих температур, найденные из решения краевой задачи теплопроводности для модели.

На фиг. 5 показаны рассчитанные на наружной поверхности модели по формулам (7) и (8) кондуктивный 21 и аэродинамический 22 тепловые потоки, соответственно, а также рассчитанный на наружной поверхности натуры по формуле (9) аэродинамический тепловой поток 23 по времени τ. Для оценки точности предлагаемого способа рассчитанный аэродинамический тепловой поток сравнивают с заданным «эталонным» тепловым потоком 24, полученными из решения краевой задачи теплопроводности для натуры. Из сравнения видно, что максимальная погрешность определения аэродинамического теплового потока на наружной поверхности натуры предлагаемым способом составляет менее 3%, что доказывает его высокую работоспособность и точность.

Способ определения аэродинамического нагрева высокоскоростного летательного аппарата (далее натуры) в опережающих летных исследованиях на крупномасштабной модели (далее модели), включающий определение высоты и скорости полета модели, теплопроводности, объемной теплоемкости и степени черноты материала ее теплозащиты, проведение опережающих летных исследований на модели с измерениями температуры и кондуктивного теплового потока, а также определением аэродинамического теплового потока на ее наружной поверхности, отличающийся тем, что высоту и скорость полета модели, теплопроводность, объемную теплоемкость и степень черноты материала ее теплозащиты, а также аэродинамический тепловой поток на наружной поверхности натуры в сходственных с моделью точках определяют из условия подобия в этих точках распределений температуры в материалах теплозащиты модели и натуры по координате yⁱ и времени полета τ, при этом температуру и кондуктивный тепловой поток на наружной поверхности модели определяют из решения соответствующих интегральных уравнений по измеренным в материале теплозащиты с помощью термопар температурам, для чего задают числа подобия Био (в зависимости от числа подобия Нуссельта, являющегося функцией чисел подобия Маха, Прандтля, Рейнольдса, безразмерных температуры и вязкости), Больцмана, Фурье и безразмерную температуру, изобарическую теплоемкость воздушного потока с_р=1005 Дж/(кг⋅К), характерные наружные размеры натуры и модели , характерные толщины теплозащиты натуры δ_H и модели δ_M, высоту h_H=h_H(τ) и скорость V_hH=V_hH(τ) полета натуры, теплопроводность λ_H=λ_H(τ), объемную теплоемкость C_H=C_H(τ) и степень черноты ε_H=ε_H(τ) материала теплозащиты натуры, затем, используя эти данные, последовательно определяют:

- высоту полета модели h_M=h_M(τ) из решения уравнения, полученного из равенств для модели и натуры чисел Маха, Рейнольдса, безразмерных температуры и вязкости

где T_hM=T(h_M), p_hM=p(h_M) - статические температура и давление воздушного потока на высоте полета модели, соответственно; T_hH=T(h_H), p_hH=p(h_H) - статические температура и давление воздушного потока на высоте полета натуры соответственно; - безразмерная динамическая вязкость при температурах торможения и воздушного потока на высотах полета модели и натуры соответственно;

- скорость полета модели V_hM=V_hM(τ), полученную из равенства для модели и натуры числа Маха

- теплопроводность материала теплозащиты модели λ_M=λ_M(τ), полученную из равенств для модели и натуры чисел Био, Нуссельта, Прандтля и безразмерной вязкости

- объемную теплоемкость материала теплозащиты модели C_M=C_M(τ), полученную из равенства для модели и натуры числа Фурье

- степень черноты материала теплозащиты модели ε_M=ε_M(τ), полученную из равенств для модели и натуры чисел Больцмана и Маха

далее задают начальное распределение температуры и координаты точек установки и термопар в материале теплозащиты модели; устанавливают в этих точках термопары; затем проводят опережающие летные исследования на модели, во время которых с помощью установленных термопар измеряют температуры и , а после проведения испытаний, используя эти данные, последовательно определяют:

- температуру на наружной поверхности модели из решения интегрального уравнения

где и - функции Грина первой краевой задачи теплопроводности;

- кондуктивный тепловой поток на наружной поверхности модели из решения интегрального уравнения

где , и - функции Грина смешанной краевой задачи теплопроводности;

- аэродинамический тепловой поток на наружной поверхности модели, полученный из условия теплового баланса

где σ=5,67⋅10^-8 Вт/(м²⋅К⁴) - коэффициент излучения абсолютно черного тела;

- аэродинамический тепловой поток на наружной поверхности натуры, полученный из равенств для модели и натуры чисел Био, Маха и безразмерной температуры