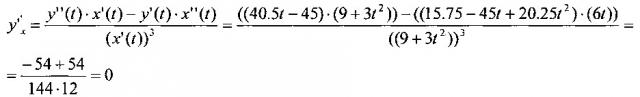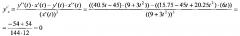Способ имитации траекторий движения объектов

Способ имитации траекторий движения объектов

Иллюстрации

Показать все

Реферат

Изобретение относится к локационной технике и может быть использовано в тренажерах подготовки операторов локационных станции для воспроизведения траекторий, а также для функционально-диагностического контроля локационных систем.

Известен способ описания кривой Безье, задаваемой графически и аналитически с наглядным, интуитивным представлением отдельных сегментов ее воспроизведения, с гибкой, постепенной деформацией формы и кривизны [1]. Обеспечено параметрическое задание уравнений кривой по прямоугольным координатам в функции безразмерного параметра t∈[0; 1]. Но способ задает материальными средствами лишь геометрическую форму кривой и не обеспечивает материальными средствами физическое воспроизведение траектории движения воздушного объекта с учетом его кинематики - скоростей, ускорений, непосредственно привязанных к каждой точке всей траектории в заданные моменты времени. Безразмерный параметр t∈[0; 1] не привязан к реальному времени t_p движения по траектории. Не обеспечен контроль и корректировка динамических параметров движения в виде перегрузок, превышающих заданные предельные значения, например для летчика больше 8-ми ускорений свободного падения g=9.8 м/c². Не реализовано комплексирование сложной траектории из сегментов, состоящей из разнообразных сопрягаемых участков, например, в виде отрезков прямых, у которых радиус кривизны равен бесконечности, и кривых с конечными значениями радиуса кривизны.

Известен способ имитации траекторий движения воздушных объектов [2-5], состоящий в ручном вводе координат опорных точек, образующих очерчивающую траекторию движения - ломаную линию, с указанием скоростей полета в этих точках при последовательном (по мере ввода) накоплении массива информации об опорных точках, автоматическим расчетом уравнений движения по трем координатами x(t_p), y(t_p), z(t_p) и скорости V(t) вдоль прямолинейных курсов и переходных кривых с плавным изменением радиуса кривизны R_k, образованных чередующимися круговыми и параболическими сегментами, в режиме задания траектории. В режиме расчета положения объекта вычисленные параметры законов движения извлекаются из памяти и используются в качестве операндов при определении его положения на траектории путем подстановки в рассчитанный закон движения текущего значения времени t_p, периодически поступающего с таймера в качестве внешнего сигнала на запрос координат объекта.

Известному способу, являющемуся прототипом изобретения, присущи недостатки. Процесс формирования траектории не обладает наглядным, интуитивным представлением задания сложных вариантов ее воспроизведения с гибкой, постепенной деформацией формы и кривизны. Траектория движения объекта образуется только набором чередующихся круговых, параболических и прямолинейных сегментов. Траектория обладает нулевым кручением и, таким образом, более адаптирована для имитации плоских маневров воздушного объекта. Движение вдоль каждого сегмента тривиально: в общем случае оно является равноускоренным, как вариант - равномерным. Оператор лишен возможности решающим образом определять скоростной режим движения объекта вдоль траектории: способ допускает задание только мгновенной скорости в каждой узловой точке опорной ломаной линии, которая интерпретируется методом как скорость в точке выхода объекта на переходную кривую, сглаживающую траекторию вблизи соответствующей точки, каждая переходная кривая имеет ось симметрии. Обеспечено точное аналитическое воспроизведение траектории в параметрической функции времени только для сегментов в виде отрезков прямых и дуг окружностей. Итак, в целом ограничены возможности большей адекватности траектории движения виртуальной воздушной цели по отношению к ее реальному прототипу.

Целью изобретения является расширение функциональных возможностей способа имитации траекторий движения воздушных объектов с расчетом на создание более адекватной трассы полета в трехмерном пространстве без скачков скоростей и ускорений путем наглядного формирования более реалистичной трассы полета в трехмерном воздушном пространстве при произвольном характере изменения скорости в каждый момент времени. Это обеспечивает повышение качества подготовки операторов, более эффективный функционально-диагностический контроль аппаратуры локационных станций. Поставленная цель достигается тем, что предлагается использовать более эффективный метод сегментации траекторий - на основе гладко совмещенных кривых различных степеней, построенных на общей опорной ломаной, которая определена группой из последовательно расположенных сегментов. Для полученных кинематических параметров движения по заданной траектории предписан и скоростной режим движения таким образом, чтобы определить текущую точку на трассе, в которой будет находиться объект в произвольный момент времени. С этой целью параллельно с траекторией задаются и уравнения скорости V(t_p) на основе ее значений в узловых точках и соответствующих производных, представляющих ускорения. Для связывания между собой геометрии (кусочно-заданной кривой) и кинематики (профиль скорости) движения используется объединяющий их параметр - пройденный путь S, предусмотрена возможность контроля скорости, тангенциального ускорения и общей переносимой перегрузки в каждой точке пути.

Для достижения технического результата в заявляемом способе положение и геометрическое представление траектории движения объекта в пространстве плавно комплексируется из последовательно сопрягаемых сегментов с итерационными, наглядными графическими интуитивными изменениями их формы и кривизны, расчетом параметрических уравнений движения в каждом сегменте по трем координатам x(t), y(t), z(t) зоны обзора радиолокационной станции в функции безразмерного параметра t∈[0; 1] с преобразованием его при различных законах изменений линейной скорости движения в функцию от аргумента - линейно-нарастающего временного интервала реального времени t_p воспроизведения траектории путем определения проходимого по сегментам пути S(t_p), вычисления в соответствии с обратной функцией значений t(S) в каждом сегменте и последующим вычислением в блоке расчета координат по параметрическим уравнениям движения значений текущих декартовых координат объекта.

Способ также отличается тем, что:

1) геометрическая форма каждого сегмента общей траектории движения гибко, интуитивно выстраивается на основе итерационного изменения расположения координат n опорных точек ({P_i}={x_i, y_i, z_i}, i=0, …, n-1) опорной ломаной линии кривой Безье сегмента с n узлами, автоматическим расчетом параметрических уравнений движения в каждом сегменте по трем координатам x(t), y(t), z(t) зоны обзора радиолокационной станции в функции безразмерного параметра t∈[0; 1], по параметрическим уравнениям определяется максимальный путь по сегменту S_max - длина сегмента, минимальный радиус кривизны, обеспечивающий проверку и исключение критических перегрузок при максимальных линейных скоростях движения;

2) переход с одного сегмента кривой Безье на другой производится с плавным изменением радиуса кривизны, обеспечением непрерывности первой и второй производных двух сопрягаемых кривых, когда для сопрягаемых сегментов из кубической параболы и отрезка прямой или двух кубических парабол соответственно их пять смежных вершин лежат на одной прямой или составляют выпуклый многоугольник;

3) в соответствии с параметрическими уравнениями каждого сегмента в функции безразмерного параметра t вычисляется путь, пройденный по параметрически заданной кубической кривой в функции S(t), воспроизводится обратная функция t(S) с последующей аппроксимацией ее полиномом наилучшего приближения g(S),

по заданному закону воспроизведения скорости на заданном сегменте определяются текущее значение пройденного пути S(t_p1) в функции текущего временного интервала t_p1 от начала сегмента и времени движения по сегменту, время прохождения сегмента,

по общему, связывающему параметру текущего пути S на сегменте осуществляется переход от времени t_p1 к параметру t с последующей подстановкой его в параметрические уравнения вычисления прямоугольных координат;

4) предварительные действия оператора, направленные на проектирование модели движения, подготовительные расчеты обеспечивают в общем временном интервале формирования траектории движения определение моментов времени начала, продолжительности и окончания движения объекта по каждому сегменту, которые позволяют идентифицировать именно тот сегмент, по которому перемещается объект в момент времени t_p воспроизведения каждого сегмента, с присвоением ему порядкового номера,

к каждому порядковому номеру сегмента привязывается таблица уравнений движения на заданном сегменте;

5) при формообразовании обрабатываемых деталей геометрическая форма траектории движения рабочего органа привязывается к системе координат робототехнического комплекса или станка с числовым программным управлением, а скоростной режим движения определяется их динамическими характеристиками.

Предлагаемый способ имитации траекторий иллюстрируется чертежами, представленными на фиг. 1-8: фиг. 1 - сопряжение кривой Безье 3-й степени с отрезком прямой линии, фиг. 2 - график для определения минимального радиуса кривизны, фиг. 3 - аппроксимация полиномом 2-й степени пути S(t), фиг. 4 - аппроксимация полиномом 3-й степени пути S(t), фиг. 5 - аппроксимация полиномом 2-й степени обратной функции t(S), фиг. 6 - аппроксимация полиномом 3-й степени обратной функции t(S), фиг. 7 - график погрешности полинома g(t)=0.436+10.614⋅t+0,916⋅t², фиг. 8 - график погрешности полинома g(t)=0.095+16.116⋅t-12.862⋅t²+8.896⋅t³.

Как и в прототипе, способ сочетает в себе предварительные действия оператора, направленные на проектирование модели движения, подготовительные расчеты, необходимые для определения траекторий движения, а также расчеты, вычисляющие мгновенные значения координат движущегося объекта в реальном масштабе времени. Эти процессы можно представить исходя из обоснования моделей воспроизведения траекторий.

Математические модели воспроизведения траекторий движения. Определение геометрии трассы движения объекта. Уравнения для воспроизведения геометрической формы кривой.

Параметрическое представление кривой Безье имеет вид:

где n - степень кривой; i - порядковый номер опорной вершины; P_i - вектор координат i-й опорной точки; - полином Бернштейна степени n, t - безразмерный параметр, расположенный в интервале t∈[0; 1].

В качестве траектории движения объекта зададим кусочно-заданную пространственную кривую, состоящую из плавно совмещаемых сегментов, например, в виде кривых Безье (1) преимущественно первого, второго и третьего порядков. Совокупность такого набора сегментов позволяет представить прямолинейные участки траектории, участки с ненулевой кривизной, участки с ненулевой кривизной и ненулевым кручением - и таким образом описать различные виды маневра воздушного объекта. Использование кривой Безье более высокого порядка, чем 3-й, в составе траектории существенно не развивает ее свойства, но усложняет аналитические выражения для расчета мгновенных координат движущегося объекта. Геометрическая форма каждого сегмента общей траектории движения выстраивается на основе расположения n опорных точек ({P_i)}={x_i, y_i, z_i}, i=0, …, n-1), т.е. опорной ломаной линии с n узлами.

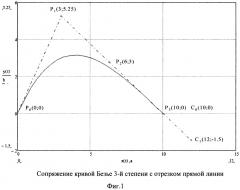
Конкретное расположение смежных точек стыка на отдельных сопрягаемых сегментах необходимо выбрать таким образом, чтобы получить в целом гладкую и гибкую пространственную траекторию, управляемую точками P_i, положение объекта на каждом сегменте которой определяется как безразмерным нормированным параметром t∈[0; 1] (фиг. 1), так и в последующем в реальном текущем масштабе времени. На фиг. 1 приведена траектория, состоящая из двух сегментов в виде кривых Безье 3-й и 1-й степеней, формируемых в соответствии с (1) соответственно векторами координат точек Р₀(0; 0), Р₁(3; 5.25); Р₂(6; 3), Р₃(10; 0) и С₀(10; 0) и С₁(12; -1.5). Точки P₃(10; 0) и С₀(10; 0) сопрягаемых сегментов кубической параболы и отрезка прямой имеют одинаковые координаты на плоскости. Для обеспечения плавного перехода с одной кривой Безье на другую обеспечено плавное изменение радиуса кривизны, что выполнимо при непрерывности первой и второй производных сопрягаемых кривых. Для обеспечения непрерывности первой производной в соответствии с (1) достаточно, чтобы три смежные опорные точки двух кривых (P₂, Р₃, С₀, С₁) лежали на одной прямой, тогда при построении траектории две сопрягаемые кривые будут иметь общую касательную в точке стыка С₀(10; 0), т.е. равные первые производные. Для обеспечения непрерывности второй производной необходимо, чтобы пять смежных вершин двух кривых лежали на одной прямой или составляли выпуклый многоугольник. Это означает, что вершины должны либо составлять выпуклый многоугольник, либо лежать на одной прямой, чтобы сохранить непрерывность на стыке. В данном случае достаточно 4-х точек Р₁, Р₂, Р₃, С₀, С₁, поскольку точки Р₃, С₀ общие для двух сегментов Данное требование существенно ограничивает множество кривых; поэтому на практике для соблюдения непрерывности вторых производных при сопряжении можно использовать полиномиальные кривые и более высокого порядка или несколько кубических кривых. Для упрощения изложения исследуем способы воспроизведения траекторий на плоскости сегментов кривых 1-3-й степеней с иллюстрацией на конкретных примерах.

Сопряжение кубической кривой с отрезком прямой.

Для построения произвольных траекторий движения объектов часто необходимо обеспечить выполнение сопряжения отрезка прямой и кривой Безье, а также сопряжение кривых Безье произвольных форм с исключением скачков скорости и допустимыми значениями суммарного ускорения, определяемого как векторная сумма центростремительного а_ц и тангенциального а_т ускорений. Например, широко распространенный переход объекта с прямолинейной на криволинейную траекторию и обратно не должен сопровождаться скачком центростремительной силы:

F_ц=mV²/R_k=ma=mgn_ц,

где R_k - радиус кривизны; V - линейная скорость по кривой; gn_ц - перегрузка (g=9.8 м/с² - ускорение свободного падения, n_ц - числовой коэффициент). Если известны допустимая перегрузка и линейная скорость объекта при его движении по криволинейной траектории, то можно рассчитать минимальный радиус кривизны дуги: R_kmin=V²/(gn_цmax). Так, при скорости самолета V=1000 м/с и максимальной переносимой пилотом перегрузке gn_цmax=8g минимальный радиус кривизны составит: R_kmin=12.74 км. Т.е. на предельных для самолета скоростях радиус кривизны на переходной кривой не может быть меньше 13 км.

Если радиус кривизны будет иметь меньшее значение, то необходимо менять опорные точки сопрягаемых сегментов траектории в (1) таким образом, чтобы обеспечить более плавный переход, или вводить кривые 4-й степени, или вместо одной кривой Безье использовать несколько кривых. Таким образом, при задании геометрической формы кривой необходимо одновременно определять и минимальный радиус ее кривизны. Следует также предусмотреть и запас на величину допустимого линейного ускорения, которое векторно суммируется с тангенциальным. Для данного случая сопряжения достаточно, чтобы три точки кубической кривой Безье (фиг. 1) Р₁(3; 5.25); Р₂(6; 3), Р₃(10; 0) находились на одной прямой с точками С₀ и С₁, задающими уравнение отрезка прямой. В соответствии с (1) при t∈[0; 1] уравнение кривой Безье третьего порядка будет иметь вид:

Для опорных точек Р₀(0; 0), Р₁(3; 5.25); Р₂(6; 3), Р₃(10; 0) (фиг. 1) в соответствии с (2) определим параметрические уравнения траектории, первую и вторую производные при сопряжении отрезка прямой и кривой Безье:

x(t)=9t+t³,

y(t)=15.75t-22.5t²+6.75t³.

Первая и вторая производная равны:

x''(t)=(9+3t²)'=6t,

y''(t)=(15.75-45t+20.25t²)'=40.5t-45.

Вторая производная по х определяет радиус кривизны

Таким образом, в конечной точке кубической кривой Безье P₃(10; 0) имеем нулевой радиус кривизны R=∞. В соответствии с параметрическим уравнением линейной кривой Безье B(t)=(1-t)P₀+t⋅P₁, сопрягаемого отрезка прямой с координатами С₀(10; 0) и С₁(12; -1.5), лежащей на одной прямой с точками Р₁-Р₃, получим параметрические уравнения по каждой из координат:

x(t)=10+2t,

y(t)=-1.5t

Уравнение прямой y=f(x) в прямоугольной системе координат будет иметь вид y=7,5-0,75x, т.е. действительно имеем совпадение первых производных сопрягаемой кубической кривой и отрезка прямой. И визуально из фиг. 1 следует, что имеем плавный переход от отрезка прямой с радиусом кривизны R=∞ до некоторого фиксированного минимального радиуса кривой Безье. Для определения максимальной перегрузки необходимо для кубической кривой определить минимальный радиус в соответствии с выражением:

и построить график зависимости (фиг. 2) R(t), по которой можно определить минимальный радиус кривизны.

Имитация траектории движения должна производиться в реальном масштабе времени, начиная с некоторого начального значения времени воспроизведения траектории Т_нач=0. После чего текущее значение времени можно представить в виде линейно нарастающей непрерывной или решетчатой функции времени t_p=kТ_т с некоторым дискретом Т_т. В то же время в соответствии с (1) кривая Безье для любого сегмента является функцией безразмерного нормированного параметра t∈[0; 1], который будем трактовать как некоторую функцию нормированного времени t∈[0; 1]. Нормированное время связано с реальным сложной функциональной зависимостью. Достаточно отметить, что для отдельных фрагментов траектории с разной длиной пути S_мах при постоянной скорости движения нормированное время прохождения по сегменту остается постоянным. Таким образом, для различных сегментов траектории с разной длиной пути и, естественно, например, при постоянной линейной скорости движения на этих участках необходимо перенормировать безразмерный параметр t∈[0; 1] к реальному значению времени t_p прохождения каждого заданного сегмента исходя из необходимого условия, что каждому максимальному нормированному значению t=1 будет соответствовать реальное время прохождения сегмента t_мах=S_мах/V.

Чтобы получить полную эффективную кинематику движения объекта по траектории в функции реального времени при изменении скорости, необходимо исследовать наиболее рациональные методы получения функциональных зависимостей нормированного значения времени t от аргумента t_p действительного текущего значения времени и наоборот. Однозначно нормированное и реальное время связывает пройденный путь S. Путь S и (или) текущее реальное значение времени могут быть связующим параметром для определения текущих нормированных значений времени, подставляемых в параметрические уравнения для воспроизведения текущих значений координат траектории

x(t)=9t+t³,

y(t)=15.75t-22.5t²+6.75t³.

В соответствии с вышеизложенным, предварительно определим функциональные зависимости: S(t), длины дуг - S_мах, пройденных по заданным сегментам, обратные функции t(S), а также их аппроксимации полиномами наилучшего приближения.

Определение пути пройденного по заданной кривой.

Путь, пройденный по параметрически заданной кривой на плоскости (фиг. 1) в функции нормированного времени, определяется формулой:

Например, путь вдоль линейной кривой Безье из т. Р₃(10; 0) в т. С₁(12; -1.5) в соответствии с параметрическими уравнениями x(t)=10+2t, y(t)=-1.5t будет равен . Путь, пройденный по параметрически заданной кубической кривой на плоскости (фиг. 1), равен .

Поскольку для интеграла (3) табличное представление отсутствует, то его можно определить в системе MathCAD путем численного интегрирования. При этом можно получить как длину пути S_мах на заданном сегменте, так и точные, отдельные значения и графики функций S(t) и t(S) (фиг. 3-6). Монотонно изменяющиеся прямые и обратные функциональные зависимости S(t), t(S) можно и аппроксимировать с высокой степенью точности полиномами наилучшего приближения 2-й или 3-й степеней в соответствии с их графиками (фиг. 3-6). Для параметрических уравнений кривой Безье:

x(t)=9t+t³,

y(t)=15.75⋅t-22.5⋅t²+6.75⋅t³.

В соответствии с графиком функций S(t) получен полином наилучшего приближения 2-й степени g(t)=0.462+10.495⋅t+1.05⋅t². Коэффициенты полинома вычислены исходя из матричных уравнений

при оптимальных узлах аппроксимации полинома (значения безразмерного параметра t нормированного времени) 0.075, 0.5 и 0.895.

Аппроксимирующий полином 3-й степени: g(t)=0.077+16.298⋅t-13.258⋅t²+9.129⋅t³ получен в соответствии с матрицами

Аппроксимация обратной функциональной зависимости t(S) практически произведена с помощью полинома наилучшего приближения g(t)=0.436+10.614⋅t+0,916⋅t² в соответствии с матричными уравнениями

Для значительного уменьшения погрешности в соответствии с графиком функции t(S) получен полином наилучшего приближения 3-й степени g(t)=0.095+16.116⋅t-12.862⋅t²+8.896⋅t³. Коэффициенты полинома вычислены исходя из матриц

Построены графики погрешности аппроксимирующих полиномов 2-й и 3-й степеней для обратной функции.

Относительная приведенная погрешность аппроксимации текущего значения пути не превышает для полиномов второй и третьей степеней соответственно 0.365/12.223=0.0298 и 0.108/12.223=0.0088. Т.е. значение погрешности уменьшилось в 0.0298/0.0088=3.39 раз. Определенные параметры, уравнения аппроксимации функциональных зависимостей являются исходными для определения кинематических параметров движения объекта, текущих значений координат траектории в функции реального времени.

Расчет параметров кинематики при равномерном и равноускоренном движении объекта. Комплексирование отдельных сегментов в траекторию в функции реального времени.

Движение с постоянной скоростью является наиболее простым и в то же время наиболее распространенным способом движения. Для первого сегмента траектории с такими условиями можно принять начальное значение времени Т_нач=0. При воспроизведении сегмента траектории в виде отрезка прямой с равномерным движением зависимость пути как от нормированного, так и от реального времени будет линейной. И при подстановке в параметрические уравнения воспроизведения траектории текущих нормированных значений времени (безразмерных значений параметра) при равномерном движении по отрезку прямой необходимо использовать выражение t=t_p/t_мах, где реальное время прохождения сегмента t_max=S_мax/V. При равномерном движении по кубической кривой для текущих значений t_p на заданном сегменте определяются линейно-нарастающие значения пути S=V_tp. По текущим значениям S определяются в соответствии с аппроксимирующим обратную функцию t(S) полиномом (фиг. 6.) нормированные значения времени t. После чего по параметрическим уравнениям вычисляются текущие значения прямоугольных координат.

При переменной скорости движения по сегментам расчет временных параметров будет более сложным. При равнозамедленном, равноускоренном или других видах движения для исключения скачков скорости и ускорения линейная скорость и ускорение в начале следующего сегмента движения должны быть равны скорости и ускорению в конце предшествующего сегмента. Текущее значение пути при равноускоренном движении по заданному отрезку прямой или кривой можно определить в соответствии с формулой S=Vt_p+at_p²/2. После чего по аргументу - текущему пути S с помощью полинома, аппроксимирующего обратную функцию t(S) (фиг. 6.), как и ранее, определяется нормированное время t. Например, для отрезка прямой в функции нормированного времени t(S) определяются текущие значения координат

x(t)=10+2t,

y(t)=-1.5t.

При более сложных заданиях функции скорости от времени значение пути на сегменте вычисляется с помощью интеграла .

Комплексирование, стыковка отдельных сегментов траектории может быть произведена последовательно исходя из следующих положений. Форму сегмента, его длину - максимальное значение пути S_мax по сегменту - можно определять и варьировать при задании геометрической формы кривой. При назначенном значении начальной скорости величину ускорения, например, при равноускоренном движении можно изменять так, чтобы получить заданное время прохождения сегмента траектории в соответствии с квадратным уравнением .

Например, при S=1000 м, V_нач.=10 м/с, а=2 м/с² получим и т.д.

Итак, в соответствии с параметрическими уравнениями каждого сегмента в функции безразмерного параметра t вычисляется путь, пройденный по параметрически заданной кубической кривой в функции S(t), воспроизводится обратная функция t(S) с последующей аппроксимацией ее полиномом наилучшего приближения g(S), по заданному закону воспроизведения скорости на заданном сегменте определяются текущее значение пройденного пути S(t_p1) в функции текущего временного интервала t_p1 от начала сегмента и времени движения по сегменту, время прохождения сегмента, по общему, связывающему параметру текущего пути S на сегменте осуществляется переход от времени t_p1 к параметру t с последующей подстановкой его в параметрические уравнения вычисления прямоугольных координат.

После проведения предварительных расчетов имеем отдельные сегменты, для начала и концов которых заданы абсолютные начальные и конечные значения прямоугольных координат, привязанные к точке стояния РЛС. Произведена привязка начала и конца формирования каждого сегмента траектории к реальному значению текущего временного интервала, формируемого таймером реального времени. Для каждого сегмента получены: время воспроизведения его начала и время завершения, уравнения зависимости длины пути в сегменте от начала сегмента в функции относительного реального времени от начала временного интервала формирования сегмента, аппроксимирующие полиномы для воспроизведения зависимостей нормированного времени t(S) в каждом сегменте, параметрические уравнения воспроизведения координат в функции нормированного времени в каждом сегменте. Предварительные действия оператора, направленные на проектирование модели движения, подготовительные расчеты обеспечивают в общем временном интервале формирования траектории движения определение моментов времени начала, продолжительности и окончания движения объекта по каждому сегменту, которые позволяют идентифицировать именно тот сегмент, по которому перемещается объект в момент времени t_p воспроизведения каждого сегмента, с присвоением ему порядкового номера. К каждому порядковому номеру сегмента привязывается таблица уравнений движения на заданном сегменте.

Все рассчитанные функциональные зависимости, уравнения движения заносятся в память, например, рабочего места инструктора-оператора. После чего они, как и в прототипе, в момент начала тренировки с воспроизведением траекторий движения на экране системы отображения информации рабочего места оператора передаются в блок расчета координат в соответствии с заданными геометрическими и кинематическими параметрами траектории. С начала тренировки, как и в прототипе, по линейно-нарастающему временному интервалу с таймера блок вычисления координат определяет время начала работы на очередном сегменте, вычисляет текущие прямоугольные координаты в пределах сегмента, фиксирует время перехода к следующему сегменту.

Литература

1. Каханер Д., Моулер К., Нэш С. Численные методы и программное обеспечение: пер. с англ. - М.: Мир, 2001. - 575 с.

2. Патент №2419072. Способ имитации траекторий движения воздушных объектов. / Опубл. 20.05.2011. - Бюл. №14 (Чекушкин В.В., Аверьянов A.M., Бобров М.С.).

3. Чекушкин В.В., Аверьянов A.M., Бобров М.С. Имитация траектории движения объектов для радиолокационных систем управления и контроля воздушного пространства // Мехатроника, автоматизация, управление. №9, 2009. С. 70-78.

4. Патент РФ на изобретение №2489753 от 10.08.2013. «Способ и устройство имитации радиолокационной информации» // Изобретения. Полезные модели. 2013, Бюл. №22 (Антуфьев Р.В., Бобров М.С., Пискунов Г.Г., Чекушкин В.В., Пантелеев И.В., Царьков М.А.).

5. Свидетельство о гос. регистрации программы для ЭВМ №2009611848 от 09.04.2009 «Программа сглаживания траекторий движения воздушных объектов для радиолокационных систем управления (Trajectory)». Заявка №2009610537 от 16.02.2009.

1. Способ имитации траекторий движения воздушных объектов путем ручного ввода координат опорных точек траектории с указанием скоростей движения в этих точках и автоматического расчета уравнений движения по трем координатам x(t_p), y(t_p), z(t_p) и скорости V(t) непосредственно после ввода исходных данных на рабочем месте оператора с последующей передачей коэффициентов указанных уравнений в блок расчета координат, в котором в ответ на запрос информации о текущем положении объекта вычисляются его декартовы координаты путем подстановки реального времени t_p в уравнения движения, соответствующие преодолеваемому в момент t_р участку траектории, для чего траектория движения воздушного объекта представляется состоящей из элементарных сегментов в виде отрезков прямых, сопряжение которых при значении угла между ними ϕ<90° производится с исключением скачков скорости и ускорения согласующими участками в виде дуги окружности и двух сегментов кубических парабол, на которых радиус кривизны R_к плавно меняется от бесконечного в точках стыка с прямолинейными участками до радиуса согласования R_с в точках стыка с участком в виде дуги окружности или с исключением участка в виде дуги окружности при значении угла между согласуемыми отрезками прямых ϕ≥90°, отличающийся тем, что положение и геометрическое представление траектории движения объекта в пространстве плавно комплексируется из последовательно сопрягаемых сегментов с итерационными, наглядными графическими интуитивными изменениями их формы и кривизны, расчетом параметрических уравнений движения в каждом сегменте по трем координатам x(t), y(t), z(t) зоны обзора радиолокационной станции в функции безразмерного параметра t∈[0; 1] с преобразованием его при различных законах изменений линейной скорости движения в функцию от аргумента - линейно-нарастающего временного интервала реального времени t_p воспроизведения траектории путем определения проходимого по сегментам пути S(t_p), вычисления в соответствии с обратной функцией значений t(S) в каждом сегменте и последующим вычислением в блоке расчета координат по параметрическим уравнениям движения значений текущих декартовых координат объекта.

2. Способ по п. 1, отличающийся тем, что геометрическая форма каждого сегмента общей траектории движения гибко, интуитивно выстраивается на основе итерационного изменения расположения координат n опорных точек ({P_i}={x_i, y_i, z_i}, i=0, …, n-1) опорной ломаной линии кривой Безье сегмента с n узлами, автоматическим расчетом параметрических уравнений движения в каждом сегменте по трем координатам x(t), y(t), z(t) зоны обзора радиолокационной станции в функции безразмерного параметра t∈[0; 1], по параметрическим уравнениям определяется максимальный путь по сегменту S_мах - длина сегмента, минимальный радиус кривизны, обеспечивающий проверку и исключение критических перегрузок при максимальных линейных скоростях движения.

3. Способ по п. 2, отличающийся тем, что переход с одного сегмента кривой Безье на другой производится с плавным изменением радиуса кривизны, обеспечением непрерывности первой и второй производных двух сопрягаемых кривых, когда для сопрягаемых сегментов из кубической параболы и отрезка прямой или двух кубических парабол соответственно их пять смежных вершин лежат на одной прямой или составляют выпуклый многоугольник.

4. Способ по п. 1, отличающийся тем, что в соответствии с параметрическими уравнениями каждого сегмента в функции безразмерного параметра t вычисляется путь, пройденный по параметрически заданной кубической кривой в функции S(t), воспроизводится обратная функция t(S) с последующей аппроксимацией ее полиномом наилучшего приближения g(S);

по заданному закону воспроизведения скорости на заданном сегменте определяются текущее значение пройденного пути S(t_p1) в функции текущего временного интервала t_p1 от начала сегмента и времени движения по сегменту, время прохождения сегмента,

по общему, связывающему параметру текущего пути S на сегменте осуществляется переход от времени t_p1 к параметру t с последующей подстановкой его в параметрические уравнения вычисления прямоугольных координат.

5. Способ по п. 1, отличающийся тем, что предварительные действия оператора, направленные на проектирование модели движения, подготовительные расчеты обеспечивают в общем временном интервале формирования траектории движения определение моментов времени начала, продолжительности и окончания движения объекта по каждому сегменту, которые позволяют идентифицировать именно тот сегмент, по которому перемещается объект в момент времени t_p воспроизведения каждого сегмента, с присвоением ему порядкового номера, к каждому порядковому номеру сегмента привязывается таблица уравнений движения на заданном сегменте.

6. Способ по п. 1, отличающийся тем, что при формообразовании обрабатываемых деталей геометрическая форма траектории движения рабочего органа привязывается к системе координат робототехнического комплекса или станка с числовым программным управлением, а скоростной режим движения определяется их динамическими характеристиками.