Способ определения составляющих ударной вязкости металла при испытании на ударный изгиб

Способ определения составляющих ударной вязкости металла при испытании на ударный изгиб

Иллюстрации

Показать все

Реферат

Изобретение относится к определению механических свойств металла, а именно к способам разделения ударной вязкости на работу зарождения и работу распространения трещины при испытании на ударный изгиб, и может быть использовано в металлургии, машиностроении и других отраслях народного хозяйства.

Для испытания металла на ударную вязкость используются стандартные образцы в соответствии ГОСТ 9454-78 Металлы. Метод испытания на ударный изгиб при пониженных, комнатной и повышенных температурах. Испытания проводят на маятниковом копре, например МК-30 (запас работы удара составляет 300 Дж). Ударная вязкость определяется работой разрушения образца при испытании на ударный изгиб.

Процесс разрушения металла, в частности, при испытании на ударный изгиб состоит из зарождения и распространения трещины. Работа (А), затраченная на разрушение образца металла, складывается из работы зарождения трещины (А_з) и работы ее распространения (А_р) по образцу.

Величины работы зарождения и работы распространения трещины являются важными характеристиками, определяющими служебные свойства металла и влияющими на долговечность конструкции. Поэтому разделение работы удара при испытании на ударную вязкость является важной и актуальной проблемой металловедения.

Существует ряд способов разделения работы удара на работу зарождения и работу распространения трещины.

По способу Отани [1] используется стандартный образец при испытании на ударную вязкость. Испытание проводится на маятниковом копре. В результате заранее проведенных испытаний на образцах подбирают такую работу маятника, при которой только образуется трещина. Эта работа принимается за работу зарождения трещины. Затем образец с трещиной помещают в специальный красящий раствор, например CuSO₄, для осаждения на поверхностях трещины красящего осадка. Второй (окончательный) удар определяет работу распространения трещины. На образцах, разрушенных при испытании, видна окрашенная поверхность разрушения. Выбирают тот образец, где длина предварительно нанесенной трещины наименьшая. Работу первого удара на этом образце принимают за работу зарождения трещины, а работу второго удара - за работу распространения трещины. Недостатками метода Отани являются наличие предварительного удара и соответственно с этим подбор соответствующей работы, необходимой только для образования трещины, наличие окрашивающего раствора, субъективное определение длины окрашенной области. Для получения результата необходимо использовать несколько образцов.

Указанные недостатки способа Отани снижают точность определения работ зарождения и развития трещины. Кроме того, для этого способа температура испытания должна быть не ниже минус 30°C [2].

Известен способ разложения ударной вязкости на работу зарождения и развития трещины по Лифшицу-Рахманову [3-5]. Образцы исследуемого материала при одинаковом сечении под надрезом нагружают до разрушения изгибающим ударом, определяют для каждого образца поглощенную энергию и работу зарождения трещины. Находят зависимость поглощенной энергии от работы зарождения трещины, а работу развития трещины определяют экстраполяцией данной зависимости на значение, соответствующее нулю работы зарождения трещины.

По способу Б.А. Дроздовского [6] испытывают образцы с V-образным надрезом с заранее образованной с помощью вибратора усталостной трещиной. Считается, что при разрушении образца вся работа динамического удара расходуется на распространение трещины. При таком испытании определяется работа распространения трещины. Работа зарождения трещины подсчитывается как разность между работой разрушения при изгибе на образце без усталостной трещины и работой ее распространения.

Недостатками способа Дроздовского являются:

- образование трещины осуществляется путем циклического нагружения, которое может изменить исходные свойства материала;

- субъективный выбор длины трещины, которая принимается за зародышевую.

Наиболее близким к заявляемому техническому решению по технической сущности и достигаемому техническому результату является способ разделения ударной вязкости на работу зарождения и распространения трещины по Гуляеву А.П. [7].

Суть способа состоит в следующем. Подготавливают две группы стандартных образцов одинакового поперечного сечения и длины на ударную вязкость.

Первая группа образцов с U-образным концентратором напряжений радиуса R=1 мм (тип 1, ГОСТ 9454-78) и вторую группу образцов с V-образным концентратором напряжений с радиусом R=0,25 мм (тип 11, ГОСТ 9454-78). Образцы первой и второй групп испытывают на ударный изгиб при одинаковой температуре и определяют работу разрушения при U-образном и V-образном концентраторах напряжений. Затем графическим построением определяют зависимость работы удара от радиуса концентратора напряжений. На фиг. 2 представлена схема указанной зависимости. Экстраполируя полученную зависимость при R=0, получим значение работы удара, которая принимается за работу распространения трещины (А_р). Затем, вычитая из работы разрушения образца (А) значение работы распространения трещины при U-образном (надрезе) концентраторе напряжений ,находим работу зарождения трещины (А_з):

Основными недостатками прототипа являются следующие:

- принимается, что работа образования трещины не зависит от вида концентратора напряжения. Это допущение является приближенным, так как не учитывает различие схем напряженно-деформированного состояния в месте концентратора напряжений (надрезе). При U-образном и V-образном надрезах схемы напряженно-деформированного состояния различные [2];

- графическая экстраполяция определения работы распространения трещины имеет субъективную и объективную погрешность. Наличие субъективной составляющей погрешности при графической экстраполяции искажает получаемый результат;

- работа образования трещины определяется не независимо, а из полученных ранее данных: работы удара и работы распространения трещины в соответствии с формулой (1).

Технической задачей изобретения является расширение технологических возможностей способа разделения работы удара на работу зарождения и распространения трещины.

Поставленная задача решена следующим образом.

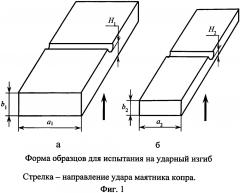
Из нужного материала изготавливают образцы для испытания на ударный изгиб с одинаковыми концентраторами напряжения, но с разными площадями поперечного сечения в месте концентратора напряжений. Размеры площади сечения соответствуют стандартным размерам (по ГОСТ 9454-78).

Площадь поперечного сечения первого образца (фиг. 1а) в месте концентратора напряжений (надреза) составляет S₁=a₁⋅H₁. Для второго образца - S₂=а2⋅H₂ (фиг. 1б), где a и H - соответственно ширина и высота образца в месте надреза. При испытании на ударный изгиб работа разрушения первого образца составляет A₁, а для второго образца составляет A₂. Работу разрушения образца представляем как сумму работ зарождения (А_з) и распространения трещины (А_р):

Тогда для первого образца можно записать:

Для второго образца партии:

Работа зарождения трещины зависит от качества материала и длины стороны, по которой производится удар ножа маятникого копра (фиг. 1, размер «a»), может быть представлена как:

где α - удельная энергия образования трещины [Дж/м].

Тогда работа зарождения трещины будет равна:

- для первого образца:

- для второго образца:

Работа распространения трещины зависит от качества материала и от площади, проходимой трещиной через образец (фиг. 1, размеры «a» и «H»), может быть представлена так:

где β - удельная энергия распространения трещины [Дж/м²].

Тогда работа распространения трещины будет равна:

- для первого образца:

- для второго образца:

С учетом формул (5) и (8) работа, затраченная при разрушении i-го образца, будет равна:

Соответственно для первого и второго образцов имеем:

Решая совместно систему из уравнений (12) и (13):

получаем значения α и β.

Работы зарождения и распространения трещин для первого и второго образцов вычисляем соответственно по формулам (6, 7) и (9, 10).

Пример конкретного выполнения.

Из листовой стали марки A32 толщиной 10 мм изготовляли образцы для испытания на ударный изгиб. Размеры сечения образцов в месте надреза составляли (ширина × высота): 6×6 мм; 8×9 мм. Все образцы имели U-образный концентратор напряжения (надрез). Образцы испытывали на ударный изгиб на маятниковом копре МК-30 с определением работы разрушения образца при температуре минус 40°C. По результатам испытаний составляли систему алгебраических уравнений с учетом уравнения (11)

Решая эту систему уравнений, определяем значения удельной энергии образования трещины (α) и удельной энергии распространения трещины (β). Исходные данные и вычисленные значения работ зарождения и распространения трещины приведены в таблице. Относительная погрешность определения работ зарождения и распространения трещины не превышает 3,5%.

Для сравнения было проведено определение работ образования и распространения трещины по прототипу (способ Гуляева А.П.). Были изготовлены из того же материала, что и по предлагаемому способу, две партии образцов стандартного размера с U-образным концентратором напряжения, где радиус надреза R=1,0 мм, и V-образным надрезом, где радиус надреза R=0,25 мм. Испытания на ударный изгиб проводили на том же копре М-30 при температуре минус 40°C. По полученным значениям работы удара строили зависимость работы удара от радиуса надреза (фиг. 3). При экстраполяции при R=0 получено, что работа удара в этом случае будет 120 МДж. Это значение в соответствии со способом Гуляева А.П., принято за работу распространения трещины. Работа образования трещины вычисляется как разность работы удара образца с U-образным концентратором напряжения (170 МДж) и работы распространения трещины (120 МДж). Таким образом, работа зарождения трещины равна 50 МДж. Различие результатов по прототипу и предлагаемому способу составляет не более 10%.

Преимуществами предлагаемого способа являются:

- отсутствие субъективных оценок технологического процесса испытания образцов. Все параметры а, H, A измеряются объективно: размеры сечения - измерительным инструментом с определенной погрешностью; работа удара - по измерительному механизму маятникового копра;

- значения работ образования и распространения трещины являются независимыми между собой величинами и определяются только по работе удара из системы уравнений (14);

- применение аналитического метода расчета работ образования и распространения трещины вместо графического метода, как по прототипу, повышает точность измерения этих величин;

- для испытаний применяются образцы с одинаковыми концентраторами напряжений (U-образный или V-образный), поэтому образование трещины происходит при одной схеме напряженно-деформированного состояния;

- при испытании используются образцы с разными размерами площади поперечного сечения, что позволяет оценить значения работ образования и распространения трещины на листовом прокате разной толщины. Это расширяет технологические возможности способа.

Список использованной литературы

1. Отани М. Исследование чувствительности сварных соединений к надрезу при динамических испытаниях двойным ударом / М. Отани // Тэцудо гидзюцу кэпкю сирё. - 1957. - Т. 14, №11 - С. 503-529.

2. Пашков Ю.И. К вопросу оценки трещиностойкости труб по ударной вязкости и пробе ДWTT / Ю.И. Пашков, М.А. Иванов // Вестник ЮУрГУ. Серия «Металлургия». - 2014. - Т. 14, №4 - С. 52-58.

3. Лифшиц Л.С. Об определении ударной вязкости при низких температурах и склонности металла к зарождению и развитию трещин / Л.С. Лифшиц, А.С. Рахманов // Заводская лаборатория. - 1953. - №2 - С. 51-54.

4. А.С. СССР. Лифшиц Л.С., Рахманов А.С. Об определении ударной вязкости материала. №1559267. Опуб. 23.04.90. Бюл. №15.

5. Бакши О.А. Метод определения составляющих ударной вязкости / О.А Бакши, А.Н Моносиков, А.Г Кукин // Заводская лаборатория. 1969. - №5 - С. 615-619.

6. Дроздовский Б.А. О применении статического изгиба образцов с надрезом для количественной оценки кристалличности в изломе стали / Б.А. Дроздовский // Заводская лаборатория. - 1946. - №4 - С. 489-499.

7. Горицкий В.М. Диагностика металлов. Металлургиздат. 2004. 408 с.

Способ определения составляющих ударной вязкости материала при испытании на ударный изгиб, включающий определение работы разрушения образца (А) при постоянной температуре, отличающийся тем, что испытывают два образца с одинаковыми концентраторами напряжения и различными размерами поперечного сечения в месте надреза, а работу зарождения и работу распространения трещины соответственно для первого (А_З1 и A_p1) и для второго (А_З2 и А_p2) образцов рассчитывают по формулам

А_З1=а₁⋅α; А_З2=а₂⋅α;

A_Pl=a₁⋅H₁⋅β; А_Р2=а₂⋅Н₂⋅β,

где α - удельная работа зарождения трещины в образцах данного материала;

β - удельная работа распространения трещины для данного материала рассчитываются из системы уравнений

где А₁ и А₂ - работа удара для первого и второго образцов,

a ₁, Н₁ и a₂, H₂ - размеры сечения первого и второго образцов в месте надреза.