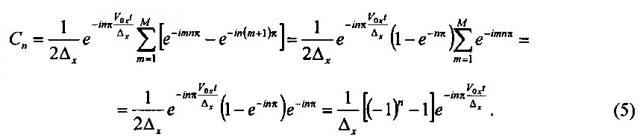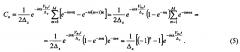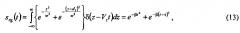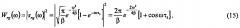Способ измерения поля скоростей в газовых и конденсированных средах

Способ измерения поля скоростей в газовых и конденсированных средах

Иллюстрации

Показать все

Реферат

Изобретение относится к измерительной технике и может найти применение в экспериментальной гидро- и аэродинамике, в промышленных технологиях, связанных с необходимостью исследования полей скоростей в потоках газовых и конденсированных сред, а также скоростей движения поверхностей.

Известны способы, предназначенные для измерения поля скоростей в газовых и конденсированных средах методами когерентной и некогерентной оптики. К ним относятся лазерные доплеровские измерения поля скоростей (в англоязычной литературе - Doppler Global Velocimetry - DGV) [Dubnishchev Yu., Chugui Yu. V., Kompenhanc Jurgen, Belousov P.P., Belousov P.Ya. Method and Device for Laser Doppler Measurement of a Velocity Field of a Fluid Flow. EP 1978369 B1, G01P 3/36. Publication 03.03.2010 Bulletin 2010/09], измерения по трекам изображений частиц (Particle Image Velocimetry - PIV) [Raffel M., Willert CE., Kompenhans J. (1998). Particle Image Velocimetry. Springer, Berlin]. Измерение поля скоростей методом DGV заключается в последовательном выполнении следующих операций: освещают сечение исследуемой среды лазерной плоскостью, конвертируют доплеровский сдвиг частоты рассеянного света в интенсивность и регистрируют изображения лазерной плоскости в конвертированном свете. Распределение интенсивности конвертированного света в изображении лазерной плоскости на фотоматрице отображает поле скоростей в исследуемом сечении.

Недостатком способа DGV является зависимость числа каналов регистрации частотно-конвертированных изображений лазерной плоскости от размерности координатно-измерительного базиса (числа проекций) вектора скорости. К другим недостаткам следует отнести требование тонкой температурной стабилизации конвертора частота-интенсивность, обычно выполняемого на основе молекулярной ячейки поглощения или интерферометра, необходимость автоматической привязки когерентно-оптической передаточной функции конвертора к частоте излучения лазера и использование только когерентного излучения. В методах PIV недостатком являются ограничения на пространственно-временное разрешение исследуемых процессов из-за проблем с идентификацией треков при высокой концентрации частиц и многократной экспозиции.

Кроме того, известен способ [Shigeo Hasokawa, Akio Tomiyama. Spatial Filter Velocimetry Based on Time-Series Particles Images. Exp. Fluid (2012). 52: p.1361-1372], являющийся прототипом предложенного изобретения, основанный на эмуляции динамической пространственной фильтрации изображений движущихся частиц, регистрируемых на фотоматрице при видеосъемке. Частицы движутся в выделенном световой плоскостью сечении исследуемой среды. При считывании изображений частицы в процессе воспроизведения фильма на программном уровне в пиксельной структуре формируется периодическая дискретизирующая последовательность с заданным пространственным периодом и фазовой скоростью, которая эмулирует динамический пространственный фильтр. Этот фильтр трансформирует скорость пространственного перемещения изображения частицы вдоль координатной оси, заданной дискретизирующей последовательностью, в частоту. Измеряя эту частоту и учитывая коэффициент линейного увеличения оптической системы, формирующей изображение, получают величину скорости движения частицы в заданной световой плоскости.

Недостатком этого способа является невозможность получения информации о пространственном поле 3D векторов скоростей в исследуемых газовых и конденсированных средах.

Задачей (техническим результатом) предлагаемого изобретения является расширение функциональных возможностей на измерение 3D поля скоростей в газовых и конденсированных средах.

Решение поставленной задачи достигается тем, что в известном способе структурированное зондирующее поле в исследуемой среде формируют в виде параллельных световых плоскостей на длинах волн, соответствующих цветовой чувствительности пикселей фотоматрицы, движущихся в этих плоскостях. Изображения световых плоскостей одновременно формируют на фотоматрице в телецентрической проекции, эмуляцию динамической пространственной фильтрации выполняют на пиксельных структурах, световая чувствительность которых согласована с длиной волны соответствующей световой плоскости. Получают корреляционные функции попарных изображений световых плоскостей, а поле нормальных к световым плоскостям компонент скорости определяют как пространственное распределение отношения попарного расстояния между световыми плоскостями к интервалам между экстремумами в соответствующих корреляционных функциях. Этим обеспечивается получение информации о пространственном поле скоростей частиц в исследуемой среде.

На Фиг. 1 показана структурная схема устройства, реализующего предложенный способ.

На Фиг. 2 показаны спектры эмулированных фильтрованных сигналов на пикселах.

На Фиг. 3 показаны r, g и b - сечения световых плоскостей.

На Фиг. 4 показана корреляционная функция K_srg (τ) фильтрованного сигнала.

Устройство (Фиг. 1) содержит: конфокальные объективы 1 и 2 с пространственным фильтром 3, расположенным в совмещенной фокальной плоскости, которые образуют телецентрическую систему, проектирующую на фотоматрицу видеокамеры 4 изображение структурированного зондирующего поля, сформированного в исследуемой среде. Видеокамера подключена к компьютеру 5. Телецентрическая система [Бычков P.M., Чугуй Ю.В. Беседы о геометрической оптике. Изд-во Сибирского отделения российской академии наук, 2011, 476 с.] обеспечивает формирование изображения структурированного светового поля на фотоматрице с одинаковым коэффициентом увеличения в широких пределах, независимо от положения на оптической оси. Зондирующее поле состоит из параллельных световых плоскостей. Длины волн λ_r, λ_g и λ_b соответствуют световым чувствительностям пикселей в структуре фотоматрицы. В rgb-кодировке это красный, зеленый и синий цвета.

Способ осуществляется следующим образом. Оптические неоднородности, присутствующие в среде, отслеживают ее движение и, попадая в световые плоскости, рассеивают свет. Изображения оптических неоднородностей в рассеянном свете, сформированные в телецентрической проекции с известным коэффициентом передачи, фиксируются пиксельной структурой соответствующей цветовой чувствительности на фотоматрице и записываются в последовательности кадров цветного видеофильма. Реструктуризация полей скоростей движения оптических неоднородностей в световых плоскостях выполняется путем динамической пространственной фильтрации на длинах волн λ_r, λ_g и λ_b при компьютерном воспроизведении фильма. Периодическая структура динамического пространственного фильтра эмулируется в процессе считывания пиксельной структуры изображений частиц с известным межкадровым интервалом воспроизводимого фильма. Считывание выполняется по строкам и столбцам пиксельной структуры кадра, которым можно сопоставить ортогональные оси x и у в декартовой системе.

Рассмотрим динамическую пространственную фильтрацию изображения частицы, сформированного в световом поле с длиной волны λ_r. Изображение частицы или оптической неоднородности рассматривается как пространственный сигнал, фиксируемый пиксельной структурой фотоматрицы. Дискретизирующая последовательность, эмулирующая одномерный динамический пространственный фильтр при считывании одной строки по оси x, может быть описана выражением:

где Δ_х - пространственный полупериод дискретизирующей последовательности, состоящий из заданного числа пикселей; V_0x=Δ_х/τ₀; τ₀ - межкадровый интервал;

V_0x - фазовая скорость по оси х эмулированного пространственного фильтра с периодом 2Δ_х; δ(х-V_0xt-mΔ_х) - дельта функция Дирака;

t - время;

m - порядковый номер пространственного полупериода. Суммирование идет по числу полупериодов в дискретизирующей последовательности, которая эмулирует динамический пространственный фильтр.

Пусть одномерное сечение пространственного сигнала, изображение которого сформировано в свете с длиной волны λ_r (красный цвет), описывается функцией s(x-V_xt), где V_x - скорость движения изображения по оси х. Тогда для дискретизированного пространственного сигнала имеем:

Разложим дискретизирующую последовательность η_r(x) в РВД Фурье:

где

Учитывая фильтрующие свойства δ -функции, получаем из (4)

Здесь учтено: e^inπ=(-1)ⁿ; e^i2nπ=1. Подставляя (5) в (3) получаем

Выражение для дискретизированного сигнала находится подстановкой (6) в (2):

Пренебрегая в (7) высшими гармониками (|n|>1), получаем с точностью до знака:

Здесь - пространственная частота дискретизирующей последовательности. В (8) К_0х является волновым числом эмулированного гармонического пространственного фильтра cos[K_0x(x-V_0xt)], фазовая скорость которого V_0x;

V_x проекция скорости движения изображения частицы по оси x.

Переходя в (8) к лабораторной системе отсчета, получаем:

где ω_x=K_0xV_x; ω_0х=K_0xV_0x.

Отсюда

Эмуляция пространственного фильтра по оси у (по столбцам матрицы) осуществляется по аналогии с описанной выше процедурой. Выполняя считывание столбца по оси у, получаем для дискретизированного сигнала с точностью до знака:

где ω_y=K_0yV_y;

ω_0у=K_0yV_0y;

Отсюда для у-проекции скорости движения изображения частицы находим:

Частоты ω_0х и ω_0у возникают при динамической фильтрации изображений неподвижных частиц и неоднородностей фона. Выражения (9) и (11) описывают эмуляцию динамической пространственной фильтрации изображения в плоскости х, у. Частоты ω_х, ω_0х, ω_у и ω_0у определяются, например, посредством преобразования Фурье эмулированных сигналов. Переход от частот ω_х, ω_0х, ω_у и ω_0у к скоростям V_x и V_y на выбранных пространственных масштабах выполняется по формулам (10) и (12).

Пространственная реконструкция поля векторов скоростей реализуется при формировании структурированного зондирующего поля в виде параллельных световых плоскостей на длинах волн, соответствующих цветовой чувствительности пикселей в структуре фотоматрицы (например, λ_r, λ_g и λ_b). Действительные величины компонент скорости движения частицы определяются как V_x/Г и V_y/T, где Г - коэффициент увеличения оптической системы, формирующей изображения. Совершенно аналогично выполняется измерение поля х- и у-компонент вектора скорости движения частиц в других световых плоскостях, цвет которых, например, зеленый (g) и синий (b), согласован с цветовой чувствительностью пикселей фотоматрицы.

Измерение векторов скоростей V_x и V_y в параллельных лазерных плоскостях, сформированных излучением с длинами волн λ_r, λ_g и λ_b, осуществляется эмулированием пространственной фильтрации. Пример хроматической селекции сигналов, полученных в эксперименте, показан на Фиг. 2, где компонента спектра на частоте 10,4 Гц соответствует движущейся частице, а компонента спектра на частоте 6,3 Гц - неподвижному фону. Эмуляция пространственной фильтрации движения частицы по оси х получена на спеклах с цифровой чувствительностью λ_r (Фиг. 2, а), λ_g (Фиг. 2, b) и λ_b (Фиг. 2, с).

Формирование зондирующих параллельных r, g и b лазерных плоскостей на заданных расстояниях друг от друга в сочетании с хроматической селекцией изображений на фотоматрице позволяет измерять 3D поле скоростей. Измерение z-компоненты векторов скоростей, ориентированной по нормали к световым плоскостям, выполняется путем корреляционной обработки хроматически селектированных сигналов.

Обратимся к Фиг. 3. На этом чертеже показаны сечения r, g и b - световых плоскостей в исследуемой среде. Ось z является нормалью к световым плоскостям. Поскольку для формирования световых плоскостей, зондирующих исследуемую среду, обычно используются лазерные пучки, сечения световых плоскостей описываются гауссовыми функциями:,и, где w_r, w_g и w_b - радиусы перетяжек лазерных пучков по оси z [Ю.Н. Дубнищев. Теория и преобразование сигналов в оптических системах. С.Петербург, Изд-во «Лань», 2011, 368 с.]. Выберем эти перетяжки одинаковыми: w_r=w_g=w_b. Пусть в направлении z движется рассеивающая частица, которую, не нарушая общности рассуждений, будем считать точечной, моделируемой дельта-функцией δ(z-V_zt). Расстояния между r и g световыми плоскостями, как это показано на Фиг. 1 и Фиг. 3, равно d₁, а расстояния между g и b световыми плоскостями равно d₂. Световые поля, рассеянные частицей при пересечении пространственного интервала d₁ между плоскостями, сформированными на длинах волн λ_r, и λ_g, описываются выражением:

где

При интегрировании в (13) мы воспользовались фильтрующим свойством δ-функции. Найдем фурье-спектр сигнала (13):

Переходя от фурье-спектра к энергетическому спектру сигнала, получаем:

Корреляционную функцию сигнала s_rg(t) находим, выполняя фурье-преобразование энергетического спектра W_rg(ω):

Структура полученной корреляционной функции показана на Фиг. 4. Корреляционная функция (16) имеет максимумы в точках τ=0, τ=τ₁ и τ=-τ₁. Поскольку , скорость движения частицы на пространственном интервале d₁ определяется как

Описанный выше способ определения z-компоненты скорости заключается в определении через корреляционную функцию сигнала временного интервала τ₁, в течение которого частица проходит расстояние d₁ между r и g лазерными плоскостями. Совершенно аналогично определяется скорость частицы между g и b лазерными плоскостями:

Равенство скоростей V_z1=V_z2 означает, что на пространственном интервале между r и g плоскостями градиент z-компоненты скорости отсутствует. Если скорости v_z1 и V_z2 не равны, градиент скорости V_z на этом пространственном интервале d₁+d₂ определяется как

Следовательно, предложенный способ позволяет определять и поле компонент скоростей, ориентированных нормально к r, g и b световым плоскостям, сформированным в исследуемой среде. Таким образом, задача расширения функциональных возможностей на измерение 3D поля скоростей в газовых и конденсированных средах решается предлагаемым способом за счет того, что структурированное зондирующее световое поле формируется в исследуемой среде в виде параллельных световых плоскостей на длинах волн, соответствующих цветовой чувствительности пикселей в структуре фотоматрицы, регистрирующей изображения световых плоскостей. Изображения световых плоскостей одновременно формируются на фотоматрице в телецентрической проекции. Эмуляция динамической пространственной фильтрации выполняется на пиксельных структурах, цветовая чувствительность которых согласована с длиной волны соответствующей световой плоскости. Получают корреляционные функции попарных изображений световых плоскостей и определяют пространственное распределение отношения попарного расстояния между световыми плоскостями к временному интервалу между экстремумами в соответствующих корреляционных функциях.

Способ измерения поля скоростей в газовых и конденсированных средах, заключающийся в том, что в исследуемой среде формируют структурированное зондирующее световое поле, изображение которого в рассеянном свете проектируют на фотоматрицу видеокамеры, анализируют изображения путем эмуляции динамической пространственной фильтрации и скорость определяют через частоту фильтрованного сигнала, отличающийся тем, что структурированное зондирующее поле формируют в виде параллельных световых плоскостей на длинах волн, соответствующих цветовой чувствительности пикселей фотоматрицы, изображения световых плоскостей одновременно формируют на фотоматрице в телецентрической проекции, эмуляцию динамической пространственной фильтрации выполняют на пиксельных структурах, световая чувствительность которых согласована с длиной волны соответствующей световой плоскости, получают корреляционные функции попарных изображений световых плоскостей, а поле нормальных к световым плоскостям компонент скорости определяют как пространственное распределение отношения попарного расстояния между световыми плоскостями к интервалам между экстремумами в соответствующих корреляционных функциях.