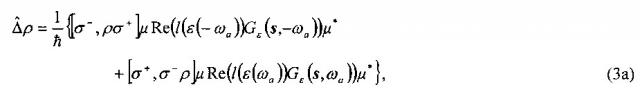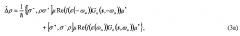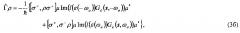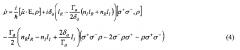Способ подавления спонтанной эмиссии квантовых излучателей в среде с диссипацией

Способ подавления спонтанной эмиссии квантовых излучателей в среде с диссипацией

Иллюстрации

Показать все

Реферат

Изобретение относится к области управления скоростью спонтанной релаксации квантовых излучателей путем их помещения в условиях диэлектрического макроокружения и может быть использовано для хранения и преобразования оптической информации.

Известен способ преобразования длины волны светового излучения за счет эффекта Парселла - управления спонтанными релаксационными процессами для квантовой точки в фотоннокристаллическом микрорезонаторе [«Wavelength conversion device, wavelength conversion method, and single photon generation device», патент JP 2011164127, Igarashi Yuichi, Shirane Masayuki, Application Date 04.02.2010]. Способ основан на поглощении входного излучения, длина волны которого лежит в области фотонной запрещенной зоны, квантовой точкой и последующим его преобразованием в излучение с длиной волны, для которой фотонный кристалл прозрачен. Также известен способ управления динамикой спонтанного излучения для квантовой точки, помещенной в двумерный фотонный кристалл [A. Kress, F. Hofbauer, N. Reinelt, М. Kaniber, Н.J. Krenner, R. Meyer, G. , and J.J. Finley Phys. Rev. В 71, 241304, 2005]. В основе способа лежит блокирование излучения квантовой точкой, резонансная частота которой соответствует фотонной запрещенной зоне кристалла, либо, напротив, увеличение скорости спонтанной эмиссии при равенстве соответствующих частот для квантовой точки и фотонного кристалла.

Недостатками данных способов является то, что они требуют наличия микро- либо наноструктурированного окружения для квантового излучателя, тогда как возможность изменения релаксационных процессов при излучении в однородную сплошную среду не рассматривается.

Известен также способ изменения скорости спонтанного излучения атома, расположенного вблизи тел с размерами меньше длины волны [В.В. Климов, М. Дюклуа, B.C. Летохов, Квантовая электроника, 31, с. 569, 2001]. Способ основан на использовании граничных условий для формирующегося вблизи объектов с малым радиусом кривизны поля, что искажает спектральную структуру мод, в которые может излучать атом и приводит к изменению его скорости спонтанной эмиссии.

Ограничения данного метода связаны со сложностью технической реализации комбинированных структур излучатель-нанообъект и их использования на практике.

Задача, решаемая изобретением - определение возможностей управления развитием релаксационных процессов в однородной среде за счет безрезонаторного, по сравнению с эффектом Парселла, эффекта изменения действующего значения скорости спонтанной релаксации квантовых излучателей.

Предлагаемая задача решается тем, что в способе подавления спонтанной эмиссии квантовых излучателей в среде с диссипацией, включающем взаимодействие поля электромагнитной волны с двухуровневым квантовым излучателем, отличием является помещение излучателя в однородную диэлектрическую матрицу-носитель с комплексным показателем преломления, что позволяет переопределить соотношение для скорости спонтанной релаксации в среде в виде:

где δ_а - величина лэмбовского сдвига, Г_а - скорость излучательной релаксации излучателя в вакууме, есть комплексная функция , для которой , при выборе показателя преломления среды носителя n=n_R+in_I с действительной n_R и мнимой n_I частями.

Технически наблюдение полного подавления (Г_ε=0) спонтанной релаксации возможно для квантовых излучателей в условиях диэлектрического макроокружения при выполнении условия

и в пренебрежении малым параметром лэмбовского сдвига δ_a.

При этом матрица плотности для двухуровневой квантовой точки ρ, возбуждаемой полем Е, подчиняется следующему уравнению в представлении взаимодействия:

где - постоянная Планка, i - мнимая единица; первое выражение в правой части описывает действие поля на квантовую точку, а операторы и определяются следующими выражениями:

в которых σ⁺ и σ^- обозначают экситонные проекционные операторы и представляет оператор дипольного момента с частотой перехода ω_а и матричным элементом перехода μ. При этом функция определяет отношение между локальным и максвелловским Е_M полями, т.е. , а G_ε(s, ω_a) представляет Гриновский тензор электромагнитного поля в среде с проницаемостью ε на частоте ω:

,

,

, , ζ=iqs→0, s=r-r₀, r - текущая координата, r₀ - точка наблюдения, с - скорость света, - единичный оператор.

Вводя следующие обозначения и для операторных выражений скорости спонтанной релаксации и частоты отстройки излучающей моды, может быть получено управляющее уравнение на матрицу плотности вида

на основе которого и получена формула (1).

Пример реализации способа

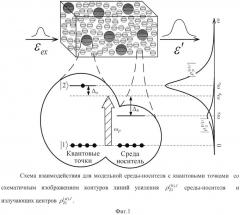
В качестве рабочей среды использовали модель тонкой диэлектрической пластинки, допированной квантовыми точками InSb, схема взаимодействия с внешним полем для которых представлена на Фиг. 1, а параметры взаимодействия составляли: характерный размер квантовых точек 22 нм, длина волны перехода равна 3 мкм, дипольный момент составляет μ=2.43⋅10^-28 К⋅м, действительный показатель преломления среды-носителя n_R=1.4, его мнимая часть n_I=1.15. При выбранных параметрах в диэлектрической среде с квантовыми точками возможно обнуление скорости спонтанной релаксации, как на Фиг. 2.

Способ подавления спонтанной эмиссии квантовых излучателей в среде с диссипацией, включающий взаимодействие поля электромагнитной волны с двухуровневым квантовым излучателем, отличающийся помещением излучателя в однородную диэлектрическую матрицу-носитель с комплексным показателем преломления, что позволяет переопределить соотношение для скорости спонтанной релаксации в среде в виде:

и при соответствующем выборе величин n_R и n_I получить обнуление величины Г_ε, где - величина лэмбовского сдвига, Г_а - скорость излучательной релаксации излучателя в вакууме, есть комплексная функция , для которой , при выборе показателя преломления среды носителя n=nR+inI с действительной nR и мнимой nI частями.