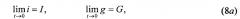Способ определения составляющих импеданса биообъекта

Способ определения составляющих импеданса биообъекта

Иллюстрации

Показать все

Реферат

Изобретение относится к медицине и может быть использовано для оценки функционального состояния организма.

Известен способ измерения электрических величин активного сопротивления, емкости и индуктивности [Авт.св. СССР 1797079, МКИ³ G01R 27/18], согласно которому на последовательную активно-емкостную или активно индуктивную цепь подают напряжение постоянного тока. При этом один элемент цепи известен. После подачи напряжения через определенные промежутки времени At измеряют первое и второе мгновенные значения напряжения на средней точке измерительной цепи. Неизвестные элементы определяют соответственно по формулам для активно-емкостной и индуктивно-емкостной цепей.

Недостаток такого способа измерений сопротивлений в том, что он не позволяет измерить с достаточной точностью значения активной и реактивной составляющих комплексного сопротивления.

По способу определения составляющих импеданса биообъекта [см. Авт.св. СССР №1397024, МПК А61В 5/05, опубл. 1988, Бюл. №19] на биообъект накладывают электроды, через которые подается импульс тока определенной полярности и с амплитудой I₀. Так как составляющая импеданса имеет емкостной характер, происходит переходный процесс нарастания напряжения. В моменты времени t₁ и t₂ измеряют напряжения U₁ и U₂. Измерение в момент t₂ происходит тогда, когда емкость тканей заряжена полностью, т.е. переходной процесс закончился. Величина I₀ выбирается такой, чтобы за время действия импульса тока произошел полный заряд емкости тканей. Тогда напряжение на биообъекте пропорционально величине активной составляющей импеданса биообъекта.

Недостатками являются наличие динамической и методической погрешностей и низкая оперативность, вызванная необходимостью ожидания установившегося режима.

Наиболее близким к заявленному техническому решению является способ определения составляющих импеданса биообъекта [Пат. РФ №2509531, МПК8 А61В 5/05, опубл. 2014, Бюл. №5], заключающийся в том, что на биообъект подается импульс тока Ι₀ и измеряют напряжения в моменты времени t₂=2t₁. По измеренным значениям напряжения и моментам времени регистрируют информативные параметры: потенциал Ε и постоянную времени Т, по которым определяют значение активного сопротивления и эквивалентную емкость тканей биообъекта.

Недостатком прототипа является относительно низкие оперативность и точность способа.

Технической задачей способа является повышение точности и оперативности измерения составляющих комплексного сопротивления биообъекта за счет устранения методической и динамической погрешностей.

Данная техническая задача достигается тем, что в способе определения составляющих импеданса биологического объекта, заключающемся в подаче на биообъект импульса стабилизированного тока I₀ и измерении напряжения и в момент времени t после начала импульса тока в качестве составляющих импеданса биообъекта определяют активное сопротивление R и эквивалентную емкость С тканей биообъекта, в отличие от прототипа дополнительно измеряют в тот же момент времени ток i и поток g, а составляющие импеданса определяют по трем импульсным динамическим характеристикам (ИДХ): ИДХ напряжения (t), ИДХ тока i(t), ИДХ потока g(t), по которым регистрируют параметры ИДХ: установившееся напряжение Ε и постоянную времени Τ=- i/g, а также стабилизированный ток I и поток G как отношения I=Е/Т и G=I/T, по параметрам рассчитывают активное сопротивление R=E/I и эквивалентную емкость С=T/R тканей биологического объекта.

Сущность предлагаемого способа поясняется на фиг. 1 и 2.

На фиг. 1 представлено моделирование исследуемых (t), i_i(t), g_i(t) (графики 1, 3, 5) ИДХ относительно эквивалентов экспериментальных (t), i_э(t),g_э(t) (графики 2, 4, 6) ИДХ. На фиг. 2 представлена оценка адекватности полученных зависимостей по формулам определения относительной погрешности, на примере ИДХ тока i(t) относительно i_э(t).

После включения питающего напряжения на биообъект через электроды подают импульс стабилизированного тока. В момент времени t₁ измеряют значения падения напряжения (см. фиг. 1, график 1), тока i (фиг. 1, график 3) и потока g (фиг. 1, графики 5). По измеренным значениям через установившееся значение потенциала Ε и постоянную времени Τ находят активное сопротивление и эквивалентную емкость.

Зависимость (1) связывает между собой измеряемое значение амплитуды U напряжения за время t исследования до установившегося значения Ε потенциала с постоянной времени Т

где Ε и Τ (фиг. 1, графики 7 и 8) служат оптимальными параметрами ИДХ, однозначно определяющими ИДХ (фиг. 1, графики 1) напряжения (1), т.к. являются предельными значениями переменных напряжения U и времени t. Предельные значения отражают физические закономерности

которые следуют из ИДХ (1) и однозначно определяют физику процесса, т.к.

ИДХ U(t)= , I(t)=i, G(t)=g (фиг. 1, графики 3 и 5) меняются по законам

Значение напряжения U(t)= определяется (см. фиг. 1, график 2) первообразной импульсной динамической характеристикой (1), представленной дифференциальным уравнением первого порядка

Значение ИДХ тока I(t)=I определяется (фиг. 1, график 4) как первая производная от ИДХ напряжения (2)

а значение потока G(t)=g (фиг. 1, график 6) определяется как первая производная от тока (3), а именно

Алгоритм параметра Τ (фиг. 1, график 8) постоянной времени определяют из формулы (3) при подстановке в нее выражения (2)

Следовательно, алгоритм (5) оптимизации постоянной времени регламентирован отношением измеренных в заданный момент времени значений тока и потока (скорости изменения тока).

Параметр Ε (фиг. 1, график 7) установившегося значения находят подстановкой алгоритма (5) в уравнение (2)

Следовательно, алгоритм (6) оптимизации установившегося значения регламентирован алгебраической суммой напряжения и отношением измеренных в заданный момент времени значений квадрата тока и потока.

После нахождения информативных параметров определяется значение активного сопротивления

Это обусловлено значением тока

В начальный момент времени t=0, когда e=1

где начальный ток I_н тождественен амплитуде стабилизированного тока I.

Значение тока I(t)=i, а значение потока G(t)=g, из чего следует тождественность отношения переменных отношению параметров, а именно

Зависимость (8) отражает закономерности параметров ИДХ при t=0

которые следуют из ИДХ (3-4) и однозначно определяют физику процесса, т.к.

Если в зависимость (3) подставить в формулу (1), то в начальный момент времени t=0 получим выражение для начального тока

Эквивалентная емкость тканей биообъекта в свою очередь определяется как

Адекватность и эффективности по точности предлагаемого способа представлены ниже.

1. Адекватность предлагаемого способа физике эксперимента доказывает математическое моделирование исследуемых (t), i_i(t), g_i(t) (фиг. 1, графики 1, 3, 5) ИДХ относительно эквивалентов экспериментальных u₃(t), U(t), g₃(t) ИДХ (фиг.1, графики 2, 4, 6). По полученным значениям R и С определяется значение периода T (согласно формуле T=R⋅C), строятся исследуемые 1, 3, 5 и эквивалентные 2, 4, 6 ИДХ (фиг. 1).

Затем проводится оценка адекватности полученных зависимостей по формулам определения относительной погрешности

ИДХ тока i(t) относительно i_э(t) не превышает 2,5⋅10^-9% (см. фиг. 2), аналогично ИДХ напряжения (t) относительно u_э(t) не превышает 2⋅10^-13 %

соответственно ИДХ потока g(t) относительно g_э(t) не превышает - 6⋅10^-9%

Тождественности исследуемых (t), i_i(t), g_i(t) (фиг. 1, графики 1, 3, 5) ИДХ эквивалентам (t), i_э(t), g_э(t) ИДХ (фиг. 1, графики 2, 4, 6) с минимальной относительной погрешностью (фиг. 2) подтверждает адекватность способа физике эксперимента.

2. Оценка метрологической эффективности способов по точности приведена на примере экспериментальных (t), i_э(t), g_э(t) ИДХ (фиг. 1, графики 2, 4, 6) с параметрами Т=42⋅10^-7 с, Ε=120 мВ, I=Е/Т=2,857⋅10⁴А и G=Ι/Τ=6,803⋅10⁹ А/с.

Работоспособность предлагаемого способа доказывает оценка методической погрешности ε для любых заданных моментов времени t_i и измеренных значений ИДХ напряжения тока i_i и потока g_i (фиг. 1, графики 1, 3, 5). Зададим, например, моменты времени t_i кратно постоянной времени: 0.1, 0.5, 1, 3, 5T, - результаты измерений ИДХ систематизируем в табл. 1. Для i-х измерений по алгоритмам (3-5) рассчитаем предельные параметры T_i (5) и E_i (6), I_i (9) и G_i (5, 8), с помощью которых восстановим по формулам (2)-(4) ИДХ (фиг. 1, графики 2, 4, 6). Методическую погрешность оценим по тождественности откалиброванных характеристик (фиг. 1, графики 1, 3, 5) экспериментальным эквивалентам (фиг. 1, графики 2, 4, 6).

Анализ табл. 1 показывает тождественность откалиброванных характеристик эквивалентам, что подтверждают тождественности рассчитанных параметров T_i и E_i, I_i и G_i заданным эквивалентам Τ и Ε, I и G, а также нулевые погрешности параметров, т.е. исключение методической погрешности, подтверждающей работоспособность способа.

3. Оценку динамической погрешности ε проведем для любых заданных моментов времени t₂=2t₁ и параметров Τ, Ε, Ι. Зададим, например, моменты времени t₁ кратно постоянной времени 0,1Τ=10⋅10^-7 с, соответственно, момент времени t₂=0,2Т=20⋅10^-7 с (см. табл. 2, 2 строка). На практике моменты времени t_1i и t_2i следуют с отклонением от теоретического эквивалента соответственно -5, -2, -1, +5%. Теоретические значения в моменты времени t₁ и t₂ являются идеальными, так как их отношения кратно 2, а на практике отклонения теряют эту кратность. Результаты измерений систематизируем в табл.2. Для i-х измерений по выше представленным алгоритмам рассчитаем напряжения U_1ш и U_2i, предельные параметры T_i и E_i, I_i. Динамическую погрешность оценим по сравнению последующих значений характеристик с идеальным эквивалентом.

Анализ табл. 2 показывает, что отклонения измеренных напряжений прототипа приводят к большой динамической погрешности параметров ИДХ относительно нулевой погрешности теоретических значений, что доказывает эффективность предлагаемого способа.

4. Практическую значимость предлагаемого решения доказывают тождественности исследуемых сопротивления и емкости импеданса биообъекта их действительным значениям эксперимента с минимальной погрешностью (см. табл. 3).

5. Повышение оперативности предлагаемого способа оценивается эффективностью времени измерения t. Для прототипа значение времени t₂=2t₁≤Т. В предлагаемом способе t₁≤Т/2.

Находим эффективность, а именно η_t

Из полученного значения эффективности следует, что оперативность предлагаемого способа не менее чем в два раза выше известных способов.

Таким образом, определение активной и реактивной составляющих комплексного сопротивления по информативным параметрам трех динамических характеристик в один момент времени в отличие от известных решений повышает точность определения составляющих импеданса биологического объекта на несколько порядков за счет адекватности предлагаемого способа эксперименту при отсутствии методической и динамической погрешностей.

Способ определения составляющих импеданса биологического объекта, заключающийся в подаче на биообъект импульса стабилизированного тока I и измерении напряжения и в момент времени t после начала импульса тока в качестве составляющих импеданса биообъекта определяют активное сопротивление R и эквивалентную емкость С тканей биообъекта, отличающийся тем, что дополнительно измеряют в тот же момент времени ток I и поток g, а составляющие импеданса определяют по трем импульсным динамическим характеристикам (ИДХ): ИДХ напряжения u(t), ИДХ тока i(t), ИДХ потока g(t), по которым регистрируют параметры ИДХ: установившееся напряжение Е и постоянную времени T=-i/g, а также стабилизированный ток I и поток G как отношения I=Е/Т и G -I/T, по параметрам рассчитывают активное сопротивление R=E/I и эквивалентную емкость C=T/R тканей биологического объекта.