Способ одновременной калибровки трех и более однотипных устройств с измерительными функциями без опоры на эталонное устройство или эталонный испытательный сигнал

Способ одновременной калибровки трех и более однотипных устройств с измерительными функциями без опоры на эталонное устройство или эталонный испытательный сигнал

Иллюстрации

Показать все

Реферат

Изобретение относится к метрологии, приборостроению, навигационному приборостроению и другим областям, использующим в том или ином виде измерительную технику, в частности к способам калибровки средств измерений (далее - СИ) с целью оценивания их показателей точности, где термины «калибровка», «СИ» и «показатель точности» определены в [1]. При этом процедура калибровки СИ рассматривается в данном изобретении не в полном объеме, а только в части количественного оценивания его точностных характеристик, в том числе с целью подтверждения их соответствия установленным требованиям, не включая при этом задачу метрологической прослеживаемости результатов измерений к эталону [1].

Помимо СИ, изобретение может быть применено к любым техническим системам и устройствам с измерительными функциями (далее - ТСУИФ [2]), включая случай недопустимости демонтажа их измерительной части (для проведения калибровки), если он может повлечь за собой нарушение целевых функций указанных систем. Изобретение может быть применено также в области технологической подготовки и сопровождения различных производств с использованием СИ и ТСУИФ при необходимости выполнения их аттестации и процедур подтверждения соответствия, в том числе для случаев непосредственного применения СИ и ТСУИФ (в ходе указанного сопровождения) и при их вхождении в состав имеющихся автоматизированных систем управления технологическими процессами. Изобретение может быть применено также к испытаниям готовой продукции, содержащей в своем составе ТСУИФ, с целью подтверждения соответствия характеристик их измерительной части установленным требованиям. Изобретение позволяет также обеспечить возможность выполнения самодиагностики измерительных компонентов (при их наличии) различных систем, включая и автономные системы.

Примерами подобных СИ и ТСУИФ (далее - устройств) могут служить такие устройства как курсоуказатель и лаг (входящие в состав инерциальной навигационной системы), волномерный буй (регистрирующий текущие параметры морского волнения в составе системы стабилизации морской платформы), а также ряд других устройств, для которых актуальна задача локальной калибровки, состоящая в оценивании показателей их реальной точности. Для решения указанной задачи функциональное представление об устройстве принято в виде, представленном на фиг. 1.

На указанной фиг. 1 обозначены:

- «объект» - элемент некоторой внешней (по отношению к устройству) системы естественного или искусственного происхождения, который необходимо контролировать (или изучать) с помощью устройства;

- Q(t) - переменный входной сигнал, воздействующий на чувствительный элемент устройства, который порождается интересующим нас фактором объекта и который поставлен в соответствие измеряемой физической величине, где последняя традиционно понимается как некоторый параметр принятого модельного представления об объекте [1];

- S(t) - выходной сигнал (показание) устройства, принимаемый за результат измерения;

- t - текущее время.

При этом точность устройства может быть охарактеризована теми или иными параметрами его погрешности ξ(t)=S(t)-Q(t) [3]. Указанные параметры погрешности уточняются ниже и подлежат оцениванию в ходе калибровки, которую необходимо выполнить с целью обоснования возможности использования результата измерения S(t) по назначению.

Конкретизируем ряд аспектов устройств, калибруемых в соответствии с данным изобретением. Прежде всего, предполагается, что каждое из этих устройств имеет функцию записи на магнитный носитель (в файл на диске) своих дискретных показаний S_i=S(t_i) в моменты времени t_i=t₀+(i-1)⋅Δt, следующие с некоторым периодом дискретизации Δt, где t₀ - момент начала записи, i=1,2,…,n - номер показания, n - длина записанной реализации. При этом, учитывая, что погрешность ξ(t), которой отягощен выходной сигнал S(t), имеет случайную составляющую, предполагается, что период дискретизации Δt выбран не меньшим, чем время автокорреляции выходного сигнала S(t) для каждого из этих устройств. Предполагается также, что запись данных от всех устройств выполняется синхронно, в том числе, с одинаковым периодом дискретизации Δt. Для целей дальнейшего изложения введем также сокращенные обозначения Q_i=Q(t_i), ξ_i=ξ(t_i), аналогичные S_i.

Кроме того, считаем, что в соответствии с [1, 2] конструкторская и технологическая проработка при создании каждого из рассматриваемых устройств выполнена на должном, достаточно высоком уровне. В том числе, предполагаются выявленными и изученными все дополнительные факторы, влияющие на выходной сигнал S(t), после чего обеспечена либо стабилизация этих факторов, либо автокомпенсация соответствующих систематических искажений выходного сигнала S(t) на аппаратном или программном уровне. К числу таких факторов, прежде всего, следует отнести климатические, механические, электромагнитные факторы (температуру, давление, влажность, уровень вибраций, помехи по электропитанию и т.п.), а также ряд других более специфических факторов, таких как параметры качки и движения морских объектов для приведенных выше примеров устройств.

В этих предположениях погрешность ξ(t) каждого из рассматриваемых устройств может быть описана чисто стохастической стационарной моделью. При этом для сохранения стационарности указанной модели дополнительно сделаны следующие предположения общего вида в отношении входного сигнала Q(t):

(а) Q(t)∈[Q_min,Q_max] - ограниченность диапазона возможных значений сигнала;

(б) ⎪dQ(t)/dt⎪<<ΔQ/Δt - плавность изменения сигнала, где ΔQ=Q_max-Q_min.

Это позволяет пренебречь динамической составляющей погрешности устройства, обусловленной резкими изменениями входного сигнала Q(t), и считать стохастическую модель погрешности ξ(t) стационарной на протяжении всего времени наблюдения за объектом. Кроме того, используется обычное в подобных случаях предположение об эргодичности [4] модели погрешности, позволяющее заменить усреднение по ансамблю выходных сигналов S(t) на усреднение по времени одной реализации указанного сигнала.

На основании сказанного, в предлагаемом изобретении предполагается следующая модель дискретного выходного сигнала {S_i} (i=1,2,…,n) каждого устройства:

где Q_i - текущее значение входного сигнала (измеряемой величины), а погрешности {ξ_i} предполагаются случайными величинами, которые одинаково распределены с первыми двумя постоянными моментами {а, σ²} и попарно некоррелированны: cov(ξ_i,ξ_j)=0 при i≠j. В этом модельном представлении указанные параметры считаются неизвестными и понимаются как остаточный сдвиг нуля устройства а и среднее квадратическое отклонение σ (далее - СКО) его случайной погрешности. Свои конкретные значения указанные параметры получают в ходе необходимой предварительной регулировки каждого устройства в соответствии с [1], а также процедуры его включения и выхода на рабочий режим. Регулировка устройства в простейшем случае состоит в устранении сдвига нуля его показаний (в максимально возможной степени) и уточнении коэффициента усиления во всем диапазоне показаний устройства, а с учетом сказанного выше о компенсации основных систематических искажений выходного сигнала можно считать выполненным условие |а|<<σ.

Таким образом, в описанных выше условиях основным показателем точности устройства является параметр σ - СКО случайной составляющей его погрешности, и задача калибровки устройства понимается в данном изобретении как получение оценки гарантированного качества, где степень качества оценки, как обычно, характеризуется двумя параметрами: ее смещением и дисперсией [5]. Здесь и далее E(…) и D(…) обозначают, соответственно, операторы математического ожидания и дисперсии, применяемые к случайным величинам, в том числе, и к оценкам, вычисляемым по экспериментальным данным. Кроме того, в обоснованных случаях вместо указанных параметров и используются их безразмерные аналоги, обозначаемые ниже, как и .

В частности, если калибруемое устройство является СИ, в отношении которого в установленном порядке были проведены испытания с целью утверждения типа с последующим внесением в Госреестр СИ [6], то его калибровка в рассмотренных выше предположениях об устройстве и в части оценивания его точностных характеристик по содержанию будет практически совпадать с процедурой поверки этого СИ, отличаясь лишь юридическим статусом результатов.

Известные способы и процедуры калибровки (поверки) устройств рассматриваемого вида изложены в целом ряде монографий, руководств и методических материалов по метрологии, включая нормативные документы [7-9]. При этом, несмотря на некоторые различия и разную степень детализации в описании указанных процедур, все известные источники предполагают обязательное использование образцового (эталонного) предварительно аттестованного устройства, точность которого не только предполагается известной (либо нормированной, например, своей верхней предельно допустимой границей СКО σ_max), но также и существенно превосходящей предполагаемую точность калибруемого устройства. Указанное требование значительно ограничивает область применения известных способов калибровки, которые, как правило, должны выполняться в аттестованных лабораториях, имеющих метрологический статус, а также с привлечением специализированных устройств и оборудования.

Наиболее близким по технической сущности и принятым за прототип является известный способ калибровки устройства [10, §56]. Известна также детализация указанного способа-прототипа для рассматриваемого случая доминирования случайной погрешности [11, раздел 10-2]. Хотя формально способ-прототип [10, 11] описывает способ поверки СИ, его очевидным образом можно распространить и на способ калибровки (в указанном выше смысле) измерительной части любого ТСУИФ. Способ-прототип основан на использовании, помимо калибруемого устройства (далее - КУ), еще одного дополнительного устройства (однотипного с КУ по входному сигналу), которому придается статус образцового или эталонного устройства (далее - ЭУ). Сущность способа-прототипа представлена на фиг. 2, поясняющей, что входной сигнал Q(t) подают одновременно на входы обоих устройств КУ и ЭУ, с последующим сравнением их показаний S^K(t) и S^Э(t), где верхние индексы означают принадлежность к соответствующему устройству. Указанное пояснение касается также дополнительных индексов в обозначениях других используемых ниже переменных.

При этом входной сигнал Q(t) играет роль испытательного, и его формируют, как правило, с помощью специального генератора, поочередно задавая значения Q(t) таким образом, чтобы охватить все заранее предписанные точки диапазона КУ. В этом смысле калибровка устройства согласно способу-прототипу является активным экспериментом. Следует также отметить, что допустимо совмещение функций генератора и ЭУ в одном устройстве, что не меняет сути способа-прототипа.

Важно отметить, что точность ЭУ предполагается известной и существенно (в несколько раз) превышающей ожидаемую точность КУ, о которой судят на основе имеющейся априорной информации, например, по паспортным данным КУ. Таким образом, в принятых обозначениях базовое требование способа-прототипа имеет вид:

где σ_Э и σ_К - СКО случайной погрешности ЭУ (либо известно, либо нормировано) и КУ (подлежит оцениванию), k - коэффициент запаса по точности ЭУ. При этом на практике выбирают k≈3 [10, 11], однако в ряде специфических областей измерений указанный коэффициент лежит в более широких границах 1,5<k<10 [9].

Обработка данных {S_i^К}, {S_i^Э} (i=1,2,…,n) сводится к вычислению последовательности попарных разностей {ΔS_i} показаний, а затем их выборочной дисперсии D_S:

где для несмещенности D_S согласно [5] использован коэффициент 1/(n-1). Далее, в силу тождественного соотношения ΔS_i=S_i^К-S_i^Э=ξ_i^К-ξ_i^Э и некоррелированности показаний разных конструктивно независимых устройств верно выражение:

Окончательно, отбрасывая в (4) второе слагаемое, что возможно в силу требования (2), получаем следующую оценку искомого параметра σ_K по способу-прототипу:

В части анализа качества указанной оценки в способе-прототипе найдена только верхняя граница ее относительного смещения , а именно, при k≥3 установлено, что [10, 11]. К этому следует добавить, что оценка очевидным образом является завышенной: . В то же время, сведения о дисперсии , характеризующей диапазон возможного случайного разброса реализаций этой оценки, ни в способе-прототипе, ни в других известных источниках не приводятся.

Недостатками способа-прототипа являются:

1) необходимость использования дополнительного ЭУ с известной и существенно более высокой (в несколько раз) точностью по сравнению с КУ;

2) отсутствие анализа качества оценки в части ее дисперсии;

3) ориентированность на выполнение активного эксперимента с применением специального генератора, формирующего требуемые значения входного сигнала Q(t).

Вследствие недостатков способа-прототипа его применение ограничено. Он может быть использован лишь в метрологических лабораториях, осуществляющих контроль СИ на стационарных установках, ключевыми элементами которых являются аттестованное эталонное (образцовое) СИ и генератор испытательных сигналов. Что же касается ТСУИФ, то для применения способа-прототипа к их измерительной части необходимы либо возможность ее демонтажа (без нарушения целевых функций ТСУИФ), либо наличие мобильного варианта аттестованного эталонного устройства; при этом на практике и то, и другое далеко не всегда доступно. Кроме того, анализ качества оценки по способу-прототипу не выполнен полностью: показано лишь малое смещение этой оценки (при k≥3), что вовсе не гарантирует ее малого случайного разброса, который возможен и в сторону значительного занижения оценки .

Вместе с тем, существует ряд областей использования СИ и ТСУИФ с подтвержденной моделью выходных сигналов (1), для которых чрезвычайно существен был бы оперативный, проводимый на месте контроль их точности (стабильности) вне зависимости от наличия эталонного устройства. В качестве примера можно привести процедуры аттестации и подтверждения соответствия в области технологической подготовки и сопровождения различных производств в части СИ и ТСУИФ, входящих в состав имеющихся автоматизированных систем управления технологическими процессами, а также аналогичные процедуры, используемые при испытаниях готовой продукции с ТСУИФ в своем составе и ориентированные на проверку их измерительных характеристик. Это касается также возможности различных систем выполнять самодиагностику своей измерительной части (при ее наличии), и, в особенности, - поддержания работоспособности различных автономных систем, что необходимо при функционировании космической, подводной и подземной (скважинной) аппаратуры, при геодезических работах, проводимых в удаленных районах, и т.п.

К этому же типу можно отнести ряд собственно метрологических задач, особенностью которых является одновременное исследование нескольких однотипных СИ с целью их аттестации и взаимного сопоставления по точности в условиях отсутствия (или ограниченной доступности) более точного СИ. Это имеет место, например, при создании и эксплуатации групповых эталонов разных уровней, а также при проведении круговых сличений национальных и международных первичных эталонов.

Задача, которая решается предлагаемым изобретением, заключается в увеличении области применения способа калибровки (поверки) рассматриваемых устройств.

Технический результат предложенного способа калибровки состоит в расширении границ области применения способа путем отказа от использования дополнительного эталонного устройства, имеющего известную и более высокую точность, а также в получении гарантированных оценок достоверности результатов калибровки и их повышенной эффективности по сравнению со способом-прототипом. Предложенный способ позволяет также полностью отказаться от использования специального генератора, формирующего необходимые значения входного сигнала.

Задача решается путем использования, помимо исходного КУ, калибровку которого требуется выполнить изначально, двух или более дополнительных устройств, которые также предназначены для измерения той же самой величины Q, однако ни одному из них не придается эталонный статус, в том числе могут отсутствовать предварительные оценки их показателей точности. Это означает, что все устройства - и исходное калибруемое, и дополнительные - являются равноправными при калибровке. Другими словами, процедура калибровки по предлагаемому способу организуется как проводимая одновременно для всех участвующих в ней устройств, для которых в связи со сказанным будем далее использовать симметричные обозначения КУ-1, КУ-2, КУ-3 и т.д. В качестве показателей точности этих устройств, как и ранее, принимаем СКО случайной составляющей погрешности каждого КУ, которые обозначим соответственно σ₁, σ₂, σ₃ и т.д., причем все они считаются неизвестными и подлежат оцениванию. При этом важно, что не накладывается никаких ограничений на соотношения этих параметров между собой: они могут быть как приблизительно попарно равными, так и значительно отличаться друг от друга. Конструктивно одновременно калибруемые устройства могут иметь сходство между собой (в том числе, быть несколькими экземплярами одного серийно выпускаемого устройства), или же принципиально различаться. Единственным обязательным требованием к каждому из устройств является соответствие модели его выходного сигнала соотношению (1), включая и соответствие всем аспектам обоснования этой модели.

Важно также, что для формирования входного сигнала Q(t) не требуется специальный генератор, поскольку калибровка по предлагаемому способу может выполняться в ходе оперативного наблюдения за контролируемым объектом (см. фиг. 1).

Обозначим через m общее количество участвующих в одновременной калибровке устройств. В зависимости от m предлагаемое изобретение может быть реализовано в двух модификациях:

1) минимальный (безызбыточный) случай, при m=3;

2) избыточный случай, при m>3.

При этом вторая модификация отличается от первой лишь несколько более сложным алгоритмом обработки данных.

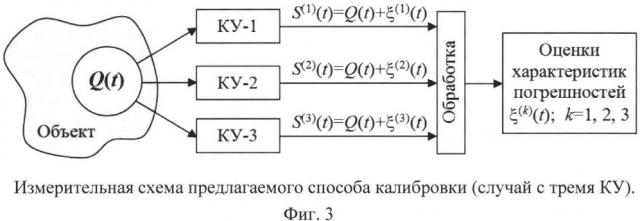
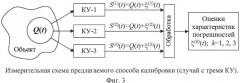
Для минимального случая сущность предлагаемого способа поясняет фиг. 3, на которой показано, что входной сигнал Q(t) подают одновременно на входы всех трех устройств, с последующим сравнением их показании S⁽¹⁾(t), S⁽²⁾(t), S⁽³⁾(t).

Согласно модели (1) дискретных сигналов (i=1,2,…,n; j=1,2,3), их случайные погрешности удовлетворяют следующим условиям: ; при i₁≠i₂ и j,k∈{1,2,3}, а также при i₁=i₂ и j≠k, где параметры неизвестны. Обработка данных на первом этапе аналогична таковой для способа-прототипа, а именно: вычисляются последовательности разностей показаний выходных сигналов во всех сочетаниях их пар:

а затем - выборочные дисперсии этих последовательностей:

где индексы j,k∈{1,2,3} выбирают в соответствии с (6), a - средние значения разностей (6). При этом для каждой из трех выборочных дисперсий (7) остается в силе соотношение, аналогичное (4):

Однако, в отличие от способа-прототипа, имеется уже не одно уравнение (4) с двумя неизвестными, а система трех линейных уравнений (8) относительно интересующих нас трех параметров . Очевидным решением системы (8) являются оценки:

В отношении найденных оценок необходимо отметить следующие два важных аспекта. Во-первых, каждая из выборочных дисперсий (7), и, как следствие, система (8) в целом инвариантна относительно неизвестных остаточных сдвигов нулей {a_j} калибруемых устройств, даже если они не являются малыми на фоне оцениваемых СКО {σ_j}. Это существенно ослабляет исходные требования к калибруемым устройствам. Во-вторых, выборочные дисперсии (7), являющиеся правыми частями системы (8), содержат преобразованные случайные погрешности , входящие в исходные данные . Более того, в силу соотношений (6) выборочные дисперсии (7) являются взаимно коррелированными. Эти факты могут привести к существенному ухудшению достоверности полученных результатов (9), вплоть до потери ими физического смысла. А именно, путем моделирования по известному методу Монте-Карло [12] было получено, что при умеренной длине реализаций n<1000 имеется значимо отличная от нуля вероятность того, что наименьшая из трех оценок окажется отрицательной. Указанная вероятность тем больше, чем меньше n и чем существеннее различие оцениваемых параметров между собой. Таким образом, ключевым вопросом возможности применения предлагаемого способа калибровки является анализ качества оценок , который и выполнен далее.

Прежде всего, оценки являются несмещенными, что следует из известного факта несмещенности выборочных дисперсий (7) [5] и линейности системы (8). Таким образом, главными и единственными параметрами качества оценок являются их дисперсии , характеризующие возможный случайный разброс оценок . Оценить эти дисперсии можно одним из двух способов, в зависимости от имеющейся в наличии априорной информации о виде функций распределения погрешностей устройств.

Первый из двух указанных способов применим, если допустимо считать эти функции распределения нормальными, что часто имеет место па практике. В этих предположениях были получены аналитические выражения для теоретических дисперсий оценок путем прямых преобразований соотношений (6)-(9). Опуская промежуточные громоздкие выкладки, приведем только результирующие выражения:

где n - длина реализаций , а слагаемое O(n^-2) означает величину того же порядка малости, что и n^-2. В частности, при наличии информации об ориентировочных значениях параметров (хотя это и не предполагается обязательным в рассматриваемом изобретении) па основе (10) можно получить априорные оценки дисперсий оценок уже на этапе подготовки к проведению одновременной калибровки устройств. В общем же случае, после подстановки оценок в выражения (10) и выполнения ряда тождественных преобразований, можно получить следующие апостериорные оценки искомых дисперсий:

где n - длина реализаций , а выборочные дисперсии и оценки вычислены по (7), (9). При этом на практике удобнее от оценок дисперсий перейти к оценкам СКО , получаемым извлечением квадратных корней из . Одновременно с переходом к целесообразно преобразовать выражения (11) в относительную (безразмерную) форму указанного выше вида :

где все параметры определены в (11). Полученные формулы (12) позволяют сделать обоснованный вывод об уровнях достоверности каждой из трех оценок по отдельности. При этом целесообразно применять следующую ориентировочную шкалу указанных уровней:

1) если оказалось, что , то оценка недостоверна; необходимо увеличить n и повторить эксперимент, с контролем всех требований модели (1) и в первую очередь - условия стационарности погрешностей;

2) при оценка является грубым приближением СКО σ_k;

3) при оценка адекватна интересующему нас СКО σ_k.

Приведенные выше ориентировочные граничные значения (0,5 и 0,05) уровней достоверности могут быть изменены в зависимости от назначения калибруемых устройств. Кроме того, возможна ситуация, когда одна из трех оценок - а именно наименьшая из трех - окажется недостоверной, и, одновременно с этим, одна или обе из оставшихся оценок будут признаны достоверными. Это позволяет ограничить результаты калибровки по предлагаемому способу только одним или двумя из трех устройств, если они интересуют нас в первую очередь. В то же время, как следует из (12), возможно также и одновременное повышение уровня достоверности всех трех оценок , пропорционально (по крайней мере, до тех пор, пока сохраняется стационарность погрешностей всех участвующих в калибровке устройств).

Второй способ оценивания дисперсий оценок требует значительных объемов вычислений, и применять его следует при отсутствии априорной информации о виде указанных функций распределения, а также, если имеются основания сомневаться в их нормальности. Он использует известную процедуру «jack-knife» («складной нож») [12], относящуюся к группе методов так называемого численного ресэмплинга, и состоит в следующем. Среди множества i∈{1,2,…,n) всех номеров показаний фиксируют небольшую долю р этих номеров i∈{i₁,i₂,…,i_[pn]}, где р∈[0,001; 0,05], а запись [pn] означает целую часть числа pn. При этом указанные номера выбирают случайным образом, и показания с этими номерами отбрасывают (блокируют). Для оставшихся троек показаний в количестве n’=n-[pn] выполняют обработку данных согласно (6)-(9), фиксируя полученные оценки , после чего отброшенные данные возвращают обратно. Указанную процедуру со случайным прореживанием данных многократно повторяют (число повторений М>10³), каждый раз заново генерируя номера отбрасываемых показаний. Полученные варианты оценок стандартным образом усредняют и оценивают их дисперсии (по формулам, аналогичным (7)). По этим дисперсиям уже судят о достоверности усредненных оценок аналогично (11) и (12). При повышенных требованиях к достоверности процедуру оценивания этим способом целесообразно повторить для нескольких различных долей р временно отбрасываемых данных, чтобы убедиться в стабильности всех получаемых оценок; можно также увеличить число повторений М до 10⁴ и более.

Перейдем к описанию избыточного случая m>3 предлагаемого способа калибровки. Как уже отмечалось, в процедурном плане он не отличается от минимального случая m=3. А именно, входной сигнал Q(t) подают одновременно на входы всех m устройств, с последующим сравнением их показаний S^(j)(t), j∈{1,2,…,m}. Обработка полученных дискретных данных на первом этапе аналогична (6), (7) с единственным отличием, что в этом случае число всевозможных попарных разностей выходных сигналов будет превышать их количество m. Из этого следует, что система, аналогичная (8), будет избыточной. С учетом отмеченной выше коррелированности правых частей указанной системы, известным стандартным способом ее решения является обобщенный метод наименьших квадратов (далее - ОМНК) [5]. При этом особенностью применения ОМНК (также известной) является возможность получения апостериорных оценок дисперсий получаемых оценок , j∈{1,2,…,m), что автоматически решает проблему оценивания их достоверности.

Исходя из изложенного, заявленная совокупность признаков позволяет получить способ одновременной калибровки (понимаемой в указанном выше смысле) трех и более устройств с измерительными функциями, являющихся однотипными по измеряемой величине, в условиях отсутствия эталонного устройства или эталонного испытательного сигнала.

В качестве первого примера конкретной реализации предлагаемого способа возьмем случай одновременной калибровки трех приблизительно равных по точности устройств (например, являющихся несколькими экземплярами серийно выпускаемого устройства) с соотношением СКО случайной составляющей их погрешностей σ₁:σ₂:σ₃≈1:1:1. В этой ситуации, как следует из формул (10)-(12), удовлетворительные оценки всех трех параметров (они также будут приблизительно равноточными) получаем, начиная уже с n=500, что является реально достижимом на практике. При этом важно, что предлагаемый способ калибровки не опирается на указанный выше факт приблизительного равенства оцениваемых СКО и, более того, позволяет его проверить по завершении калибровки и получении адекватных оценок .

Вторым примером может служить одновременная калибровка трех устройств с соотношением по точности σ₁:σ₂:σ₃≈3:1:1, где первое устройство является основным (интересующим нас в первую очередь), а два других - дополнительными, но которые приблизительно втрое точнее основного. В этой ситуации удовлетворительные оценки основного параметра σ₁ могут быть получены, начиная с n=223 (но при этом оценки вспомогательных параметров σ₂, σ₃ остаются весьма грубыми: , k=2,3). Если же нас интересуют адекватные оценки всех трех параметров, то следует обеспечить n>2100, что также реально достижимо на практике.

Наконец, в качестве третьего примера возьмем ситуацию, обратную предыдущей: пусть требуется выполнить одновременную калибровку трех устройств с соотношением по точности σ₁:σ₂:σ₃≈1:3:3, где первое устройство опять является основным, а два других - дополнительными, но которые на этот раз приблизительно втрое хуже по точности основного. В этой ситуации также можно получить удовлетворительные оценки основного параметра σ₁, но уже при достаточно жестком условии n>10100, что может потребовать дополнительных усилий для обеспечения стационарности погрешностей калибруемых устройств на протяжении всего времени измерений, длительность которого зависит от периода съема данных Δt и может лежать в диапазоне от нескольких минут до нескольких часов (и шире).

При этом нетрудно видеть, что в условиях второго примера способ-прототип, хотя и может быть формально применен, однако без гарантированных оценок достоверности получаемых результатов. В условиях первого и третьего примеров способ-прототип принципиально не допускает применения. Более того, следует обратить внимание на ставшее традиционным широко распространенное мнение, что аттестовать показатели точности измерительного устройства без обязательной опоры на более точное (эталонное) устройство невозможно. Однако предлагаемый способ позволяет успешно решить, в том числе, и подобную задачу.

Работоспособность предлагаемого способа калибровки проверена на практике с помощью одновременных лабораторных испытаний трех экземпляров высокоточного частотомера CNT-90 (изготовитель Pendulum Instruments АВ, Швеция) путем многократных параллельных измерений ими несущей частоты различных кварцевых генераторов (в том числе, низкостабильных, существенно зависящих от температуры и других факторов). Полученные с помощью предлагаемого способа достоверные оценки СКО случайных погрешностей испытуемых приборов позволили не только подтвердить их соответствие своим паспортным данным, но и выполнить их индивидуальное ранжирование по этому показателю и выбрать наиболее точный из трех приборов. Таким образом, фактически была выполнена поверка указанных приборов (в части оценивания СКО их случайных погрешностей), однако при этом не потребовались дорогостоящие еще более точные эталонные (образцовые) приборы.

Источники

1. РМГ 29-2013 «ГСИ. Метрология. Основные термины и определения».

2. ГОСТ Р 8.674-2009 «ГСИ. Общие требования к средствам измерений и техническим системам и устройствам с измерительными функциями».

3. МИ 1317-2004 «ГСИ. Результаты и характеристики погрешности измерений. Формы представления. Способы использования при испытаниях образцов продукции и контроле их параметров».

4. А.М. Яглом. Введение в теорию стационарных случайных функций. - УМН, 1952, том 7, выпуск 5(51), с. 3-168.

5. Г. Крамер. Математические методы статистики. - М.: Мир, изд. 2-е, стер., 1975. - 648 с.

6. www.vniims.ru/inst/gosreestr.html

7. Бурдун Г.Д., Марков Б.Н. Основы метрологии. - М.: стандартов, 1975. - 336 с.

8. Асташенков А.И., Немчинов Ю.В., Лысенко В.Г. Теория и практика поверки и калибровки. - М.: Изд-во стандартов, 1994. - 142 с.

9. Сергеев А.Г., Крохин В.В. Метрология: Учеб. пособие для вузов. - М.: Логос, 2001. - 408 с.

10. Маликов М.Ф. Основы метрологии. - М.: Изд-во Коммерприбор, 1949. - 480 с.

11. Рабинович С.Г. Погрешности измерений. - Л.: Энергия, 197