Способ измерения сверхмалых угловых скоростей

Способ измерения сверхмалых угловых скоростей

Иллюстрации

Показать все

Реферат

Способ измерения сверхмалых угловых скоростей относится к гироскопии и может быть использован для измерения сверхмалых угловых скоростей в космическом пространстве.

Из работ [Бычков С.И., Лукьянов Д.П., Бакаляр А.И. Лазерный гироскоп. Под ред. проф. С.И. Бычкова. Москва: Сов. радио, 1975. - 424 с.] известен способ измерения угловой скорости с использованием замкнутого резонатора, состоящего из трех и более отражателей, возбудителя двух встречнобегущих электромагнитных волн с одинаковыми частотами (ƒ₁ и ƒ₂ соответственно) и детектора, фиксирующий одинаковое время прохождения встречных волн по замкнутому контуру при отсутствии угловой скорости и разность времени прохождения встречных волн при наличии угловой скорости.

Информация о действующей угловой скорости Ω выделяется по разности частот Δƒ=ƒ₁-ƒ₂ встречных волн, величина которой может быть найдена из следующего выражения:

где S - площадь замкнутого резонатора, L - периметр замкнутого резонатора, λ - средняя длина волны, определяемая как

λ≈4πс/(ƒ₁+ƒ₂).

Оно представляет собой лазерный гироскоп, состоящего из катода, двух анодов, трех зеркал, призмы и приемника.

С помощью катода и двух анодов происходит возбуждение двух встречно бегущих электромагнитных волн с одинаковыми частотами ƒ₁ и ƒ₂ соответственно (ƒ₁=ƒ₂). Через полупрозрачное зеркало обе волны поступают на приемник, где измеряется сдвиг фаз, пропорциональный угловой скорости Ω.

При отсутствии вращения (Ω=0) встречнобегущие волны имеют одинаковую частоту (ƒ₁=ƒ₂), а также нулевой сдвиг по фазе между ними.

При вращении замкнутого резонатора частота одной из волн увеличивается, а другой уменьшается. При этом встречнобегущие волны приобретают дополнительные фазовые сдвиги ϕ₁=arctgξ₁ и ϕ₂=arctgξ₂, где ξ_{1, 2}=±QΔƒ/ƒ - обобщенная расстройка частот волн из-за наличия вращения, Q - добротность резонатора.

Величина дифференциального фазового сдвига, приобретаемого встречнобегущими волнами, составляет ϕ₁-ϕ₂=2arctg(QΔƒ/ƒ), или, принимая при малых угловых скоростях QΔƒ/ƒ<<1 и используя выражение (1), окончательно получаем

,

где с - скорость света.

Недостатком такого способа является невозможность измерения сверхмалых угловых скоростей из-за малого периметра замкнутого резонатора (порядка 30-40 см).

Наиболее близким по технической сущности к данному изобретению является способ измерения сверхмалых угловых скоростей, основанный на разном времени прохождения встречных электромагнитных волн по замкнутому резонатору при наличии угловой скорости [Schreiber U., Igel Н., Cochard A., Velikoseltsev A., Flaws A., Schuberth В., Drewitz W., The GEOsensor project: rotations - a new observable for seismology // Observation of the Earth System from Space. - Springer Berlin Heidelberg, 2006. - C. 427-443; Великосельцев A.A., Лукьянов Д.П., Виноградов В.И., Шрайбер К.У. Современное состояние и перспективы развития сверхбольших оптических гироскопов для применения в геодезии и сейсмологии. Квантовая электроника. 2014. Т. 44. №12. С. 1151-1156], заключающийся в размещении на поверхности Земли замкнутого резонатора с периметром 16 метров, состоящего из четырех отражателей, возбудителя двух встречнобегущих электромагнитных волн с одинаковыми частотами (ƒ₁ и ƒ₂ соответственно) и приемника, детектирующего одинаковое время прохождения встречных волн по резонатору при отсутствии угловой скорости и разность времени прохождения встречных волн при наличии угловой скорости.

Значение фазового сдвига в данном методе зависит от размеров резонатора и пропорционально скорости вращения. Следовательно, при условии, что длина пути электромагнитной волны внутри резонатора точно известна, измерение фазового сдвига дает точное значение скорости вращения датчика. Этот фазовый сдвиг пересчитывается в разность частот двух встречных электромагнитных волн в тех случаях, когда волны распространяются по активной среде замкнутого резонатора [G.Е. Stedman. Ring-laser tests of fundamental physics and geophysics. Rep.Prog. Phys. 60, 615. 1997]. Можно записать, что разность частот двух волн

где n - нормаль к плоскости распространения электромагнитных волн; Ω - угловая скорость вращения; K - масштабный коэффициент, определяемый площадью S и периметром L резонатора и оптической длиной волны λ.

Поскольку наблюдаемая частота биений двух электромагнитных волн пропорциональна скорости вращения, коэффициент S определяет разрешение измеряемой величины.

Возможность построения резонаторов с большим периметром становится более сложным и практически невозможным. Это обуславливается принципиальным ограничением возможного размера периметра замкнутого резонатора, вызванного с одной стороны сближением продольных типов колебаний встречнобегущих волн, а с другой прецизионными точностями изготовления отдельных элементов замкнутого резонатора.

Таким образом, недостатком известного способа является недостаточная точность измерений сверхмалых угловых скоростей из-за малого периметра резонатора.

Задачей, решаемой изобретением, является повышение точности измерений сверхмалых угловых скоростей за счет увеличения периметра замкнутого резонатора.

Для решения поставленной задачи в предлагаемом способе, также как и в известном, измерение сверхмалых угловых скоростей осуществляется путем возбуждения двух встречно-бегущих электромагнитных волн, отражения, детектирования их параметров и расчета величины действующей угловой скорости, пропорциональной изменению этих параметров. Но в отличие от известного возбудитель, отражатели и детектор установлены на не менее трех геостационарных спутниках и возбуждают электромагнитные волны. Это становится возможным из-за распространения электромагнитных волн в свободном пространстве, при этом практически они не испытывают помех от внешних возмущений.

Достигаемый технический результат - повышение точности измерений сверхмалых угловых скоростей.

Совокупность признаков, сформулируемых в п. 2, характеризует способ измерения сверхмалых угловых скоростей, в котором детектируют разность фаз электромагнитных волн и рассчитывают угловую скорость по формуле

,

где S - площадь контура, λ, с - длина волны и скорость распространения встречных электромагнитных волн соответственно, Ω - детектируемая угловая скорость.

Совокупность признаков, сформулируемых в п. 3, характеризует способ измерения сверхмалых угловых скоростей, в котором детектируют разность времен прохождения двумя электромагнитными волнами периметра резонатора и рассчитывают по формуле

где L₁ и L₂ - расстояние, которое проходят две встречно-бегущие в резонаторе электромагнитные волны, с - длина волны и скорость распространения встречных электромагнитных волн соответственно, Ω - детектируемая угловая скорость.

Применение способов по п. 2 и по 3 дает близкую точность и выбор какого-то одного из них будет определяться оборудованием, установленным на спутниках.

Предлагаемый способ поясняется чертежами, где:

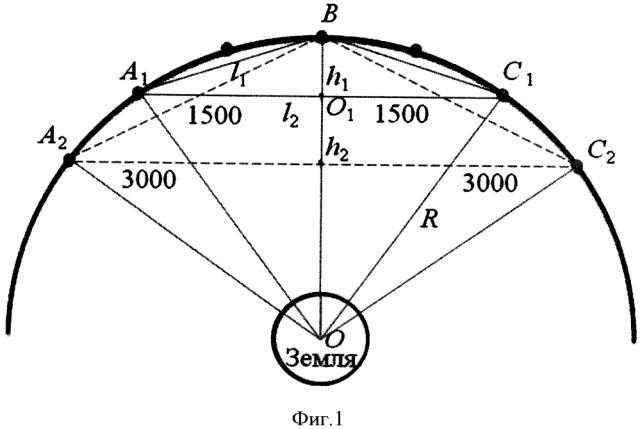
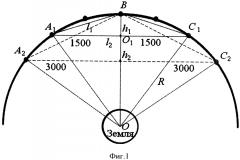
на фиг. 1 - приведена общая схема устройства, реализующего предлагаемый способ измерения сверхмалой угловой скорости.

Рассмотрим устройство, реализующее предлагаемый способ (фиг. 1). Оно состоит из трех или более спутников, расположенных на геостационарной орбите Земли с радиусом R=42164 км. На них размещается открытый замкнутый резонатор, состоящий из трех и более отражателей, двунаправленного возбудителя двух встречнобегущих электромагнитных волн с одинаковыми частотами (ƒ₁ и ƒ₂ соответственно) и приемника (фазового детектора), детектирующего одинаковый набег фаз встречных волн по замкнутому контуру при отсутствии угловой скорости и разность набега фаз ϕ₁ и ϕ₂ встречных волн при наличии угловой скорости в форме

,

где S - площадь контура, λ, с - длина волны и скорость распространения встречных электромагнитных волн соответственно.

Рассмотрим два простейших варианта замкнутого резонатора А₁ВС₁ и А₂ВС₂ (фиг. 1), образованного тремя спутниками (на фиг. 1 они обозначены А₁, В, С₁ и А₂, В, С₂ соответственно) и имеющего форму равностороннего треугольника (в общем случае форма замкнутого резонатора может быть различной). Если обозначить через - расстояние между спутниками А₁ и В, которое равно расстоянию между спутниками В и С₁ (т.е. резонатор - равносторонний треугольник), а - расстояние между спутником А₁ и точкой O₁ пересечения линии, соединяющей спутники A₁ и С₁, с высотой замкнутого резонатора h₁, имеющего треугольную форму. Периметр резонатора А₁ВС₁ будет определяться по формуле

,

а его площадь

.

Значение высоты первого замкнутого резонатора h₁ можно найти из выражения для прямоугольного треугольника O₁ОС₁ (фиг. 1)

,

где R - радиус геостационарной орбиты относительно центра Земли.

Откуда . Получим классическое квадратное уравнение

.

Решая его найдем значение h₁

D=(-2*42146)²-4*1500²=7105141264-9000000=7096141264 (км)

, .

, .

Так как h₁₁=84318,5 км больше диаметра геостационарной орбиты (чего не может быть), то h₁=26.5 км.

Тогда площадь резонатора А₁ВС₁ (км²).

Для определения периметра необходимо найти значение , которое определяется из следующего выражения

.

Откуда км.

Тогда периметр резонатора А₁ВС₁ L₁=2⋅1500.23+2⋅1500=6000.46 (км), а его масштабный коэффициент составит

.

Для прототипа S_п=16 м², L_п=16 м и, следовательно, .

Таким образом, в предлагаемом способе, по сравнению с прототипом, масштабный коэффициент, а следовательно и чувствительность, увеличится в 6.6 раза. И это не предел. Рассмотрим теперь резонатор в форме треугольника А₂ВС₂.

Масштабный коэффициент для способа по п. 2 составит

.

Для сравнения, как показано в работе [Д.П. Лукьянов, В.Я. Распопов, Ю.В. Филатов. Прикладная теория гироскопов. СПб.: ГНЦ РФ ОАО "Концерн "ЦНИИ "Электроприбор", 2015. - 316 с.] K_1ϕ для волоконно-оптического гироскопа со средней чувствительностью (а значит, и средней точностью) составляет , а для высокоточного (высокоточного) - . При этом точность измерений также зависит от выбранной дины волны: чем она больше, тем меньше точность.

Аналогично можно определить высоту второго треугольного резонатора А₂ВС₂ h₁₂=107 км, а также его площадь S₂=321000 (км²) и периметр L₂=12003.82 км. Следовательно, масштабный коэффициент для резонатора А₂ВС₂ составит , а увеличение чувствительности в 26.7 раза.

Таким образом, описание предлагаемого способа свидетельствуют о том, что с помощью предлагаемого способа достигается технический результат - увеличение точности измерения сверхмалых угловых скоростей.

1. Способ измерения сверхмалых угловых скоростей путем возбуждения встречно-бегущих электромагнитных волн, отражения, детектирования их параметров и расчета величины действующей угловой скорости, пропорциональной изменению этих параметров, отличающийся тем, что возбудитель, отражатели и детектор установлены на не менее трех геостационарных спутниках и возбуждают электромагнитные волны.

2. Способ по п. 1, отличающийся тем, что детектируют разность фаз электромагнитных волн и рассчитывают угловую скорость по формуле

где S - площадь контура, λ, с - длина волны и скорость распространения встречных электромагнитных волн соответственно, Ω - детектируемая угловая скорость.

3. Способ по п. 1, отличающийся тем, что детектируют разность времен прохождения двумя электромагнитными волнами периметра резонатора и рассчитывают по формуле

где L₁ и L₂ - расстояние, которое проходят две встречно-бегущие в резонаторе электромагнитные волны, с - длина волны и скорость распространения встречных электромагнитных волн соответственно, Ω - детектируемая угловая скорость.