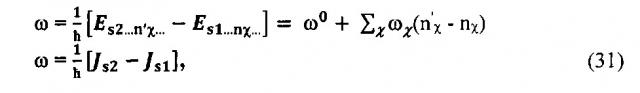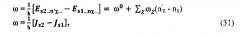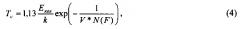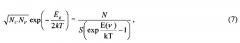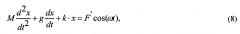Способ эффективного осуществления гиперпроводимости и сверхтеплопроводности

Способ эффективного осуществления гиперпроводимости и сверхтеплопроводности

Иллюстрации

Показать все

Реферат

Область техники, к которой относится изобретение

Изобретение относится к электричеству, к электрофизике и теплопроводности материалов, к явлению нулевого электрического сопротивления, то есть к гиперпроводимости, а также к явлению нулевого теплового сопротивления, то есть к сверхтеплопроводности материалов при околокомнатных и более высоких температурах.

Гиперпроводимость представляет собой состояние материала с нулевым электрическим сопротивлением. Такое состояние, состояние гиперпроводимости или гиперпроводящее состояние возникает и существует в содержащих электронно-колебательные центры (ЭКЦ) полупроводниковых материалах между электродами при температурах гиперпроводящего перехода (Т_h) и при более высоких температурах [1-16]. Материалы, в которых наблюдается гиперпроводимость и сверхтеплопроводность при их нагревании выше температуры T_h, являются гиперпроводниками или гиперпроводящими материалами.

Сверхтеплопроводность представляет собой состояние материала с нулевым тепловым сопротивлением. Такое состояние, состояние сверхтеплопроводности или сверхтеплопроводное состояние возникает и существует в содержащих ЭКЦ полупроводниковых материалах между электродами при температуре гиперпроводящего перехода Т_h и при более высоких температурах.

Электронно-колебательными центрами или ЭКЦ являются такие локальные центры, равновесные положения или частоты упругих колебаний которых зависят от их электронного состояния в материалах [17-20]. В работе [20] "О влиянии деформации решеток электронами на оптические и электрические свойства кристаллов" на стр. 207 в параграфе 3 приведено определение электронно-колебательных переходов локального центра:

"3. Фотопереходы электронов¹⁰

В этом параграфе будут рассмотрены фотопереходы слабо связанных электронов локального "центра" с дискретного на дискретный энергетический уровень. Рассмотрим переход из состояния s₁…n_χ… в состояние . При этом переходе изменяются не только квантовые числа электронов s, но и квантовые числа колебаний n_χ т.е. выделяется теплота. Частота света, поглощаемого при таком переходе, равна

где ω₀ - частота, поглощаемая "чисто электронным переходом", при котором .

Вероятность фотоперехода вычисляется при помощи обычного квантовомеханического рассмотрения¹⁰.

Энергию света, поглощаемого упомянутым электронно-колебательным переходом за секунду в единице объема диэлектрика, можно записать в виде…"

В данной выдержке из указанной работы С.И. Пекара дано определение электронно-колебательных переходов локальных центров. Локальные центры, в которых происходят электронно-колебательные переходы, т.е. центры электронно-колебательной природы называют электронно-колебательными центрами или ЭКЦ.

Электронные или дырочные переходы на энергетические уровни ЭКЦ или с этих уровней сопряжены с неизбежным участием значительного числа квантов упругих колебаний материала из-за чего их называют электронно-колебательными переходами. Среднее число участвующих в таких переходах фононов численно равно константе электрон-фононной связи Пекара-Хуана-Риса (S). Константа электрон-фононного взаимодействия на ЭКЦ обычно значительно превышает 1 и по теоретическим данным может достигать 150. Известны экспериментальные значения S=22 в широкозонном материале, в диэлектрике. В типичных полупроводниках величина S обычно составляет несколько единиц. Так, в кремнии на А-центрах, представляющих собой ассоциации примесных атомов кислорода с вакансиями, константа S близка к 5, хотя при отсутствии ЭКЦ в материале S≤0,25. Известно, что упругое взаимодействие ЭКЦ друг с другом вызывает уменьшение S. Благодаря участию фононов в электронно-колебательных переходах и их взаимодействию с движениями атомных ядер в материалах открыты принципиально новые, считавшиеся ранее невозможными технические эффекты, такие как колебания атомных ядер в атомах материалов, СВЧ излучение при электронно-колебательных переходах, увлечение электронов фононами при дебаевых температурах фононов, а также гиперпроводимость и сверхтеплопроводность.

Гиперпроводимость и сверхтеплопроводность практически осуществлены в широкозонных материалах и в узкозонных материалах. Примесные атомы кислорода в материалах практически важны для осуществления гиперпроводимости и сверхтеплопроводности поскольку кислород содержится в коре Земли (28%) и присутствует в полупроводниковых материалах. Так в промышленном кремнии концентрация примесных атомов кислорода может быть близка к 10¹⁸ см^-3 и не поддается существенному уменьшению при современных способах очистки. Часть примесных атомов кислорода в материале переводят в состав ЭКЦ без легирования материала другими примесями для создания ЭКЦ. Используют такие ЭКЦ для осуществления гиперпроводимости и сверхтеплопроводности.

Гиперпроводимость и сверхтеплопроводность являются взаимно связанными состояниями материалов и не могут быть осуществлены порознь, отдельно друг от друга. Это обусловлено тем, что при наличии в материале электронно-колебательных центров электроны и фонононы оказываются сильно связанными друг с другом на электронно-колебательных энергетических уровнях ЭКЦ. В таких условиях электроны и фононы совместно осуществляют переходы, которые получили название электронно-колебательных переходов. Среди таких переходов есть электронно-колебательные переходы с энергетических уровней одного ЭКЦ на энергетические уровни другого ЭКЦ, например, при наличии градиента концентрации ЭКЦ или градиента электрического потенциала, электрического поля или градиента температуры. Такие электронно-колебательные переходы являются квантовыми переходами, они сопровождаются пространственным переносом в материале электрических зарядов электронов и дырок, а также пространственным переносом связанных с электронами и дырками фононов и собственных (Inherent, I-) колебаний атомных ядер в атомах материала, чем обусловлено возникновение и существование гиперпроводимости и сверхтеплопроводности.

Собственные (Inherent, I-) колебания представляют собой упругие периодические колебательные смещения атомных ядер относительно электронных оболочек атомов или ионов материала, то есть I-колебания являются колебательными движениями атомных ядер в потенциальных полях электронных оболочек атомов или ионов материала.

Известны также волны I-колебаний, представляющие собой пространственное распространение I-колебаний в материале, из-за которых кинетические эффекты в материалах приобретают важные особенности.

Электроны, дырки, фононы, I-колебания взаимно связаны друг с другом на ЭКЦ посредством сильного электрон-фононного взаимодействия. При этом система атомных ядер обменивается энергией с системой электронов в материале. Такой энергетический обмен в материалах противоречит адиабатическому приближению Борна-Оппенгеймера [21] которое лежит в основе доминирующей сейчас адиабатической электроники материалов.

Действительно, теоретической основой современной твердотельной электроники является квантовое уравнение Шредингера для кристалла, включающее операторы кинетической энергии электронов (Т_е), кинетической энергии атомных ядер (T_z), операторы потенциальных энергий кулоновского расталкивания электронов (V_ee), кулоновского расталкивания ядер (V_zz) и кулоновского притяжения электронов к ядрам (V_ez):

где W - полная энергия кристалла. Решением этого уравнения является волновая функция Ψ(ℜ, r), зависящая от совокупности координат атомных ядер (ℜ) и от совокупности координат электронов (r). Известно, что точное решение уравнения (1) затруднено по принципиальным и техническим причинам.

В 1926 году М. Борн и П. Оппенгеймер предложили приближенный метод решения уравнения (1) положив Ψ(ℜ, r)=ϕ(r, ℜ)⋅Ф(ℜ) и представили его в виде двух следующих уравнений:

где кристаллический потенциал V_кр=V_кp(ℜ, r)=V_ee+V_zz+V_ze; ϕ(r, ℜ) - волновая функция, описывающая движение системы электронов; Е - полная энергия системы электронов; Ф(ℜ) - волновая функция, описывающая движение системы атомных ядер, Е - энергия системы электронов,

- адиабатический потенциал, j - номер атома в материале, Ω - объем материала. По существу, величина потенциала A определяется зависимостью электронной волновой функции ϕ(r, ℜ) от смещений атомных ядер. М. Борн и П. Оппенгеймер [21] исключили потенциал А из уравнения (3) считая его вклад в энергию материала несущественным. Этот приближенный метод решения уравнения (1) с помощью уравнений (2) и (3) при условии A≡0 получил название адиабатического приближения Борна-Оппенгеймера, поскольку при таком условии, систему электронов представляли отделенной от системы ядер адиабатической оболочкой, препятствующей обмену энергией между этими системами. Полагали, что в этом приближении обмен энергией между электронами и ядрами атомов в материалах невозможен. Очевидно, что адиабатическое приближение, адиабатический принцип Борна-Оппенгеймера является приближенным способом решения уравнения Шредингера для материала и, как выяснилось, применение адиабатического приближения Борна-Оппенгеймера ограничивает круг доступных для исследования и использования физических процессов в материалах.

В 1930 году нобелевский лауреат, один из основателей волновой квантовой механики и создателей ее математического аппарата П. Дирак впервые показал, что адиабатическое приближение Борна-Оппенгеймера в общем случае обосновать нельзя [22]. Тем не менее, приближение Борна-Оппенгеймера получило широкое распространение и сейчас оно лежит в основе электронной теории материалов, в основе доминирующей современной электроники. В связи с этим существующую сейчас в науке и технике твердотельную, в том числе, полупроводниковую электронику, можно обоснованно называть адиабатической электроникой, электроникой Борна-Оппенгеймера. Эта электроника в силу ее приближенного характера не дает исчерпывающего ответа на многие вопросы о природе материалов и о физических явлениях в них, например, таких как сверхпроводимость, сверхтекучесть, гиперпроводимость, сверхтеплопроводность, увлечение электронов фононами при температурах Дебая фононов отчасти в силу ограниченности адиабатического приближения Борна-Оппенгеймера. Дальнейшие исследования упрочили понимание ограниченности адиабатического приближения при его использовании в решении проблем материалов вообще и проблем твердотельной электроники в частности.

Установлено, что даже в адиабатическом приближении Борна-Оппенгеймера, когда потенциал А≡0 и поэтому обмен энергией между ярами и электронами локальных центров якобы отсутствует, тем не менее, такой энергетический обмен все же происходит. Обмен энергией между системой электронов и системой атомных ядер в материалах происходит постоянно, поскольку кристаллический потенциал V_кp в уравнении (2) зависит и от совокупности координат ядер (ℜ) и от совокупности координат электронов (r) из-за чего решения уравнений (2, 3) и их собственные значения, вообще говоря, зависят от совокупностей координат ℜ и r. Таким образом, адиабатическое приближение Борна-Оппенгеймера оказалось адиабатическим только условно, приближенно. Реальность такова, что обмен энергией между системой электронов и системой атомных ядер является принципиальным и неотъемлемым свойством материалов: молекул, жидкостей, твердых тел. Однако, колебания ядер в атомах материалов, их взаимодействие с электронами и фононами почти не изучали с самого основания квантовой науки о материалах, т.е. последние сто лет. В связи с этими данными следует отметить, что утвердившиеся в физике представления о куперовских парах и теория сверхпроводимости Бардина-Купера-Шриффера (БКШ) используют обмен энергией между электронами, используют обмен электронов фононами, представляющими собой упругие колебания атомов кристаллической решетки, колебания атомов или ионов материала. Иначе говоря, теория куперовских пар и связанная с ней теория сверхпроводимости БКШ в принципе используют обмен энергией между системой электронов и системой атомов (ионов) в материале. Это соответствует адиабатическому приближению Борна-Оппенгеймера, поскольку атомы и ионы в этих теориях рассматриваются как материальные точки. В этом приближении не предполагаются ни самостоятельные смещения атомных ядер, ни обмен энергиями между электронами и ядрами, не смотря на то, что движения атомных ядер и движения электронов представлены в уравнении Шредингера для материала (1) отдельными, независимыми друг от друга операторами кинетических энергий.

Заявленное изобретение относится к новой развивающейся неадиабатической электронике. В отличие от существующей традиционной и доминирующей сейчас адиабатической электроники Борна-Оппенгеймера неадиабатическая электроника усиливает с помощью ЭКЦ обмен энергией между атомными ядрами, фононами и электронами в материалах и использует такой энергетический обмен для научных и технических применений.

Таким образом, неадиабатическая электроника представляет собой новое научно-техническое направление, основанное на неотвратимом, но не учитывавшимся ранее обмене энергией между электронами и ядрами атомов в молекулах, газах, жидкостях, в конденсированных материалах и материальных структурах. Особенно интенсивно и ярко эффекты неадиабатической электроники проявляются в полупроводниковых материалах и структурах в виде собственных (I-, Inherent) α-, β- и γ-типов колебаний ядер внутри атомов материалов; в виде глубоких электронно-колебательных уровней в запрещенной энергетической зоне полупроводников (и диэлектриков); в процессах генерирования, усиления, детектирования и преобразования частот СВЧ колебаний и волн на ЭКЦ; в виде увлечения электронов фононами при дебаевых температурах фононов; в виде явлений гиперпроводимости и сверхтеплопроводности, а также в виде отрицательного электрического сопротивления; в явлении электрического управления тепловыми потоками; в оптических, электрических и магнитных способах регулирования оптических свойств материалов; в возможности создавать неохлаждаемые низкошумящие твердотельные электронные и отоэлектронные приборы и устройства.

Открытие I-колебаний и волн в материалах увеличило количество физически важных степеней свободы для частиц, образующих материал; увеличило количество каналов обмена энергией, т.е. взаимодействий между частицами материала. Новые взаимодействия проявляются в виде принципиально новых технических эффектов и в виде новых особенностей известных эффектов.

При определенных условиях в ограниченных областях материала I-колебания и волны становятся когерентными, то есть приобретают одинаковые частоты и фазы колебаний. Такие области материала с одинаковыми фазами упругих колебаний получили название когерентных областей. Когерентность упругих колебаний является условием нулевого электрического сопротивления и нулевого теплового сопротивления материала в когерентных областях, то есть условием гиперпроводимости и сверхтеплопроводности когерентных областей материала является именно когерентность I-колебаний и связанных с ними фононов. Геометрические размеры когерентных областей могут иметь размеры от десятков ангстрем до десятков и сотен микрон при различных технических условиях. Если когерентная область занимает весь материал на протяжении между электродами, то электрическое и тепловое сопротивления материала между электродами становятся нулевыми, тем самым реализуются гиперпроводимость и сверхтеплопроводность материала между электродами.

Переход материала в гиперпроводящее состояние происходит при его нагревании до температуры гиперпроводящего перехода T_h или до более высоких температур и представляет собой явление гиперпроводимости, технический эффект гиперпроводимости. Состоянию гиперпроводимости материала сопутствует состояние сверхтеплопроводности. Явление перехода материала в состояние с нулевым тепловым сопротивлением, в состояние сверхтеплопроводности представляет собой технический эффект сверхтеплопроводности. Явления, эффекты гиперпроводимости и сверхтеплопроводности возникают вблизи температуры гиперпроводящего перехода Т_h и существуют при более высоких температурах. Гиперпроводимость и сверхтеплопроводность являются взаимно связанными техническими эффектами, они не могут быть отделены друг от друга, возникают и существуют совместно, могут быть осуществлены и практически использованы при температурах выше Т_h.

Данное изобретение обеспечивает увеличение эффективности известного способа осуществления гиперпроводимости и сверхтеплопроводности [16]. В заявленном способе реализован технический механизм формирования нулевого электрического сопротивления и нулевого теплового сопротивления материалов между электродами, то есть гиперпроводимости и сверхтеплопроводности при околокомнатных и более высоких температурах за счет использования электронно-колебательных центров и характерного для ЭКЦ сильного электрон-фононного взаимодействия в условиях вывода из материала избыточной колебательной энергии.

Изобретение может быть использовано в наноэлектронике, микроэлектронике, радиотехнике, электротехнике и радиоэлектронике.

Уровень техники

Переход материалов в состояние с нулевым электрическим сопротивлением при низких температурах известен как открытое в 1911 году явление сверхпроводимости [23]. На фиг. 1 приведена типичная температурная зависимость электрического сопротивления (R) сверхпроводникового материала. Из фиг. 1 видно, что его электрическое сопротивление R обращается в ноль при охлаждении материала ниже температуры сверхпроводящего перехода (Т_с). Сверхпроводимость наблюдается только у некоторых материалов и только при известных условиях, а именно, если температура материала ниже температуры сверхпроводящего перехода, а плотность электрического тока и напряженность магнитного поля в материале ниже критических значений J_к и Н_к [24-26]. Наличие критических значений T_c, J_к и Н_к ограничивает технические применения сверхпроводимости вблизи комнатных и при более высоких температурах, поскольку значения J_к и Н_к зависят от температуры материала и стремятся к нулю при повышении и приближении температуры к T_c.

Первые сверхпроводники имели малые значения T_c: 4,1 К (ртуть), 7,3 K (свинец). В 1967 г. была обнаружена сверхпроводимость в сплаве соединений ниобия, алюминия и германия с T_c≅20К. В 1986 г. Ж.Г. Беднорцем и К.А.З. Мюллером был обнаружен класс металлооксидов с T_c≅40К [27] в связи с чем им была присуждена Нобелевская премия. Позже было открыто много классов высокотемпературных сверхпроводников, а максимальная температура сверхпроводящего перехода достигла 133К-134К. В соединении HgBa₂Ca₂Cu₃O₈ под давлением в десятки Гигапаскалей обнаружен сверхпроводящий переход при температурах от 156К до 164К. Обнаружена сверхпроводимость при температурах около 200К в соединении SrRuO₃ подвергнутом лазерной обработке [28]. Полученный в работе [29] материал (Sn₅In)Ba₄Ca₂Cu₁₀O_Y, демонстрирует сверхпроводимость при температурах до T_c=212K, предположительно до T_c=250K.

Нужно отметить, что сверхпроводимость во всех классах сверхпроводящих материалов была обнаружена экспериментально, без теоретического прогноза, практически "вслепую", а доминирующие представления о сверхпроводимости нередко основываются на неподходящем для этих целей адиабатическом приближении Борна-Оппенгеймера. Экспериментальные поиски сверхпроводящих материалов с высокими значениями T_c все еще продолжаются. Эта важная задача более ста лет решается путем подбора химического состава и технологических обработок материалов, то есть по-прежнему "поиском вслепую", напоминающим средневековую алхимию, новых сверхпроводящих материалов с высокими значениями T_c. Считается определенным и несомненным, что при температуре меньше T_c сверхпроводниковый материал может быть сверхпроводящим, может обладать нулевым электрическим сопротивлением. Ожидания сверхпроводимости именно при температуре Т<Т_с традиционно основаны на имеющихся эмпирических данных. Известные физические модели явления сверхпроводимости также ориентированы на существование сверхпроводящего состояния материала при температуре меньше T_c.

Полноценной теории сверхпроводников пока не создано, но выдвинуто несколько физических механизмов, призванных объяснить явление сверхпроводимости. Среди этих механизмов доминирующее положение занимает фононный механизм, объясняющий попарное притяжение электронов проводимости из-за обмена электронов друг с другом виртуальными кристаллическими фононами, сопровождающееся образованием "электронных пар", так называемых «пар Купера» или «куперовских электронных пар». Энергия связи электронов в "электронной паре" определяет величину T_c. Данный механизм лежит в основе общеизвестной теории сверхпроводимости Ж. Бардина, Н. Купера, Ж. Шриффера (БКШ) [30], в которой температура сверхпроводящего перехода T_c зависит от энергии связанного с электронами упругого колебания материала (Е_кол):

где k - постоянная Больцмана, V* - энергия связи упругого колебания материала с электроном, N(F) - плотность электронных состояний при энергии Ферми, F - энергия Ферми. Например, в сверхпроводящих металлах V*N(F)<<1, Е_кол≤17 мэВ и поэтому T_c не превышает 20К. Казалось, что теория БКШ не объяснила наблюдаемые на опыте высокие экспериментальные значения T_c. Это давало повод полагать, что данная теория верна только для низкотемпературных сверхпроводников.

Однако, основываясь на теории БКШ [30] в работах [31, 32] была сформулирована принципиальная возможность увеличения температуры сверхпроводящего перехода (Т_с) за счет использования фононов с большими энергиями. Эти работы в принципе объясняют высокие значения T_c практически наблюдаемые при осуществлении технических эффектов гиперпроводимости и сверхтеплопроводности, в которых используются I-колебания ядер в атомах материалов, содержащих электронно-колебательные центры (ЭКЦ) кванты упругих колебаний которых многократно превышают энергии оптических и акустических фононов. Именно поэтому гиперпроводимость и сверхтеплопроводность осуществляются в содержащих ЭКЦ материалах.

Для увеличения T_c ранее предлагали использовать в куперовских парах более энергичные фононы, с большими энергиями, с волновыми векторами, пронизывающими несколько зон Бриллюэна (Ларкин А.И.). Однако данное предложение технически не было реализовано.

Б.Д. Джозефсон открыл два технических эффекта [33] подтвержденные экспериментально, отмеченные Нобелевскими премиями и проявляющиеся в структурах, состоящих из двух сверхпроводников, разделенных туннельно тонким диэлектрическим слоем, а именно: стационарный эффект Джозефсона и нестационарный высокочастотный эффект Джозефсона.

Стационарный эффект Джозефсона проявляется в виде постоянного электрического тока (I₀), протекающего сквозь туннельно тонкий слой диэлектрика, разделяющего сверхпроводники, даже если между сверхпроводниками не приложено электрическое напряжение. Этот ток объяснили туннелированием куперовских пар электронов сквозь диэлектрик. Величина и направление туннельного тока сквозь диэлектрический слой толщиной порядка десятка ангстрем зависит от разности фаз колебаний куперовских пар в сверхпроводниках. На фиг. 2 приведена вольтамперная характеристика джозефсоновского туннельного контакта двух одинаковых сверхпроводников из работы [24]. Из фиг. 2 видно, что при нулевом напряжении между сверхпроводниками сквозь диэлектрический слой течет постоянный ток I₀, представляющий стационарный эффект Джозефсона.

Нестационарный высокочастотный эффект Джозефсона проявляется в виде переменного электрического тока, протекающего сквозь туннельно тонкий слой диэлектрика, разделяющего сверхпроводники, если между сверхпроводниками приложено постоянное электрическое напряжение величиной V. Циклическая частота этого переменного тока

где е - заряд электрона. Квант энергии таких колебаний . Частота ω/2π обычно соответствует СВЧ диапазону.

В сверхпроводниках действует эффект Мейснера [24] состоящий в том, что материал в сверхпроводящем состоянии, в состоянии с нулевым электрическим сопротивлением, выталкивает из своего объема внешнее магнитное поле. При этом возникают и действуют значительные механические силы, расталкивающие материал и магнит. Эффект Мейснера практически используется в устройствах магнитной подвески, в которых сверхпроводниковые материалы охлаждают до температур ниже T_c, что технически неудобно и затратно.

В невырожденных и слабо вырожденных полупроводниках и полупроводниковых содержащих ЭКЦ структурах, то есть в гиперпроводниках, спонтанно возникают и существуют области когерентности с характерным размером Λ (с длиной когерентности Λ) от десятков ангстрем до десятков микрон, которые обладают нулевым электрическим (и нулевым тепловым) сопротивлением. Благодаря нулевому сопротивлению когерентных областей гиперпроводники и гиперпроводниковые структуры выталкивают из своего объема внешнее магнитное поле, проявляя действие эффекта Мейснера. То есть эффект Мейснера является характерным и для сверхпроводников, и для гиперпроводников вследствие нулевого электрического сопротивления существующих в них когерентных областей.

Эффект Мейснера в гиперпроводниках проявляется практически при температурах спонтанного формирования когерентных областей и усиливается при увеличении объема когерентных областей в материале, например, при увеличении температуры материала. Эффект Мейснера проявляется в материале между электродами при температурах ниже температуры гиперпроводящего перехода Т_h, при температуре Т_h и выше Т_h. Таким образом, технический эффект Мейснера и его технические приложения вполне осуществимы с помощью гиперпроводников при низких, околокомнатных и более высоких температурах. Для усиления эффекта Мейснера в гиперпроводниках целесообразно увеличивать суммарный объем когерентных областей, например, увеличивая их количество, характерный размер, т.е. длину когерентности Λ, например, используя технические средства, предложенные в заявленном изобретении.

Эффект Мейснера проявляется в виде силы, выталкивающей материал с нулевым электрическим сопротивлением из магнитного поля, т.е. эффект Мейснера характеризуют вектором силы: модулем вектора, представляющим величину эффекта, и направлением вектора силы. Изменение эффекта Мейснера состоит из изменения величины (модуля) силы и из изменения направления этой силы.

До 2000 года осуществление нулевого электрического сопротивления материала при околокомнатных и более высоких температурах представляла нерешенную научно-техническую проблему. Более того, не была доказана сама возможность осуществления сверхпроводимости при комнатной температуре и тем более, выше комнатной температуры. Не было доказано и отсутствие такой возможности. Теперь установлено, что в определенных условиях в полупроводниковых материалах между электродами возникает состояние с нулевым электрическим сопротивлением при околокомнатных и более высоких температурах, получившее название гиперпроводимости, сопровождающееся возникновением нулевого теплового сопротивления материала, получившего название сверхтеплопроводности.

Экспериментальное осуществление гиперпроводимости и сверхтеплопроводности стало возможным в результате открытия и исследования нового типа упругих колебаний и волн в материалах, Inherent, I-колебаний и волн [1, 4, 7-15, 34-38]. I-колебания и волны представляют собой упругие колебания ядер в атомах материалов. Оказалось, что I-колебания и волны эффективно взаимодействуют с электронами, дырками, и фононами обеспечивая тем самым сильное электрон-фононное взаимодействие, сильную электрон-фононную связь, благодаря которой возникает гиперпроводимость и сверхтеплопроводность. Были определены α-, β- и γ-типы I-колебаний и волн, вычислены элементарные кванты таких колебаний (E_Z) в атомах материалов в зависимости от атомного номера (Z), различными экспериментальными методами измерены кванты таких колебаний в ряде атомов. На фиг. 3 светлыми кружками указаны вычисленные энергии элементарных квантов этих типов I-колебаний в атомах с атомными номерами Z от 1 до 80, а темными кружками указаны соответствующие значения квантов, измеренные различными экспериментальными методами. Из фиг. 3 видно, что наибольшие величины квантов таких колебаний и волн соответствуют колебаниям α-типа, при которых ядро атома осциллирует относительно его электронной оболочки в окрестности ее центра, вблизи равновесного положения ядра в атоме, совпадающего с положением минимума потенциала, создаваемого электронами оболочки атома. Величина квантов I-колебаний α-типа монотонно уменьшается от 0,519 эВ до 0,22 эВ при увеличении Z от 1 до 8 и затем монотонно увеличивается до 0,402 эВ при дальнейшем увеличении Z до 80 и более. Такие кванты I-колебаний взаимодействуя с электронами и дырками согласно формуле (4) способны обеспечить нулевое электрическое и нулевое тепловое сопротивления материалов, гиперпроводящее состояние, при температурах от Т_h до 2500 K и выше, то есть температура сверхпроводящего перехода T_c в данном случае может превышать 2500 K. Иначе говоря, сверхпроводимость, сверхпроводящее состояние в принципе может существовать в материалах до температуры их плавления и вероятно в расплавах материалов, когда в расплаве обеспечивается достаточная связь электронов с I-колебаниями атомных ядер.

I-колебания атомного ядра в атоме определенного сорта характеризуются вполне определенной величиной элементарного кванта таких колебаний и набором колебательных термов существенно отличающихся от энергии квантов I-колебаний и набора колебательных термов атомов другого сорта. Экспериментальное определение квантов I-колебаний атомных ядер в газообразных, жидких и твердотельных материалах позволяет надежно идентифицировать такие атомы по величине и набору колебательных термов, что может быть положено в основу действия приборов, определяющих атомный состав материалов.

I-колебания проявляют незначительную ангармоничность. Профиль сферически симметричного потенциального поля в окрестности центра электронной оболочки, в котором движется ядро атома, отличается от параболической зависимости, из-за чего возникают ангармонические поправки к энергии гармонических колебаний. Поправки для одномерных колебаний α-типа (ΔE_αν) с колебательными числами ν=0, 1, 2 и 3 вычислены в первом и втором порядках стационарной теории возмущений согласно [39, стр. 93]. Как и следовало ожидать, наибольшие значения поправок относятся к колебательным состояниям с ν=3, соответствующим наибольшим смещениям ядер из равновесных положений в центрах электронных оболочек. На фиг. 4 графически представлены поправки к энергии I-колебаний α-типа в состояниях с ν=0, 1, 2, 3 для атомов в зависимости от атомного номера Z. На вставке фиг. 4 поправки представлены в другом масштабе для атомов с Z>10. Представленные на фиг. 4 данные выявили незначительную ангармоничность I-колебаний.

Согласно имеющимся экспериментальным данным I-колебания являются одномерными, их колебательные энергии описываются формулой линейного гармонического квантового осциллятора:

где E_Z - элементарный квант колебаний, а колебательное квантовое число ν принимает значения 0, 1, 2, 3, …

В экспериментах проявляются электронно-колебательные переходы с колебательных уровней ЭКЦ в минимум осцилляторного потенциала с полной потерей энергии I-колебаний. Возможны электронно-колебательные переходы даже с потерей энергии так называемых «нулевых колебаний», равной E_Z/2. Это не соответствует свободному квантовому гармоническому осциллятору, для которого согласно квантовой теории состояние в минимуме параболического потенциала в центре электронной оболочки недопустимо. Однако для классического осциллятора такое состояние разрешено. В этом состоит дуализм свойств ЭКЦ, проявляющих квантовые и классические свойства. Иначе говоря, ЭКЦ, I-колебания не являются свободными (идеальными) и обмениваются энергией (кристаллических фононов различных типов) с окружающей средой. Учитывая это, следует полагать, что осцилляторы, описывающие I-колебания ЭКЦ, являются линейными, одномерными гармоническими осцилляторами, проявляющими и квантовые и классические свойства, а стационарные колебательные энергии I-колебаний атомных ядер в ЭКЦ описываются формулой (6), включая еще энергию Е_кол=0, соответствующую минимуму осцилляторного потенциала.

Величина Е_кол в полупроводниках может превышать ширину запрещенной зоны материала, если значение ν достаточно велико. Соответствующая температура сверхпроводящего перехода T_c, согласно (4) может превышать десятки тысяч градусов. Такие температуры, несомненно, относятся не к материалу в целом, а только к участвующим в I-колебаниях локальным центрам.

Описываемые формулой (6) электронно-колебательные энергетические уровни ЭКЦ проявляются в полупроводниках в виде так называемых глубоких энергетических уровней, преимущественно лежащих в запрещенной зоне полупроводника. Согласно данным о рекомбинации электронов и дырок на ЭКЦ, об энергиях активации сопротивления содержащих ЭКЦ материалов, большинство из электронно-колебательных уровней ЭКЦ действительно лежат в запрещенной зоне полупроводника, как показано на фиг. 5. В центре фиг. 5 изображена энергетическая схема полупроводника, где Е_с и E_v обозначают энергии дна зоны проводимости и потолка валентной зоны, F - уровень Ферми. Рассматриваемые электронно-колебательные центры расположены в объеме полупроводника, в точках с координатами r₀ и . Параболические потенциалы, удерживающие атомное ядро вблизи центра электронной оболочки ЭКЦ, представлены слева и справа на фиг. 5 параболами V(r-r₀) и . Энергетические уровни ЭКЦ с различными значениями колебательного квантового числа ν=0, 1, 2, … показаны пунктирными горизонтальными линиями. Электронные переходы из зоны проводимости на колебательные уровни ЭКЦ с ν>0 показаны вертикальными направленными вниз от Е_с стрелками. Переходы дырок на колебательные уровни ЭКЦ изображены вертикальными направленными вверх от E_v стрелками. Для этого ветви параболы V(r-r₀) обращены вниз, а ветви параболы обращены вверх, как показано на фиг. 5. Именно такие положения потенциальных кривых V(r-r₀) и соответствуют возбуждению I-колебаний ЭКЦ за счет энергии электронных или дырочных переходов. Эти переходы преимущественно происходят с испусканием или поглощением нескольких кристаллических фононов, возбуждают I-колебания атомных ядер в атомах ЭКЦ и поэтому они являются электронно-колебательными переходами. Электронно-колебательный процесс на ЭКЦ можно представить