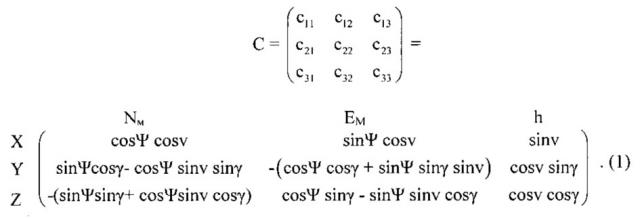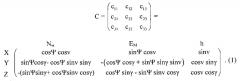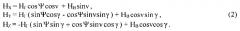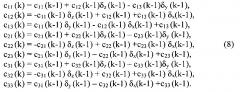Способ измерения магнитного курса подвижного объекта

Способ измерения магнитного курса подвижного объекта

Иллюстрации

Показать все

Реферат

Способ измерения магнитного курса подвижного объекта относится к способам автономной навигации объектов с использованием нескольких датчиков без применения внешних источников информации, в частности глобальных навигационных систем.

Известен способ измерения магнитного курса подвижного объекта [1], заключающийся в использовании трех магнитометров и трех акселерометров, жестко закрепленных на подвижном объекте, оси которых параллельны связанным осям подвижного объекта. Способ предполагает наличие априорной информации о вертикальной или горизонтальной составляющей вектора магнитного поля Земли (МПЗ).

Недостатком способа [1] является низкая точность. Главной причиной этого является то, что, несмотря на принципиальную возможность априорной оценки той или иной составляющей МПЗ по широте, долготе и высоте объекта, на практике эта оценка может быть выполнена достаточно грубо. Это обусловлено погрешностями существующих пространственных моделей МПЗ, естественными вариациями поля во времени, а также аномалиями и возмущениями различного происхождения. Кроме того, имеет место неопределенность в определении знака квадратного корня при использовании величины v в выражении (2) [1]. К низкой точности также приводит отсутствие измерений составляющих угловой скорости, что особенно важно при высокой динамике движения объекта вокруг центра масс (динамичных углах тангажа и крена).

Наиболее близким к заявляемому способу является способ [2] измерения магнитного курса подвижного объекта по показаниям трех магнитометров, трех акселерометров и не менее двух датчиков угловой скорости, жестко закрепленных на подвижном объекте, оси которых параллельны связанным осям подвижного объекта.

Недостатком способа [2] является его низкая точность. Главными причинами являются, во-первых, предположение, как и в способе [1], об априори известной вертикальной составляющей МПЗ и, во-вторых, (что более существенно), необходимость априорного знания значения вертикальной составляющей линейного ускорения подвижного объекта. Последнее на практике в принципе невозможно, поскольку эта составляющая может быть определена по данным акселерометров только при известных направляющих косинусах связанных осей объекта относительно местной вертикали, но именно в нахождении этих косинусов и состоит суть решаемой задачи.

Принципиальным отличием заявляемого способа от прототипа является отсутствие необходимости априорного знания указанных вертикальных составляющих.

Техническим результатом использования заявляемого способа является повышение точности измерения магнитного курса подвижного объекта

Для получения указанного технического результата в способе измерения магнитного курса подвижного объекта по показаниям трех магнитометров, трех акселерометров и двух датчиков угловой скорости, жестко закрепленных на подвижном объекте, оси которых параллельны связанным осям подвижного объекта, считают известным ускорение силы тяжести, по данным акселерометров определяют режим движения объекта: равномерный или с ускорением, в обоих режимах определяют направляющие косинусы связанных осей объекта относительно местной вертикали, по значениям которых вычисляют углы его тангажа и крена, а используя значения этих углов и данные магнитометров, определяют магнитный курс, при этом в режиме равномерного движения указанные направляющие косинусы определяют непосредственно по данным акселерометров, в режиме с ускорением - по данным трех датчиков угловой скорости путем пошаговой коррекции матрицы направляющих косинусов связанных осей объекта относительно направлений на магнитные север и восток и местной вертикали на интервалах, в течение каждого из которых проекции вектора угловой скорости объекта могут считаться постоянными, при переходе объекта в режим движения с ускорением в качестве начального условия коррекции используют значение матрицы направляющих косинусов, вычисленное по углам магнитного курса, тангажа и крена на момент окончания режима равномерного движения.

Существенные отличия заявляемого способа по сравнению с прототипом.

1. Считают известным ускорение силы тяжести. Это предположение имеет достаточно серьезные основания [3], поскольку ускорение силы тяжести известно с высокой точностью.

В прототипе ускорение силы тяжести не учитывается и не используется. Вместо этого используются другие, указанные выше, исходные данные, получить которые с требуемой точностью не представляется возможным.

2. По данным акселерометров определяют режим движения объекта: равномерный или с ускорением. Определение режима движения объекта позволяет при нахождении направляющих косинусов использовать специфические точные алгоритмы измерения магнитного курса для каждого из режимов. При равномерном движении вычисление магнитного курса подвижного объекта осуществляется аналитически с использованием достаточно простых соотношений, а при движении с ускорением - численными методами, которые гарантируют получение результата с наперед заданной точностью. Причем результаты измерений, полученные в предыдущем режиме (интервале), используются в качестве начальных условий для последующего.

В прототипе режим движения объекта не анализируется, но делается попытка сразу решить нелинейную систему уравнений для движения объекта с ускорением, что приводит к большим вычислительным затратам и неоднозначному решению.

3. В обоих режимах движения объекта определяют направляющие косинусы связанных осей объекта относительно местной вертикали, по значениям которых вычисляют углы тангажа и крена.

В прототипе углы тангажа и крена (и магнитного курса) вычисляют, решая нелинейную систему уравнений с непредсказуемыми результатами.

4. Используя значения углов тангажа и крена, а также данные магнитометров, определяют магнитный курс, при этом в режиме равномерного движения указанные направляющие косинусы определяют аналитически непосредственно по данным акселерометров.

В прототипе применяют общий алгоритм оценки углов для движения с ускорением с плохими результатами.

5. В режиме с ускорением указанные направляющие косинусы определяют по данным трех датчиков угловой скорости путем пошаговой коррекции матрицы направляющих косинусов связанных осей объекта относительно направлений на магнитные север и восток и местной вертикали на интервалах.

В прототипе вся матрица направляющих косинусов не рассматривается.

6. Выбор интервалов коррекции матрицы направляющих косинусов, исходя из условия, что в течение каждого из них проекции вектора угловой скорости объекта могут считаться постоянными. Такой подход позволяет корректировать матрицу направляющих косинусов с заранее заданной точностью.

В прототипе дискретный режим работы и коррекция матрицы не рассматриваются.

7. При переходе объекта в режим движения с ускорением в качестве начального условия коррекции используют значение матрицы направляющих косинусов, вычисленное по углам магнитного курса, тангажа и крена на момент окончания режима равномерного движения.

В прототипе режимы движения объекта не рассматриваются.

Предлагаемый способ можно пояснить следующим образом.

Используются две системы координат.

а) Магнитная географическая система координат (СК) ON_ME_Mh с началом в центре масс подвижного объекта. Оси ON_M, OE_M лежат в плоскости местного горизонта, ось ON_M направлена на магнитный север (полюс), ось OE_M - на магнитный восток. Ось Oh совпадает с местной вертикалью и направлена вверх.

Данная система координат непосредственно связана с векторами индукции магнитного поля и ускорения силы тяжести Земли. А именно, северная ось ON_M совпадает по направлению с горизонтальной составляющей Н_Г магнитного поля, ось Oh - с его вертикальной составляющей Н_В. Проекция поля на восточную ось OE_M равна нулю. Аналогично, вертикальная составляющая вектора ускорения силы тяжести равна его модулю g, две другие проекции равны нулю.

б) Связанная СК OXYZ с тем же началом. Оси OX, OY совпадают с продольной и поперечной строительными осями объекта. Ось OZ перпендикулярна этим осям (вертикальная ось). При нулевых углах тангажа v и крена γ объекта оси OX, OY лежат в плоскости местного горизонта, ось OZ перпендикулярна этой плоскости и направлена вверх. Ось ОХ совпадает с направлением движения объекта. Ориентация оси ОХ относительно оси ON_M определяет магнитный курс подвижного объекта Ψ. Оси чувствительности соосных магнитометров, акселерометров и датчиков угловой скорости совпадают с осями СК OXYZ.

Такой выбор систем координат характерен для пешеходных навигационных систем. Для подвижных объектов других типов возможно другое задание связанной СК. В принципиальном плане приводимые далее результаты это не меняет,

В общем случае при произвольных углах Ψ,v, γ взаимная ориентация систем координат определяется матрицей направляющих косинусов вида:

Из (1) видно, что составляющие магнитного поля Н_Г, Н_В связаны с измерениями проекций H_X, H_Y, H_Z поля на оси чувствительности магнитометров соотношениями:

Разрешая систему уравнений (2) при измеренных значениях H_X, H_Y, H_Z и известных углах тангажа v и крена γ относительно неизвестного магнитного курса Ψ, приходим к выражению:

Для заданного состава измерительных датчиков (магнитометры, акселерометры, датчики угловой скорости) возможны два варианта высокоточного определения углов v, γ, соответствующих режимам равномерного движения объекта и движения с ускорением.

При равномерном движении объекта (заметим, что неподвижный объект является частным случаем равномерного движения с нулевой линейной скоростью) применяется вариант, основанный на использовании акселерометров. В этом случае проекции а_х, a_y, a_z вектора ускорения силы тяжести, фиксируемые осями чувствительности акселерометров, равны:

(здесь учтено, что вектор ускорения силы тяжести направлен вертикально вниз, т.е. со знаком «минус»). По показаниям акселерометров (4) рассчитываются направляющие косинусы

по значениям которых вычисляются углы тангажа и крена:

Подставив (6) в (3), получают искомый угол магнитного курса Ψ.

В режиме равномерного движения при любой угловой ориентации объекта (любых углах v, γ) показания акселерометров а_х, a_y, a_z определяются только величиной ускорения силы тяжести g, т.е. справедливо равенство:

которое на практике выполняется с некоторым допуском ±Δ, зависящим от точности используемых акселерометров. При движении с ускорением показания а_х, a_y, a_z содержат дополнительные составляющие, вызванные собственным неизвестным линейным ускорением объекта. В результате равенство (7) нарушается, а соотношения (4), (5) становятся несправедливыми. В этом случае переходят ко второму варианту определения направляющих косинусов с₁₃, с₂₃, с₃₃, по значениям которых в соответствии с выражениями (6) продолжают вычисление углов тангажа и крена.

Подчеркнем, что проверка выполнения (невыполнения) равенства (7) служит правилом определения режима движения объекта.

Для режима движения с ускорением воспользуемся методом пошагового расчета (коррекции) матрицы направляющих косинусов С (соотношение (1)) по данным датчиков угловых скоростей ω_х, ω_y, ω_z [4]. В соответствии с этим методом коррекция элементов матрицы с₁₁, с₁₂, …, с₃₃ на интервалах времени (шагах) Т=t_k-t_k-1, в течение которых проекции ω_x,, ω_y, ω_z могут считаться постоянными, проводится по рекуррентному алгоритму:

Здесь δ_x=ω_xT, δ_y=ω_yT, δ_z=ω_zT - парциальные (пошаговые) приращения углов, k - номер очередного интервала (шага). Алгоритм (8) является скалярной формой записи общего метода [4] для малых по сравнению с постоянными времени процессов ω_х, ω_y и ω_z интервалов Т.

Соотношения (8) легко реализуются на современных вычислительных средствах. Последовательно выполняя алгоритм (8), получают пошаговые значения направляющих косинусов с₁₃, с₂₃, c₃₃, необходимые для вычислений по формулам (6), (3). При этом начальное значение матрицы С=С(0) соответствует моменту окончания режима равномерного движения (равенство (7) нарушается) и рассчитывается по формуле (1) по значениям углов магнитного курса, тангажа и крена на указанный момент времени. При возвращении к режиму равномерного движения (равенство (7) восстанавливается) также возвращается прежний порядок вычислений по формулам (5), (6), (3), и так далее.

Заявляемый способ иллюстрируют следующие графические материалы:

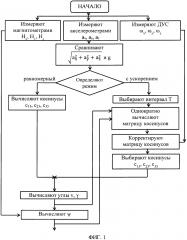
Фиг. 1 - алгоритм работы заявляемого способа.

Применение заявляемого способа заключается в реализации алгоритма, изображенного на Фиг. 1.

Перед проведением измерений трехосные магнитометр, акселерометр и датчики угловой скорости должны пройти калибровку, аналогичную [5] и [6], которая должна позволить:

1. Устранить различия в чувствительностях по осям X, Y и Z соответствующего прибора путем определения соответствующих поправочных коэффициентов.

2. Устранить методическую ошибку измерений путем определения соответствующих поправочных констант.

Эти действия не указаны в формуле изобретения, как, впрочем, и в аналогах, хотя без такой калибровки ни один из указанных способов работать не может.

Рассмотрим реализацию заявляемого способа по алгоритму (см. Фиг. 1).

Акселерометрами измеряют проекции а_х, a_y, a_z вектора ускорения силы тяжести, магнитометрами измеряют проекции Н_х, H_y, H_z вектора магнитного поля, а датчиками угловой скорости - проекции ω_х, ω_y, ω_z вектора угловой скорости объекта. Проверяют соотношение (7), в результате чего определяют характер движения объекта: равномерный или с ускорением.

При равномерном характере движения вычисляют направляющие косинусы с₁₃, c₂₃, c₃₃, используя соотношения (5).

Если анализ соотношения (7) показывает, что объект движется с ускорением, то, используя данные о возможной динамике объекта и(или) данные ДУС, выбирают интервал Т, в течение которого угловая скорость объекта может считаться постоянной.

При переходе режима движения объекта от равномерного к движению с ускорением по полученным ранее углам тангажа v, крена γ и магнитного курса Ψ вычисляют начальное значение матрицы направляющих косинусов С(0), используя соотношение (1), и далее пошагово с интервалом Т корректируют матрицу направляющих косинусов (1), используя значения матрицы направляющих косинусов, полученные на предыдущем интервале, и данные ДУС, по соотношениям (8).

При любом характере движения объекта по полученным направляющим косинусам c₁₃, c₂₃, c₃₃, аналитически, используя соотношения (6), вычисляют углы тангажа v и крена γ. По этим углам, используя соотношение (3), вычисляют искомый магнитный курс объекта Ψ.

Рассмотрим возможность технической реализации заявляемого способа измерения магнитного курса подвижного объекта.

Современные навигационные системы реализуются по единой схеме: совокупность измерителей, в данном случае трехосных акселерометров, магнитометров и датчиков угловой скорости, подключаются к компьютеру, который обычно (из-за необходимости вычисления прямых и обратных тригонометрических функций) реализуется в виде цифрового процессора обработки сигналов. Результаты обработки входной информации - тангажа v, крена γ и магнитного курса Ψ поступают потребителю. Естественно, что все такие системы работают в дискретном времени, что согласуется с пошаговым способом коррекции матрицы направляющих косинусов в режиме движения объекта с ускорением.

Таким образом, заявляемый способ измерения магнитного курса подвижного объекта может быть реализован и обеспечивает повышение его точности.

Источники информации

1. Патент RU 2130588. «Способ измерения магнитного курса подвижного объекта». – Опубл. 20.05.1999.

2. Патент RU 2262075. «Способ измерения магнитного курса подвижного объекта и устройство для его осуществления». – Опубл. 10.10.2005. Бюл. №28.

3. Статья «Ускорение свободного падения». / [Электронный ресурс]. - Режим доступа: http://ru.wikipedia.org/wiki/Ускорение_свободного_падения.

4. Кузовков Н.Т., Салычев О.С. Инерциальная навигация и оптимальная фильтрация. - М: Машиностроение, 1982, 216 с.

5. Патент RU 2572109. «Способ калибровки электронного магнитного компаса». – Опубл. 27.12.2015. Бюл. №36.

6. Патент RU 2577806. «Способ калибровки акселерометрического трехосевого инклинометра». – Опубл. 20.03.2016. Бюл. №8.

Способ измерения магнитного курса подвижного объекта по показаниям трех магнитометров, трех акселерометров и двух датчиков угловой скорости, жестко закрепленных на подвижном объекте, оси которых параллельны связанным осям подвижного объекта, отличающийся тем, что, считая известным ускорение силы тяжести, по данным акселерометров определяют режим движения объекта: равномерный или с ускорением, в обоих режимах определяют направляющие косинусы связанных осей объекта относительно местной вертикали, по значениям которых вычисляют углы его тангажа и крена, а используя значения этих углов и данные магнитометров, определяют магнитный курс, при этом в режиме равномерного движения указанные направляющие косинусы определяют непосредственно по данным акселерометров, в режиме с ускорением - по данным трех датчиков угловой скорости путем пошаговой коррекции матрицы направляющих косинусов связанных осей объекта относительно направлений на магнитные север и восток и местной вертикали на интервалах, в течение каждого из которых проекции вектора угловой скорости объекта могут считаться постоянными, при переходе объекта в режим движения с ускорением в качестве начального условия коррекции используют значение матрицы направляющих косинусов, вычисленное по углам магнитного курса, тангажа и крена на момент окончания режима равномерного движения.