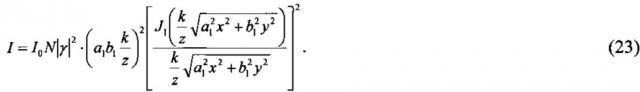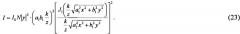Способ измерения характеристик деформируемости эритроцитов (варианты)

Способ измерения характеристик деформируемости эритроцитов (варианты)

Иллюстрации

Показать все

Реферат

Область техники

Группа изобретений относится к устройствам медицинской диагностической техники, предназначенным для измерения деформируемости красных клеток крови.

Уровень техники

Измерения деформируемости эритроцитов важны для диагностики и лечения многих заболеваний, в том числе таких распространенных как нарушения мозгового кровообращения, артериальная гипертония и сахарный диабет. Для измерений используется метод лазерной дифрактометрии эритроцитов в сдвиговом потоке (эктацитометрия). Этот метод основан на получении и анализе дифракционных картин, возникающих при рассеянии лазерного пучка на суспензии эритроцитов, деформированных в сдвиговом потоке силами вязкого трения.

Актуальной проблемой медицинской диагностики является проблема измерения деформируемости эритроцитов. Деформируемость определяется как мера способности клеток крови изменять свою форму под действием внешних сил. Этот параметр существенно влияет на микроциркуляцию крови в органах и тканях человеческого организма, а потому имеет прямое отношение к диагностике и лечению многих заболеваний. Известно, что деформируемость эритроцитов понижена при таких заболеваниях, как серповидно-клеточная анемия, наследственный сфероцитоз, талассемия, острое нарушение мозгового кровообращения, диабет. Измерение деформируемости эритроцитов важно и в связи с проблемой хранения крови для переливаний.

В настоящее время известно несколько способов измерения деформируемости эритроцитов [Dobbe J.G.G., Hardeman M.R., Streekstra G.J., Starckee J., Ince C., Grimbergen C.A., Analyzing red blood cell-deformability distributions, Blood Cells, Molecules, and Diseases, 28 (3), p. 373 (2002) - далее (1)]. Это втягивание эритроцитов в микропипетку, растягивание эритроцитов лазерным пинцетом, видеосъемка эритроцитов, деформированных в сдвиговом потоке силами вязкого трения. Однако эти методы являются весьма сложными и трудоемкими. Кроме того, они требуют большого времени для измерений и обработки данных. Более простым методом является пропускание пробы крови под давлением через пористый фильтр. Однако этот метод требует значительного количества крови и не всегда дает надежные результаты.

Одним из наиболее удобных методов измерения деформируемости эритроцитов является лазерная дифрактометрия эритроцитов в сдвиговом потоке (эктацитометрия) [Bessis М., Mohandas N., A diffractometric method for the measurement of cellular deformability, Blood Cells, 1, pp. 307-313 (1975) - далее (2)]. Этот метод основан на наблюдении и анализе дифракционных картин, возникающих при рассеянии лазерного пучка на суспензии эритроцитов, деформированных в сдвиговом протоке силами вязкого трения. Существуют приборы для таких измерений. Это лазерные эктацитометры ЛОРКА (Голландия) Реоскан (Корея), ЛАДЭ (Реомедлаб, Россия). Однако пока эти приборы недоступны для широкой клинической практики. Актуальна проблема стандартизации этих приборов, повышения надежности и точности измерений.

Еще один важный аспект проблемы заключается в том, что в крови любого человека разные эритроциты обладают разной способностью к деформации. С этой точки зрения деформируемость следует рассматривать как статистическую характеристику ансамбля эритроцитов и использовать для ее описания такие понятия как среднее значение, дисперсия, функция распределения и т.п. В принципе, эти параметры можно измерять методом прямого наблюдения за эритроцитами в сдвиговом потоке [1]. Однако этот метод труден в реализации.

В нескольких работах ставилась задача измерения статистических характеристик деформируемости эритроцитов методом лазерной эктацитометрии. В работе [Plasek J., Marik Т., Determination of undeformable erythrocytes in blood samples using laser light scattering, Applied Optics, 21 (23), p. 4335 (1982)] предложено определять долю слабодеформируемых эритроцитов в образце крови, измеряя интенсивность света в некоторой точке дифракционной картины (ДК) как функцию сдвигового напряжения. В работе [Rasia R.J., Schutz G., A numerical method to determine erythrocyte deformability distribution using data from Fraunhofer light diffraction, Clinical Hemorheology, 13, pp. 641-649 (1993)] обсуждается возможность измерения среднего значения и дисперсии деформируемости эритроцитов в предположении о том, что эритроциты имеют гауссово распределение по деформируемости. В работе [Streekstra G.J., Dobbe J.G.G., Hoekstra A.G., Quantification of the poorly deformable red blood cells using ektacytometry, Optics Express, 18 (13), p. 14173 (2010)] показано, что путем анализа ДК для бимодального ансамбля эритроцитов можно измерить долю слабо деформируемых эритроцитов, если при данном сдвиговом напряжении известны дифракционные картины для обеих компонент ансамбля. В работе [Rabai М., Meiselman H.J., Wenby R.B., Detterich J.A., Feinberg J., Analysis of light scattering by red blood cells in ektacytometry using global pattern fitting, Biorheology, 49, pp. 317-328 (2012)] предложена многопараметрическая модель, позволяющая промоделировать рассеяние лазерного пучка бимодальным по деформируемости ансамблем эритроцитов при произвольном сдвиговом напряжении.

В работах [Nikitin S. Yu., Priezzhev A.V., Lugovtsov A. E., Analysis of laser beam scattering by an ensemble of particles modeling red blood cells in ektacytometer, Journal of Quantitative Spectroscopy and Radiative Transfer, 121, pp. 1-8 (2013), далее (3)] проведено теоретическое моделирование рассеяния лазерного излучения клетками крови и на этой основе разработаны новые алгоритмы обработки данных. Предложены два таких алгоритма: алгоритм характеристической точки и алгоритм кривизны линии изоинтенсивности. Эти алгоритмы проверены экспериментально на специально подготовленных образцах крови крыс. Эти результаты относятся к периферической части дифракционной картины, лежащей вблизи первого минимума интенсивности рассеянного света. В этой области интенсивность рассеянного света I примерно на порядок меньше интенсивности центрального дифракционного максимума I(0). В работе [Никитин С.Ю., Юрчук Ю.С., Упрощенный алгоритм измерения дисперсии деформируемости эритроцитов на основе метода лазерной эктацитометрии. Квантовая Электроника, 45 (8), стр. 776-780 (2015) далее (4)] была рассмотрена центральная часть дифракционной картины, определяемая условием 0.4≤I/I(0)≤0.6. В этой работе получено уравнение, связывающее между собой дисперсию деформируемости эритроцитов и геометрические параметры дифракционной картины. Достоинством этого уравнения является то, что оно не содержит энергетических параметров. Это существенно упрощает процедуру измерений. Однако анализ, проведенный в работе [4], ограничен случаем ансамбля эритроцитов с симметричным распределением по деформируемости.

Как уже отмечалось выше, одним из наиболее удобных методов измерения деформируемости эритроцитов является лазерная дифрактометрия эритроцитов в сдвиговом потоке (эктацитометрия). Существуют разные типы эктацитометров. Общим для этих приборов является то, что деформация эритроцитов осуществляется силами вязкого трения, а информация о форме частиц извлекается из дифракционной картины, возникающей при рассеянии лазерного пучка на суспензии эритроцитов.

В ротационном эктацитометре сильно разбавленную суспензию эритроцитов заливают в зазор между стенками двух прозрачных коаксиальных стаканов, один из которых неподвижен, а другой может вращаться со ступенчато изменяемой угловой скоростью (так называемая ячейка Куэтта). Вращение подвижного стакана вызывает течение жидкости и появление в ней сдвиговых напряжений, которые ориентируют эритроциты определенным образом и вытягивают их в направлении потока. Для наблюдения за изменением формы частиц суспензию просвечивают лазерным пучком. Пучок рассеивается на эритроцитах и дает на экране наблюдения дифракционную картину, которая содержит в себе информацию о форме исследуемых частиц. При малых скоростях вращения подвижного стакана центральное дифракционное пятно имеет круглую форму, а при больших скоростях оно становится близким к эллиптическому, что свидетельствует о выстраивании эритроцитов в сдвиговом потоке и вытягивании их в направлении потока под действием сил вязкого трения. Схема лазерного эктацитометра эритроцитов показана на Фиг. 1, где 1 - лазер, 2 - ячейка Куэтта, 3 - зеркало, 4 - двигатель, 5 - видеокамера, 6 - персональный компьютер, 7 - линза.

Дифракционную картину снимают на видеокамеру и в цифровом виде передают в компьютер, где она обрабатывается по определенному алгоритму. Обычная процедура обработки данных состоит в следующем. Компьютер выбирает на экране наблюдения точки, в которых интенсивность рассеянного света имеет некоторое определенное значение. Эти точки образуют линию, называемую линией изоинтенсивности. Как правило, эту линию выбирают на периферии центрального дифракционного максимума. Затем линию изоинтенсивности аппроксимируют эллипсом. Измеряют большую (L) и малую (S) полуоси эллипса и вычисляют параметр DI=(L-S)/(L+S), называемый параметром (индексом) деформируемости (DI - Deformability Index) эритроцитов. Такие измерения повторяют при нескольких скоростях вращения подвижного стакана. В результате получают зависимость параметра деформируемости эритроцитов от сдвигового напряжения - так называемую функцию деформируемости или кривую деформируемости эритроцитов. Эта кривая выглядит по-разному для разных образцов крови. В частности, у пациентов с острым нарушением мозгового кровообращения деформируемость эритроцитов заметно ниже, чем у здоровых людей такого же возраста. В этом и в других случаях лазерная эктацитометрия эритроцитов позволяет выявить реологическое нарушение, оценить его степень и подобрать адекватное лечение. Подобные анализы необходимы при серповидно-клеточной анемии, наследственном сфероцитозе и малярии. В последние годы появляется все больше свидетельств того, что контроль деформируемости эритроцитов необходим при лечении таких социально значимых заболеваний как ишемия, артериальная гипертония и сахарный диабет. Достоинствами лазерной эктацитометрии по сравнению с другими методами измерения деформируемости эритроцитов являются простота, быстрота измерений и обработки данных, возможность получения данных сразу для больших ансамблей частиц при использовании минимальных количеств крови (2-3 микролитра).

Лазерная эктацитометрия эритроцитов была предложена в 1975 году Бессис и Мохандас [2], и с тех пор используется без существенных изменений, позволяя измерять лишь среднюю деформируемость эритроцитов в исследуемом образце крови. Однако в крови здорового, а тем более больного человека, разные эритроциты имеют разную способность к деформации. Это дает основание рассматривать деформируемость как статистическую характеристику ансамбля эритроцитов и использовать для ее описания такие понятия как функция распределения, среднее значение, дисперсия и т.п.

Раскрытие изобретения

Задачей настоящего изобретения является разработка нового способа измерения средней деформируемости эритроцитов, дисперсии (ширины) деформируемости эритроцитов и коэффициента асимметрии распределения эритроцитов по деформируемости, используя принцип лазерной эктацитометрии.

Техническим результатом является возможность измерять новые параметры - среднюю деформируемость эритроцитов, дисперсию деформируемости эритроцитов и коэффициент асимметрии распределения эритроцитов по деформируемости без необходимости измерения энергетических параметров линии изоинтенсивности дифракционной картины; получение более точного рецепта измерения основной измеряемой величины, а именно, средней деформируемости эритроцитов в исследуемом образце крови. Таким образом, данный способ позволит более точно определять уровень интенсивности рассеянного света на линии изоинтенсивности, выбранной для измерений, что существенно упростит процедуру измерений.

Технический результат достигается тем, что способ измерения характеристик деформируемости эритроцитов включает видеозапись и обработку дифракционной картины, возникающей при рассеянии лазерного пучка на разбавленной суспензии эритроцитов, деформированных в сдвиговом потоке силами вязкого трения, оцифровке этой дифракционной картины, определении формы линии изоинтенсивности, лежащей в области дифракционной картины, где интенсивность рассеянного света примерно вдвое меньше интенсивности центрального дифракционного максимума, измерении координат полярных точек линии изоинтенсивности x_p и y_p, лежащих на пересечении данной линии изоинтенсивности с горизонтальной осью координат и с вертикальной осью координат, а также радиусов кривизны R(x_p) и R(y_p) данной линии изоинтенсивности в указанных полярных точках с последующим вычислением средней деформируемости эритроцитов s, дисперсии (ширины) деформируемости эритроцитов μ и коэффициента асимметрии распределения эритроцитов по деформируемости ν по математическим формулам.

Краткое описание чертежей

Изобретение поясняется чертежами, где:

на фиг. 1 - изображена схема лазерного эктацитометра эритроцитов;

на фиг. 2 - изображен пример линии изоинтенсивности (а), полярные точки и круги кривизны линии изоинтенсивности в полярных точках (б);

на фиг. 3 - изображены распределения интенсивности рассеянного света вдоль горизонтальной (А) и вертикальной (В) осей координат в дифракционной картине, построенной по формулам (17), (25), (26);

на фиг. 4 - изображено численное моделирование дифракционных картин для унимодального (А), асимметричного бимодального (В) и симметричного бимодального (С) ансамблей эритроцитов; соответствующие линии изоинтенсивности (D, Е, F); и круги кривизны линий изоинтенсивности в полярных точках (G, Н, I);

на фиг. 5 - изображены дифракционные картины для унимодального (А), асимметричного бимодального (В), и симметричного бимодального (С) ансамблей эритроцитов; соответствующие им линии изоинтенсивности (D, Е, F); построение кругов кривизны линий изоинтенсивности в полярных точках (G, Н, I). Все дифракционные картины получены при одном и том же сдвиговом напряжении;

на фиг. 6 - изображены распределения интенсивности света в дифракционной картине, показанной на фиг. 5а, вдоль горизонтальной (а) и вертикальной (b) осей координат;

на фиг. 7 - изображены исходная (а) и сглаженная (b) линии изоинтенсивности для унимодального ансамбля эритроцитов.

Осуществление изобретения

В настоящем изобретении предлагается способ измерения характеристик деформируемости эритроцитов, применимый для образцов крови с произвольным распределением эритроцитов по деформируемости.

В способе использована обработка данных лазерной эктацитометрии эритроцитов. Работоспособность способа проверена методом численного моделирования, а также в экспериментах с образцами человеческой крови. Особенностью способа является необходимость измерения только геометрических параметров дифракционной картины, в то время как ее энергетические параметры измерять не обязательно. Это значительно упрощает процедуру измерений.

Эритроциты в сдвиговом потоке моделируются как плоские эллиптические диски [3]. В отличие от модели эритроцитов как эллипсоидов, модель плоских дисков дает возможность в аналитической форме найти связь между параметрами ДК и характеристиками ансамбля эритроцитов. Основанием для предлагаемого способа измерения эритроцитов является изображение эритроцитов в сдвиговом потоке, полученное с помощью микроскопа [3]. Кроме того, как показано в работе [3], модель плоских дисков дает достаточно высокую точность в области малых углов рассеяния, используемой в лазерной эктацитометрии эритроцитов.

Исходя из того, что полуоси дисков a и b считаются случайными величинами, они определяются формулами:

Здесь а₀ и b₀ - средние размеры полуосей, ε - случайный параметр формы. Такая модель позволяет описать ансамбль эритроцитов с учетом того, что разные клетки обладают разной способностью к деформации. Будем считать, что и .

Условие (2) соответствует слабой неоднородности ансамбля эритроцитов по деформируемости. Это условие, как правило, хорошо выполняется для реальных образцов крови. Характеристиками ансамбля эритроцитов в предлагаемом изобретении являются средняя деформируемость эритроцитов s, дисперсия деформируемости μ и коэффициент асимметрии распределения эритроцитов по деформируемости v. Эти величины определяются формулами:

Параметры μ и ν характеризуют дисперсию деформируемости эритроцитов и коэффициент асимметрии распределения эритроцитов по деформируемости. Как видно из формул (1), (3), они имеют смысл второго и третьего моментов отклонения максимального (и минимального) размера полуосей эритроцитов в сдвиговом потоке лазерного эктацитометра от их средних значений. Эти величины подлежат определению на основе анализа ДК, возникающих при рассеянии лазерного пучка на суспензии эритроцитов в эктацитометре.

Введем декартовы координаты на плоскости экрана наблюдения. Ось x направим по горизонтали, ось y - по вертикали. Физически направления этих осей выделены тем, что одна из них параллельна потоку жидкости в эктацитометре, а другая - перпендикулярна этому потоку. Начало координат выберем в центре ДК, т.е. в точке падения на экран прямого лазерного пучка. Анализ ДК проводят, используя понятие линии изоинтенсивности (ЛИ). Т.е. линия на экране наблюдения, на которой интенсивность рассеянного света I имеет некоторое постоянное значение. Назовем полярными точками ЛИ точки пересечения этой линии с декартовыми осями координат.Всего таких точек 4, однако, в силу симметрии ЛИ достаточно рассмотреть только 2 из них, например, правую полярную точку и верхнюю полярную точку. С помощью лазерного эктацитометра можно измерить параметры

Здесь х_р - координата полярной точки, лежащей на пересечении данной ЛИ с горизонтальной осью координат [мм], y_р - координата полярной точки, лежащей на пересечении данной линии изоинтенсивности (ЛИ) с вертикальной осью координат [мм], R(x_p) - радиус кривизны данной ЛИ в первой из указанных полярных точек [мм], R(y_p) - радиус кривизны данной линии изоинтенсивности во второй из указанных полярных точек [мм]; D, C₁, С₂ - числовые безразмерные параметры ЛИ. Параметр D характеризует вытянутость ЛИ, величины C₁ и С₂ характеризуют кривизну ЛИ в полярных точках.

Пример линии изоинтенсивности, полярные точки этой линии, а также круги кривизны линии изоинтенсивности, построенные в полярных точках, показаны на Фиг. 2. На основе проведенного анализа была установлена связь характеристик ансамбля эритроцитов (3) с параметрами дифракционной картины (4). Эта связь выражается уравнениями:

Уравнения (5) применимы в области экрана наблюдения, определяемой условием:

где I(x, y) - интенсивность света, рассеянного в точке (x, y) на экране наблюдения. Область точек (x, y), описываемая соотношением (6), представляет собой эллиптическое кольцо, охватывающее центр ДК. В этой области градиент интенсивности рассеянного света близок к своему максимальному значению, а интенсивность рассеянного света примерно вдвое меньше интенсивности центрального дифракционного максимума. Решение уравнений (5) можно представить в виде:

где s - решение кубического уравнения имеет вид:

Используя условие (2), приближенные дифрактометрические уравнения можно представить в виде:

Решение уравнений (9) имеет вид:

Способ осуществляют следующим образом.

Чтобы измерить характеристики деформируемости эритроцитов, сначала с помощью фотоаппарата осуществляют видеозапись и обработку дифракционной картины, возникающей при рассеянии лазерного пучка на разбавленной суспензии эритроцитов, деформированных в сдвиговом потоке силами вязкого трения. Для достижения нужной концентрации следует цельную кровь разбавить вязкой жидкостью в 200-500 раз.

Затем с помощью компьютера оцифровывают эту дифракционную картину - для каждого пикселя светочувствительной матрицы фотоаппарата программно определяется значение яркости. Если лазер, освещающий частицы, - красный, то предпочтительно из цветовых компонент RGB (red, green, blue) каждого пикселя изображения дифракционной картины программно выбирают именно красную компоненту в качестве значения яркости света в данной точке, если лазер - зеленый, то зеленую компоненту и т.д. После этого определяют форму линии изоинтенсивности, лежащей в области дифракционной картины, где интенсивность рассеянного света примерно вдвое меньше интенсивности центрального дифракционного максимума, измеряют координаты полярных точек линии изоинтенсивности x_р и y_р, лежащие на пересечении данной линии изоинтенсивности с горизонтальной осью координат и с вертикальной осью координат, а также радиусы кривизны R(x_p) и R(y_p) данной линии изоинтенсивности в указанных полярных точках.

Далее вычисляют величины средней деформируемости эритроцитов s, дисперсии деформируемости эритроцитов μ и коэффициент асимметрии распределения эритроцитов по деформируемости ν по следующим формулам:

где:

х_р - координата полярной точки, лежащей на пересечении данной линии изоинтенсивности с горизонтальной осью координат (измеряется в мм);

y_р - координата полярной точки, лежащей на пересечении данной линии изоинтенсивности с вертикальной осью координат (измеряется в мм);

R(x_p) и R(y_p) - радиусы кривизны данной линии изоинтенсивности в указанных полярных точках (измеряются в мм).

Второй способ измерения параметров s, μ, ν осуществляют следующим образом. Сначала с помощью фотоаппарата осуществляют видеозапись и обработку дифракционной картины, возникающей при рассеянии лазерного пучка на разбавленной суспензии эритроцитов, деформированных в сдвиговом потоке силами вязкого трения. Для достижения нужной концентрации следует цельную кровь разбавить вязкой жидкостью в 200-500 раз.

Затем с помощью компьютера оцифровывают эту дифракционную картину - для каждого пикселя светочувствительной матрицы фотоаппарата программно определяется значение яркости. Если лазер, освещающий частицы, - красный, то предпочтительно из цветовых компонент RGB (red, green, blue) каждого пикселя изображения дифракционной картины программно выбирают именно красную компоненту в качестве значения яркости света в данной точке, если лазер - зеленый, то зеленую компоненту и т.д. После этого определяют форму линии изоинтенсивности, лежащей в области дифракционной картины, где интенсивность рассеянного света примерно вдвое меньше интенсивности центрального дифракционного максимума, измеряют координаты полярных точек линии изоинтенсивности x_р и y_р, лежащих на пересечении данной линии изоинтенсивности с горизонтальной осью координат и с вертикальной осью координат, а также радиусов кривизны R(x_p) и R(y_p) данной линии изоинтенсивности в указанных полярных точках.

Далее средняя деформируемость эритроцитов s находят путем решения кубического уравнения:

после чего дисперсию (ширину) деформируемости эритроцитов μ и коэффициент асимметрии распределения эритроцитов по деформируемости ν по следующим формулам

где:

Пример 1. Проверка предложенного способа методом численного моделирования

Для проверки работы данного способа было проведено численное моделирование и обработка ДК на компьютере. В качестве модели ансамбля эритроцитов использовали идеальный бимодальный ансамбль, в котором присутствуют клетки крови всего двух типов. Такой ансамбль описывается формами частиц обеих компонент ансамбля и долей частиц первого типа. Математически эти параметры определяются формулами

Используя уравнения бимодального ансамбля

и условие

нашли параметры

и ε₁, ε₂:

а также

Было рассмотрено три ансамбля частиц: унимодальный (однородный) ансамбль с параметром формы частиц

асимметричный бимодальный ансамбль с параметрами

и симметричный бимодальный ансамбль с параметрами

Для асимметричного ансамбля расчет по формулам (15), (16), (18) дает

а для симметричного ансамбля по формулам (15), (16), (19) получаем

Для удобства были введены величины:

Были сделаны численные расчеты ДК. Для однородного ансамбля такая картина описывается формулой (13)

Здесь x, y - декартовы координаты точки на экране наблюдения в системе координат, начало которой выбрано в центре ДК, z - расстояние от измерительного объема до экрана наблюдения, I₀ - интенсивность падающего лазерного пучка, N - число эритроцитов, облучаемых лазерным пучком, k=2π/λ - волновое число, λ - длина световой волны, J₁(x) - функция Бесселя первого порядка. Параметр определяется формулой , где Δϕ=k⋅n₀⋅h⋅(n-1), n - относительный показатель преломления эритроцита, n₀ - абсолютный показатель преломления окружающей его жидкости, a₁, b₁, h - геометрические размеры эллиптического диска, моделирующего эритроцит в сдвиговом потоке лазерного эктацитометра.

Ввели единицу измерения расстояния А и единицу измерения интенсивности света I₁ как

Тогда распределение интенсивности света (23) может быть представлено в виде:

где , и введены безразмерные переменные

На фигуре 3 показаны распределения интенсивности света по горизонтальной (А) и вертикальной (В) осям координат, построенные по формулам (17), (25), (26). Начало отсчета выбрано в центре дифракционной картины. Интенсивность света и координаты выражены в произвольных единицах.

Далее рассматривали бимодальный ансамбль частиц. Используя правило сложения интенсивностей, распределение интенсивности света в ДК для такого ансамбля запишем в виде:

Здесь a₁, b₁ и а₂, b₂ - размеры полуосей эллиптических дисков для частиц первого и второго типа, p - доля частиц первого типа в ансамбле частиц.

В безразмерных переменных (26) это распределение приобретает вид

Здесь параметр s₁ определен формулой (11). ДК, построенные с использованием формул (12), (14), (17), (20), (21), (25), (26), (28), показаны на фигуре 4. Здесь представлены картины для унимодального (А), асимметричного бимодального (В) и симметричного бимодального (С) ансамблей частиц, соответствующие им линии изоинтенсивности (D, Е, F) и круги кривизны линий изоинтенсивности в полярных точках (G, Н, I). Все линии изоинтенсивности соответствуют уровню интенсивности рассеянного света, равному 0.5 относительно интенсивности центрального дифракционного максимума (уровень 50 в единицах фигуры 2).

Полученные линии изоинтенсивности были обработаны с помощью алгоритма центра ДК, описанного выше. При этом были определены параметры s, μ' и ν', характеризующие, соответственно, среднюю форму частиц, дисперсию деформируемости эритроцитов и коэффициент асимметрии распределения эритроцитов по деформируемости частиц по формам. В частности, для асимметричного бимодального ансамбля частиц был получен следующий результат

Сравнивая данные (29) и (20), видим, что численный эксперимент подтверждает правильность работы предлагаемого способа.

Помимо этого был исследован вопрос о том, как влияют шумы дифракционной картины на качество работы способа. С этой целью к идеальному распределению интенсивности (28) в каждой точке экрана наблюдения был добавлен гауссовский шум с относительным стандартным отклонением, равным 5% или 10%. После этого было проведено сглаживание ДК с помощью процедуры бегущего среднего. При этом интенсивность света в каждой точке ДК находилась путем усреднения интенсивности по небольшой области экрана наблюдения вблизи данной точки. После был снова применен предлагаемый способ для измерения параметров распределения частиц по формам. Были получены следующие результаты. При уровне шума в 5% для асимметричного бимодального ансамбля частиц:

а при уровне шума в 10%

Таким образом, в условиях применения процедуры сглаживания ДК, предлагаемый способ обеспечивает достаточно высокую точность измерений даже при наличии шума.

Приведенный выше анализ работоспособности способов базировался на применении формулы (10) для расчета параметров s, μ, ν. Наряду с использованием упрощенной формулы (10), для вычисления аналогичных параметров были использованы также формулы (7-8). Сначала путем решения кубического уравнения было определено число s по формуле (7). Вычисления показали, что единственный действительный корень этого уравнения дает практические те же значения параметра s, что и в случае применения формулы (10). Подстановкой полученного числа s в формулы (8) были вычислены значения μ, ν. Они также практически совпали с результатом применения формулы (10).

Пример 2. Экспериментальная проверка способа на образцах человеческой крови

Для осуществления проверки анализы крови проводились на лазерном эктацитометре Rheoscan-AnD 300 (далее Реоскан). В этом приборе деформация эритроцитов происходит под действием сил вязкого трения в щелевом потоке (ширина щели около 200 микрон) при сдвиговых напряжениях от 0 до 20 Па. Устройство и принцип действия прибора Реоскан описаны в работе [Shin S., Ku Yu., Park M., Jang J., Suh J., Rapid cell-deformability sensing system based on slit-flow laser diffractometry with decreasing pressure differential, Biosensors and Bioelectronics, 20, pp. 1291-1297 (2005)].

Чтобы измерить характеристики деформируемости эритроцитов, сначала с помощью фотоаппарата, встроенного в Реоскан (разрешение 640×480 пикселей, в каждом пикселе сохраняются цвета Red Green Blue, по 8 бит памяти на каждую цветовую компоненту), была осуществлена видеозапись и обработка дифракционной картины, возникающей при рассеянии лазерного пучка на разбавленной суспензии эритроцитов, деформированных в сдвиговом потоке Реоскана силами вязкого трения. Для достижения нужной концентрации следует цельную кровь разбавить вязкой жидкостью в 200-500 раз.

Затем с помощью компьютера была оцифрована эта дифракционная картина - для каждого пикселя светочувствительной матрицы фотоаппарата было программно определено значение яркости. Лазер, освещающий частицы, - красный, поэтому из цветовых компонент RGB (red, green, blue) каждого пикселя изображения дифракционной картины посредством программы, написанной на языке Matlab (Mathworks software), была выбрана красная компонента в качестве значения яркости света в данной точке.

После этого была определена форма линии изоинтенсивности, лежащая в области дифракционной картины, где интенсивность рассеянного света примерно вдвое меньше интенсивности центрального дифракционного максимума.

После этого были измерены координаты полярных точек линии изоинтенсивности х_р [мм] и y_р [мм], а также радиусы кривизны линии в этих точках R(x_p) [мм] и R(y_p) [мм].

Далее были вычислены величины средней деформируемости эритроцитов s, дисперсии деформируемости эритроцитов μ и коэффициент асимметрии распределения эритроцитов по деформируемости ν по следующим формулам:

где

х_р - координата полярной точки, лежащей на пересечении данной линии изоинтенсивности с горизонтальной осью координат (измеряется в мм);

y_р - координата полярной точки, лежащей на пересечении данной линии изоинтенсивности с вертикальной осью координат (измеряется в мм);

R(x_p) и R(y_p) - радиусы кривизны данной линии изоинтенсивности в указанных полярных точках (измеряются в мм).

Для осуществления второго способа измерения параметров s, μ, ν были совершены следующие действия. Сначала с помощью фотоаппарата, встроенного в Реоскан (разрешение 640×480 пикселей, в каждом пикселе сохраняются цвета Red Green Blue, по 8 бит памяти на каждую цветовую компоненту), была осуществлена видеозапись и обработка дифракционной картины, возникающей при рассеянии лазерного пучка на разбавленной суспензии эритроцитов, деформированных в сдвиговом потоке Реоскана силами вязкого трения.

Затем с помощью компьютера была оцифрована эта дифракционная картина - для каждого пикселя светочувствительной матрицы фотоаппарата было программно определено значение яркости. Лазер прибора Реоскан, освещающий частицы, - красный, поэтому из цветовых компонент RGB (red, green, blue) каждого пикселя изображения дифракционной картины посредством программы, написанной на языке Matlab (Mathworks software), была выбрана красная компонента в качестве значения яркости света в данной точке. После этого была определена форма линии изоинтенсивности, лежащая в области дифракционной картины, где интенсивность рассеянного света примерно вдвое меньше интенсивности центрального дифракционного максимума.

Далее измеряли координаты полярных точек линии изоинтенсивности х_р и y_р, а также радиусы кривизны линии в этих точках R(x_p) и R(y_p).

Среднюю деформируемость эритроцитов s находили численно путем решения кубического уравнения:

после чего дисперсию деформируемости эритроцитов μ и коэффициент асимметрии распределения эритроцитов по деформируемости ν вычисляли по следующим формулам

В экспериментах использовали кровь здорового донора (мужчина, 25 лет), а также смеси нормальных эритроцитов с жесткими эритроцитами в разных пропорциях. Для приготовления жестких эритроцитов смешали 400 мкл эритромассы, 360 мкл физраствора и 240 мкл раствора глютаральдегида. Перемешали, выждали 5 минут. Анализ на Реоскане показал, что полученные таким образом эритроциты не деформируются в сдвиговом потоке.

Были исследованы три образца крови: нормальные эритроциты («унимодальный ансамбль»), а также смеси жестких и нормальных эритроцитов в соотношении 1:2 («асимметричный бимодальный ансамбль») и 1:1 («симметричный бимодальный ансамбль»). Применяя описанный выше алгоритм обработки данных, при определенном сдвиговом напряжении, вызывающем примерно двукратное удлинение нормальных эритроцитов. Были получены следующие результаты (таблица 1). Здесь для удобства были введены величины ,