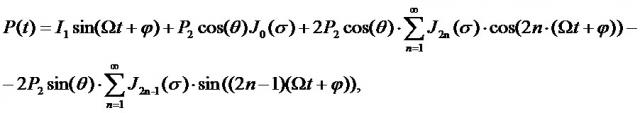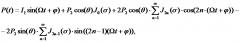Способ определения расстояния до объекта

Способ определения расстояния до объекта

Иллюстрации

Показать все

Реферат

Изобретение относится к области контрольно-измерительной техники, может быть использовано для определения расстояния до объекта с высокой точностью и может найти широкое применение в точном машиностроении и электронной технике.

Известен способ измерения расстояния, заключающийся в измерении расстояний с помощью проекционной оптической системы с базовым расстоянием между объективами каналов. В устройство введен осветительный канал для формирования зондирующей световой линии на поверхности объекта, две двухкоординатные ПЗС-матрицы, расположенные на фиксированных расстояниях от объективов, по одному направлению каждой из которых измеряются координаты точек объекта вдоль зондирующей световой линии, а по перпендикулярному направлению - параллаксы. Устройство также содержит встроенный контроллер для выработки координат энергетических центров изображений на ПЗС-матрицах точек объекта, освещенных световой линией, и для вычисления по значениям этих координат значений дальностей до освещенных точек объекта (см. патент на ИЗ № 2124700 МПК G01B11).

Недостатком известного способа и реализующих его устройств является использование сложной оптической системы, что затрудняет работу данной разработки в малогабаритных технологических установках.

Известен способ измерения расстояния, в котором облучение измеряемого объекта происходит через оптическую фокусирующую систему моноимпульсным лазерным излучателем с модулированной добротностью и плотностью мощности в точке фокусировки, для получения поправки на текущую скорость звука используют компаратор с мерной базой, а излучение фокусируют в точке измерения объекта и одновременно в двух точках мерной базы, звуковой сигнал принимают с помощью широкополосной акустической антенны, причем точки облучения, а также приемник и его антенну располагают на оптической оси фокусирующей системы, а отсчет времени приема звуковой волны производят в конце первого полупериода электрического сигнала приемника, индуцированного этой волной. Устройство для осуществления способа содержит оптическую фокусирующую систему лазерного излучателя и компаратор с мерной базой, приемник акустических сигналов содержит широкополосную высокочастотную антенну, при этом оси антенны, акустического приемника и мерной базы совмещены с оптической осью фокусирующей системы (см. патент на ИЗ № 2267743 МПК G01B11).

Недостатком известного способа является то, что в измерительной системе используется источник акустических волн, который способен вызвать дополнительные вибрации, влияющие на объект измерений, например тонкостенные оболочки. Подобные вибрации будут служить дополнительным источником погрешности при измерении расстояния.

Известен способ и устройство для измерения расстояния, в котором излучение от лазерного диода после прохождения линзы падает на поверхность объекта в виде поплавка, покрытого отражающей лентой. Отражённый от объекта луч возвращается обратно в блок лазерного диода и регистрируется фотодиодом. Анализируя зарегистрированный сигнал, определяют расстояние L от измерителя до объекта (см. патент на ИЗ № 2101731 МПК G01S17).

Недостатком известного способа является то, что этот способ измерения сильно зависит от величины отражённого оптического излучения. Для того чтобы сигнал отражался от поверхности, авторы изобретения используют специальную ленту. Использование подобной ленты на некоторых объектах, со сложной геометрией и шероховатостью, представляется затруднительным.

Наиболее близким к предлагаемому решению является способ измерения расстояния, в котором используется полупроводниковый лазерный диод со средством возбуждения, обеспечивающим изменение рабочей частоты лазера. При измерении луч от лазера, в виде последовательности импульсов, направляют на поверхность объекта, расстояние до которого требуется найти. Отражённое от объекта излучение имеет интенсивность, связанную с расстоянием от лазерного диода до цели, обусловленную когерентной интерференцией в лазере между рассеянным светом от объекта и светом внутри лазерного диода. Детектирование этого сигнала обеспечивает выработку электрического сигнала обратной связи. Сигнал содержит информацию об импульсах интенсивности, связанных с расстоянием L до объекта. По количеству импульсов рассчитывают расстояние до объекта, используя расчётное соотношение (см. патент РФ на изобретение № 2111510 МПК G01S17).

Недостатком известного способа является то, что в системе необходимо использование дополнительного блока, обеспечивающего гашение части сигнала обратной связи для уменьшения воздействия разрывов непрерывности сигнала возбуждения лазера на показания измерителя расстояния.

Задача настоящего способа заключается в определении расстояния до объекта по спектру частотно-модулированного полупроводникового лазерного автодинного интерферометра.

Технический результат заключается в значительном повышении точности измерения амплитуды нановибраций объекта.

Поставленная задача решается за счет того, что освещают объект лазерным излучением, отраженное от объекта излучение, интерферирующее в лазере, преобразуют в электрический автодинный сигнал, отличающийся тем, что лазерное излучение частотой ω₀ модулируют по гармоническому закону с частотой ν посредством модуляции тока питания лазера, что приводит к изменению длины волны излучения на величину Δλ, фильтруют амплитудную составляющую автодинного сигнала на частоте ν, раскладывают сигнал в спектральный ряд, измеряют амплитуду 2n-й (C_2n) и 2n+2-й (C_2n+2) гармоник спектра или 2n+1-й (C_2n+1) и 2n+3-й (C_2n+3) гармоник спектра автодинного сигнала, по зависимости или соответственно, вычисляют значение аргумента функции Бесселя первого рода σ из соотношений

где , – параметр токовой модуляции лазерного автодина (девиация частоты излучения лазерного диода), а расстояние до объекта L находят по формуле .

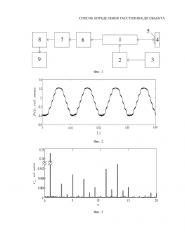
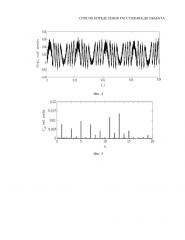
Изобретение поясняется чертежами. На фиг. 1 представлена схема экспериментальной установки; на фиг. 2 и 3 представлены частотно-модулированный автодинный сигнал, полученный на экспериментальной установке при изменении длины волны излучения лазерного диода нм, и его спектр соответственно, где n – номер гармоники; на фиг. 4 и 5 представлены автодинный сигнал после фильтрации на модулирующей частоте ν, полученный на экспериментальной установке при изменении длины волны излучения лазерного диода на нм, и его спектр соответственно, где n – номер гармоники. Позициями на чертежах обозначены:

1 – полупроводниковый лазер,

2 – блок управления током питания,

3 – генератор сигналов на базе платформы NI ELVIS,

4 – микромеханическая подача,

5 – объект,

6 – фотоприемник,

7 – фильтр переменного сигнала,

8 – аналого-цифровой преобразователь (АЦП),

9 – компьютер.

Теоретическое обоснование способа.

Для определения расстояния до объекта по спектру частотно-модулированного автодинного сигнала используют следующие теоретические предпосылки.

При воздействии отраженного излучения от объекта на лазерный диод излучаемая им мощность может быть определена в результате использования малосигнального анализа дифференциальных уравнений для комплексного электрического поля с запаздывающим аргументом и концентрации носителей заряда и записана в виде (Усанов Д.А., Скрипаль А.В., Авдеев К.С. Определение расстояния до объекта с помощью частотно-модулированного полупроводникового лазерного автодина // Письма в ЖТФ. 2007. Том 33. Вып 21. С. 72-77)

(1)

где - составляющая мощности, независящая от расстояния до внешнего отражателя, – амплитудная составляющая мощности, зависящей от фазового набега волны в системе с внешним отражателем, – время обхода лазерным излучением расстояния до внешнего отражателя, – частота излучения полупроводникового лазера, зависящая от плотности тока накачки и уровня обратной связи.

При модуляции длины волны излучения полупроводникового лазера частота и амплитудная составляющая мощности излучения лазера определятся соотношениями

(2)

(3)

где – собственная частота излучения полупроводникового лазерного диода; – девиация частоты излучения полупроводникового лазерного диода; - изменение длины волны излучения при модуляции тока питания лазерного диода ; – частота модуляции тока питания лазерного диода; – начальная фаза. – амплитуда токовой модуляции составляющей .

Для описания низкочастотного спектра автодинного сигнала при гармонической модуляции длины волны излучения лазерного диода мощность автодинного сигнала может быть представлена в соответствии с (Усанов Д.А., Скрипаль А.В., Авдеев К.С. Определение расстояния до объекта с помощью частотно-модулированного полупроводникового лазерного автодина // Письма в ЖТФ. 2007. Том 33. Вып 21. С. 72-77) в виде разложения в ряд по функциям Бесселя первого рода :

(4)

где , , . Представляя автодинный сигнал в виде ряда Фурье с коэффициентами разложения и :

(5)

Коэффициенты , равные по модулю четным и нечетным спектральным составляющим разложения в ряд Фурье

(6)

(7)

можно записать в виде:

(8)

для четных n: (9)

для нечетных n: (10)

Соотношения (8) – (10) характеризуют связь спектральных составляющих частотно-модулированного автодинного сигнала с функциями Бесселя первого рода.

Для определения расстояния до объекта , входящего в параметр , используем известные отношения 2n и 2n+2 спектральных гармоник и отношение 2n+1 и 2n+3 спектральных гармоник:

(11)

(12)

Решение полученных уравнений (11) и (12) относительно неизвестного параметра требует знания параметров токовой модуляции лазерного автодина, в частности девиации частоты излучения лазерного диода. Принимая во внимание, что , получаем соотношение для определения расстояния до объекта:

(13)

Способ реализуется следующим образом.

Схема экспериментальной установки представлена на фиг.1. Освещают объект 5, закрепленный на микромеханической подаче 4, излучением от полупроводникового лазерного диода 1 на квантоворазмерных структурах с дифракционно-ограниченной одиночной пространственной модой RLD-650(5) с длиной волны 654 нм, длина волны излучения лазера модулируется посредством гармонического изменения тока питания лазера с помощью встроенного в платформу NI ELVIS генератора сигналов 3, изменение тока питания лазерного диода осуществляется путем изменения напряжения питания, подаваемого на блок управления током питания 2, преобразуют отраженное от объекта излучение в электрический автодинный сигнал с помощью фотодетектора 6, через фильтр переменного сигнала 7, аналого-цифровой преобразователь 8, подают сигнал на компьютер 9, осуществляют фильтрацию амплитудной составляющей автодинного сигнала и преобразованный электрический сигнал раскладывают в спектральный ряд, измеряют амплитуду 2n-й (C_2n) и 2n+2-й (C_2n+2) гармоник спектра или 2n+1-й (C_2n+1) и 2n+3-й (C_2n+3) гармоник спектра автодинного сигнала. По зависимости или соответственно, вычисляют значение аргумента функции Бесселя первого рода σ, расстояние до объекта L находят по формуле .

Практическая реализация способа осуществлялась следующим образом.

Длина волны излучения полупроводникового лазера модулировалась с частотой 200 Гц посредством гармонического изменения тока питания лазера с помощью встроенного в платформу NI ELVIS генератора сигналов. Эффективная модуляция тока питания лазерного диода наблюдалась при амплитуде модулирующего сигнала 50 мВ.

На фиг. 2 представлен частотно-модулированный автодинный сигнал, полученный на экспериментальной установке при изменении длины волны излучения лазерного диода нм. В спектре сигнала (фиг.3) для измерений были выбраны 13 и 15 гармоники с амплитудами С₁₁= 0.0117 и С₁₃=0.0137.

На фиг. 4 представлен автодинный сигнал после фильтрации амплитудной составляющей автодинного сигнала на частоте ν, полученный на экспериментальной установке при изменении длины волны излучения лазерного диода на нм. Вид автодинного сигнала в данной конфигурации совпадает с видом автодинного сигнала, полученного при измерении амплитуды микро- и нановибраций объекта, без использования изменения длины волны излучения лазерного диода, посредством токовой модуляции (Усанов Д.А., Скрипаль А.В. Полупроводниковые лазерные автодины для измерения параметров движения при микро- и наносмещениях. — Саратов: Изд-во Сарат. ун-та, 2014. - 136 с.). Идентичность форм автодинных сигналов позволила применить соотношения, используемые для определения функции Бесселя первого рода σ при измерении амплитуд микро- и нановибраций объекта, для повышения точности определения расстояния до объекта, используя модуляцию длины волны лазерного излучения.

В спектре автодинного сигнала (фиг. 5), представленного на фиг. 4, для измерений были выбраны 13 и 15 гармоники с амплитудами С₁₃= 0.0117 и С₁₃=0.0137.

Рассчитанное значение σ составило σ=14.13.

Зная величину σ, определяем амплитуду колебаний отражателя из соотношения

.

Расстояние до объекта, вычисленное по нескольким наборам спектральных составляющих автодинного сигнала после его фильтрации, представленного на фиг. 4, составило L=0.215 м, а значение погрешности – 1.2%.

Способ измерения расстояния до объекта, заключающийся в том, что освещают объект лазерным излучением, отраженное от объекта излучение, интерферирующее в лазере, преобразуют в электрический автодинный сигнал, отличающийся тем, что лазерное излучение частотой ω₀ модулируют по гармоническому закону с частотой ν посредством модуляции тока питания лазера, изменяют длину волны излучения на величину Δλ, фильтруют амплитудную составляющую автодинного сигнала на частоте ν, раскладывают сигнал в спектральный ряд, измеряют амплитуду 2n-й (C_2n) и 2n+2-й (C_2n+2) гармоник спектра или 2n+1-й (C_2n+1) и 2n+3-й (C_2n+3) гармоник спектра автодинного сигнала, по отношению или соответственно, вычисляют значение аргумента функции Бесселя первого рода σ из соотношений или где , – параметр токовой модуляции лазерного автодина (девиация частоты излучения лазерного диода), а расстояние до объекта L находят по формуле .