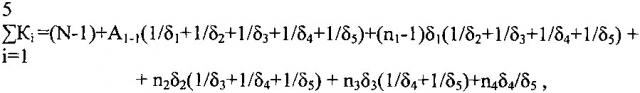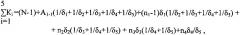Универсальный набор концевых мер

Универсальный набор концевых мер

Иллюстрации

Показать все

Реферат

Изобретение относится к области механических средств измерения, а именно к приспособлениям для измерения определенных параметров деталей (длины, ширины, толщины и т.п.), конкретно - к наборам концевых мер, и может быть использовано в различных отраслях машиностроения, например в производстве инструментов, в сборочном производстве при измерении зазоров, при настройке стрелочных измерительных приборов и др.

Известен универсальный набор концевых плоскопараллельных мер №1 по стандарту [1. ГОСТ 9038-90. Меры длины концевые плоскопараллельные: Технические условия. Введ. 01.07.1991. Группа П51], состоящий из нескольких групп мер с общим числом - 83 меры с наименьшей и наибольшей мерами, равными 0,5 мм и 100 мм соответственно. Недостатками набора являются завышенные количество мер и масса набора.

Наиболее близким к предлагаемому решению является универсальный набор концевых плоскопараллельных мер по патенту [2. Пат. №2529662 RU, МПК G01B 5/02. Универсальный набор концевых мер / Фот А.П., Чепасов В.И., Лисицкий И.И. - Опубл. 27.09.2014. Бюл. №27], состоящий из пяти групп мер, причем первая мера первой группы является наименьшей мерой A_1-1 набора, размер последней меры A_n1-1 первой группы подчинен зависимости:

где n₁ - количество мер и δ₁ - шаг размеров мер в первой группе, а размеры всех мер набора начиная со второй группы взаимосвязаны и подчинены зависимостям:

и

где A_1-m - размер первого элемента группы с номером «m»;

A_n-(m-1) и δ_(m-1) - размер последнего элемента и шаг размеров группы с номером «m-1»;

A_nm-m, n_m и δ_m - размер последнего элемента, количество элементов и шаг размеров группы с номером «m», отличающийся тем, что количество элементов в группах подчинено зависимостям:

где n₁ и n_m - количество элементов первой группы и группы с номером «m» соответственно;

К₁, K_(m-1) и K_m - отношения значения размера последнего элемента группы к значению шага размеров данной группы для первой группы, групп с номером «m-1» и с номером «m» соответственно;

A₁₁ - размер первого элемента первой группы набора;

δ₁, δ_(m-1) и δ_m - шаг размеров элементов первой группы, групп с номером «m-1» и с номером «m» соответственно, причем значения отношений К₁, К₂, … К₅ находятся в интервалах целых натуральных чисел 100≤K₁≤201, 51≤К₂≤150, 8≤К₃≤20, 5≤К₄≤50, 1≤К₅≤10), подчинены зависимости:

и удовлетворяют условию:

где N - общее количество элементов в наборе, N=n₁+n₂+n₃+n₄+n₅.

Недостатками набора являются завышенные количество мер и масса набора.

Цель изобретения - повышение эффективности набора за счет уменьшения количества мер и массы набора, а также расширения технологических возможностей: расширение границ ряда размеров составленных блоков и увеличение количества размеров составленных блоков с заданным шагом.

Поставленная задача достигается тем, что в универсальном наборе концевых мер, состоящем из пяти групп мер, первая мера первой группы является наименьшей мерой А_1-1 набора, размер последней меры A_1-n1 первой группы подчинен зависимости:

где n₁ и δ₁ - количество мер и шаг размеров мер в первой группе. Количество мер в первой группе подчинено зависимости:

где

Размеры всех мер набора начиная со второй группы взаимосвязаны и отличаются тем, что подчинены зависимостям:

и

где A_1-m - размер первой меры группы с номером «m»;

A_n-(m-1) - размер последней меры группы с номером «m-1»;

A_nm-m, n_m и δ_m - размер последней меры, количество мер и шаг размеров мер группы с номером «m»; значения шагов δ₁…δ₅ размеров мер в группах определены рядом 1:10:20:200:2000 относительно размера шага мер в первой группе, а количество мер в группах подчинено зависимости:

причем K_m и K_(m-1) - значения отношений размеров последних мер групп с номерами «m» и «m-1» соответственно к значению шага размеров в группе с номером «m» - целые натуральные числа в интервалах 100≤K₁≤150, 12≤К₂≤62, 7≤К₃≤57, 2≤К₄≤52, 1≤К₅≤10 для групп 1…5 соответственно и удовлетворяющие условию:

где N=n₁+n₂+n₃+n₄+n₅.

Реализация решения (проектирование набора) осуществляется в следующем порядке: назначение исходных данных; определение количества мер в группах; определение размеров мер набора; определение характеристик набора.

В качестве примера предлагается вариант решения:

1) Задаем значение размера первой меры первой группы А₁₁=0,5 мм;

2) Задаем значения шагов размеров мер в группах набора, мм:

δ₁=0,005; δ₂=0,050; δ₃=0,100; δ₄=1,000; δ₅=10,000;

3) Задаем для каждой группы величины отношений значения размера последнего элемента группы к значению шага размеров данной группы (из рекомендуемых интервалов): К₁=120, К₂=18, К₃=20, К₄=10 и К₅=10;

4) Определяем значения количества мер в группах n_1…5 и размеры последних мер в каждой группе, используя предложенные зависимости (8, 9, 11, 13):

A_1-n1=А_1-1+(n₁-1)δ₁, n₁=К₁-А_1-1/δ₁+1, A_1-m=A_n-(m-1)+δ_m и n_m=K_m-K_(m-1):

n₁=К₁-A_1-1/δ₁+l=120-0,5/0.005+1=21;

А_21-1=А_1-1+(n₁-1)δ₁=0,5+(21-1)0,005=0,6;

n₂=K_m-K_(m-1)=18-0,6/0,05=6;

А_6-2=A_1-2+(n₂-1)δ₂=A_21-1+δ₂+(n₂-1)δ₂=0,6+0,05+(6-1)0,05=0,9;

n₃=K_m-K_(m-1)=20-0,9/0,1=11;

А_11-3=А_1-3+(n₃-1)δ₃=А_6-2+δ₃+(n₃-1)δ₃=0,9+0,1+(11-1)0,1=2;

n₄=K_m-K_(m-1)=10-2/1=8;

А_8-4=А_1-4+(n₄-1)δ₄=А_11-3+δ₄+(n₄-1)δ₄=2+1+(8-1)=10;

n₅=K_m-K_(m-1)=10-10/10=9;

А_9-5=А_1-5+(n₅-1)δ₅=А_8-4+δ₅+(n₅-1)δ₅=10+10+(9-1)10=100;

5) Определяем общее количество мер набора N как сумму количества мер в группах: N=n₁+n₂+n₃+n₄+n₅=21+6+11+8+9=55;

6) Производим проверку условия ΣK_i:

В левой части равенства:

ΣK_i=K₁+K₂+К₃+К₄+К₅=120+18+20+10+10=178;

В правой части равенства:

Поскольку левая и правые части равны, условие выполняется.

7) Определяем размеры остальных мер набора, используя предложенные зависимости 8, 11, 12:

A_1-n1=A_1-1+(n₁-1)δ₁,

A_1-m=A_n-(m-1)+δ_m,

A_nm-m=A_1-m+(n_m-1)δ_m.

Без промежуточных вычислений приведены размеры мер по группам:

- группа 1: 0,5; 0,505; 0,51; 0,515; 0,52; 0,525; 0,53; 0,535; 0,54; 0,545; 0,55; 0,555; 0,56; 0,565; 0,57; 0,575; 0,58; 0,585; 0,59; 0,595; 0,6;

- группа 2: 0,65; 0,7; 0,75; 0,8; 0,85; 0,9;

- группа 3: 1; 1,1; 1,2; 1,3; 1,4; 1,5; 1,6; 1,7; 1,8; 1,9; 2,0:

- группа 4: 3; 4; 5; 6; 7; 8; 9; 10;

- группа 5: 20; 30; 40; 50; 60; 70; 80; 90; 100.

Если в исходных данных на проектирование набора вводится ограничение на общее количество мер N в наборе, то расчет становится многовариантным и выбор значений K₁…K_m производится с использованием ЭВМ по специальной программе. Программа дает несколько вариантов сочетаний К₁…K_m, для каждого из которых производится формирование наборов и определение их технических характеристик, а выбор оптимального набора производится сравнением характеристик.

Для оценки эффективности предлагаемого решения (табл. 1) произведено сравнение его с двумя вариантами наборов: базовым универсальным набором из 83 мер по стандарту [1.] (табл. 2) и набором из 83 мер по прототипу [2.] (табл. 3).

Для сравнительной оценки наборов используем следующие характеристики (табл. 4):

- СДМ - суммарная длина мер набора;

- МСР - минимальный составленный размер непрерывного ряда размеров, составленных из мер блоков;

- НСР - наибольший составленный размер непрерывного ряда размеров составленных блоков (не более чем из 5-ти мер);

- КСР - количество составленных размеров непрерывного ряда размеров составленных блоков;

- УПК - условный показатель качества набора (количество составленных размеров непрерывного ряда на единицу длины набора).

Каждой характеристике присваивается значение ранга от 1 до 3 (худшее значение характеристики имеет меньшее значение ранга).

Данные Таблицы 4 подтверждают достижение заявленного технического результата:

- повышение эффективности набора по сравнению с прототипом за счет уменьшения количества мер на 28 (с 83-х до 55-ти);

- уменьшение массы набора вследствие уменьшения суммарной длины мер на 8,4%;

- расширение технологических возможностей: расширение границ ряда размеров составленных блоков на 0,41 мм и увеличение количества размеров составленных блоков с заданным шагом на 82 размера.

Предлагаемый набор может быть выполнен с помощью стандартного оборудования и материалов отечественного производства. Таким образом, заявленное устройство соответствует критерию «промышленная применимость».

Источники, принятые во внимание

1. ГОСТ 9038-90. Меры длины концевые плоскопараллельные: Технические условия. Введ. 01.07.1991. Группа П51.

2. Пат. №2529662 RU. МПК G01B 5/02. Универсальный набор концевых мер / Фот А.П., Чепасов В.И., Лисицкий И.И. - Опубл. 27.09.2014. Бюл. №27.

3. Пат. 2392580 RU. МПК G01B 3/30, G01B 5/02. Набор концевых мер / Фот А.П., Муллабаев А.А., Чепасов В.И., Лисицкий И.И. - Опубл. 20.06.2010.

4. Пат. 2307996 RU. МПК G01B 3/30, G01B 5/02. Набор концевых мер и щупов / Фот А.П., Муллабаев А.А., Лисицкий И.И. - Опубл. 10.10.2007.

Универсальный набор концевых мер, состоящий из пяти групп мер, причем первая мера первой группы является наименьшей мерой A_1-1 набора, размер последней меры A_1-n1 первой группы подчинен зависимости

A_1-n1=A_1-1+(n₁-1)δ₁,

где n₁ и δ₁ - количество мер и шаг размеров мер в первой группе, количество мер в первой группе подчинено зависимости

n₁=K₁-A_1-1/δ₁+1, где

K₁=A_1-n1/δ₁,

размеры всех мер набора взаимосвязаны, отличающийся тем, что начиная со второй группы:

- размеры мер подчинены зависимостям:

A_1-m=A_n-(m-1)+δ_m,

A_nm-m=A_1-m+(n_m-1)δ_m,

где A_1-m - размер первой меры группы с номером «m»;

A_n-(m-1) - размер последней меры группы с номером «m-1»;

A_nm-m, n_m и δ_m - размер последней меры, количество мер и шаг размеров мер группы с номером «m»;

- значения шагов δ₁…δ₅ размеров мер в группах определены рядом 1:10:20:200:2000 относительно размера шага мер в первой группе;

- количество мер в группах подчинено зависимости

n_m=K_m-K_(m-1),

причем K_m и K_(m-1) - значения отношений размеров последних мер групп с номерами «m» и «m-1» соответственно к значению шага размеров в группе с номером «m», причем K₁…K₅ - целые натуральные числа в интервалах 100≤K₁≤150, 12≤K₂≤62, 7≤K₃≤57, 2≤K₄≤52, 1≤K₅≤10 для групп 1…5 соответственно и удовлетворяющие условию

где N=n₁+n₂+n₃+n₄+n₅.