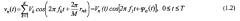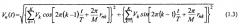Способ передачи информации многочастотными сигналами методом адаптивного масштабирования и ограничения

Способ передачи информации многочастотными сигналами методом адаптивного масштабирования и ограничения

Иллюстрации

Показать все

Реферат

Область техники, к которой относится изобретение

Изобретение относится к технике электрической связи и может быть применено для передачи информации многочастотными сигналами, например, в системах связи на основе OFDM-технологии (Orthogonal Frequiency Division Multiplexing - мультиплексирование с ортогональным частотным разделением).

Уровень техники

Известен способ передачи информации многочастотными сигналами, состоящий из преобразования последовательности информационных символов в комбинацию модулирующих символов, формирования многочастотного сигнала в виде суммы парциальных сигналов различных частот, каждый из которых модулирован соответствующим модулирующим символом и усиления мощности (Системы цифровой радиосвязи: базовые методы и характеристики: Учеб. пособие / Л.Н. Волков, М.С. Немировский, Ю.С. Шинаков. - М.: Эко-Трендз, 2005. - 392 с), называемый далее способ-аналог.

На фиг. 1 приведена структура алгоритма способа-аналога. Сформированный многочастотный сигнал ν_n(t) является суммой K модулированных М-ичными символами r_nk парциальных сигналов ν_nk(t). Всего возможно N различных комбинаций модулирующих символов, порождающих ансамбль сигналов объемом N. Объем ансамбля не может превышать величины M^K. Если N равно M^K, то ансамбль является полным кодом, т.е. модулирующие символы могут образовывать все возможные комбинации. Индекс n обозначает порядковый номер (например, в десятичной системе счисления) комбинации в полном коде.

В системах связи на основе OFDM-технологии устранение межканальной интерференции символов в приемнике достигается ортогональностью парциальных сигналов ν_nk(t) на интервале времени длительностью Т, для чего их частоты ƒ_k должны образовывать арифметическую прогрессию с постоянной разностью Δƒ=1/Т:

где - частота первого парциального сигнала;

g₁ - целое число, равное числу периодов частоты ƒ₁ на интервале Т.

Сигнал ν_n(t) имеет переменную огибающую даже при постоянных огибающих парциальных сигналов, что имеет место при фазовой (ФМ) или относительной фазовой (ОФМ) модуляции:

где V_k - амплитуда k-го парциального сигнала;

V_n(t) - огибающая сигнала ν_n(t):

Ψ_n(t) - фаза сигнала ν_n(t).

Огибающая и фаза в (1.2) определяются следующими соотношениями:

Усилитель мощности многочастотных сигналов должен быть таким, чтобы при усилении гармонического сигнала с амплитудой V_max он не вносил существенных нелинейных искажений. Тогда сигналы на его входе ν_n(t) и выходе u_n(t), их огибающие V_n(t) и U_n(t) с точностью до постоянного множителя совпадают, т.е. они пропорциональны. Следовательно, выходные сигналы ортогональны и имеют те же пик-факторы, что и входные:

где - пиковое значение огибающей V_n(t);

- наибольшее пиковое значение огибающей;

- пиковое значение огибающей U_n(t);

V_{n sqr}U_{n sqr} - среднеквадратичные значения огибающих V_n(t), U_n(t);

P_{n max}=0,5U_{n max} - пиковая мощность сигнала u_n(t);

- мощность сигнала u_n(t).

Наибольшему пиковому значению V_max входного сигнала соответствует наибольшее пиковое значение U_max сигнала на выходе усилителя и его мощность P_pek должна соответствовать пиковой мощности этого сигнала:

При использовании ФМ, ОФМ для любых значений K и М наибольшее пиковое значение огибающей, как следует из (1.2), равно значению сигнала в момент времени t=0 при равенстве нулю всех модулирующих символов:

где - наибольшая амплитуда парциального сигнала;

ν_k=V_k/V - нормированная амплитуда k-го парциального сигнала.

При использовании ФМ, ОФМ максимальный пик-фактор ограничен сверху:

Нестрогое равенство в правой части (1.7, 1.8) обращается в строгое при одинаковых амплитудах парциальных сигналов, т.е. когда они равномощны.

На фиг. 2 приведена гистограмма пик-факторов полного кода равновероятных, равномощных сигналов с двоичной модуляцией фазы (K=8).

Мощность сигнала на выходе усилителя равна сумме мощностей P_nk парциальных сигналов в силу их ортогональности:

где U_nk - амплитуда k-го парциального сигнала n-й реализации сигнала.

Из (1.9) и (1.5) следует, что при использовании ФМ, ОФМ мощность любой реализации сигнала на выходе усилителя неизменна и в П_max раз меньше пиковой мощности усилителя:

Нестрогое равенство в правой части (1.10) обращается в строгое для равномощных парциальных сигналов. Тогда мощность каждого из них в K² раз меньше пиковой мощности усилителя:

Как видно из (1.10, 1.11), недостатком способа-аналога является низкое использование пиковой мощности усилителя.

Эффективность усиления мощности характеризуется коэффициентом полезного действия (КПД) усилителя как отношения мощности сигнала на выходе усилителя к мощности, потребляемой усилителем от источника питания.

КПД двухтактного усилителя мощности в режиме класса В при усилении гармонического сигнала равен (Усилительные устройства. Учебное пособие для вузов / И.Г. Мамонкин. - Изд. 2-е, перераб. и доп. - М.: Связь. 1977. - 360 с.):

где U_E - напряжение источника питания усилителя;

U_a=U_E-ΔU - амплитуда гармонического сигнала на выходе усилителя:

ΔU - падение напряжения на активных элементах усилителя.

Пропорциональность между входными и выходными сигналам усилителя будет соблюдаться, если напряжение источника питания удовлетворяет условию:

Тогда потребляемый от источника питания ток будет пропорционален 2U_n(t)/π и потребляемая мощность является функцией времени:

Эффективность усиления сигнала характеризуется локальным КПД как отношение мощности сигнала на выходе усилителя к среднему значению потребляемой мощности:

где V_nT, U_nT - средние значения огибающих V_n(t), U_n(t).

Среднеквадратичные значения всех огибающих одинаковы при использовании ФМ, ОФМ и локальный КПД в этом случае равен:

В силу неравенства Коши-Буняковского (неравенство Шварца) среднее значение огибающей меньше среднеквадратичного значения и из (1.16) следует неравенство:

Неравенство (1.17) справедливо для всех локальных КПД. поэтому величина η_i, является строгой нижней границей минимального КПД при усилении многочастотных сигналов с ФМ, ОФМ.

Из (1.15) видно, что локальный КПД достигает максимума, если V_{n max}=V_max. При использовании ФМ, ОФМ это имеет место для сигналов ν_n(t) с максимальным пик-фактором. Одной из таких реализаций является реализация ν₀(t) с огибающей V₀(t) и КПД при усилении этой реализации с равномощными парциальными сигналами:

где - среднее значение функции V₀(t)/V.

При усилении многочастотных сигналов с ФМ, ОФМ локальный КПД находится в границах:

Эффективность усиления ансамбля сигналов характеризуется средним КПД как математического ожидания всех локальных КПД:

где m₁〈⋅〉 - операция математического ожидания.

На фиг. 3 приведена гистограмма локальных КПД при усилении полного кода равновероятных, равномощных сигналов с двоичной модуляцией фазы для способа-аналога (K=8 δ_U=0). Максимальный КПД η_max=42,9%, средний - η_med=31,4%, минимальный - η_min=28,7%, что на 0,9% выше нижней границы η_i=27.8%. Способ-аналог характеризуется низкими значениями КПД, что также является его недостатком.

Наиболее близким к заявляемому изобретению является способ передачи информации многочастотными сигналами, состоящий из преобразования последовательности информационных символов в комбинацию модулирующих символов, формирования много-частотного сигнала в виде суммы ортогональных парциальных сигналов различных частот, каждый из которых модулирован по фазе соответствующим модулирующим символом, масштабирования суммарного сигнала путем его умножения на коэффициент масштабирования, ограничения масштабированного сигнала и усиления мощности (Аппаратура передачи дискретной информации МС-5. Под ред. A.M. Заездного, Ю.Б. Окунева. - М.: Связь. 1970. 152 с.), называемый далее способ-прототип. На фиг. 4 приведена структура алгоритма способа-прототипа. В способе-прототипе сформированный сигнал ν_n(t) масштабируют, умножая его на коэффициент масштабирования y₀. Результатом масштабирования является увеличение в y₀ раз пиковых, средних и среднеквадратичных значений исходных сигналов и их огибающих. Масштабированный сигнал y₀ν_n(t) в результате ограничения преобразует в сигнал s_n(t) с огибающей S_n(t):

где V_s - порог ограничения.

На фиг. 5 приведены графики сигналов на входе, выходе ограничителя, огибающая ограниченного сигнала.

Ограничение отсутствует для тех сигналов, у которых увеличенное в у₀ раз пиковое значение огибающей не превышает порога ограничения:

В способе-прототипе каждый парциальный сигнал модулируют по фазе, поэтому среднеквадратичные значения всех сформированных сигналов одинаковы (ν_{n sqr}=ν_sqr) и эквивалентное соотношению (2.3) условие отсутствия ограничения, выраженное через пик-фактор сигнал:

где X_s=V_s/V_sqr - относительный порог ограничения.

Заданием порога ограничения и коэффициента масштабирования множество всех усиливаемых сигналов разделяют на два подмножества. Первое подмножество (подмножество А) состоит из сигналов, не подвергающихся ограничению, т.е. сигналов с пик-фактором не превышающего критического значения П_s. Второе подмножество (подмножество В) состоит из сигналов, подвергающихся ограничению, т.е. сигналов с пик-фактором выше критического значения. Очевидно, что при П_s>П_max все сигналы не ограничиваются, а при П_s>П_min - ограничиваются. На фиг. 6 приведена зависимость П_s=φ_П(y₀,X_s) для полного кода равновероятных, равномощных сигналов с двоичной модуляцией фазы в способе-прототипе (K=8).

В способе-прототипе усилитель мощности выбирают таким, чтобы при усилении гармонического сигнала амплитудой, равной порогу ограничения V_s, он не вносил существенных нелинейных искажений. Тогда сигналы на его входе s_n(t) и выходе u'_n(t). их огибающие S_n(i), U'_n(t) пропорциональны и пиковая мощность усилителя P'_pek может быть снижена относительно пиковой мощности усилителя P_pek в способе-аналоге:

где U_s - амплитуда выходного сигнала, соответствующая амплитуде V_s.

Следовательно, напряжение источника питания усилителя в способе-прототипе должно быть:

где ΔU' - падение напряжения на активных элементах усилителя, Тогда при усилении сигналов подмножества А их мощность равна сумме мощностей парциальных сигналов, каждая из которых в раз больше, чем в способе-аналоге:

Увеличение мощности уменьшает вероятность ошибки приема этих сигналов в способе-прототипе относительно способа-аналога.

Потребляемая усилителем мощность и локальный КПД при усилении сигналов подмножества А:

Соответствующим выбором активных элементов усилителя в способе-прототипе можно обеспечить соизмеримость величины δ'_U с величиной δ_U в способе-аналоге. Тогда из сравнения (2.9) с (1.16) следует, что локальный КПД при усилении сигналов подмножества А выше локального КПД при усилении тех же сигналов в способе-аналоге:

Ток, протекающий через активные элементы усилителя мощности класса В, имеет форму половин косинусоидальных импульсов с амплитудой I_a, пропорциональной амплитуде V_a напряжения входного гармонического сигнала с частотой ƒ_a.

При ограничении входного гармонического сигнала на уровне V_s ток имеет вид усеченных на уровне I_s половин косинусоидальных импульсов, как показано фиг. 7. Постоянная составляющая тока I₀ при усилении ограниченного входного гармонического сигнала, нормированная относительно пика тока I_s:

где T_a=1/ƒ_a - период гармонического сигнала;

z=V_a/V_s=I_a/I_s - уровень ограничения;

ϕ=across(1/z) - угол ограничения, характеризующий время действия ограничения.

Отсутствию ограничения соответствует ϕ=0, c₀=1/π, ток в нагрузке имеет форму гармонического сигнала и КПД усилителя определяется соотношением (1.12). Жесткому ограничению (клиппированию) соответствует ϕ=π/2, Ч₀=1/2, ток в нагрузке имеет форму меандра, ряд Фурье которого содержит нечетные гармоники частоты ƒ_a с убывающими амплитудами (Радиотехнические цепа и сигналы. Учебник для вузов / И.С. Гоноровский. - Изд. 3-е, перераб. и доп. - М.: Связь, 1977, - 608 с.):

Мощность в нагрузке равна сумме мощностей всех гармоник:

Потребляемая усилителем мощность и КПД при усилении клишированного гармонического сигнала;

Как видно, с ростом уровня ограничения входного сигнала КПД усилителя растет и в пределе ограничен только падением напряжения на активных элементах.

Ограничение является нелинейной операцией и гармонические составляющие рядов Фурье сигналов подмножества В на входе и выходе ограничителя различны. Составляющие на входе имеют частоты ƒ_k=g_kΔƒ парциальных сигналов и амплитуды y₀V_k. Составляющие на выходе имеют частоты ƒ_m=mΔƒ и амплитуды в соответствии с равенством Парсеваля;

где S_n0 - постоянная составляющая сигнала s_n(t);

S_nm - амплитуда m-й гармоники разложения в ряд Фурье сигнала s_n(t) на интервале Т.

Уровень ограничения сигналов подмножества В является функцией времени.:

Уровень ограничения, как следует из (2.2, 2.17), тем выше, чем больше пик-фактор сигнала. Потребляемая усилителем мощность и локальный КПД при усилении сигналов подмножества В:

где

Эффективность усиления в способе-прототипе характеризуется средним КПД как математического ожидания локальных КПД при усилении сигналов подмножеств А и В:

На фиг. 8 приведена зависимость η'_med=ϕ_η(y₀,X_s) для полного кода равновероятных, равномощных сигналов с двоичной модуляцией фазы в способе-прототипе (K=8). Как видно, средний КПД в способе-прототипе выше среднего КПД способа-аналога.

При усилении сигналов подмножества В мощность выходного сигнала распределена между полезными парциальными сигналами на частотах ƒ_k=g_kΔƒ и сигналами на частотах ƒ_m=mΔƒ(m≠g_k).

Мощность каждого парциального сигнала определяется соответствующим коэффициентом ряда Фурье ограниченного сигнала s_n(t):

где - относительная амплитуда k-го парциального сигнала n-й реализации выходного сигнала.

Если при усилении сигналов подмножества А мощность каждого парциального сигнала в раз больше, чем в способе-аналоге, то при усилении сигналов подмножества В мощность каждого парциального сигнала определяется величиной c_nk, которая, в свою очередь, зависит от величии y₀,X_s и реализации сигнала. Вероятность ошибки приема парциальных сигналов подмножества B в способе-прототипе будет не хуже, чем в способе-аналоге, если для любого, сигнала этого подмножества значения y₀,X_s таковы, что выполняется нестрогое равенство:

Невыполнение условия (2.22) означает, что мощность некоторых парциальных сигналов в реализации многочастотного сигнала на выходе усилителя в способе-прототипе меньше их мощности в способе-аналоге и вероятность ошибки приема таких сигналов возрастает.

На фиг. 9 приведена зависимость c_min=ϕ_c(y₀,X_s) для полного кода равновероятных, равномощных сигналов с двоичной модуляцией фазы (K=8). Как видно, условие (2,22) выполняется при определенных значениях относительного порога ограничения и коэффициента масштабирования.. Чрезмерное уменьшение относительного порога ограничения (снижение мощности P'_pek относительно мощности P_pek) приводит к невыполнению условия (2.22) ни при каком значении коэффициента масштабирования и вероятность ошибки в способе-прототипе будет хуже, чем в способе-аналоге.

Составляющие выходного сигнала на частотах ƒ_m=mΔƒ(m≠g_k). называемые внеполосным излучением, создают помехи соседним системам связи. Их мощность убывает (не обязательно монотонно) по мере удаления от полосы частот парциальных сигналов. Поэтому уровень внеполосного излучения, в основном, характеризуется мощностью сигналов в ограниченной области частот. Например, в области L из K частот, максимальная из которых на 2Δƒ меньше частоты первого парциального сигнала ƒ₁ и в области R из K частот, минимальная из которых на 2Δƒ больше частоты K-го парциального сигнала ƒ_К. Мощность каждого сигнала P_nm в этих областях пропорциональна квадрату амплитуды соответствующей гармоники разложения в ряд Фурье ограниченного сигнала s_n(t) на интервале Т и относительный уровень внеполосных излучений определяется коэффициентами ряда Фурье ограниченного сигнала s_n(t) в этих областях, частот:

Максимальный относительный уровень внеполосного излучения при усилении ограниченного сигнала s_n(f) есть наибольшая из величин w_mn,L, w_mn,R:

Усиление мощности сигналов подмножества В характеризуется диапазоном относительного уровня внеполосного излучения от w_min до w_max:

На фиг. 10 приведена зависимость w_max=ϕ_w(y₀,X_s) для полного кода равновероятных, равномощных сигналов с двоичной модуляцией фазы.

При небольших значениях коэффициента масштабирования максимальный уровень внеполосного. излучения имеет место при ограничении сигналов с максимальным пик-фактором, например, сигнала ν₀(t).

С ростом коэффициента масштабирования максимальный уровень внеполосного излучения, как это видно из графиков на фиг. 11, имеет место при ограничении сигналов с меньшими значениями пик-фактора.

На фиг. 12 приведена зависимость w_min=ϕ_{w min}(y₀,X_s) для полного кода равновероятных, равномощных сигналов с двоичной модуляцией фазы в способе-прототипе (K=8). Резко выраженный немонотонный характер w_min при изменении, коэффициента масштабирования обусловлен зависимостью (2.4) критического пик-фактора от этого коэффициента - с его ростом ограничению подвергается все большее количество сигналов.

Для некоторых систем, связи, например гидроакустических, проблема «тесноты в эфире» не актуальна и высокий уровень внеполосного излучения несущественен. Следовательно, для таких систем целесообразно получение высокого КПД усилителя ценой высокого внеполосного излучения, т.е. заданием больного значения коэффициента масштабирования. Но его увеличение ограничено условием (2.22) в результате чего КПД усилителя также ограничен, в противном случае вероятность ошибки при приеме возрастает.

Для других систем связи уровень внеполосного излучения существенен и его уменьшение в способе-прототипе, из-за зависимости критического пик-фактора от коэффициента масштабирования, сопряжено с уменьшением КПД усилителя.

Как видно, способу-прототипу свойственны ограниченные показатели по КПД усилителя и внеполосному излучению, что является его недостатком.

Раскрытие изобретения

Задача, на решение которой направлено заявляемое изобретение, заключается, в повышению показателей по КПД усилителя и внеполосному излучению.

Техническими результатами при осуществлении изобретения является повышение КПД усилителя мощности, улучшение показателей внеполосного излучения.

Указанные технические результаты достигаются тем, что в способе передачи информации многочастотными сигналами, состоящего из преобразования последовательности информационных символов в комбинацию модулирующих символов, формирования многочастотного сигнала в виде суммы ортогональных парциальных сигналов различных частот, каждый из которых модулирован по фазе соответствующим модулирующим символом, масштабирования суммарного сигнала путем его умножения на коэффициент масштабирования, ограничения масштабированного сигнала и усиления мощности, коэффициент масштабирования задают таким, что коэффициенты ряда Фурье ограниченного сигнала удовлетворяют заданным критериям качества системы связи.

Краткое описание чертежей

Прилагаемые чертежи, гистограммы и графики, составляющие часть настоящего описания, иллюстрируют сущность известных и заявляемого способов передачи информации многочастотными сигналами.

Фиг. 1 - Структура алгоритма способа-аналога, где:

1 - преобразование последовательности информационных символов b в комбинацию модулирующих символов r_nk;

2 - формирование многочастотного сигнала;

3 - усиление мощности;

ν_n(t) - сформированный сигнал;

u_n(t) - сигнал на выходе усилителя мощности.

Фиг. 2- Гистограмма пик-факторов полного кода равновероятных, равномощных сигналов с двоичной модуляцией фазы (K=8), где:

П_j - пик-фактор, П_med - средний пик-фактор ансамбля сигналов;

q_j - количество сигналов с пик-фактором П_j.

Фиг. 3 - Гистограмма локальных КПД при усилении полного кода равновероятных, равномощных сигналов с двоичной модуляцией фазы для способа-аналога (K=8, δ_U=0). где;

η_i - локальный КПД; η_med - средний КПД;

q_i - количество сигналов, при усилении которых КПД усилителя равен η_i.

Фиг. 4 - Структура алгоритма способа-прототипа, где:

1 - преобразование последовательности информационных символов b в комбинацию модулирующих символов r_nk;

2 - формирование многочастотного сигнала;

4 - масштабирование сформированного сигнала;

5 - ограничение масштабированного сигнала;

3 - усиление мощности;

y₀ - коэффициент масштабирования;

y₀ν_n(t) - масштабированный сигнал на входе ограничителя;

s_n(t) - сигнал на выходе ограничителя;

u'_n(t) - сигнал на выходе усилителя мощности,

Фиг. 5 - Сигналы на входе, выходе ограничителя, огибающая ограниченного сигнала, где:

y₀ν(t) - масштабированный сигнал та входе ограничителя;

s(t) - сигнал на выходе ограничителя;

S(t) - огибающая, ограниченного сигнала.

Фиг. 6 - Зависимость П_s=ϕ_П(y₀,X_s) для полного кода равновероятных, равномощных сигналов с двоичной модуляцией фазы в способе-прототипе (K=8), где;

П_s - критический пик-фактор, П_min - минимальный пик-фактор;

y₀ - коэффициент масштабирования;

X_s - относительный порог ограничения,

Фиг. 7 - Форма тока в активном элементе усилителя мощности, где:

1 - входной гармонический сигнал не ограничен;

2 - входной гармонический сигнал ограничен;

ƒ_a - частота входного гармонического сигнала;

I_a - амплитуда тока - входной гармонический сигнал, не ограничен;

I_s - пик тока - входной гармонический сигнал ограничен.

Фиг. 8 - Зависимость η'_med=ϕ_η(y₀,X_s) для полного кода равновероятных, равно-мощных сигналов с двоичной модуляцией фазы в способе-прототипе (K=8). где:

η'med - средний КПД;

y₀ - коэффициент масштабирования;

X_s - относительный порог ограничения,

Фиг. 9 - Зависимость c_min=ϕ_с(y₀,X_s) для полного кода равновероятных, равномощных сигналов с двоичной модуляцией фазы (K=8), где:

c_min - минимальная относительная амплитуда парциального сигнала;

y₀ - коэффициент масштабирования;

X_s - относительный порог ограничения.

Фиг. 10 - Зависимость w_max=ϕ_w(y₀,X_s) для полного кода равновероятных, равно-мощных сигналов с двоичной модуляцией фазы (K=8), где:

w_max - максимальный относительный уровень внеполосного излучения;

y₀ - коэффициент масштабирования;

X_s - относительный порог ограничения,

Фиг. 11 - Зависимость Δw_m=w_max-w_{0 max} полного кода равновероятных, равномощных сигналов с двоичной модуляцией фазы (K=8), где:

w_max - максимальный относительный уровень внеполосного излучения;

w_{0 max} - максимальный относительный уровень внеполосного излучения сигнала с максимальным пик-фактором ν₀(t);

y₀ - коэффициент масштабирования;

X_s - относительный- порог ограничения.

Фиг. 12 - Зависимость w_min=ϕ_{w min}(y₀,X_s) для полного кода равновероятных, равно-мощных сигналов с двоичной модуляцией фазы в способе-прототипе (K=8), где;

w_min - минимальный относительный уровень внеполосного излучения;

y₀ - коэффициент масштабирования;

X_s - относительный порог ограничения.

Осуществление изобретения

Формирование многочастотного сигнала ν_n(t) в системах связи на основе OFDM-технологии обычно осуществляют методом обратного дискретного преобразования Фурье модулирующих символов средствами цифровой вычислительной техники. Этими средствами также выполняют все действия, необходимые для осуществления заявляемого способа.

В заявляемом способе, коэффициент масштабирования задают таким, что коэффициенты ряда Фурье ограниченного сигнала удовлетворяют заданным критериям качества системы связи. Коэффициент масштабирования, в общем случае, определяют повторением одной и той же процедуры: сформированный сигнал ν_n(t) умножают на число больше единицы, ограничивают полученный сигнал, вычисляют коэффициенты ряда Фурье этого сигнала и проверяют их значения на соответствие заданным критериям качества. Если соответствие не достигнуто, то задают другое число и повторяют процедуру. Число, при котором достигнуто соответствие, является требуемым коэффициентом масштабирования и соответствующий ему масштабированный а ограниченный сигнал подают на усилитель мощности. Коэффициенты масштабирования определяют; непосредственно в процессе работы системы связи, или заранее, выбирая требуемый процессе работы системы связи, или непосредственно в процессе работы системы связи, для одних сигналов, для других - заранее, выбирая требуемый в процессе работы системы связи. Приводимые примеры показывают осуществление заявляемого способа для разных критериях качества системы связи. Численные значения характеристик даны для ансамбля сигналов, пик-факторы которых приведены на фиг. 2.

Критерий качества: максимум КПД усилителя

Повышение КПД усилителя в. способе-прототипе осуществляют заданием максимально возможного значения коэффициента масштабирования y₀, при котором величина c_min соответствует условию (2.22). Например, как видно из графиков на фиг. 9, при относительном пороге X_s=2,75 и коэффициенте масштабирования y₀=2,5 величина c_min соответствует требуемому условию, следовательно, вероятность ошибки приема ограниченных сигналов в способе-прототипе будет не хуже, чем в способе-аналоге.

При условном единичном уровне амплитуд всех парциальных сигналов (V=1) пиковая мощность усилителя в способе-аналоге должна составлять 32 отн. ед. Согласно соотношению (2.5), пиковая мощность усилителя в способе-прототипе может быть снижена до 15,125 отн. ед. - более чем в два раза.

В заявляемом способе используют тот же усилитель, что и в способе-прототипе и налагают условие, чтобы вероятность ошибки приема ограниченных сигналов в заявляемом способе была не-хуже, чем в способе-прототипе. Тогда коэффициент масштабирования каждого сформированного сигнала ν_n(t) определяют как решение уравнения целевой функции:

где c'_{n min} - минимальный относительный коэффициент ряда Фурье в области частот парциальных сигналов, определяют аналогично соотношению (2.22);

w'_n - относительный уровень внеполосного излучения в заявляемом способе, который определяют аналогично соотношению (2.24).

Правило (3,1) позволяет получить наибольший КПД при усилении каждого сигнала, не ухудшая вероятность ошибки при его приеме, ценой большого числа вычислений: надлежит определять и анализировать коэффициенты ряда Фурье как в области внеполосного излучения, так и в области частот парциальных сигналов.

Менее затратный в вычислительном плане коэффициент масштабирования сформированного сигнала ν_n(t) определяют как решение более простой целевой функции;

где w_{0 max} - относительный уровень внеполосного излучения в способе-прототипе при излучении сигнала ν₀(t).

Правило (3.2), не ухудшая вероятность ошибки приема ограниченных сигналов, уменьшает вычислительные затраты ценой снижения КПД относительно достижимого по правилу (3.1).

В таблице 1. характеристики способов передачи по КПД усилителя (δ₁=0).

Как видно из таблицы 1, заявляемый способ позволяет получить более высокий КПД усилителя, не ухудшая вероятность ошибки при приеме ограниченных сигналов. Характерной особенностью правила (3.2) является одинаковый уровень внеполосного излучения для всех сигналов.

Критерий качества: повышение КПД усилителя при заданном уровне внеполосного излучения

В способе-прототипе это осуществляют заданием такого значения коэффициента масштабирования y₀, при котором величина c_min соответствует условию (2.22), а относительный уровень внеполосного излучения сигнала ν₀(t) не превышает заданный.

В заявляемом способе используют тот же усилитель, что и в способе-прототипе и налагают условие, чтобы вероятность ошибки приема ограниченных сигналов в заявляемом способе была не хуже, чем в способе-прототипе. Тогда коэффициент масштабирования каждого сформированного сигнала ν_n(t) определяют как решение системы уравнений целевых функций:

Первая целевая функция правила (3,3) не требует определения коэффициентов ряда Фурье сигнала на выходе ограничителя, т.к. сигналы с пиковыми значениями огибающих, не превышающих порога ограничения, образуют не подвергающееся ограничению подмножество А':

где S_{n max} - пиковое значение огибающей сигнала на выходе ограничителя.

Внеполосное излучение при усилении сигналов подмножества А' в заявляемом способе отсутствует.

Условие принадлежности сигнала к подмножеству А', выраженное через его пик-фактор:

В заявляемом способе критический пик-фактор П'_s не зависит от коэффициента масштабирования и всегда больше критического пик-фактора в способе-прототипе:

Следовательно, все сигналы подмножества А являются частью подмножества А' и чем выше требованиях к внеполосному излучению, тем сильнее выполняются соотношения y_n>y₀≈1, поэтому мощность этих сигналов и локальные КПД при их усилении в заявляемом способе выше, чем в способе-прототипе;

Сигналы с пиковыми значениями огибающих, не меньше порога ограничения, образуют подмножество В' и для этих сигналов коэффициент масштабирования определяют как решение второй целевой функция правила (4.1), которая позволяет получить уровень внеполосного излучения не выше заданного, не ухудшая вероятность ошибки при их приеме. В заявляемом способе максимальный коэффициент масштабирования для сигналов подмножества В' равен коэффициенту масштабирования y₀ в способе-прототипе, а минимальный коэффициент масштабирования равен единице (при наличии в ансамбле сигналов с пик-фактором, равного критическому значению П'_s). Следовательно, локальный КПД при усилении сигналов с максимальным пик-фактором одинаков в заявляемом способе и способе-прототипе, а для других сигналов подмножества В' локальные КПД в заявляемом способе ниже, чем в способе-прототипе, Сигналы подмножества В' являются лишь частью подмножества В. поэтому низкие значения локальных КПД составляют малую долю в среднем значении КПД.

Сигналы, пик-факторы которых находятся между значениями П_s и П'_s, в способе-прототипе подвергаются ограничению и создают внеполосное излучение, в заявляемом способе эти сигналы не подвергаются ограничению и не создают внеполосного излучения. В заявляемом способе коэффициенты масштабирования этих сигналов больше единицы, но меньше коэффициента масштабирования в способе-прототипе y₀. Следовательно, локальные КПД при их усилении находятся между значениями локальных КПД для подмножеств В' и А и близки к локальным. КПД при усилении этих сигналов в способе-прототипе. В итоге, среднее значение КПД в заявляемом способе тем выше среднего значения КПД в способе-прототипе чем выше требования по внеполосному излучению предъявляются к системе связи.

Менее затратный в вычислительном плане коэффициент масштабирования сформированного сигнала ν_n(t) определяют как решение более простой системы целевых функций, не требующих определения