Встраиваемый в классический компьютер электронный блок и используемый в нём способ, основанный на квантовой процедуре счета

Встраиваемый в классический компьютер электронный блок и используемый в нём способ, основанный на квантовой процедуре счета

Иллюстрации

Показать все

Реферат

Область техники, к которой относится изобретение

Изобретение относится к квантовым технологиям, направленным на создание квантового компьютера с целью решения таких неразрешимых на сегодняшний день задач, как быстрая обработка и анализ очень большого банка данных.

Изобретение относится к приоритетным направлениям развития науки и технологий «Нанотехнологии и наноматериалы» и «Технологии создания электронной компонентной базы» [Алфавитно-предметный указатель к Международной патентной классификации по приоритетным направлениям развития науки и технологий / Ю.Г. Смирнов, Е.В. Скиданова, С.А. Краснов. - М.: ПАТЕНТ, 2008. - С. 18, с. 94], так как в настоящее время обработка данных, описываемых матрицами с большим числом элементов, занимает многие часы и даже многие сутки.

Уровень техники

Проблема создания устройства, основанного на квантовой процедуре счета, заключается в следующем.

Сравнительно быстро после пионерских статей Р. Фейнмана [Feynman R.P., Simulating Physics with Computers // International Journal of Theoretical Physics, v. 21, No. 6/7, p.467-488 (1982); Feynman R.P., Quantum Mechanical Computers // Foundations of Physics, v. 16, No. 6, p.507-531 (1986). 1, 2] относительно необходимости и возможности создания квантового компьютера, а также книги Манина Ю.П., в которой проведено детальное обсуждение проблемы существования невычислимых функций и связанных с ней алгоритмически неразрешимых задач [Манин Ю.И. Вычислимое и невычислимое. - М.: Сов. радио, 1980. - 128 с. 3], была выполнена целая серия исследований теоретического характера по указанной тематике. Результатом таких исследований стали многочисленные публикации, включая обзорные работы и монографии [см., например, обзорные статьи Килин С.Я. Квантовая информация // Успехи физических наук, т.169, №5, с. 507-526 (1999); Jones J.A., NMR Quantum Computation, in Quantum Entanglement and Information Processing, D.Esteve, J.-M.Raimond, and J.Dalibard (Eds.), Elsevier Science (2004); Валиев K.A. Квантовые компьютеры и квантовые вычисления // Успехи физических наук, т.175, №1, с. 3-39 (2005); Voronov V.K., NMR and the Problem of Quantum Computer Creation: New Outlook, in: S. Shannon (ed.), Trends in Quantum Computing Research, NOVA Publishers: New York, 2006, p.73-90; 4-7] и приведенную там литературу).

Теоретические успехи в решении проблемы квантовых компьютеров основывались на идеи использования физических процессов, которые обеспечивали бы выполнение логических операций, аналогичных таковым в классических компьютерах. При этом предполагалось, что использование специфики квантовых объектов позволит улучшить технику расчета, но не изменит принципиально его суть. Казалось, что в результате были найдены необходимые условия, выполнение которых и должно вскоре обеспечить успешную экспериментальную реализацию идеи Р. Фейнмана. Тем более, что этапная работа Шора [Shor P.W., Algorithms for Computation: Discreta Logarithms and Factoring, Proceeding of the 35th Annual Symp. on the Foundation of Computer Science, Los Alamitos, С A, USA, 1994, p.124-134; 8] обозначила круг реальных задач, решение которых возможно только с использованием квантовых компьютеров.

Уверенность в скором создании квантовых компьютеров в немалой степени была обусловлена и тем, что уже в 1998 году появились работы, в которых сообщалось о реализации элементарного квантового алгоритма с помощью двух q-битов на основе явления ядерного магнитного резонанса (ЯМР). В одном случае это были спины ядер атомов водорода (протоны), а в другом - водорода и углерода [Jones J.A., Mosca М.J., Implementation of a quantum algorithm on a nuclear magnetic resonance quantum computer // Chem. Phys., v.109, №5, p.1648-1653 (1998); Chuang I.L., Gershenfeld N., Kubinec M., Experimental Implementation of Fast Quantum Searching // Phys. Rev. Lett., v.18, №15, p.3408-3411 (1998); 9, 10].

В упомянутых двух работах была проиллюстрирована сама возможность создать алгоритм на основе идеи квантовых вычислений и только. Для решения же реальных задач он не предназначался.

Большинство выполненных к настоящему времени исследований основываются на поиске подходящих индивидуальных квантовых объектов. В указанном направлении проделана значительная работа. В связи с этим можно упомянуть публикации [Harty Т.Р., Allcock D.T.C, Balance C.J., Guidoni L., Janacek H.A., Linke N.M., Stacey D.N., and Lucas D.M., High-Fidelity Preparation, Gates, Memory, and Readout of a Trapped-Ion Quantum Bit // Physical Review Letters, v. 113, 220501 (2014); Рябцев И.И., Бетеров И.И., Третьяков Д.Б., Энтин В.М., Якшина Е.А. Спектроскопия холодных ридберговских атомов рубидия для применения в квантовой информации // Успехи физических наук, т.186, №2, с. 206-220 (2016); Gaebler J.P., Tan T.R., Lin Y., Wan Y., Bowler R., Keith A.C., Glancy S., Coakley K., Knill E., Leibfried D., and Wineland D.J., High-Fidelity Universal Gate Set for 9Be+ Ion Qubits // arXiv: 1604.00032v1; Алдошин С.М., Зенчук A.M., Фельдман Э.Б., Юрищев М.А. На пути к созданию материалов для квантовых компьютеров // Успехи химии, т.81, №2, с. 91-104 (2012); 15. Zhaokai Li, Hui Zhou, Chenyong Ju, Hongwei Chen, Wenqiang Zheng, Dawei Lu, Xing Rong, Changkui Duan, Xinhua Peng, and Jiangfeng Du, Experimen-tal Realization of Compressed Quantum Simulation of 32-spin Ising Chain // Physical Review Letters, Vol.112. p p.220501-220505 (2014); Briegel H.J., Browne D.E., W., Raussendorf R. and Van den Nest M, Meas-urement-based quantum computation // Nature Physics, vol. 5, pp. 19-26 (2009). 11-16], а также приведенные там ссылки.

Как результат проделанной работы - теоретическая проработка деталей проблемы создания квантового компьютера. Более того, ряд исследователей полагают, что готовы довести ее до такой стадии, когда эта проблема станет по своей сути технической.

Сформулированы основные критерии, которым должны удовлетворять устройства, способные выполнять процедуру счета на основе квантовых вычислений [DiVincenzo D.P., The Physical Implementation of Quantum Compution // Fortscher. Phys., vol. 48, pp.771-783 (2000). 17].

Что касается экспериментальных результатов, то можно только констатировать достижение определенных успехов в реализации идеи Р. Фейнмана. Однако возможность осуществления реальных квантовых вычислений на практике предстоит еще доказать.

Из уровня техники не выявлено аналогов заявляемых устройства и способа.

Раскрытие сущности изобретения

Изобретение направлено на решение задачи по созданию квантового компьютера с целью решения неразрешимых на сегодняшний день задач. Изобретением принципиально решается проблема декогеренции кубитов, так как предлагаемые к использованию нанотриггеры и квантовые точки создаются в условиях контроля их строения и внутримолекулярной динамики, а потому могут использоваться в качестве элементов электронного устройства сколь угодно долго при определенных условиях, причем число кубитов в предлагаемом устройстве при необходимости может быть увеличено.

Технический результат заявляемого изобретения заключается в реализации возможности квантовых вычислений, поскольку эта техническая проблема решается изобретением впервые. Другими словами, технический результат заключается в реализации назначения заявляемых устройства и способа.

Технический результат изобретения достигается тем, что устройство для квантовых вычислений согласно изобретению содержит блок, включающий по меньшей мере 10¹⁰ нанотриггеров, выполняющих роль кубитов - битов квантового счета, созданных на основе нанолент графена и управляемых элементом, который представляет собой действующую по принципу самоорганизации квантовую точку с двумя существенно различными по магнитным свойствам состояниями, созданную на основе вещества, для молекул которого характерна внутримолекулярная перегруппировка, при этом из нанотриггеров сформированы обладающие свойством обратимости логические блоки или вентили по три триггера в каждом блоке или вентиле для выполнения логических операций, лежащих в основе квантовых вычислений.

Технический результат изобретения достигается тем, что система нанотриггеров сопоставлена возможным перепутанным состояниям квантовой системы, обеспечивающим большой математический информационный ресурс, и что в качестве элементов устройства использованы нанотриггеры и квантовые точки, созданные в условиях контроля их строения и внутримолекулярной динамики. В качестве основы материала для создания управляющего элемента - квантовой точки использовано соединение, в котором внутримолекулярные процессы приводят к заселению 3d - орбиталей металла вследствие валентной таутомерии. Устройство для квантовых вычислений представляет собой встраиваемый в цифровой компьютер дополнительный электронный блок, обеспечивающий возможность реализации вычислительного процесса в соответствии с требованиями положений квантовой физики.

Технический результат изобретения достигается тем, что способ квантовых вычислений согласно изобретению предусматривает использование при процедуре счета числа изначально необходимых значимых цифр и задание числа кубитов в соответствии с решаемой задачей и получаемому банку данных путем увеличения числа логических блоков или вентилей.

Включение в блок устройства по меньшей мере 10¹⁰ нанотриггеров, выполняющих роль кубитов - битов квантового счета, созданных на основе нанолент графена, позволяет на практике реализовать выдвинутую более тридцати лет идею создания ЭВМ, работа которых контролируется законами микромира (квантовой физики). При этом элементная база таких ЭВМ формируется с использованием нанотехнологий и наноматериалов.

Создание элемента, который представляет собой действующую по принципу самоорганизации квантовую точку с двумя существенно различными по магнитным свойствам состояниями, на основе вещества, для молекул которого характерна внутримолекулярная перегруппировка, позволяет обеспечить нахождение нанотригггеров, выполняющих роль кубитов, в двух состояниях. Это одно из необходимых условий, выполнение которых обеспечивает возможность формировать вентили на основе нанотриггеров.

Кубит должен иметь два состояния (находиться в двух состояниях), чтобы смог выполнять планируемую для него роль. Обычно это можно сделать, как-то на него воздействуя, например, помещением его в магнитное поле. В случае соединений, которые в силу процесса самоорганизации (через валентную таутомеризацию) могут находиться в двух состояниях, существенно отличающихся магнитными свойствами, их (эти состояния) можно использовать для кодирования нуля и единицы, а следовательно, для организации процедуры счета.

Обеспечение соответствующего функционирования кубитов не является самоцелью. Главное в создании квантового компьютера связано с возможностью использования квантовых состояний массива кубитов в организации процедуры счета. Но если это так, то с учетом существующих трудностей в подборе кубитов логично а priory создавать систему из необходимого количества квантовых объектов (квантовых точек или островков), которые будут соответствовать перепутанным квантовым состояниям. Именно такие состояния и являются основой алгоритма, предложенного Шором. Уместно поэтому здесь говорить о визуализации перепутанных состояний, называя их состояниями Шора. Квантовые состояния алгоритма Шора являются по своей сути виртуальными по отношению к макромиру, т.е. к тем реальным условиям, в которых должен работать квантовый компьютер. Этот факт, как известно, является следствием фундаментального принципа квантовой механики, согласно которому невозможно получить все амплитуды вероятностей C_i в разложении суперпозиционного состояния |ψ〉. Доступными для этого являются только квадратичные формы вида ΣC_iC_jR_ij, соответствующие измерению на уровне макромира среднего значения некоторой физической величины, которой сопоставляется оператор . Проблема состоит в том, чтобы иметь возможность визуализовать все возможные состояния ϕ_i для их включения в процедуру счета.

Из вышеизложенного вытекает первая и, возможно, самая главная необходимость на пути решения проблемы создания квантового компьютера - визуализация или материализация упомянутых выше состояний, не подверженных процессам декогеренции [Voronov V.K. Revisiting the Possible Creation of the Quantum Information Unit - A Necessary Element of Quantum Computation Procedure // Transactions on Networks and Communications, V. 3 №1. - P. 79-84 (2015). 18]. Только после этого можно говорить о соответствии первого этапа работы квантового компьютера этапу внесения (записи) цифровой информации в регистр классического компьютера. Причем необходимо иметь в виду, что визуализация не должна изменить реальность, т.е. обеспечить квантовый характер состояний q-битов.

Ниже рассмотрим блок-схему электронного квантового устройства на основе a priory визуализованных перепутанных состояний кубитов.

На данном этапе квантовый компьютер в истинном смысле - это встраиваемый в уже существующие современные компьютеры дополнительный блок, вычислительный процесс в котором осуществляется в соответствии с требованиями положений квантовой физики. Ясно, что в таком варианте отпадает необходимость во включении в квантовый процессор, выполняющий непосредственно математические операции, сопутствующих периферийных устройств.

Как уже отмечалось выше, подбор системы кубитов и обеспечение их должной работы в состоянии перепутанности не является самоцелью. Главное в создании квантового компьютера связано, в конечном счете, с возможностью использования квантовых состояний массива кубитов в организации процедуры счета.

В плане реализации процедуры квантового счета самым естественным представляется процесс, при котором каждой материализованной (визуализированной) ячейке Шора сопоставляется элемент электронной схемы. Затем такие элементы объединяются в соответствующую схему, способную выполнять процесс счета. Причем и элементы ее, и она сама в целом должны функционировать на основе положений квантовой физики. Являясь действительно квантовой системой по своей сути, такое устройство выполняет реальные процедуры счета по схеме классического компьютера, но на уровне микромира.

Хорошо известно, что центральным устройством современного (классического) компьютера является процессор, который фактически и обеспечивает его (компьютера) работу, т.е. процедуру счета и его управление. Работа процессора организуется на основе электронных схем, основным элементом которых является триггер, который может выполнять роль хранителя разряда двоичного кода. Переходя под воздействием внешнего сигнала попеременно в одно из двух устойчивых состояний, одно из которых соответствует единице, а другое - нулю, триггер обеспечивает реализацию в конечном счете процесса счета на основе двоичной системы исчисления. Совокупность триггеров, объединенных определенным образом, позволяет создавать необходимые для успешной работы процессора блоки, называемые регистрами.

На основе вышеизложенного можно положить, что триггер создается на основе графеновых лент шириной 10 нм [Сорокин П.Б., Чернозатонский Л.А. Полупроводниковые наноструктуры на основе графена // Успехи физических наук, т.183, №2, с. 113-132 (2013). 19]. В этом случае триггер будет занимать площадь, равную примерно 5⋅10^-14 м². Следовательно, на одном квадратном сантиметре может разместиться порядка 10¹⁰ триггеров. Это те самые квантовые объекты, которые должны выполнять роль кубитов - битов квантового счета. Принципиальным моментом в использовании графенового триггера для выполнения элементарной процедуры счета является необходимость обеспечения его работы по законам микромира, т.е. законам квантовой физики. Это можно сделать на основе принципа самоорганизации. Здесь необходимо следующее пояснение [20].

Пусть зависимость амплитуды отклонения от исходного состояния x определяется выражением вида

где a и b - постоянные положительные коэффициенты, отражающие природу процесса, описываемого формулой (1);

х - переменная величина, характеризующая протекание процесса, в нашем случае - процесса таутомеризации комплекса кобальта (см. далее);

n≥2.

Если x<<1, то bxⁿ<<ax, поэтому

Таким образом, в случае (2) растет линейно с ростом x. Если же величина x окажется сравнимой с единицей, то членом bxⁿ пренебрегать уже нельзя, т.е. для описания поведения системы необходимо использовать исходное уравнение (1). Следовательно, рост отклонения функции за счет члена ax начнет испытывать нелинейное ограничение в силу вычитания величины bxⁿ. При некоторых значениях x функция вновь будет близка к нулю и все начинается сначала. Система будет как бы автоматически себя регулировать, так как ее свойства зависят от текущего состояния (в данном случае - от величины x). Отсюда логично заключить, что, изменяя каким-либо образом данную молекулярную систему, можно в принципе добиться необходимых значений для соответствующего параметра (или параметров).

Среди фундаментальных задач центральное место занимают такие внутримолекулярные перегруппировки, в процессе которых неспаренные электроны с лигандов делокализуются на ион металла (например, кобальта) с изменением валентности последнего. Такие перегруппировки принято называть валентной таутомерией. Применительно к соединениям первой переходной группы указанные внутримолекулярные процессы приводят к заселению 3d-орбиталей металла неспаренными электронами. Проведенные исследования показали, что магнитные свойства соединений могут изменяться драматическим образом в процессе перехода молекул из состояния А в состояние Б и обратно. Это было проиллюстрировано, в частности, при изучении спиновых фазовых переходов в наноразмерных структурах переходных металлов на примере комплекса Co(SQ)₂(2-2'-dipyridine) [21, 22].

Опуская детали фазового перехода, отраженного в приведенной схеме, следует иметь в виду, что вещество, молекулы которого находятся в состоянии А, оказывается диамагнитным, а в состоянии Б - парамагнитным.

Для кодирования чисел (например, нуля и единицы) можно использовать два состояния парамагнитной молекулы, реализуемых вследствие фазовых расслоений. Так как такие состояния соответствуют конкретным структурам парамагнитной молекулы, они могут существовать при определенных условиях сколь угодно долго. Миграция электрона между различными состояниями (спиновыми неоднородностями) - это тот самый процесс самоорганизации, соответствующий условию (1), который обеспечит постоянную во времени реализацию двух существенно различных по магнитным свойствам состояний.

Здесь необходимо следующее пояснение. Традиционно в качестве квантового бита информации (q-бита) рассматривается квантовая система с двумя возможными базовыми состояниями - |0〉 и |1〉. Такая двухуровневая система позволяет создать соответствующую элементную базу, включающую логические блоки или вентили для выполнения соответствующих логических операций, которые и должны составлять основу счета в квантовом компьютере. Имеются в виду, прежде всего, операции «НЕ», «ИЛИ», «И». Так два q-бита, на каждом из которых находится по одному неспаренному электрону, позволяют выполнять логическую операцию «НЕ». Соответствующим образом можно организовать и другие логические операции, реализуемые, в конечном счете, в ЭВМ. Для этого в качестве исходных универсальных логических блоков достаточно иметь такие устройства, которые позволяли бы многократно выполнять соответствующие логические операции. Другими словами, эти устройства (логические вентили) должны обладать свойством обратимости. Таковым, в частности, является трехбитовый вентиль Тоффоли (см., например, [Валиев К.А. Квантовые компьютеры и квантовые вычисления // Успехи физических наук, т.175, №1, с.3-39 (2005). 6]).

Новые совокупности существенных признаков, характеризующих техническую сущность заявляемых устройства и используемого в нем способа доказывают новизну заявляемых объектов.

Из уровня техники известно использование квантовых точек для создания элементов электронных устройств. Однако из уровня техники не известно использование квантовых точек для управления работой нанотриггера. Из уровня техники также не известно создание квантовых точек на основе вещества, для молекул которого характерна внутримолекулярная перегруппировка, в частности, валентная таутомерия с двумя существенно различными по магнитным свойствам состояниями. Следовательно, заявляемое устройство соответствует условию патентоспособности «изобретательский уровень». Из уровня техники не известны существенные признаки заявляемого способа, следовательно, заявляемый способ соответствует изобретательскому уровню.

Краткое описание чертежей

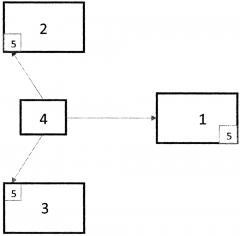
Изобретение поясняется чертежом, где приведена блок-схема квантового вентиля, иллюстрирующая возможную блок-схему каждого из упомянутых выше 10⁸ вентилей.

Осуществление изобретения

Цифрами 1, 2, 3 обозначены нанотриггеры (возможный материал их изготовления - графен);

4 - коммуникационный блок, который управляет работой триггеров, обеспечивая при необходимости согласование их состояний. Такой блок может быть сделан на основе фемтосекундного лазера [Voronov V.K., Physical problems of quantum calculation: A novel approach // Journal of Physical Science and Application, v. 2, №4, p. 115-122 (2012). 23];

5 - включаемая в электронную схему нанотриггера квантовая точка, которая за счет процесса самоорганизации переводит нанотриггеры из одного состояния в другое.

Можно следующим образом представить процедуру проведения квантового счета. Будем исходить из того, что основу его составляет блок площадью один квадратный сантиметр, на котором можно разместить, как было показано выше, порядка 10¹⁰ нанотриггеров. Далее, созданный на основе лент графена каждый нанотриггер управляется элементом, который представляет собой квантовую точку с двумя состояниями. Она создается на основе вещества, для молекул (кластеров) которого характерна внутримолекулярная перегруппировка, в частности валентная таутомерия. Например, на основе комплекса кобальта. В целом такая система является квантовой по своей сути. Следовательно, на основе такого элемента можно создать устройство, работа которого полностью определяется законами микромира (квантовой физикой), в том числе изменение состояния нанотриггера как следствие перехода квантовой точки из одного состояния в другое. Три нанотриггера объединяются в группу, которая должна выполнять роль универсального вентиля. Работа такого вентиля может выполнять логическую операцию ИЛИ-НЕ. Это означает, что состояние одного из трех кубитов (кубит состояния цели или результата счета) меняется тогда и только тогда, когда два других кубита (биты источников, символизирующих исходную информацию, необходимую для реализации процедуры квантового счета) имеют строго конкретное значение. В соответствии с этим организуется такая коммутация между тремя нанотриггерами, которая обеспечивает реализацию логической операции ИЛИ-НЕ, то есть один из нанотриггеров должен выполнять роль кубита состояния цели или результата счета. Учитывая, что в отсутствие такой коммутации каждый нанотриггер может функционировать независимо от двух других нанотриггеров, организация их согласованной работы при современном состоянии электроники является чисто технической задачей.

Исходя из вышеизложенного, процедуру счета можно организовать, положив, что исходное состояние группы из трех нанотриггеров являет также собой и результат счета. Таким образом, реализуется условие обратимости универсального вентиля. Констатирование того факта, что исходное состояние суть также и результат счета означает, что это состояние можно сопоставить единице. Нарушение такого состояния означает нуль. Таким образом, счет в двоичной системе в принципе оказывается организованным. Если исходить из того, что на одном квадратном сантиметре располагается порядка 10¹⁰ нанотриггеров, то на указанной площадке можно создать порядка 10⁹ вентилей, участвующих автономно в процедуре квантового счета. Реально их может быть меньше, так как организация работающего электронного устройства предполагает использование и других (помимо) нанотриггеров элементов. Будем поэтому исходить из того, что упомянутых выше вентилей можно создать порядка 10⁸, которые размещены на блоке площадью, равной не одному, а десяти квадратным сантиметров.

Чтобы проиллюстрировать потенциальные возможности квантового компьютера, уместно обратиться к хорошо известной схеме работы классического компьютера, которую принято представлять как последовательность трех операций: 1) запись исходных данных в регистр ЭВМ; 2) проведение вычислений; 3) вывод результата. Первому этапу классического компьютера принято сопоставлять этап приготовления начального состояния квантового компьютера. Это означает создание устройства, на подобие регистра классической ЭВМ, содержащего достаточно большое число квантовых объектов, находящихся в перепутанных состояниях [Килин СЛ. Квантовая информация // Успехи физических наук, т.169, №5, с. 507-526 (1999). 4; Валиев К.А. Квантовые компьютеры и квантовые вычисления // Успехи физических наук, т.175, №1, с. 3-39 (2005). 6].

Согласно законам квантовой физики, если система состоит из n двухуровневых q-битов (qubit), то ее состояние в общем случае представляет суперпозицию 2ⁿ базовых состояний |ψ_i〉=|i₁i₂…i_n〉, i_k=0; 1, т.е. (здесь используются общепринятые обозначения) [Валиев К.А. Квантовые компьютеры и квантовые вычисления // Успехи физических наук, т.175, №1, с. 3-39 (2005). 6]:

Здесь |ψ〉 волновая функция, описывающая состояние всей квантовой системы, содержащей n квантовых объектов,

|ψ_i〉 - волновая функция, описывающая состояние i-го квантового объекта, i изменяется от 1 до 2^n-1,

α_i - коэффициент, с которым волновая функция i-го квантового объекта входит в состав волновой функции системы.

Если ограничиться относительно небольшим n=10² квантовых частиц (q-битов), можно получить достаточно большой

математический информационный ресурс квантового компьютера. Именно отсюда вытекают основные преимущества квантового компьютера. В самом деле, в процессе записи числа, содержащего, скажем, n цифр, именно столько ячеек и будет занято из общего количества, равного 10³⁰. Остальные (не занятые) ячейки можно использовать для проведения параллельных вычислений.

Здесь необходимо подчеркнуть, что эти ячейки - не какие-то конкретные элементы схем и не магнитные участки (домены), на которые можно записать необходимую информацию. Речь идет о собственных значениях оператора физической величины, характеризующей данную систему q-битов, которые, согласно законам квантовой механики, можно определять с той или иной степенью вероятности. В определенном смысле речь идет о большом наборе виртуальных по своей доступности ячеек, использование которых далеко не очевидно. Это одна из принципиальных проблем. Далее, после того, как в эти ячейки будет занесена информация (например, цифровая), ими необходимо как-то управлять с целью выполнения вычислительных операций. И, наконец, необходимо найти способ вывести результат после проведения процедуры счета. Из этого можно сделать заключение о тех трудностях принципиального характера, которые предстоит преодолеть на пути создания квантового компьютера. Для оценки наименьшей скорости счета положим, что в каждом состоянии квантовая точка находится порядка 10^-2 секунды, то есть достаточно долго. Цикл счета при двоичной системе предполагает реализацию двух состояний, на что потребуется 2⋅10^-2 секунды для каждого из 10⁸ вентилей. Если исходить из автономности их работа, то можно заключить, что описываемое здесь возможное устройство должно выполнять 5⋅10⁹ счетных операций в секунду. Нетрудно заключить, что это величина может быть заметно увеличена за счет уменьшения времени нахождения нанотриггера в каждом из состояний. Далее, расчетную единицу площади подложки (на чертеже не приведена) можно увеличить до квадрата со стороной 10 см, то есть площадью сто квадратных сантиметров. Уже такими двумя способами, предполагающими выполнение довольно мягких условий, число операций в секунду может быть доведено по порядку до 10¹², то есть до одной гигаоперации в секунду. Дальнейшая обработка считанной таким образом информации может осуществляться хорошо разработанным интерфейсом современных классических ЭВМ.

Здесь уместно следующее пояснение. Человечество давно придумало универсальный способ - системы единиц для количественного счета. Фактически и ЭВМ используют этот подход, для чего применяется наиболее универсальная двоичная система. Особенности традиционных систем счета - ограниченное число в них конкретных чисел, которые при определенном периодическом применении позволяют проводить любые математические операции счета. Принципиальная особенность предлагаемой в данной заявке процедуры - фактически неограниченное число изначально значимых цифр, которые можно использовать в процессе счета.

Создание заявляемого нами устройства предполагает использование нанотехнологий, а также наноматериалов. В этих условиях важным моментом является обоснование комплектования классических современных ЭВМ достаточно дорогостоящим (специфическим) дополнительным блоком. Назначение такого блока, как уже отмечалось выше, - возможность проведения оперативного (достаточно быстрого) анализа большого массива (банка) данных. Наличие таких массивов обусловлено необходимостью решения конкретных задач из самых различных разделов науки, техники, других разделов человеческой деятельности. В связи с этим можно утверждать о наличии многих типовых по методам решения задач. Зная условие таких задач, можно задавать число кубитов m, которое определяет число возможных перепутанных состояний (2^m), позволяющих в конечном счете получать необходимый банк данных. В свою очередь, такая информация является основой для создания встраиваемого блока с необходимым количеством нанотриггеров, управляемых квантовыми точками, действующими по принципу самоорганизации с двумя существенно различными по магнитным свойствам состояниями и созданными на основе вещества, для молекул которого характерна внутримолекулярная перегруппировка. Предлагаемый блок квантового счета может подключаться такими же способами, как это делается по отношению к дополнительным устройствам современных ЭВМ.

Литература

1. Feynman R.P., Simulating Physics with Computers // International Journal of Theoretical Physics, v. 21, No. 6/7, p.467-488 (1982).

2. Feynman R.P., Quantum Mechanical Computers // Foundations of Physics, v. 16, No. 6, p.507-531(1986).

3. Манин Ю.И. Вычислимое и невычислимое. - М.: Сов. радио, 1980. - 128 с.

4. Килин С.Я. Квантовая информация // Успехи физических наук, т.169, №5, с. 507-526 (1999).

5. Jones J.А., NMR Quantum Computation, in Quantum Entanglement and Information Processing, D.Esteve, J.-M. Raimond, and J. Dalibard (Eds.), Elsevier Science (2004).

6. Валиев K.A. Квантовые компьютеры и квантовые вычисления // Успехи физических наук, т.175, №1, с. 3-39 (2005).

7. Voronov V.K., NMR and the Problem of Quantum Computer Creation: New Outlook, in: S. Shannon (ed.), Trends in Quantum Computing Research, NOVA Publishers: New York, 2006, p.73-90.

8. Shor P.W., Algorithms for Computation: Discreta Logarithms and Factoring, Proceeding of the 35^th Annual Symp. on the Foundation of Computer Science, Los Alamitos, CA, USA, 1994, p.124-134.

9. Jones J.A., Mosca M.J., Implementation of a quantum algorithm on a nuclear magnetic resonance quantum computer // Chem. Phys., v. 109, №5, p.1648-1653 (1998).

10. Chuang I.L., Gershenfeld N., Kubinec M., Experimental Implementation of Fast Quantum Searching // Phys. Rev. Lett, v.18, №15, p.3408-3411(1998).

11. Harty T.P., Allcock D.T.C, Balance C.J., Guidoni L., Janacek H.A., Linke N.M., Stacey D.N., and Lucas D.M., // High-Fidelity Preparation, Gates, Memory, and Readout of a Trapped-Ion Quantum Bit // Physical Review Letters, v. 113, 220501 (2014).

12. Рябцев И.И., Бетеров И.И., Третьяков Д.Б., Энтин В.М., Якшина Е.А. Спектроскопия холодных ридберговских атомов рубидия для применения в квантовой информации // Успехи физических наук, т.186, №2, с. 206-220 (2016).

13. Gaebler J.P., Tan T.R., Lin Y., Wan Y., Bowler R., Keith A.C., Glancy S., Coakley K., Knill E., Leibnied D., and Wineland D.J., High-Fidelity Universal Gate Set for ⁹Be⁺ Ion Qubits // arXiv: 1604.00032v1.

14. Алдошин С.М., Зенчук A.M., Фельдман Э.Б., Юрищев М.А. На пути к созданию материалов для квантовых компьютеров // Успехи химии, т.81, №2, с. 91-04 (2012).

15. Zhaokai Li, Hui Zhou, Chenyong Ju, Hongwei Chen, Wenqiang Zheng, Dawei Lu, Xing Rong, Changkui Duan, Xinhua Peng, nd Jiangfeng Du, Experimen-tal Realization of Compressed Quantum Simulation of 32-spin Ising Chain // Physical Review Letters, Vol.112. pp. 220501-220505 (2014).

16. Briegel H.J., Browne D.E., W., Raussendorf R. and Van den Nest M, Meas-urement-based quantum computation // Nature Physics, vol. 5, pp.19-26 (2009).

17. DiVincenzo D.P., The Physical Implementation of Quantum Compution // Fortscher. Phys., vol. 48, pp.771-783 (2000).

18. Voronov V.K. Revisiting the Possible Creation of the Quantum Information Unit - A Necessary Element of Quantum Computation Procedure // Transactions on Networks and Communications, V. 3 №1. - P. 79-84 (2015).

19. Сорокин П.Б., Чернозатонский Л.А. Полупроводниковые наноструктуры на основе графена // Успехи физических наук, т.183, №2, с. 113-132 (2013).

20. Voronov V.K., Possible schemes of calculation modeling in a quantum computer // Natural Science, v. 2, №8, p.923-927 (2010).

21. Sato О., Tao J., Zhang Y.-Z. Control of Magnetic Properties through External Stimule // Angew. Chem. Int. Ed., v. 46, p.2152-2171 (2007).

22. Мищенко A.C. Спиновые фазовые переходы в наноразмерных материалах переходных металлов, индуцированные сильным магнитным полем: дис… канд. физ.-мат. н. 01.04.11: защищена 16.02.06: утв. 10.05.06. М.: МГУ, 2006.134 с.

23. Voronov V.K., Physical problems of quantum calculation: A novel approach // Journal of Physical Science and Application, v. 2, №4, p.115-122 (2012).

1. Устройство для квантовых вычислений, включающее блок, содержащий по меньшей мере 10¹⁰ нанотриггеров, выполняющих роль кубитов - битов квантового счета, созданных на основе нанолент графена и управляемых элементом, который представляет собой действующую по принципу самоорганизации квантовую точку с двумя существенно различными по магнитным свойствам состояниями, созданную на основе вещества, для молекул которого характерна внутримолекулярная перегруппировка, при этом из нанотриггеров сформированы обладающие свойством обратимости логические блоки или вентили по три нанотриггера в каждом блоке или вентиле для выполнения логических операций, лежащих в основе квантовых вычислений.

2. Устройство по п. 1, отличающееся тем, что система нанотриггеров сопоставлена возможным перепутанным состояниям квантовой системы, обеспечивающим большой математический информационный ресурс.

3. Устройство по п. 1, отличающееся тем, что в качестве элементов устройства использованы нанотриггеры и квантовые точки, созданные в условиях контроля их строения и внутримолекулярной динамики.

4. Устройство по п. 1, отличающееся тем, что в качестве основы материала для создания управляющего элемента - квантовой точки использовано соединение, в котором внутримолекулярные процессы приводят к заселению 3d-орбиталей металла вследствие валентной таутомерии.

5. Устройство по п. 1, отличающееся тем, что представляет собой встраиваемый в цифровой компьютер дополнительный электронный блок, обеспечивающий возможность реализации вычислительного процесса в соответствии с требованиями положений квантовой физики.