Способ установления битовой синхронизации псевдослучайных последовательностей с использованием принципов декодирования

Способ установления битовой синхронизации псевдослучайных последовательностей с использованием принципов декодирования

Иллюстрации

Показать все

Реферат

Изобретение относится к технике связи и может быть использовано в системах передачи данных для установления синхронизации псевдослучайных последовательностей (ПСП) большой длины по малому фрагменту этой последовательности (пилотному), принятому из канала связи и возможно содержащему некоторое количество ошибочных символов.

Аналогом данного изобретения является способ, описанный в статье [Калугин Е. Поиск и синхронизация псевдослучайных последовательностей. Современная электроника №9, 2009. С. 30-32]. Процесс установления синхронизации заключается в определении величины сдвига принимаемой последовательности относительно опорной. Опорной последовательностью является та же последовательность, вырабатываемая на приемной стороне и сдвинутая на некоторое количество разрядов. После суммирования входной и опорной последовательностей по закону «исключающее ИЛИ» результат поступает на детекторы определенных специфичных для данной последовательности комбинаций. При срабатывании детектора логическое устройство, по данным счетчика, определяет на каком такте появилась комбинация и на какое количество разрядов необходимо сдвинуть опорную последовательность для достижения полного совпадения опорной и принимаемой последовательностей.

Существенный недостаток такого способа заключается в том, что при наличии хотя бы одной ошибки в принимаемой пилотной последовательности установить точную синхронизацию невозможно, т.к. в этом случае будет может будет установлена ложная синхронизация

Наиболее близким к заявленному техническому решению является способ установления синхронизации псевдослучайных последовательностей, описанный в патенте РФ №2542900 от 27.02.2015 и принятый за прототип. Способ установления синхронизации псевдослучайных последовательностей состоит в том, что по принятой пилотной последовательности длины n, являющейся отрезком псевдослучайной последовательности длины N, причем n<<N, устанавливается синхронизация между всей принимаемой псевдослучайной последовательностью и вырабатываемой на приемной стороне псевдослучайной последовательностью, при этом из принятой пилотной последовательности выбирается фрагмент длиной m, на основе которого генерируется последовательность длиной n, которая сравнивается с принятой пилотной последовательностью путем подсчета количества несовпадений, и в случае количества несовпадений менее заданного порога r синхронизация считается установленной, при большем количестве несовпадений из пилотной последовательности выбирается другой фрагмент длиной m, после чего вновь осуществляется проверка на установление синхронизации, состоящая в генерировании последовательности длиной n, сравнении ее с принятой пилотной последовательностью, подсчета количества несовпадений и сравнении полученного количества несовпадений с пороговым значением r, если после перебора всех фрагментов длиной m из принятой пилотной последовательности синхронизация не установлена, то из принятой пилотной последовательности осуществляется перебор всех возможных фрагментов длиной m с последовательным инвертированием по одному биту всех бит в выбранном фрагменте и последующей проверкой на установление синхронизации после каждой процедуры инвертирования, если после перебора всех фрагментов с последовательным инвертированием по одному биту всех бит в каждом выбранном фрагменте синхронизация не установлена, то из принятой пилотной последовательности осуществляется перебор всех возможных фрагментов длиной m с последовательным инвертированием по два бита всех бит в выбранном фрагменте и последующей проверкой на установление синхронизации после каждой процедуры инвертирования.

Недостатком прототипа является большой объем вычислений при последовательной пробной инверсии одного или двух бит, генерации каждый раз пилотной последовательности длины n и сравнении ее с принятой пилотной последовательностью.

Целью изобретения является уменьшение времени на установление битовой синхронизации между принимаемой псевдослучайной последовательностью и последовательностью, вырабатываемой в приемнике, при наличии ошибок в принимаемой последовательности, а также уменьшение объема вычислений.

Поставленная цель достигается тем, что способ установления битовой синхронизации псевдослучайных последовательностей с использованием принципов декодирования заключается в том, что по принятой пилотной последовательности длины n, являющейся отрезком псевдослучайной последовательности длины N, причем n<<N, устанавливают синхронизацию между всей принимаемой псевдослучайной последовательностью и вырабатываемой на приемной стороне псевдослучайной последовательностью, при этом из принятой пилотной последовательности выбирают фрагмент длиной m, на основе которого генерируют последовательность длиной n, которую сравнивают с принятой пилотной последовательностью путем подсчета количества несовпадений, при этом принятую пилотную последовательность длиной n умножают на проверочную матрицу H, полученную следующим образом: H=[-G_p^T|E], где E - единичная матрица размерностью (n-m)×(n-m), G_p - матрица, полученная на основе порождающего полинома ПСП, являющаяся фрагментом порождающей матрицы в систематическом виде G=[E|G_p], где Е - единичная матрица размерностью m×m, в результате чего получают вектор синдрома, на основе которого корректируют ошибки во фрагменте пилотной последовательности длиной m, затем на основе откорректированного фрагмента пилотной последовательности длиной m генерируют последовательность длиной n и сравнивают ее с принятой пилотной последовательностью путем подсчета количества несовпадений, после чего сравнивают полученное количество несовпадений с пороговым значением r и принимают решение об установлении синхронизации, если полученное количество несовпадений меньше порога r, или не установлении синхронизации, если полученное количество несовпадений больше порога r, при этом пороговое значение r выбирают исходя из того, что r<t, где t - исправляющая способность кода, а также допустимого значения вероятности ложной синхронизации.

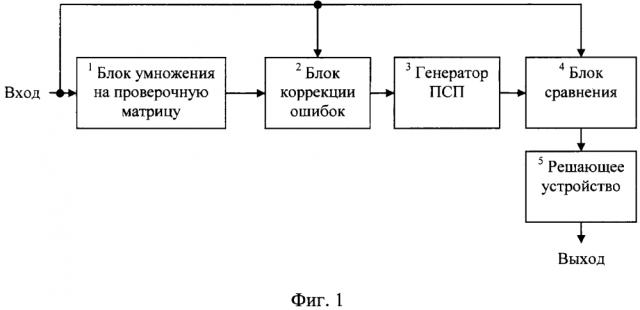
На фиг. 1 представлена структурная схема способа установления битовой синхронизации псевдослучайных последовательностей с использованием принципов декодирования. Она содержит:

1 - блок умножения на проверочную матрицу;

2 - блок коррекции ошибок;

3 - генератор ПСП;

4 - блок сравнения;

5 - решающее устройство.

Работа способа осуществляется следующим образом.

На входе принимают пилотную последовательность длины n, которая является отрезком ПСП длины N, причем n<<N. При этом в принятой пилотной последовательности могут содержаться ошибки. Для коррекции ошибок в описываемом способе предлагается воспользоваться аппаратом помехоустойчивого кодирования. Как известно из [Алексеев А.И., Шереметьев А.Г., Тузов Г.И., Глазов Б.И. Теория и применения псевдослучайных сигналов. М.: Наука, 1969, с. 47-84], имея любой фрагмент ПСП длиной m бит можно сгенерировать как всю ПСП длиной N=2^m-1, так и некоторый ее участок длиной n<<N. Будем считать, что m<n, и в n битах присутствует фрагмент длиной m. Это можно представить в матричной форме следующим образом:

β_1,n=β_1,m⋅G,

где β_1,m - вектор строка, фрагмент ПСП длиной m бит; β_1,n - вектор строка, участок ПСП длиной n бит; G - порождающая матрица размерностью m×n в систематическом виде, т.е.:

G=[E|G_p],

где Е - единичная матрица размерностью m×m т, G_p - матрица, полученная на основе порождающего полинома ПСП, причем первый ее столбец есть порождающий полином: G_p,1=[α₁ α₂ … α_m]^Т (α_k - элементы полинома), а последующие столбцы G_p,k=[g_k,1 g_k,2 … g_k,m]^T образуются из элементов g_k,j=g_k-1,j⋅g_1,j+g_k-1,j+1 для j=1…m-1 и g_k,m=g_k-1,m⋅g_1,m.

На основе порождающей матрицы можно получить проверочную матрицу, как описано, например, в [Кларк Дж., Кейн Дж. Кодирование с исправлением ошибок в системах цифровой связи. М.: Радио и связь, 1987, с. 61] следующим образом:

H=[-G_p^T|E],

где Е - единичная матрица размерностью (n-m)×(n-m).

Таким образом, поступившую пилотную последовательность длины n умножают на проверочную матрицу Н, получая вектор синдрома, однозначно указывающий ошибочные биты при условии, что количество ошибочных бит меньше исправляющей способности кода.

На основе полученного вектора синдрома в принятой пилотной последовательности корректируют ошибки (если они имеются) в фрагменте длиной m. Исправленный фрагмент длиной m передают на генератор ПСП, получают последовательность длиной n бит, которую затем сравнивают с пилотной последовательностью путем подсчета количества несовпадений.

Затем полученное количество несовпадений сравнивают в решающем устройстве с пороговым значением r и принимают решение об установлении (полученное количество несовпадений меньше порога) или не установлении (полученное количество несовпадений больше порога) синхронизации.

Пороговое значение r выбирают заранее исходя из следующего:

1) r<t, где t - исправляющая способность кода;

2) допустимое значение вероятности ложной синхронизации.

Техническим результатом является уменьшение времени на установление битовой синхронизации между принимаемой псевдослучайной последовательностью и последовательностью, вырабатываемой в приемнике, при наличии ошибок в принимаемой последовательности, достигаемое за счет уменьшения объема вычислений.

Так в прототипе требуется поочередно генерировать пилотную последовательность длины n и сравнивать ее с принятой пилотной последовательностью раз. Здесь - число сочетаний из m по 2. В предлагаемом способе требуется лишь один раз генерировать пилотную последовательность длины n и сравнить ее с принятой пилотной последовательностью.

Способ установления битовой синхронизации псевдослучайных последовательностей с использованием принципов декодирования, заключающийся в том, что по принятой пилотной последовательности длины n, являющейся отрезком псевдослучайной последовательности длины N, причем n<<N, устанавливают синхронизацию между всей принимаемой псевдослучайной последовательностью и вырабатываемой на приемной стороне псевдослучайной последовательностью, при этом из принятой пилотной последовательности выбирают фрагмент длиной m, на основе которого генерируют последовательность длиной n, которую сравнивают с принятой пилотной последовательностью путем подсчета количества несовпадений, отличающийся тем, что принятую пилотную последовательность длиной n умножают на проверочную матрицу H, полученную следующим образом: H=[-G_p^T|Е], где Е - единичная матрица размерностью (n-m)×(n-m), G_p - матрица, полученная на основе порождающего полинома ПСП, являющаяся фрагментом порождающей матрицы в систематическом виде G=[E|G_p], где Е - единичная матрица размерностью m×m, в результате чего получают вектор синдрома, на основе которого корректируют ошибки во фрагменте пилотной последовательности длиной m, затем на основе откорректированного фрагмента пилотной последовательности длиной m генерируют последовательность длиной n и сравнивают ее с принятой пилотной последовательностью путем подсчета количества несовпадений, после чего сравнивают полученное количество несовпадений с пороговым значением r и принимают решение об установлении синхронизации, если полученное количество несовпадений меньше порога r, или не установлении синхронизации, если полученное количество несовпадений больше порога r, при этом пороговое значение r выбирают исходя из того, что r<t, где t - исправляющая способность кода, а также допустимого значения вероятности ложной синхронизации.