Способ определения механических свойств породы пласта-коллектора

Способ определения механических свойств породы пласта-коллектора

Иллюстрации

Показать все

Реферат

Изобретение относится к области исследования механических, тепловых и петрофизических свойств горных пород и предназначено для оценки свойств пласта-коллектора и интенсификации добычи.

При проектировании работ по добыче углеводородов с применением гидроразрыва пласта и/или тепловых методов увеличения нефтеотдачи часто требуется знания различных свойств горных пород при атмосферных термобарических условиях и повышенных температурах (например, механических - предел прочности на сжатие, модуль Юнга, коэффициент Пуассона; петрофизических - плотность, пористость, проницаемость, минеральный состав и проч.; тепловых - теплопроводности, объемной теплоемкости и проч.). Знания этих свойств могут быть ключевыми при проектировании и оценке рисков таких процессов, как бурение (в том числе горизонтальных скважин), цементация, гидроразрыв пласта, стимуляция добычи нефти тепловыми методами и др.

Создание моделей физических (например, механических или транспортных) свойств пласта часто производится с помощью коммерчески доступных программных пакетов (например, Techlog, Petrel-Visage, CMG-STARS) в одномерном и трехмерном приближении. Для корректной работы программных пакетов, моделирующих вмещающие, механические или транспортные свойства пласта, необходимо в качестве входных данных использовать сведения о соответствующих свойствах пород и насыщающих флюидов пласта, которые получают из лабораторных, каротажных либо иных экспериментальных исследований.

Известен способ оценки качества пласта и качества заканчивания в скважинах, пробуренных в нетрадиционных (сланцевых) коллекторах нефти и газа, описанный в патенте США №8967249. В указанном способе упругие свойства горных пород определяются двумя независимыми путями: прямыми измерениями V_p и V_s скоростей и с использованием модели. Однако прямые измерения проводятся на единичных, подготовленных образцах/частицах породы, что снижает репрезентативность выборки и приводит к низкому разрешению данных о механических/упругих свойствах по разрезу/интервалу/скважине. Кроме того, в способе не предусмотрена оценка степени анизотропии, которая важна для оценки качества пласта-коллектора и/или качества заканчивания скважины. Надежность результатов использования модели без информации о структурных и микротекстурных факторах, структуре пустотного пространства породы (включая, без ограничений, степень сцементированности минеральных зерен скелета, пористость, особенности контактов между зернами минерального скелета) крайне низка. Необходимость очистки частиц шлама до измерений приводит к увеличению временных затрат, к тому же экстракция углеводородов из образцов нефтематеринских пород может быть выполнена лишь частично. К недостаткам способа также относят отсутствие поправок за пластовые термобарические условия. Известно, что при извлечении кернов из скважины на поверхность происходят изменения физических свойств образцов породы (расхождение между измеренными свойствами в атмосферных условиях и реальными свойствами образцов породы может быть значительным).

Указанные недостатки снижают надежность результатов определения упругих свойств, что затрудняет / делает неэффективной оценку качества пласта-коллектора и качества заканчивания скважины.

В патенте США №5285692 описаны методы измерения физических параметров, в том числе упругих свойств низко проницаемых пород в пластовых условиях. Способ подразумевает измерение на образцах породы (или в скважине) скоростей распространения ультразвуковых колебаний наряду с использованием корреляций. Однако каротажные данные могут отсутствовать, использование корреляций подразумевает наличие чрезвычайно информативной/объемной базы данных (из-за разнообразия пород и насыщающих их флюидов), а прямые измерения скоростей распространения ультразвуковых колебаний проводятся на единичных, подготовленных образцах/частицах породы, что снижает репрезентативность выборки и приводит к низкому разрешению данных о механических/упругих свойствах по разрезу/интервалу/скважине. Не предусмотрена оценка степени анизотропии, которая важна для оценки качества пласта-коллектора и/или качества заканчивания скважины.

Технический результат, достигаемый при реализации изобретения, заключается в повышении эффективности и качества оценки свойств пласта за счет обеспечения возможности расчета значений неизвестных (или известных не полностью) механических и/или вмещающих свойств резервуара.

Полученные величины механических и/или вмещающих свойств резервуара могут быть использованы для выбора продуктивных интервалов пласта, оценки пригодности интервалов скважины для вскрытия и применения методов увеличения нефтеотдачи (гидроразрыв пласта, кислотная обработка и т.п.).

В соответствии с предлагаемым способом осуществляют отбор по меньшей мере одного образца породы пласта-коллектора, на отобранном образце породы определяют плотность, пористость и компонентный состав породы и на основе полученных значений создают петрофизическую модель породы пласта-коллектора. Измеряют теплопроводность образца. Используя созданную петрофизическую модель пласта-коллектора, рассчитывают теплопроводность образца породы. Сравнивают измеренную и рассчитанную теплопроводности образца породы и в случае совпадения значений измеренной и рассчитанной теплопроводностей определяют механические свойства породы, используя созданную петрофизическую модель пласта-коллектора. В случае наличия расхождения между значениями измеренной и рассчитанной тепловодности, по меньшей мере один раз осуществляют адаптацию созданной петрофизической модели пласта-коллектора путем изменения параметров модели. Используют адаптированную петрофизическую модель для расчета теплопроводности образца породы и сравнивают измеренную и рассчитанную теплопроводности до обеспечения совпадения значений измеренной и рассчитанной теплопроводностей. При совпадении значений измеренной и рассчитанной теплопроводностей определяют механические свойства породы, используя адаптированную петрофизическую модель пласта-коллектора.

В соответствии с одним из вариантов осуществления изобретения механические свойства породы пласта-коллектора представляют собой скорости распространения продольной акустической волны и поперечной акустической волны через образец.

В соответствии с одним из вариантов осуществления изобретения отобранные образцы перед проведением измерений очищают.

В соответствии с еще одним вариантом осуществления изобретения отобранный образец по меньшей мере один раз насыщают флюидом с известными свойствами, отличающимися от свойств воздуха не менее чем в десять раз, измеряют теплопроводность насыщенного образца и дополнительно сравнивают измереную теплопроводность насыщенного образца и рассчитанную теплопроводность.

Адаптация созданной петрофизической модели пласта-коллектора может быть осуществлена путем изменения параметров, характеризующих структуру пустотного пространства породы пласта-коллектора или путем изменения параметров, характеризующих структурно-текстурные факторы, или путем изменения параметров, характеризующих минерально-компонентный состав породы пласта-коллектора.

Образцы пласта-коллектора могут представлять собой образцы полноразмерного керна или его фрагментов, образцы стандартного керна, частицы бурового и/или обвального шлама, а также брикеты, состоящие из частиц, скрепленные между собой связующим материалом с известными тепловыми и механическими свойствами.

В соответствии с одним из вариантов осуществления изобретения петрофизическая модель породы пласта-коллектора может быть создана на основе теории эффективных сред, при этом неоднородности породы представляют в виде эллипсоидов вращения с различными аспектными отношениями главных осей.

В соответствии с еще одним вариантом осуществления изобретения дополнительно измеряют скорости прохождения продольной акустической волны и/или поперечной акустической волны через образец, на основе созданной петрофизической модели пласта-коллектора рассчитывают скорости соответствующей акустической волны, сравнивают измеренные и рассчитанные скорости акустической волны и дополнительно обеспечивают совпадение измеренной и рассчитанной скоростей акустической волны.

В соответствии с еще одним вариантом осуществления изобретения дополнительно измеряют зависимость теплопроводности образца от времени, температуры и/или давления. На основе созданной петрофизической модели пласта-коллектора рассчитывают соответствующую зависимость теплопроводности образца от времени, температуры и/или давления, сравнивают измеренную и рассчитанную зависимости и дополнительно обеспечивают совпадение измеренной и рассчитанной зависимостей теплопроводности образца от времени, температуры и/или давления.

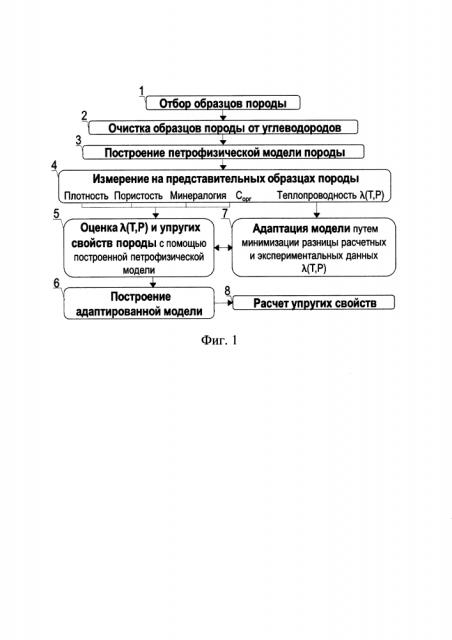
Изобретение поясняется чертежами, где на фиг. 1 представлена блок-схема одного из вариантов реализации изобретения; на фиг. 2 приведено сравнение расчета скорости продольной акустической волны брикета, рассчитанной методом теории эффективных сред, с измеренной скоростью продольной акустической волны; на фиг. 3 показано сравнение скорости поперечной акустической волны брикета, рассчитанной методом теории эффективных сред, с измеренной скоростью поперечной акустической волны; на фиг. 4 показано сравнение расчетных и экспериментальных данных по теплопроводности, скоростям продольных и поперечных акустических волн для сухих и водонасыщенных образцов песчаника Бентхаймер; на фиг. 5 показаны экспериментальные данные зависимости теплопроводности от приложенной нагрузки при одноосном сжатии; на фиг. 6 изображено. как изменяется внутреннее поровое пространство образца под приложенным давлением с помощью двух гистограмм функции плотности распределения формы (аспектного отношения) элементов порового пространства; на фиг. 7 представлены результаты сравнения измеренных и расчетных зависимостей V_p и V_s от напряжения приложенной осевой нагрузки.

На фиг. 1 приведен пример осуществления способа, включающий несколько этапов, где С_орг - содержание органического углерода, λ(Т,Р) - теплопроводность, измеренная в диапазоне температур Т и давлений Р в пределах от лабораторных до пластовых условий.

На этапе 1 осуществляют отбор по меньшей мере одного образца породы пласта-коллектора. Образцы породы могут представлять собой полноразмерный керн или его фрагменты, образцы стандартного керна, частицы бурового и/или обвального шлама, брикеты, состоящие из частиц, скрепленных между собой связующим материалом с известными тепловыми и механическими свойствами. Профильные исследования полноразмерного керна позволяют набрать статистику и провести сравнение значения промоделированных механических свойств с результатами акустического каротажа (I. Bayuk, Yu. Popov, A. Parshin A New Powerful Tool for Interpreting and Predicting in Reservoir Geophysics: Theoretical Modeling As Applied to Laboratory Measurements of Thermal Properties, International Symposium of the Society of Core Analysts held in Austin, Texas, USA, September 18th - 21st, 2011; Popov Y.A., Mikhaltseva I.V., Chekhonin E.M., Popov E.Y., Romushkevich R.A., Kalmykov G.A. and Latypov I.D., Application of Effective Medium Theory to Reconstruction of Elasticity Tensor of Bentheimer Sandstone, 17th science and applied research conference on oil and gas geological exploration and development, 7-10 September 2015 Gelendzhik, Russia Geomodel 2015).

Исследования образцов стандартного керна являются предпочтительными - для Российской Федерации это цилиндры диаметром 30 мм и высотой 25…60 мм - поскольку имеется значительное количество опробованных стандартных методов для определения тепловых и механических свойств, плотности и пористости таких образцов, а также выпущено значительное количество стандартного оборудования для проведения таких измерений (ГОСТ 21153.2-84 Породы горные. Методы определения предела прочности при одноосном сжатии).

Частицы обвального шлама могут быть исследованы аналогично образцам стандартного керна и полноразмерного керна в случае, если их линейные размеры достаточны для определения теплопроводности выбранным экспериментатором методом.

Частицы бурового шлама после очистки от бурового раствора и сушки исследуют в виде суспензии с водным раствором соли; брикета, сформированного прессованием со связующим (например, мелкозернистый парафин); таблетки, сформированной склеиванием шлама каким-либо полимером (например, двухкомпонентная эпоксидная смола).

На этапе 2 может быть произведена предварительная очистка образца от углеводородов стандартными методами (см., например, API. Recommended Practices for Core Analysis. Recommended Practice 40, Second edition, February 1998. SECTION 3. Core Screening and Core Preparation. 3-6. PP. 3-5. http://w3.energistics.org/RP40/rp40.pdf).

На этапе 3 на отобранном образце породы определяют стандартными методами (патент США №8967249) плотность, пористость и компонентный состав породы. Также проводят измерения теплопроводности образца. Измерения теплопроводности могут быть осуществлены, например, методом оптического сканирования (см., например, Попов Ю.А. Теоретические модели для определения тепловых свойств горных пород на основе подвижных источников тепловой энергии, 1983, Известия вузов, Геология и разведка, №9, с. 97-103), либо методом линейного источника (ASTM D5334 - 08 Standard Test Method for Determination of Thermal Conductivity of Soil and Soft Rock by Thermal Needle Probe Procedure) и т.п.

Затем на основе полученных значений плотности, пористости и компонентного состава породы создают петрофизическую модель породы пласта-коллектора и, используя созданную петрофизическую модель пласта-коллектора, рассчитывают теплопроводность образца породы (этап 4).

Петрофизическая модель пласта-коллектора может включать в себя данные о минералогическом составе горной породы, текстурных и структурных особенностей порового пространства и скелета и открытой пористости, которые учитываются в моделях, построенных с помощью теории эффективных сред. В простейшем случае модель может быть сведена к моделям слоистых сред, где свойства исследуемой породы определяются в результате усреднения среднеарифметического по Фойгту и среднегеометрического по Ройссу ; также может быть использована эмпирическая зависимость измеренных свойств со свойствами отдельных его компонент среднелогарифмическое усреднение по Лихтенеккеру и более сложные варианты свойств минералогических составляющих и заполняющего поры флюида.

На этапе 5 сравнивают значения измеренной теплопроводности с рассчитанным по петрофизической модели и осуществляют адаптацию модели (в простейшем случае коррекцией минералогического состава либо выбором альтернативного варианта усреднения свойств при сохранении состава, в более сложных случаях - коррекцией текстурно-структурных параметров модели).

На этапе 6 используют адаптированную модель для расчета механических свойств горной породы (этап 7), опираясь на знания о механических свойствах минералогических компонент скелета и заполняющего поры флюида.

В дополнение к измерению тепловых свойств могут быть измерены механические свойства некоторой доли образцов, например, скорости распространения продольной и поперечной акустической волны, так как дополнительные входные данные позволяют повысить точность моделирования механических свойств.

В соответствии с еще одним вариантом осуществления изобретения образец по меньшей мере один раз насыщают флюидом с известными тепловыми и механическими свойствами, отличающимися по отношению к воздуху не менее чем в десять раз и проводят дополнительные измерения теплопроводности на насыщенном образце породы. Это позволяет увеличить число неизвестных параметров модели и характеризовать сложные типы коллекторов.

Далее приведен пример реализации способа определения механических свойств породы пласта-коллектора путем создания петрофизической модели материала пласта по результатам измерений теплопроводности прессованных брикетов и скоростей распространения продольной и поперечной ультразвуковой волны, адаптации этой модели и вычисления скоростей продольной и поперечной волны исходной породы. Брикеты изготовлены из мелкозернистого парафина и частиц этих материалов, как-то: песчаник Бентхаймер, белый мрамор, низкопористый песчаник,

Сначала производят отбор по меньшей мере одного образца породы пласта-коллектора. В данном примере брикеты изготавливают из раздробленных и просеянных на сите с размером ячейки 1 мм осколков горных пород, смешанных с парафиновой пудрой Hoenscht (плотность частиц парафина 1 г/см³) в вибрационной шаровой мельнице Retsch ММ400. Массовые доли компонент составили 4:1 (твердый материал: парафин). Брикеты прессовались в ручном прессе Retsch РР25 при нагрузке 25 тонн. Диаметр брикетов составил 32 мм, высота - 6…9 мм.

Затем определяют физические свойства образцов и измеряют теплопроводность. Теплопроводность брикетов измеряют, например, методом оптического сканирования, скорости распространения продольной и поперечной ультразвуковой волны (V_p и V_s, соответственно) - методом сквозного прозвучивания при частоте 2,5 МГц при комнатных условиях. Пористость брикета определяют по известным минеральной плотности твердого материала, из которого изготовлены осколки твердой фазы (определенной, например, методом гидростатического взвешивания), известной плотности связующего парафина и массовых долей навески из которой изготовлен брикет. Теплопроводность чистого парафина определяют методом оптического сканирования на нескольких брикетов, прессованных без включения твердой фазы.

Физические свойства полученных брикетов с известным компонентным составом представлены в Таблице 1.

Для определения скоростей распространения продольной и поперечной волн в твердой фазе брикета по результатам измерений теплопроводности брикета и скоростей составляют модель брикета посредством теории эффективных сред, как описано ниже.

Для решения поставленной задачи на основе полученных плотности, пористости и компонентного состава создают петрофизическую модель породы пласта-коллектора методом теории эффективных сред. Теория эффективных сред позволяет связать эффективные свойства брикета с параметрами, описывающими особенности его структуры. В качестве таких параметров, помимо объемного содержания, физических свойств компонент изготавливаемого брикета, могут выступать также форма отдельных зерен или элементов порового пространства брикетов.

Описание параметров, наиболее качественно сближающих математическую модель среды с реальной средой, позволяет связать различные эффективные свойства брикета посредством формулы, связывающей транспортные и упругие свойства брикета.

Эффективный тензор упругости реконструируют с использованием метода теории эффективных сред в обобщенном сингулярном приближении (см. Баюк И.О. Основные принципы математического моделирования макроскопических физических свойств коллекторов углеводородов. Технологии сейсморазведки, №4, 2013, с. 5-18), согласно которому транспортные свойства связаны с упругими свойствами породы через параметры, описывающие ее структуру:

где X^* - это тензор теплопроводности или упругости для тепловой или упругой модели породы соответственно, g - вторая производная тензорной функции Грина уравнения равновесия, зависящая от формы трещин и пор и свойств тела сравнения; X^c - соответствующий тензор так называемого тела сравнения, которое выбирается в зависимости от структуры среды; I - единичный тензор. Здесь, треугольные скобки обозначают усреднение по объему образца.

Математическую модель брикетов можно определить в результате комплексного визуального и экспериментального анализа имеющихся образцов. Для брикетов, например, можно установить наличие воздушных прослоек, связанных с условиями изготовления данных брикетов. После определения особенностей структуры брикетов следует провести построение модели в две стадии:

На первой стадии свойства известных компонент минерального состава и парафина усредняют с помощью формулы (2) с использованием метода самосогласования, т.е. вместо X^c подставляют X^*. Форму зерен минералов устанавливают в результате анализа шлифов, либо микрофотограмм частиц шлама, для некоторых песчаников ее представляют сферичной. Затем рассчитывают эффективные свойства этой среды. Эту среду называют промежуточной.

На следующей стадии в промежуточную среду вводят воздушные прослойки. Посредством формулы (2) с использованием того же метода самосогласования рассчитывают эффективные свойства (тепловые и упругие) брикета.

Затем полученные данные сравнивают с экспериментальными. Решая задачу оптимизации невязки рассчитанных значений и экспериментальных, определяют неизвестные параметры. Так, для брикетов неизвестны два значения - это объем воздушных прослоек и их форма.

В дальнейшем найденные неизвестные значения используют для данного типа исследуемой породы. Постулируют, что одному типу породы соответствует единственное значение неизвестных параметров.

Построенную модель используют для расчета продольных и поперечных акустических скоростей изучаемых пород, а также расчета динамических модулей упругости (модуль Юнга, модуль объемного сжатия и т.д.) с использованием стандартных формул пересчета.

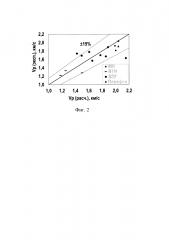
На фиг. 2 показано сравнение расчета скорости продольной акустической волны брикета методом теории эффективных сред с измеренной скоростью, а на фиг. 3 - сравнение расчета скорости поперечной акустической волны брикета методом теории эффективных сред с измеренной скоростью. На фиг. 2 и фиг. 3 использованы следующие обозначения: MR - образцы, сделанные из белого мрамора, BTN - образцов Бентхаймер, SSX - низкопористого песчаника. Сокращения «эксп.» - означают экспериментальные данные, «расч.» - расчетные данные, полученные с помощью построенной модели.

Рассмотрим другой пример создания, калибровки и применения петрофизической модели по измерениям теплопроводности образцов стандартного керна для моделирования механических свойств верхнемелового (К2) песчаника Бентхаймер. Данный песчаник хорошо изучен и используется в качестве модельной горной породы при проведении различных лабораторных исследований, в силу стабильного минералогического состава (>90% кварца), емкостных (23-25%) и фильтрационных (2-4 Д) свойств. В представленном примере исследование проводилось на 20 образцах длиной 50 мм и диаметром 30 мм в сухом и в водонасыщенном (раствором NaCl с концентрацией 15 г/л) состояниях. Тепловые свойства воды отличаются от тепловых свойств воздуха более чем в десять раз (теплопроводность воздуха составляет 0,024 Вт/(м⋅К), а теплопроводность воды 0,60 Вт/(м⋅К)).

Теплопроводность образцов измеряли методом оптического сканирования. Скорости распространения продольной и поперечной ультразвуковой волны (V_p и V_s, соответственно) - методом сквозного прозвучивания при частоте 250 кГц при комнатных условиях. Вариации измеренной теплопроводности и V_p не превышали 5% для каждого образца и, в дальнейшем, они считались изотропными.

Для расчета эффективных свойств породы используется формула (2). Форму элементов порового пространства для данного песчаника Бентхаймер описывают аспектным отношением (отношение полуосей эллипсоида), подчиняющимся двухпараметрическому бета-распределению для элементов порового пространства:

где ρ(s) - плотность вероятности бета-распределения аспектного отношения s, Г - гамма функция, α, β - параметры бета-распределения. Выбор тела сравнения для данного песчаника Бентхаймер производится с помощью метода с параметром связанности элементов порового пространства, при котором в качестве тела сравнения выбирают линейную комбинацию

где X^mat, X^ƒlu - соответствующий тензор теплопроводности или упругости для минеральной матрицы и флюида, f - параметр связанности в пределах от 0 до 1 (граничные значения соответствуют значениям эффективных свойств согласно верхней и нижней границам Хашина-Штрикмана).

По результатам структурного анализа строят модель породы, представляющую собой среду, сложенную окатанными зернами кварца (преимущественно), и межзерновым пространством в виде конечных элементов разной формы. Благодаря изотропии свойств в модели среды отсутствуют выделенные направления как минеральных зерен, так и элементов порового пространства, при этом уравнение (2) упрощается, и для описания тензора упругости используются лишь два независимых параметра, а для теплопроводности - один.

Применение метода с параметром связанности элементов порового пространства - ко всей совокупности экспериментальных данных позволяет решить задачу с приемлемой точностью. Отклонение между расчетными и измеренными данными для всех образцов (Фиг. 4) составило не более 2,5%, 12% и 15% для теплопроводности, V_p и V_s соответственно в сухом и водонасыщенном состоянии.

Рассмотрим еще один пример, в котором дополнительно измеряют зависимость теплопроводности образца от времени, температуры и/или давления. На основе созданной петрофизической модели пласта-коллектора рассчитывают соответствующую зависимость теплопроводности образца от времени, температуры и/или давления, сравнивают измеренную и рассчитанную зависимости и дополнительно обеспечивают совпадение измеренной и рассчитанной зависимостей теплопроводности образца от времени, температуры и/или давления.

Теплопроводность измеряют для двух цилиндрических ∅50-мм образцах песчаника Бентхаймер методом линейного источника, в зависимости от величины приложенной осевой нагрузки (Фиг. 5). Нагрузку повышают до величины 20 МПа, обеспечивающей упругую деформацию образца (ARMA-16-128. Yalaev, T.R. Bayuk I.О., Tarelko N.F., Abashkin V.V. Connection of Elastic and Thermal Properties of Bentheimer Sandstone Using Effective Medium Theory (Rock Physics). Proceedings of American Rock Mechanics Association Conference, Houston, 26-29 of July, 2016).

В качестве опорной модели используют модель, разработанную для 20 образцов песчаника Бентхаймер при комнатных условиях, описанная в примере выше. Делаются следующие предположения: при напряжении осевой нагрузки до 20 МПа изменение пористости незначительно (менее 0.5%), а свойства минеральных компонент, составляющих образец, не изменяются. Для различных давлений рассчитывают неизвестные параметры структуры по полученным экспериментальным данным из решения оптимизационной задачи. Путем построения гистограммы функции плотности распределения для разных напряжений осевой нагрузки оценивают изменение структуры порового пространства образца. К примеру, из (Фиг. 6) видно, что с приложением осевой нагрузки пустоты с высоким аспектным отношением (трещины) частично закрываются.

Найденные параметры структуры используют для расчета зависимости V_p и V_s от приложенной нагрузки. На (Фиг. 7) представлены результаты сравнения измеренных и теоретических зависимостей V_p и V_s от напряжения приложенной осевой нагрузки.

1. Способ определения механических свойств породы пласта-коллектора, в соответствии с которым:

- осуществляют отбор по меньшей мере одного образца породы пласта-коллектора,

- на отобранном образце породы определяют плотность, пористость и компонентный состав породы,

- измеряют теплопроводность образца породы,

- на основе полученных значений плотности, пористости и компонентного состава породы создают петрофизическую модель породы пласта-коллектора,

- используя созданную петрофизическую модель пласта-коллектора, рассчитывают теплопроводность образца породы,

- сравнивают измеренную и рассчитанную теплопроводности образца породы,

- в случае совпадения значений измеренной и рассчитанной теплопроводностей определяют механические свойства породы, используя созданную петрофизическую модель пласта-коллектора,

- в случае наличия расхождения между значениями измеренной и рассчитанной тепловодности по меньшей мере один раз осуществляют адаптацию созданной петрофизической модели пласта-коллектора путем изменения параметров модели, используют адаптированную петрофизическую модель для расчета теплопроводности образца породы и сравнивают измеренную и рассчитанную теплопроводности до обеспечения совпадения значений измеренной и рассчитанной тепловодностей,

- при совпадении значений измеренной и рассчитанной теплопроводностей определяют механические свойства породы, используя адаптированную петрофизическую модель пласта-коллектора.

2. Способ по п. 1, в соответствии с которым механические свойства породы пласта-коллектора представляют собой скорости прохождения продольной и поперечной волны через материал образца.

3. Способ по п. 1, в соответствии с которым отобранные образцы перед проведением измерений очищают.

4. Способ по п. 1, в соответствии с которым адаптацию созданной петрофизической модели пласта-коллектора осуществляют путем изменения параметров, характеризующих структуру пустотного пространства породы пласта-коллектора.

5. Способ по п. 1, в соответствии с которым адаптацию созданной петрофизической модели пласта-коллектора осуществляют путем изменения параметров, характеризующих структурно-текстурные факторы.

6. Способ по п. 1, в соответствии с которым адаптацию созданной петрофизической модели пласта-коллектора осуществляют путем изменения параметров, характеризующих минерально-компонентный состав породы пласта-коллектора.

7. Способ по п. 1, в соответствии с которым образцы пласта-коллектора представляют собой образцы полноразмерного керна или его фрагментов.

8. Способ по п. 1, в соответствии с которым образцы пласта-коллектора представляют собой образцы стандартного керна.

9. Способ по п. 1, в соответствии с которым образцы пласта-коллектора представляют собой частицы бурового и/или обвального шлама.

10. Способ по п. 1, в соответствии с которым образцы пласта-коллектора представляют собой частицы, скрепленные между собой связующим материалом с известными тепловыми и механическими свойствами.

11. Способ по п. 1, в соответствии с которым петрофизическую модель породы пласта-коллектора создают на основе теории эффективных сред и неоднородности породы представляют в виде эллипсоидов вращения с различными аспектными отношениями главных осей.

12. Способ по п. 1, в соответствии с которым измеряют по меньшей мере одну дополнительную механическую характеристику образца, на основе созданной петрофизической модели пласта-коллектора рассчитывают соответствующую механическую характеристику образца, сравнивают измеренную и рассчитанную механические характеристики образца и дополнительно обеспечивают совпадение измеренной и рассчитанной механических характеристик образца.

13. Способ по п. 12, в соответствии с которым дополнительная механическая характеристика образца представляет собой скорость прохождения продольной и/или поперечной акустической волны.

14. Способ по п. 1, в соответствии с которым отобранный образец по меньшей мере один раз насыщают флюидом с известными свойствами, отличающимися от свойств воздуха не менее чем в десять раз, измеряют теплопроводность насыщенного образца и дополнительно сравнивают измереную теплопроводность насыщенного образца и рассчитанную теплопроводность.

15. Способ по п. 1, в соответствии с которым дополнительно измеряют зависимость теплопроводности образца от времени, температуры и/или давления, на основе созданной петрофизической модели пласта-коллектора рассчитывают соответствующую зависимость теплопроводности образца от времени, температуры и/или давления, сравнивают измеренную и рассчитанную зависимости и дополнительно обеспечивают совпадение измеренной и рассчитанной зависимостей теплопроводности образца от времени, температуры и/или давления.