Способ измерения формы поперечных сечений на кругломерах

Способ измерения формы поперечных сечений на кругломерах

Иллюстрации

Показать все

Реферат

Способ относится к области технических измерений и может быть использован при измерении формы поперечных сечений сложного профиля, а также отклонений от круглости номинально круглых сечений.

Известен способ контроля формы поршней и устройство для его осуществления, патент РФ №2403535, в котором устанавливают поршень на стол без точной центровки относительно оси вращения шпинделя, с помощью датчика определяют координаты точек профиля поперечного сечения относительно оси вращения, проводят гармонический анализ совокупности найденных координат, с учетом известного смещения измерительной оси датчика относительно оси вращения рассчитывают эксцентриситет центра средней окружности сечения и его фазу по формулам с учетом результатов гармонического анализа и сделанных допущений, рассчитывают радиусы, соединяющие точки профиля с центром средней окружности в функции угла поворота шпинделя, приводят полученные радиусы к угловой координате профиля сечения. Способ имеет недостатки, так как требует точного знания смещения измерительной оси датчика относительно оси вращения и предполагает, что базовая точка отсчета датчика совпадает с осью вращения. В противном случае, эксцентриситет и его фаза вычисляются с погрешностями, что приводит к ошибкам в определении угловых координат точек профиля сечения. Кроме того, появляются дополнительные погрешности вследствие сделанных допущений при измерении профилей со значительными некруглостями.

Известен способ измерения на кругломерах поперечных сечений без предварительного центрирования (см. Никольский А.А., Королев В.В. Точный метод измерений на кругломерах формы поперечных сечений сложного профиля без предварительного центрирования // Измерительная техника, 2011, №6. - С. 24-29) (прототип). В способе устанавливают изделие на стол с образцовым вращением без точного центрирования, определяют с помощью датчика координаты точек профиля поперечного сечения относительно оси вращения, итерационным методом, по критерию минимизации амплитуды первой гармоники очередного приближения формы профиля сечения в его угловых координатах определяют с учетом известного смещения измерительной оси датчика относительно оси вращения эксцентриситет центра средней окружности сечения и его фазу, рассчитывают радиусы, соединяющие точки профиля сечения с центром его средней окружности в функции угла поворота стола, приводят полученные радиусы к угловым координатам точек профиля сечения.

Способ устраняет недостатки предыдущего посредством применения точного итерационного метода определения эксцентриситета центра средней окружности и его фазы, но также предполагает точное знание смещения измерительной оси датчика относительно оси вращения и совпадение с ней базовой точки отчета датчика, что является недостатком.

Техническая задача, решаемая предлагаемым изобретением, состоит в повышении точности измерения на кругломерах поперечных сечений при высокой производительности, снижении требований по точности изготовления элементов конструкции кругломера, по точности юстировки измерительных осей прибора, а также в снижении требований к условиям его эксплуатации.

Поставленная задача решается тем, что в известном способе измерения формы поперечных сечений изделий на кругломерах, в котором устанавливают изделие на стол с образцовым вращением без точного центрирования, определяют с помощью датчика координаты точек профиля сечения относительно оси вращения, итерационным методом, по критерию минимизации амплитуды первой гармоники очередного приближения профиля сечения в его угловых координатах определяют с учетом известного смещения измерительной оси датчика относительно оси вращения эксцентриситет центра средней окружности сечения и его фазу, рассчитывают радиусы, соединяющие точки профиля сечения с центром его средней окружности в функции угла поворота стола, приводят полученные радиусы к угловым координатам точек профиля сечения, согласно изобретению координаты точек профиля сечения относительно оси вращения определяют для трех различных расположений изделия относительно стола, для каждого расположения изделия итерационным методом, по критерию минимизации амплитуды первой гармоники очередного приближения формы профиля сечения в его угловых координатах находят совокупность различных значений эксцентриситетов, их фаз и амплитуд выбранной гармоники спектра профиля при различных сочетаниях смещений измерительной оси датчика и его базы относительно оси вращения, выбранных из заданных диапазонов возможных значений указанных смещений, итерационным методом из полученной совокупности сочетаний амплитуд выбранной гармоники спектра профиля и возможных значений смещений по критерию равенства их соответствующих значений для одного сечения при трех его различных расположениях определяются указанные смещения, а по найденным смещениям для любого из указанных расположений определяют соответствующие величины эксцентриситета центра средней окружности, его фазы и радиусы, описывающие профиль сечения в его угловых координатах.

На рисунке представлена схема измерения.

Теоретическое обоснование заявляемого способа заключается в следующем.

Если, аналогично прототипу, угловые координаты всех точек профиля сечения рассматриваются относительно центра его средней окружности, то в составе спектра его гармоник отсутствует первая и такой профиль описывается тригонометрическим многочленом вида:

где R₀ - радиус средней окружности профиля (нулевая гармоника);

R_k - амплитуда k-й гармоники профиля сечения (k=2, 3, …, n);

θ₀k - начальный угол k-й гармоники профиля.

При этом константа R₀ в (1) описывает радиус средней окружности профиля, а члены под знаком суммы - отклонения профиля от этой средней окружности в направлении ее радиусов.

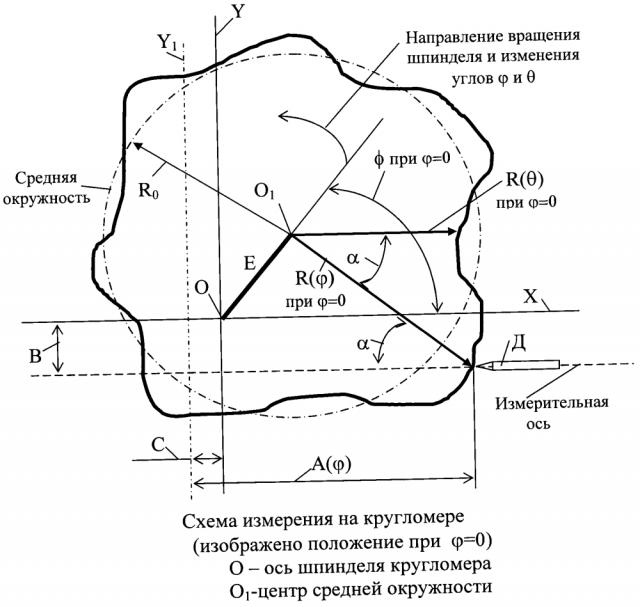
Типовая схема контроля поперечного сечения на кругломере при неточном предварительном центрировании показана ниже.

При точной юстировке прибора измерительная ось датчика Д. должна пересекаться с осью вращения шпинделя в точке О и совпадать с одной из двух декартовых неподвижных координатных осей - с осью X прибора. Однако в общем случае, из-за погрешностей юстировки измерительная ось прибора может не совпадать с осью X, а проходить параллельно ей на некотором расстоянии В. На схеме изображен частный случай неидеального взаимного расположения осей, когда измерительная ось проходит ниже оси X. Для этого случая В<0.

Оси декартовых координат X и Y выбраны так, что через точку О их пересечения проходит ось вращения шпинделя прибора. Предполагается, что вращение шпинделя образцовое и выполняется без прецессий оси. Точка О является также центром полярных координат кругломера, угловая координата ϕ которых является углом поворота шпинделя и отсчитывается от оси X.

Датчик Д, щуп которого перемещается вдоль измерительной оси, при его точном базировании в координатах прибора фиксирует расстояние А, отсчитываемое от оси Y прибора до точки контакта щупа с контролируемым профилем.

Однако в общем случае, датчик базируется с ошибкой С и поэтому фиксирует расстояние А не от оси Y, а от некоторой параллельной ей оси Y₁, отстоящей от оси Y на расстояние С. На схеме изображен частный случай неточного базирования датчика, при котором ось Y₁ расположена левее оси Y и С<0.

Схема измерений изображена в начальный момент, когда угол поворота шпинделя ϕ, отсчитываемый от неподвижной оси X, равен нулю. Поскольку в положении, зафиксированном на схеме, угол ϕ равен нулю, можно лишь указать направление его изменения при вращении шпинделя. В процессе измерения шпиндель кругломера вращается в направлении изменения угла ϕ, указанном на схеме, а прибор фиксирует расстояние А при каждом значении угла ϕ. В процессе совершения полного оборота шпинделя формируется совокупность координат точек профиля сечения А(ϕ) как функция угла поворота шпинделя ϕ в диапазоне его изменений от 0 до 2π.

На схеме показан профиль измеряемого сечения со средней окружностью априори неизвестного радиуса R₀, эксцентрично расположенной по отношению к оси О шпинделя прибора. Центр O₁ этой средней окружности при неточном предварительном центрировании смещен по отношению к оси шпинделя О кругломера на некоторый эксцентриситет с априори неизвестными модулем Е и начальной фазой φ. В начальный момент - при ϕ=0 - угол φ отсчитывается от оси X. В процессе поворота шпинделя вместе с ним вращается и измеряемое сечение. При этом эксцентриситет изменяет свою ориентацию в координатах прибора, занимая по отношению к оси X угловое положение ϕ+φ.

При вращении шпинделя радиус профиля R(θ) будем всегда определять как расстояние от «плавающего» в координатах прибора центра O₁ средней окружности до точки профиля находящейся на линии, проведенной из О₁ параллельно измерительной оси.

На схеме видно, что в начальный момент (при ϕ=0) угловая координата профиля контролируемого сечения R(θ) определится как θ=α(0), где α(0) - угол, который можно рассчитать по (2) при ϕ=0. При вращении шпинделя угловая координата θ профиля изменяется в том же направлении, что и угол поворота шпинделя ϕ, однако значения θ и ϕ всегда будут отличаться друг от друга на угол α, который, в свою очередь, зависит от ϕ в соответствии с (2).

Согласно схеме радиусы R(ϕ), соединяющие контролируемые датчиком точки профиля с центром O1 его средней окружности, связаны с А(ϕ) следующим трансцендентным уравнением:

где α(ϕ)=arctg{[Е sin(ϕ+φ)-В]/[А(ϕ)+С-Е cos(ϕ+φ)]}.

Функции R(θ) и R(ϕ), описанные в формулах (1) и (2), различаются своими аргументами θ и ϕ. Угловая координата точки профиля сечения θ связана, согласно схеме измерений, с углом поворота шпинделя ϕ кругломера следующей зависимостью:

При выполнении измерений на компьютеризированном приборе совокупность точек А(ϕ) формируется не как непрерывная функция угла ϕ поворота шпинделя кругломера, а как множество, включающее N элементов А(ϕ_i) (i=1, 2, …, N), равномерно распределенных по углу ϕ на интервале его изменения от 0 до 2π.

Радиус R(ϕ_i), проведенный к соответствующей i-й точке профиля из центра средней окружности O₁ при известных значениях В, С, Е и φ может быть рассчитан из А(ϕ_i) по формулам (2). Множество, включающее N радиусов R(ϕ_i), также равномерно распределено по углу ϕ на интервале его изменения от 0 до 2π.

Для расчета множества, включающего N радиусов R(θ_i) следует выполнить замену аргументов в R(ϕ_i) в соответствии с выражением (3):

Переход от R(θ_i) к его представлению в форме тригонометрического многочлена (1) требует применения к R(θ_i) операций гармонического анализа.

Радиусы R(θ_i) и R[ϕ_i+α(ϕ_i)] - суть одни и те же радиусыЮ проведенные из центра O1. Однако если множество радиусов R(ϕ_i) равномерно распределено по углу ϕ, то множество радиусов R(θ_i) уже не будет распределено равномерно по углу θ, поскольку α(ϕ)≠const. Поэтому к множеству радиусов R(θ_i) не могут быть применены формулы гармонического анализа (или их дискретные аналоги - формулы Бесселя) без предварительной нормализации - т.е. интерполяции множества с пересчетом к равномерному распределению по углу θ (аналогично прототипу).

Очевидно, что для юстировочных параметров В и С, характеризующих «грубость» юстировки кругломера, всегда можно указать область их возможных значений:

Задачей предлагаемого способа измерения формы поперечных сечений на кругломерах является точное определение формы профиля сечения в его угловых координатах R(θ) (1) на основе обработки совокупности найденных координат точек профиля сечения относительно оси вращения А(ϕ_i) при априори неизвестном эксцентриситете центра средней окружности сечения Е, его фазы φ, а также смещений измерительной оси датчика В и его базы С относительно оси вращения.

Очевидно, что если неизвестные параметры В, С, Е и φ тем или иным способом будут точно определены, то, используя выражения (2) и (3) по найденным значениям А(ϕ_i), аналогично прототипу, можно после соответствующей нормализации (см. выше) и гармонического анализа получить и искомый профиль (1).

Часть поставленной задачи в прототипе уже была решена. Был предложен точный метод определения формы профилей R(θ) поперечных сечений на основе анализа совокупности координат точек профиля сечения А(ϕ), полученных в процессе одного измерения согласно приведенной ниже схеме при априори неизвестных параметрах эксцентриситета Е и φ, но при отсутствии ошибок базирования датчика С=0, а также при известной неточности совмещения осей прибора В. Для точного определения неизвестных Е и φ предложен итерационный метод очередного приближения по критерию минимизации амплитуды первой гармоники R₁ разложения профиля R(θ) по Фурье, проведен расчет радиусов, соединяющих точки профиля сечения с центром его средней окружности в функции угла поворота стола, полученные радиусы приведены к угловым координатам точек профиля.

Выше приведено выражение (2), описывающее геометрические соотношения при измерениях на кругломере и учитывающее не только юстировочный параметр В, как в прототипе, но и ошибку базирования измерительного датчика С.

В основу предлагаемого здесь способа, который должен работать в условиях априорной неопределенности параметров Е, φ, В и С, положена идея совместной обработки результатов нескольких измерений (не более трех) одного профиля при разных его расположениях относительно оси О, достигаемых смещениями профиля в плоскости координат (X, Y) прибора:

Здесь и далее верхним индексом в скобках обозначен порядковый номер измерения I, соответствующих параметров расположения профиля Е^(I) и φ^(I) и спектра амплитуд профиля, найденного из анализа I-го измерения

Согласно прототипу, параметры расположения профиля E^(I)_K,L и φ^(I)_K,L, отвечающие каждому I-му измерению (7), могут быть найдены, если задать в (2) конкретные значения юстировочных параметров В=В_К и C=C_L. Поскольку юстировочные параметры прибора априори неизвестны, то процедуру точного отыскания E^(I)_K,L и φ^(I)_K,L для каждой I-й реализации А^(I)(ϕ) следует выполнить многократно, каждый раз подставляя в (2) параметры В=В_К и C=C_L (K=1, 2, …; L:=1, 2, …). Значения подставляемых параметров В_К и C_L выбираются из диапазонов (5, 6) их возможных значений так, чтобы полностью перекрыть эти диапазоны. В результате для каждого I-го измерения А^(I)(ϕ) (расположения профиля) будет получено множество значений возможных параметров расположения E^(I)_K,L и φ^(I)_K,L, а также множество спектров амплитуд (8) как функций двумерного множества возможных параметров юстировки В_K и C_L:

Если к элементам (9) применить аппроксимацию (например, сплайн-аппроксимацию), то каждый элемент спектра амплитуд предстанет как непрерывная функция параметров юстировки В и С:

Идея предлагаемого способа основана на том, что, как бы мы ни располагали измеряемый профиль в координатах кругломера (то есть какими бы ни были параметры его расположения Е^(I) и φ^(I) для каждого I-го измерения), спектр амплитуд (10) будет одинаковым, так как измеряется одно сечение. При этом значения параметров В и С, подставляемые в (2) из известного диапазона (5, 6), будут соответствовать действительным параметрам юстировки прибора, при которых выполнялись измерения.

Таким образом, для отыскания действительных параметров юстировки прибора достаточно теперь разрешить относительно трех априори неизвестных R_k, В и С систему уравнений:

В геометрической трактовке каждый элемент спектра (11) описывает поверхность в трехмерных декартовых координатах {R^(I)_k, В, С}. Три такие поверхности, построенные в тех же координатах для трех измерений А^(I)(ϕ) (I=1, 2, 3), пересекаются между собой, причем точка их пересечения отвечает искомому сочетанию юстировочных параметров В и С, при которых были проведены все три измерения. Заметим, что в (11) используются амплитуды какой-либо одной k-й из многих возможных гармоник (k=0, 2, 3, …, n). Какую гармонику выбрать для решения уравнений (11), принципиального значения не имеет, ибо решение в отношении искомых В и С при любом k будет одинаковым. Предпочтительно, однако, использовать для решения (11) гармоники, для которых R^(I)_k(B, С)>>0 при всех В и С из диапазонов их возможных значений (5), (6). К числу таких гармоник для профилей всех видов относится нулевая гармоника k=0. Для ожидаемых овальных профилей можно использовать вторую гармонику, для треугольных - третью и т.д.

Последовательность действий при выполнении измерений

Прежде всего, выбирается допустимая погрешность ε>0 определения искомых параметров расположения профиля Е и φ.

Кроме того, в соответствии с ожидаемой формой профиля (круг, овал и т.п., см. выше), выбирается превалирующая k-я гармоника его спектра, амплитуда которой будет использоваться при составлении и решении системы уравнений (11) для окончательного определения искомых параметров Е, φ, В и С.

Дальнейшие действия выполняются в следующем порядке:

1. Изделие ставится на стол без точного центрирования, на полном обороте шпинделя кругломера фиксируются значения координат точек профиля измеряемого сечения А⁽¹⁾(ϕ_i) (i=1, 2, 3, …, N).

2. Выбирается пара конкретных параметров В_K и C_L из диапазонов их возможных значений (5, 6).

3. В соответствии с процедурами итерационного метода, описанного в прототипе, по критерию минимизации амплитуды первой гармоники разложения профиля R(θ) по Фурье, при использовании формулы (2), с погрешностью не более ε определяются E⁽¹⁾_K,L и φ⁽¹⁾_K,L, а также k-я амплитуда R⁽¹⁾_k(B_K, C_L) спектра (9) для выбранной пары значений В_K и C_L.

4. Затем пункты 2-3 выполняются для новой пары параметров В_K и C_L и далее многократно до тех пор, пока не будет получено множество значений R⁽¹⁾_k(В_K,C_L), отвечающее всем выбранным точкам из диапазонов возможных значений В и С (5, 6).

5. Выполняется аппроксимация полученного множества точек R⁽¹⁾_k(B_K, C_L) непрерывной функцией R⁽¹⁾_k(B, С).

2. Контролируемый профиль подвергается смещению в плоскости координат X, Y прибора. Затем, на полном обороте шпинделя фиксируется вторая совокупность координат точек профиля сечения А⁽²⁾(ϕ_i) и к ней применяется последовательность действий, описанных в пунктах 2-5, с получением функции R⁽²⁾_k(B, С). Далее профиль подвергается новому смещению, фиксируется третья совокупность координат точек профиля сечения А⁽³⁾(ϕ_i) и обрабатывается в том же порядке (по пунктам 2-5) с получением функции R⁽³⁾_k(B, С).

3. Система уравнений (11), составленная из трех (I=1, 2, 3) полученных функций R^(I)_k(B, С), разрешается относительно искомых В и С любым из известных способов.

8. Теперь, при известных В и С, согласно п. 3, определяются эксцентриситет Е и фаза φ любого из трех расположений сечения. По формулам (2, 3) с учетом уже известных значений А(ϕ_i) для каждого расположения, согласно прототипу, проводятся расчет соответствующих значений R(ϕ_i), R(θ_i), нормализация, аппроксимация непрерывной функцией R(θ), а после гармонического анализа определяется тригонометрический многочлен (1), описывающий искомый профиль измеряемого сечения.

Высокая точность предлагаемого способа основана на использовании строгого, лишенного каких-либо упрощений описания геометрических соотношений (2, 3) при измерении.

В отличие от известных, предлагаемый способ позволяет выполнять измерение формы сложных профилей с любой наперед заданной точностью без предварительного центрирования изделий, а также при грубой юстировке измерительной оси и неточном базировании измерительного датчика в координатах прибора. Способ предназначен для измерения формы как номинально круглых профилей, так и профилей с заданными отклонениями от круглости, имеющими сложный гармонический состав, например некруглых валов и отверстий, поршней, кулачков, лопастей, обечаек и других изделий.

Способ измерения формы поперечных сечений изделий на кругломерах, в котором устанавливают изделие на стол с образцовым вращением без точного центрирования, определяют с помощью датчика координаты точек профиля сечения относительно оси вращения, итерационным методом, по критерию минимизации амплитуды первой гармоники очередного приближения формы профиля сечения в его угловых координатах определяют с учетом известного смещения измерительной оси датчика относительно оси вращения эксцентриситет центра средней окружности сечения и его фазу, рассчитывают радиусы, соединяющие точки профиля сечения с центром его средней окружности в функции угла поворота стола, приводят полученные радиусы к угловым координатам точек профиля сечения, отличающийся тем, что координаты точек профиля сечения относительно оси вращения определяют для трех различных расположений изделия относительно стола, для каждого расположения изделия итерационным методом, по критерию минимизации амплитуды первой гармоники очередного приближения формы профиля сечения в его угловых координатах находят совокупность различных значений эксцентриситетов, их фаз и амплитуд выбранной гармоники спектра профиля при различных сочетаниях смещений измерительной оси датчика и его базы относительно оси вращения, выбранных из заданных диапазонов возможных значений указанных смещений, итерационным методом из полученной совокупности сочетаний амплитуд выбранной гармоники спектра профиля и возможных значений смещений по критерию равенства их соответствующих значений для одного сечения при трех его различных расположениях определяют указанные смещения, а по найденным смещениям для любого из указанных расположений определяют соответствующие величины эксцентриситета центра средней окружности, его фазы и радиусы, описывающие профиль сечения в его угловых координатах.