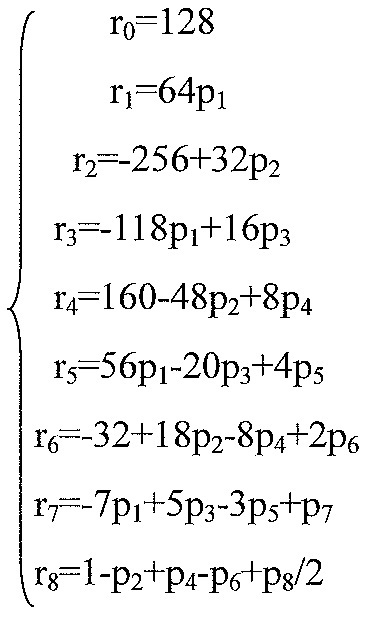Устройство преобразования коэффициентов линейного предсказания и способ преобразования коэффициентов линейного предсказания

Устройство преобразования коэффициентов линейного предсказания и способ преобразования коэффициентов линейного предсказания

Иллюстрации

Показать все

Реферат

ОПИСАНИЕ ИЗОБРЕТЕНИЯ

Область техники

[0001] Настоящее изобретение относится к устройству преобразования коэффициентов линейного предсказания и способу преобразования коэффициентов линейного предсказания.

Уровень техники

[0002] Авторегрессионная полюсная модель представляет собой способ, который часто используется для моделирования кратковременной спектральной огибающей в кодировании аудио и речи, где входной сигнал получается для некоторого совместного блока или кадра с точно определенной длиной, параметр модели кодируется и передается декодеру вместе с другим параметром в качестве информации передачи. Авторегрессионная полюсная модель, в общем, оценивается посредством линейного предсказания и представлена в качестве фильтра синтеза линейного предсказания.

[0003] Одна из последних типичных техник кодирования аудио и речи представляет собой Рекомендацию G.718 ITU-T. Данная рекомендация подробно описывает типичную структуру кадра для кодирования с использованием фильтра синтеза линейного предсказания и способ оценки, способ кодирования, способ интерполяции и способ использования фильтра синтеза линейного предсказания. Дополнительно, кодирование аудио и речи на основе линейного предсказания также подробно описывается в патентной литературе 2.

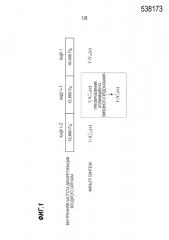
[0004] В кодировании аудио и речи, которое может обрабатывать различные частоты дискретизации ввода/вывода и работать при широком диапазоне скорости передачи битов, которая изменяется от кадра к кадру, в общем, необходимо изменять внутреннюю частоту дискретизации кодера. Поскольку такая же операция также необходима в декодере, декодирование выполняется при одной и той же внутренней частоте дискретизации, что и в кодере. Фиг. 1 показывает пример, где изменяется внутренняя частота дискретизации. В этом примере, внутренняя частота дискретизации равна 16.000 Гц в кадре i, и она равна 12.800 Гц в предыдущем кадре i-1. Фильтр синтеза линейного предсказания, который представляет характеристики входного сигнала в предыдущем кадре i-1, должен быть снова оценен после повторной дискретизации входного сигнала при измененной внутренней частоте дискретизации 16.000 Гц или преобразован в фильтр синтеза линейного предсказания, соответствующий измененной внутренней частоте дискретизации 16.000 Гц. Причина того, что фильтр синтеза линейного предсказания должен быть вычислен при измененной внутренней частоте дискретизации, заключается в получении корректного внутреннего состояния фильтра синтеза линейного предсказания для текущего входного сигнала и выполнении интерполяции, для того чтобы получить модель, которая является по времени более выравненной.

[0005] Один способ для получения другого фильтра синтеза линейного предсказания на основе характеристик некоторого фильтра синтеза линейного предсказания представляет собой вычисление фильтра синтеза линейного предсказания после преобразования из желательной частотной характеристики после преобразования в частотной области, как показано на Фиг. 2. В этом примере, коэффициенты LSF вводятся в качестве параметра, представляющего фильтр синтеза линейного предсказания. Это могут быть коэффициенты LSP, коэффициенты ISF, коэффициенты ISP или коэффициенты отражения, которые, в общем, известны в качестве параметров, эквивалентных коэффициентам линейного предсказания. Сначала, вычисляются коэффициенты линейного предсказания, для того чтобы получить спектр мощности Y(ω) фильтра синтеза линейного предсказания при первой внутренней частоте дискретизации (этап 001). Этот этап может быть пропущен, когда коэффициенты линейного предсказания известны. Далее вычисляется спектр мощности Y(ω) фильтра синтеза линейного предсказания, который определяется полученными коэффициентами линейного предсказания (этап 002). Затем полученный спектр мощности модифицируется в желательный спектр мощности Yʹ(ω) (этап 003). Коэффициенты автокорреляции вычисляются из модифицированного спектра мощности (этап 004). Коэффициенты линейного предсказания вычисляются из коэффициентов автокорреляции (этап 005). Отношение между коэффициентами автокорреляции и коэффициентами линейного предсказания является известным в качестве уравнения Юла-Уокера, и алгоритм Левинсона-Дарбина является хорошо известным как решение этого уравнения.

[0006] Этот алгоритм является эффективным в преобразовании частоты дискретизации вышеописанного фильтра синтеза линейного предсказания. Причина состоит в том, что хотя сигнал, который во времени находится впереди сигнала в кадре для кодирования, который называется сигналом предсказания, в общем, используется в анализе линейного предсказания, упомянутый сигнал предсказания не может быть снова использован при выполнении анализа линейного предсказания в декодере.

[0007] Как описано выше по тексту, в кодировании аудио и речи с двумя различными внутренними частотами дискретизации предпочтительно использовать спектр мощности, для того чтобы преобразовывать внутреннюю частоту дискретизации известного фильтра синтеза линейного предсказания. Однако, поскольку вычисление спектра мощности является сложным вычислением, имеется проблема, заключающаяся в том, что объем вычислений является большим.

Список библиографических ссылок

Непатентная литература

[0008] Непатентная литература 1: ITU-T Recommendation G.718

Непатентная литература 2: Speech coding and synthesis, W.B. Kleijn, K.K. Pariwal, et al. ELSEVIER.

Сущность изобретения

Техническая проблема

[0009] Как описано выше по тексту, существует проблема, заключающаяся в том, что в схеме кодирования, которая имеет фильтр синтеза линейного предсказания с двумя различными внутренними частотами дискретизации, требуется большой объем вычислений для преобразования фильтра синтеза линейного предсказания при некоторой внутренней частоте дискретизации в фильтр синтеза линейного предсказания при желательной внутренней частоте дискретизации.

Решение проблемы

[0010] Для решения вышеуказанной проблемы, устройство преобразования коэффициентов линейного предсказания согласно одному аспекту настоящего изобретения является устройством, которое преобразует первые коэффициенты линейного предсказания, вычисляемые при первой частоте дискретизации, во вторые коэффициенты линейного предсказания при второй частоте дискретизации, отличной от первой частоты дискретизации, которое включает в себя средство для вычисления, на действительной оси единичной окружности, спектра мощности, соответствующего вторым коэффициентам линейного предсказания при второй частоте дискретизации, на основе первых коэффициентов линейного предсказания или эквивалентного параметра, средство для вычисления, на действительной оси единичной окружности, коэффициентов автокорреляции из спектра мощности, и средство для преобразования коэффициентов автокорреляции во вторые коэффициенты линейного предсказания при второй частоте дискретизации. В этой конфигурации возможно эффективно сокращать объем вычислений.

[0011] Дополнительно, в устройстве преобразования коэффициентов линейного предсказания согласно одному аспекту настоящего изобретения, спектр мощности, соответствующий вторым коэффициентам линейного предсказания, может быть получен посредством вычисления спектра мощности с использованием первых коэффициентов линейного предсказания в точках на действительной оси, соответствующих числу N1 различных частот, где N1=1+(F1/F2)(N2-1), когда первая частота дискретизации равна F1 и вторая частота дискретизации равна F2 (где F1<F2), и экстраполяции спектра мощности, вычисленного с использованием первых коэффициентов линейного предсказания для числа (N2-N1) компонентов спектра мощности. В этой конфигурации возможно эффективно сокращать объем вычислений, когда вторая частота дискретизации является более высокой, чем первая частота дискретизации.

[0012] Дополнительно, в устройстве преобразования коэффициентов линейного предсказания согласно одному аспекту настоящего изобретения, спектр мощности, соответствующий вторым коэффициентам линейного предсказания, может быть получен посредством вычисления спектра мощности с использованием первых коэффициентов линейного предсказания в точках на действительной оси, соответствующих числу N1 различных частот, где N1=1+(F1/F2)(N2-1), когда первая частота дискретизации равна F1 и вторая частота дискретизации равна F2 (где F1<F2). В этой конфигурации возможно эффективно сокращать объем вычислений, когда вторая частота дискретизации является более низкой, чем первая частота дискретизации.

[0013] Один аспект настоящего изобретения может быть описан как изобретение по объекту устройство, как упомянуто выше по тексту, и в дополнение также может быть описан как изобретение по объекту способ следующим образом. Они попадают под различные категории, но по существу являются одним и тем же изобретением и достигают аналогичной работы и эффектов.

[0014] В частности, способ преобразования коэффициентов линейного предсказания согласно одному аспекту настоящего изобретения является способом преобразования коэффициентов линейного предсказания, выполняемым устройством, которое преобразует первые коэффициенты линейного предсказания, вычисляемые при первой частоте дискретизации, во вторые коэффициенты линейного предсказания при второй частоте дискретизации, отличной от первой частоты дискретизации, причем способ включает в себя этап, на котором вычисляют, на действительной оси единичной окружности, спектр мощности, соответствующий вторым коэффициентам линейного предсказания при второй частоте дискретизации, на основе первых коэффициентов линейного предсказания или эквивалентного параметра, этап, на котором вычисляют, на действительной оси единичной окружности, коэффициенты автокорреляции из спектра мощности, и этап, на котором преобразовывают коэффициенты автокорреляции во вторые коэффициенты линейного предсказания при второй частоте дискретизации.

[0015] Дополнительно, способ преобразования коэффициентов линейного предсказания согласно одному аспекту настоящего изобретения может получать спектр мощности, соответствующий вторым коэффициентам линейного предсказания, посредством вычисления спектра мощности с использованием первых коэффициентов линейного предсказания в точках на действительной оси, соответствующих числу N1 различных частот, где N1=1+(F1/F2)(N2-1), когда первая частота дискретизации равна F1 и вторая частота дискретизации равна F2 (где F1<F2), и экстраполяции спектра мощности, вычисленного с использованием первых коэффициентов линейного предсказания для числа (N2-N1) компонентов спектра мощности.

[0016] Дополнительно, способ преобразования коэффициентов линейного предсказания согласно одному аспекту настоящего изобретения может получать спектр мощности, соответствующий вторым коэффициентам линейного предсказания, посредством вычисления спектра мощности с использованием первых коэффициентов линейного предсказания в точках на действительной оси, соответствующих числу N1 различных частот, где N1=1+(F1/F2)(N2-1), когда первая частота дискретизации равна F1 и вторая частота дискретизации равна F2 (где F1<F2).

Полезные эффекты изобретения

[0017] Обеспечивается возможность оценивать фильтр синтеза линейного предсказания после преобразования внутренней частоты дискретизации с уменьшенным объемом вычислений, чем в существующих средствах.

Краткое описание чертежей

[0018] Фиг. 1 представляет собой вид, показывающий отношение между переключением внутренней частоты дискретизации и фильтра синтеза линейного предсказания.

Фиг. 2 представляет собой вид, показывающий преобразование коэффициентов линейного предсказания.

Фиг. 3 представляет собой блок-схему последовательности операций преобразования 1.

Фиг. 4 представляет собой блок-схему последовательности операций преобразования 2.

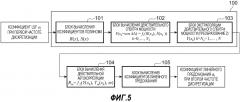
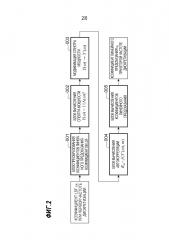
Фиг. 5 представляет собой блок-схему варианта осуществления настоящего изобретения.

Фиг. 6 представляет собой вид, показывающий отношение между единичной окружностью и косинусной функцией.

Описание вариантов осуществления

[0019] Варианты осуществления устройства, способа и программы описаны в дальнейшем в этом документе со ссылкой на чертежи. Следует отметить, что в описании чертежей одинаковые элементы обозначаются одинаковыми ссылочными символами и их избыточное описание пропущено.

[0020] Сначала, в дальнейшем в этом документе описываются определения, необходимые для описания вариантов осуществления.

[0021] Ответ авторегрессионного фильтра линейного предсказания N-го порядка (который упоминается в дальнейшем в этом документе как фильтр синтеза линейного предсказания)

(1)

может быть адаптирован для спектра мощности Y(ω) посредством вычисления автокорреляции

(2) ,

для известного спектра мощности Y(ω) при угловой частоте ω∊[-π, π] и с использованием коэффициентов автокорреляции N-го порядка, решающих коэффициенты линейного предсказания a₁,a₂,…,a_n, например посредством способа Левинсона-Дарбина, как типичного способа.

[0022] Такое генерирование авторегрессионной модели с использованием известного спектра мощности также может быть использовано для модификации фильтра синтеза линейного предсказания 1/A(z) в частотной области. Это достигается посредством вычисления спектра мощности известного фильтра

(3)

и модификации полученного спектра мощности Y(ω) надлежащим способом, который является подходящим с целью получения модифицированного спектра мощности Yʹ(ω), затем осуществляется вычисление коэффициентов автокорреляции Yʹ(ω) посредством вышеуказанного уравнения (2), и осуществляется получение коэффициентов линейного предсказания модифицированного фильтра 1/Aʹ(z) посредством алгоритма Левинсона-Дарбина или аналогичного способа.

[0023] В то время как уравнение (2) не может быть аналитически вычислено, за исключением простых случаев, например аппроксимация прямоугольника может быть использована следующим образом.

(4)

где Ω указывает число M частот, размещенных с регулярными интервалами на угловой частоте [-π,π]. Когда используется симметричность Y(-ω)=-Y(ω), вышеупомянутое дополнение должно только оценивать угловую частоту ω∊ [0, π], которая соответствует верхней половине единичной окружности. Таким образом, исходя из объема вычислений, предпочитается, что аппроксимация прямоугольника, представленная вышеуказанным уравнением (4), изменяется следующим образом

(5)

где Ω указывает число (N-2) частот, размещенных с регулярными интервалами на (0, π), за исключением 0 и π.

[0024] В дальнейшем в этом документе частоты спектральной линии (которые в дальнейшем в этом документе упоминаются как LSF), как эквивалентные средства выражения коэффициентов линейного предсказания, описываются в дальнейшем в этом документе.

[0025] Представление посредством LSF используется в различных техниках кодирования аудио и речи для величины особенности фильтра синтеза линейного предсказания, и для работы и кодирования фильтра синтеза линейного предсказания. LSF уникально характеризует полином A(z) N-го порядка числом n параметров, которые отличаются от коэффициентов линейного предсказания. LSF имеет такие характеристики: она легко гарантирует стабильность фильтра синтеза линейного предсказания, она интуитивно интерпретируется в частотной области, она с меньшей долей вероятности будет затронута ошибками квантования, чем другие параметры, такие как коэффициенты линейного предсказания и коэффициенты отражения, она является подходящей для интерполяции и подобного.

[0026] С целью одного варианта осуществления настоящего изобретения, LSF задается следующим образом.

[0027] Декомпозиция LSF полинома A(z) N-го порядка может быть представлена следующим образом посредством использования смещения целого числа, где κ≥0

(6) A(z)={P(z)+Q(z)}/2

где P(z)=A(z)+z^-n-κA(z^-1) и

Q(z)=A(z)-z^-n-κA(z^-1)

Уравнение (6) указывает, что P(z) является симметричным и Q(z) является антисимметричным следующим образом

P(z)=z^-n-κP(z^-1)

Q(z)= -z^-n-κQ(z^-1)

Такая симметричность является важной характеристикой в декомпозиции LSF.

[0028] Ясно, что P(z) и Q(z) каждый имеют корень на z=±1. Эти явные корни показаны в таблице 1 как n и κ. Таким образом, полиномы, представляющие явные корни P(z) и Q(z), заданы как P_T(z) и Q_T(z), соответственно. Когда P(z) не имеет явного корня, P_T(z) равен 1. То же самое применяется к Q(z).

[0029] LSF A(z) является нетривиальным корнем положительного фазового угла P(z) и Q(z). Когда полином A(z) является минимальной фазой, то есть, когда все корни A(z) находятся внутри единичной окружности, нетривиальные корни P(z) и Q(z) распределяются в качестве альтернативы на единичной окружности. Число комплексных корней P(z) и Q(z) соответственно равно m_P и m_Q. Таблица 1 показывает отношение m_P и m_Q с порядком n и смещением κ.

[0030] Когда комплексные корни P(z), который является положительным фазовым углом, представляются в качестве

и корни Q(z) представляются в качестве

,

положения корней полинома A(z), который является минимальной фазой, могут быть представлены следующим образом.

(7)

[0031] В кодировании аудио и речи используется смещение κ=0 или κ=1. Когда κ=0, это, в общем, называется спектральной частотой иммитанса (ISF), и когда κ=1, это, в общем, называется LSF в более узком смысле, чем тот, что в описании одного варианта осуществления настоящего изобретения. Однако следует отметить, что представление с использованием смещения может обрабатывать и ISF и LSF унифицированным способом. Во многих случаях результат, полученный посредством LSF, может быть и так применен к заданному κ≥0 или может быть обобщен.

[0032] Когда κ=0, представление LSF имеет только число (m_P+m_Q=n-1) параметров частоты, как показано в таблице 1. Таким образом, требуется еще один параметр, чтобы уникально представлять A(z), и типично используется n-й коэффициент отражения (который упоминается в дальнейшем в этом документе как γ_n) A(z). Этот параметр вводится в декомпозицию LSF как следующий множитель.

(8) υ=-(γ_n+1)/(γ_n-1)

где γ_n является n-м коэффициентом отражения A(z), который начинается с Q(z), и он типично равен γ_n=a_n.

[0033] Когда κ=1, число (m_P+m_Q=n) параметров получаются посредством декомпозиции LSF, и возможно уникально представлять A(z). В этом случае, υ=1.

Таблица 1

Случай
(1)	четное число	0	n/2	n/2-1	1	z2-1	-(γn+1)/(γn-1)
(2)	нечетное число	0	(n-1)/2	(n-1)/2	z+1	z-1	-(γn+1)/(γn-1)
(3)	четное число	1	n/2	n/2	z+1	z-1	1
(4)	нечетное число	1	(n+1)/2	(n-1)/2	1	z2-1	1

[0034] Учитывая тот факт, что неявные корни, за исключением явных корней, являются парой комплексных чисел на единичной окружности и получают симметричные полиномы, получается следующее уравнение.

(9)

)

Аналогичным образом,

(10)

В этих полиномах,

и

полностью представляют P(z) и Q(z) посредством использования заданного смещения κ и ν, которое определяется порядком n A(z). Эти коэффициенты могут быть непосредственно получены из выражений (6) и (8).

[0035] Когда z=e^jω и с использованием следующего отношения

выражения (9) и (10) могут быть представлены следующим образом

(11)

(12)

где

(13)

и

(14)

[0036] В частности, LSF полинома A(z) является корнями R(ω) и S(ω) на угловой частоте ω∊ (0, π).

[0037] Полиномы Чебышева первого рода, которые используются в одном варианте осуществления настоящего изобретения, описаны в дальнейшем в этом документе.

[0038] Полиномы Чебышева первого рода заданы следующим образом с использованием рекуррентного соотношения

(15) T_k+1(x)=2xT_k(x)-T_k-1(x) k=1,2,…

Следует отметить, что исходные значения представляют собой T₀(x)=1 и T₁(x)=x, соответственно. Для x, где [-1, 1], полиномы Чебышева могут быть представлены следующим образом

(16) T_k(x)=cos{k cos^-1x} k=0,1,…

[0039] Один вариант осуществления настоящего изобретения объясняет, что уравнение (15) обеспечивает простой способ для вычисления coskω (где k=2,3,…), который начинается с cosω и cos0=1. В частности, с использованием уравнения (16), уравнение (15) перезаписывается в следующей форме

(17) coskω=2cosωcos(k-1)ω-cos(k-2)ω k=2,3,…

Когда используется преобразование ω=arccosx, первые полиномы, полученные из уравнения (15), представлены следующим образом

Когда уравнения (13) и (14) для x∊ [-1,1] заменяются этими полиномами Чебышева, получаются следующие уравнения

(18)

(19)

Когда LSFω_i известно для i=0,1,...,m_P+m_Q-1, следующие уравнения получаются с использованием косинуса LSF x_i=cosω_i (LSP)

(20)

(21)

Коэффициенты r₀ и s₀ могут быть получены посредством сравнения уравнений (18) и (19) с (20) и (21) на основе m_P и m_Q.

[0040] Уравнения (20) и (21) записаны как

(22)

(23)

Эти полиномы могут быть эффективно вычислены для заданного x посредством способа, известного как схема Горнера. Схема Горнера получает R(x)=b₀(x) посредством использования следующего рекурсивного отношения

b_k(x)=xb_k+1(x)+r_k

где исходное значение равно

То же самое применяется к S(x).

[0041] Способ вычисления коэффициентов полиномов уравнений (22) и (23) описывается в дальнейшем в этом документе с использованием примера. В этом примере предполагается, что порядок A(z) равен 16 (n=16). Соответственно, в этом случае m_P=m_Q=8. Разложение в ряд уравнения (18) может быть представлено в форме уравнения (22) посредством подстановки и упрощения полиномами Чебышева. В качестве результата, коэффициенты полинома уравнения (22) представлены следующим образом с использованием коэффициента p_i полинома P(z).

Коэффициенты P(z) могут быть получены из уравнения (6). Этот пример также может быть применен к полиному уравнения (23) посредством использования такого же уравнения и с использованием коэффициентов Q(z). Дополнительно, одно и то же уравнение для вычисления коэффициентов R(x) и S(x) может легко выводить другой порядок n, а также смещение κ.

[0042] Дополнительно, когда корни уравнений (20) и (21) известны, коэффициенты могут быть получены из уравнений (20) и (21).

[0043] Схема обработки согласно одному варианту осуществления настоящего изобретения описана в дальнейшем в этом документе.

[0044] Один вариант осуществления настоящего изобретения обеспечивает эффективный способ вычисления и устройство для, при преобразовании фильтра синтеза линейного предсказания, вычисленного заранее кодером или декодером при первой частоте дискретизации, в фильтр синтеза линейного предсказания при второй частоте дискретизации, вычисления спектра мощности фильтра синтеза линейного предсказания и модификации его во вторую частоту дискретизации, и затем получения коэффициентов автокорреляции из модифицированного спектра мощности.

[0045] Способ вычисления для спектра мощности фильтра синтеза линейного предсказания согласно одному варианту осуществления настоящего изобретения описан в дальнейшем в этом документе. Вычисление спектра мощности использует декомпозицию LSF уравнения (6) и свойства полиномов P(z) и Q(z). Посредством использования декомпозиции LSF и вышеописанных полиномов Чебышева, спектр мощности может быть преобразован в действительную ось единичной окружности.

[0046] С помощью преобразования в действительную ось возможно достигать эффективного способа для вычисления спектра мощности на произвольной частоте в ω∊ [0, π]. Причина состоит в том, что возможно оценивать трансцендентные функции, поскольку спектр мощности представлен полиномами. Конкретно, возможно упростить вычисление спектра мощности на ω=0, ω=π/2 и ω=π. Такое же упрощение также применимо к LSF, где одно из P(z) или Q(z) равно нулю. Такие свойства являются преимущественными по сравнению с FFT, которое обычно используется для вычисления спектра мощности.

[0047] Известно, что спектр мощности A(z) может быть представлен следующим образом с использованием декомпозиции LSF.

(26) |A(ω)|²={|P(ω)|²+|Q(ω)|²}/4

[0048] Один вариант осуществления настоящего изобретения использует полиномы Чебышева как способ для более эффективного вычисления спектра мощности |A(ω)|² A(z) по сравнению со случаем непосредственного применения уравнения (26). В частности, спектр мощности |A(ω)|² вычисляется на действительной оси единичной окружности, как представлено следующим уравнением, посредством преобразования переменной в x=cosω и с использованием декомпозиции LSF посредством полиномов Чебышева.

(1)-(4) соответствуют (1)-(4) в таблице 1, соответственно.

[0049] Уравнение (27) доказано следующим образом.

[0050] Следующие уравнения получаются из уравнений (11) и (12).

Множители, которые представляют явные корни P(ω) и Q(ω), соответственно представлены следующим образом.

Применение подстановки cosω=x и cos2ω=2ײ-1 к |P_T(ω₎| и |Q_T(ω₎|, соответственно дает уравнение (27).

[0051] Полиномы R(x) и S(x) могут быть вычислены вышеописанной схемой Горнера. Дополнительно, когда известно x для вычисления R(x) и S(x), вычисление тригонометрической функции может быть пропущено посредством сохранения x в памяти.

[0052] Вычисление спектра мощности A(z) дополнительно может быть упрощено. Сначала, в случае вычисления с LSF, один из R(x) и S(x) в соответствующем уравнении (27) равен нулю. Когда смещение равно κ=1 и порядок n равен четному числу, уравнение (27) упрощается следующим образом.

Дополнительно, в случае ω={0,π/2,π}, оно упрощается, когда x={1,0,-1}. Уравнения представлены следующим образом, когда смещение равно κ=1 и порядок n равен четному числу, которые являются такими же, как в вышеуказанном примере.

|A(ω=0)|²=4R²(1)

|A(ω=π/2)|²=2(R²(0)+S²(0))

|A(ω=π)|²=4S²(-1)

Аналогичные результаты могут быть также легко получены, когда смещение равно κ=0 и порядок n равен нечетному числу.

[0053] Вычисление коэффициентов автокорреляции согласно одному варианту осуществления настоящего изобретения описывается ниже по тексту.

[0054] В уравнении (5), когда задается частота Ω₊=Δ,2Δ,...,(N-1)Δ, где N равно нечетному числу и интервал частот равен Δ=π/(N-1), вычисление автокорреляции содержит вышеописанный упрощенный спектр мощности на ω=0,π/2,π. Поскольку нормализация коэффициентов автокорреляции посредством 1/N не влияет на коэффициенты линейного предсказания, которые должны быть получены в качестве результата, может быть использовано какое-либо положительное значение.

[0055] Все еще, однако, вычисление уравнения (5) требует coskω, где k=1,2,...,n для каждого числа (N-2) частот. Таким образом, используется симметричность coskω.

(28) cos(π-kω)=(-1)^kcos kω, ω∊ (0, π/2)

Следующие характеристики также используются.

(29)

где указывает самое большое целое число, которое не превышает x. Следует отметить, что уравнение (29) упрощается в 2,0,-2,0,2,0,... для k=0,1,2,....

[0056] Дополнительно, посредством преобразования в x=cosω, коэффициенты автокорреляции перемещаются на действительную ось единичной окружности. С этой целью, представлена переменная X(x)=Y(arccos x). Это обеспечивает возможность вычисления coskω посредством использования уравнения (15).

[0057] Данная выше по тексту аппроксимация автокорреляции уравнения (5) может быть заменена следующим уравнением.

(30) где T_k(x)=2xT_k-1(x)-T_k-2(x)

k=2,3,...,n, и T₀(x)=1, T₁(x)=cosx, как описано выше по тексту. Когда учитывается симметричность уравнения (28), последний член уравнения (30) должен быть вычислен только когда x∊Λ={cosΔ,cos2Δ,...,(N-3)Δ/2}, и число (N-3)/2 значений косинуса может быть сохранено в памяти. Фиг. 6 показывает отношение между частотой Λ и косинусной функцией, когда N=31.

[0058] Пример настоящего изобретения описывается в дальнейшем в этом документе. В этом примере используется случай преобразования фильтра синтеза линейного предсказания, вычисленного при первой частоте дискретизации 16.000 Гц, в фильтр синтеза линейного предсказания при второй частоте дискретизации 12.800 Гц (которое в дальнейшем в этом документе упоминается как преобразование 1) и случай преобразования фильтра синтеза линейного предсказания, вычисленного при первой частоте дискретизации 12.800 Гц, в фильтр синтеза линейного предсказания при второй частоте дискретизации 16.000 Гц (в дальнейшем в этом документе как преобразование 2). Те две частоты дискретизации имеют соотношение 4:5 и, в общем, используются в кодировании аудио и речи. Каждое из преобразования 1 и преобразования 2 из этого примера выполняется в отношении фильтра синтеза линейного предсказания в предыдущем кадре, когда внутренняя частота дискретизации изменилась, и оно может быть выполнено в каком-либо кодере и декодере. Такое преобразование требуется для установки корректного внутреннего состояния фильтру синтеза линейного предсказания в текущем кадре и для выполнения интерполяции фильтра синтеза линейного предсказания в соответствии со временем.

[0059] Обработка в этом примере описывается в дальнейшем в этом документе со ссылкой на блок-схемы последовательности операций с Фиг. 3 и 4.

[0060] Для вычисления спектра мощности и коэффициентов автокорреляции посредством использования общей точки частоты в обоих случаях преобразований 1 и 2, число частот, когда частота дискретизации равна 12.800 Гц, определяется как N_L=1+(12.800 Гц/16.000 Гц)(N-1). Следует отметить, что N равно числу частот при частоте дискретизации 16.000 Гц. Как описано ранее, предпочтительно, чтобы и N и N_L являлись нечетными числами, для того чтобы содержать частоты, при которых вычисление спектра мощности и коэффициентов автокорреляции упрощается. Например, когда N равно 31, 41, 51, 61, соответствующее N_L равно 25, 33, 41, 49. Случай, когда N=31 и N_L=25, описан в качестве примера ниже по тексту (этап S000).

[0061] Когда число частот, которые должны быть использованы для вычисления спектра мощности и коэффициентов автокорреляции в области, где частота дискретизации равна 16.000 Гц, равно N=31, интервал частот равен Δ=π/30, и число элементов, необходимых для вычисления автокорреляции, содержащихся в Λ, равно (N-3)/2=14.

[0062] Преобразование 1, которое выполняется в кодере и декодере при вышеуказанных условиях, осуществляется в следующей процедуре.

[0063] Определение коэффициентов полиномов R(x) и S(x) посредством использования уравнений (20) и (21) из корней, полученных посредством смещения κ=0 или κ=1 и LSF, которая соответствуют фильтру синтеза линейного предсказания, полученному при частоте дискретизации 16.000 Гц, которая является первой частотой дискретизации (этап S001).

[0064] Вычисление спектра мощности фильтра синтеза линейного предсказания при второй частоте дискретизации до 6.400 Гц, которая является частотой Найквиста второй частоты дискретизации. Поскольку эта предельная частота соответствует ω=(4/5)π при первой частоте дискретизации, спектр мощности вычисляется с использованием уравнения (27) на числе N_L=25 частот на нижней стороне. Для вычисления R(x) и S(x), схема Горнера может быть использована для сокращения вычисления. Нет необходимости вычислять спектр мощности для остальных 6(=N-N_L) частот на верхней стороне (этап S002).

[0065] Вычисление коэффициентов автокорреляции, соответствующих спектру мощности, полученному на этапе S002 посредством использования уравнения (30). На этом этапе, N в уравнении (30) установлено на N_L=25, которое является числом частот при второй частоте дискретизации (этап S003).

[0066] Вывод коэффициентов линейного предсказания посредством способа Левинсона-Дарбина или аналогичного способа с использованием коэффициента автокорреляции, полученного на этапе S003, и получение фильтра синтеза линейного предсказания при второй частоте дискретизации (этап S004).

[0067] Преобразование коэффициента линейного предсказания, полученного на этапе S004, в LSF (этап S005).

[0068] Преобразование 2, которое выполняется в кодере или декодере, может быть достигнуто в следующей процедуре, таким же способом как преобразование 1.

[0069] Определение коэффициентов полиномов R(x) и S(x) посредством использования уравнений (20) и (21) из корней, полученных посредством смещения κ=0 или κ=1, и LSF, которая соответствует фильтру синтеза линейного предсказания, полученному при частоте дискретизации 12.800 Гц, которая является первой частотой дискретизации (этап