Извлечение реверберирующего звука с использованием микрофонных массивов

Извлечение реверберирующего звука с использованием микрофонных массивов

Иллюстрации

Показать все

Реферат

Нижеследующее изобретение относится к области акустического анализа, записи пространственного звука, обработке сигналов микрофонных массивов, и пространственной фильтрации. Некоторые варианты осуществления настоящего изобретения относятся к способу, который может использоваться для определения коэффициентов фильтрации фильтра рассеянного звука, т.е. фильтра для извлечения рассеянного звука (реверберирующего звука) из записей с использованием микрофонного массива. Некоторые варианты осуществления относятся к соответствующей компьютерной программе. Некоторые варианты осуществления относятся к устройству, которое может быть использовано для определения коэффициентов фильтрации фильтра рассеянного звука.

Захват звука с использованием микрофонного массива в реверберирующих средах обычно направлен на захват прямого звука от источников звука, при ослаблении шума и реверберации. Для многих применений было бы выгодным, если бы можно было также извлекать реверберирующий звук, при подавлении прямого звука и шума. Например, в пространственном воспроизведении звука [Pulkki2007, Thiergart2013, Kowalczyk2013], реверберация, присутствующая на стороне записи, должна быть воспроизведена на стороне воспроизведения для воссоздания необходимого стереофонического эффекта. Кроме того, при обеспечении оценки реверберирующего звука, мы можем вычислить параметры, такие как отношение сигнал-реверберация или мощность реверберирующего звука, которые представляют важную информацию для различных других применений.

В то время как оценка компонентов прямого звука (например, с использованием разделения источников, дереверберации, или подавления шума) хорошо освещена в литературе, существует лишь небольшое количество методик для извлечения реверберирующего звука. Обычно реверберация моделируется в виде (изменяющегося во времени) рассеянного звукового поля. Для извлечения рассеянного звука, в последнее время использовались одноканальные фильтры (например, в [Pulkki2007, Thiergart2013]), которые имеют плохую производительность, когда активно множество источников, или для сигналов, подобных сигналам переходных процессов. Лучшая производительность может быть достигнута с использованием многоканальных фильтров (например, [Kowalczyk2013, Thiergart2013b]). К сожалению, существующие в настоящее время многоканальные фильтры являются неоптимальными и не обеспечивают подходящую диаграмму направленности для захвата рассеянного звука.

Поэтому желательно обеспечить фильтр рассеянного звука, имеющий улучшенную производительность в отношении извлечения рассеянного звука и/или подавления прямого звука. Также, может быть желательным, чтобы фильтр рассеянного звука имел диаграмму направленности, которая является в высшей степени всенаправленной, за исключением направлений поступления компонентов прямого звука. В высшей степени всенаправленная характеристика направленности является желательной, поскольку рассеянный звук поступает на микрофонный массив со всех направлений.

Предложен способ, который содержит определение линейного ограничения для коэффициентов фильтрации фильтра рассеянного звука. Линейное ограничение основано на пространственной когерентности между первым участком рассеянного звука в первом микрофонном сигнале и вторым участком рассеянного звука во втором микрофонном сигнале. Первый микрофонный сигнал захвачен первым микрофоном, а второй микрофонный сигнал захвачен вторым микрофоном, расположенным на расстоянии от первого микрофона, известным способом. Способ также содержит вычисление по меньшей мере одного из направления поступления по меньшей мере одного прямого звука, статистики сигналов в отношении первого и второго микрофонных сигналов и статистики шумов в отношении первого и второго микрофонных сигналов. Способ дополнительно содержит определение коэффициентов фильтрации фильтра рассеянного звука путем решения оптимизационной задачи в отношении по меньшей мере одного из направления поступления по меньшей мере одного прямого звука, статистики сигналов и статистики шумов, с учетом линейного ограничения для коэффициентов фильтрации.

Варианты осуществления обеспечивают компьютерную программу для реализации вышеописанного способа, когда обеспечивается ее исполнение на компьютере или процессоре обработки сигналов.

Дополнительные варианты осуществления обеспечивают устройство, содержащее вычислитель линейного ограничения, выполненный с возможностью определения линейного ограничения для коэффициентов фильтрации фильтра рассеянного звука. Линейное ограничение основано на пространственной когерентности между первым участком рассеянного звука в первом микрофонном сигнале и вторым участком рассеянного звука во втором микрофонном сигнале. Первый микрофонный сигнал захвачен или был захвачен первым микрофоном, а второй микрофонный сигнал захвачен или был захвачен вторым микрофоном, расположенным на расстоянии от первого микрофона, известным способом. Устройство также содержит вычислитель статистики, выполненный с возможностью вычисления по меньшей мере одного из направления поступления по меньшей мере одного прямого звука, статистики сигналов в отношении первого и второго микрофонных сигналов и статистики шумов в отношении первого и второго микрофонных сигналов и второго микрофонного сигнала. Устройство дополнительно содержит вычислитель коэффициентов фильтрации, выполненный с возможностью определения коэффициентов фильтрации фильтра рассеянного звука, путем решения оптимизационной задачи в отношении по меньшей мере одного из направления поступления по меньшей мере одного прямого звука, статистики сигналов и статистики шумов, с учетом линейного ограничения для коэффициентов фильтрации.

Варианты осуществления основаны на понимании того, что фильтр рассеянного звука может быть определен с учетом по меньшей мере одного линейного ограничения, которое относится к участкам рассеянного звука микрофонных сигналов.

Далее варианты осуществления настоящего изобретения описаны более подробно со ссылкой на чертежи, на которых:

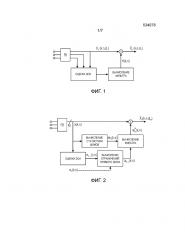
Фиг. 1 показывает схематичную блок-схему методики для извлечения рассеянного звука с использованием одноканального фильтра;

Фиг. 2 показывает схематичную блок-схему методики для извлечения рассеянного звука с использованием многоканального фильтра;

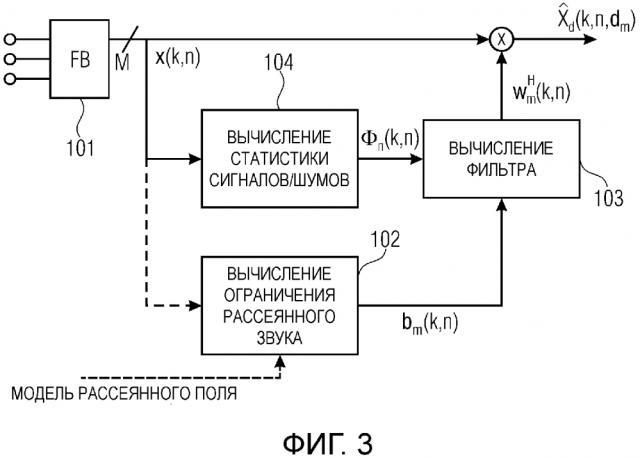
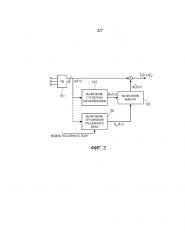
Фиг. 3 показывает схематичную блок-схему предлагаемого изобретения согласно первому примеру для реализации;

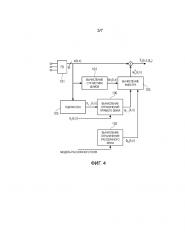
Фиг. 4 показывает схематичную блок-схему предлагаемого изобретения согласно второму примеру для реализации;

Фиг. 5 показывает схематичную блок-схему предлагаемого изобретения согласно третьему примеру для реализации;

Фиг. 6 показывает пример диаграммы направленности захвата, полученной в результате применения методики для извлечения рассеянного звука с использованием фильтра, согласно фиг. 2;

Фиг. 7 показывает пример диаграммы направленности захвата, полученной в результате применения методики для извлечения рассеянного звука с использованием фильтра, согласно фиг. 4; и

Фиг. 8 схематично показывает микрофонный массив и разные звуковые сигналы, которые захвачены микрофонным массивом.

Термины «прямой звук» и «рассеянный звук» определены следующим образом.

Прямой звук: звуки, которые поступают в микрофоны, главным образом, по конкретному выраженному направлению. Прямой звук может представлять собой, например, звук, поступающий прямо от источника звука к микрофону, или отдельное отражение помещения. Прямые звуки могут быть, например, плоскими волнами или сферическими волнами с конкретным направлением поступления. Когда направление поступления прямого звука известно, можно вычислить относительную передаточную функцию прямого звука между микрофонами при условии, что геометрия микрофонов известна.

Рассеянный звук: звук, который поступает в микрофоны со всех направлений. Рассеянный звук может представлять собой, например, позднюю реверберацию, присутствующую в помещении. Обычно, никакие выраженные направления поступления не могут быть связаны с рассеянным звуком (изотропное звуковое поле), т.е. звук поступает с одинаковой средней мощностью со всех направлений. Кроме того, необходимо предположить, что относительные передаточные функции рассеянного звука между микрофонами являются случайными и ненаблюдаемыми. Однако, средние относительные передаточные функции рассеянного звука между микрофонами обычно известны для конкретных расположений микрофонов и моделей рассеянного поля или могут быть измерены.

Нижеследующие подсекции являются кратким изложением существующих методик для извлечения рассеянного звука (или реверберирующего звука) из микрофонной записи. Далее, М означает количество используемых микрофонов. Мы предполагаем, что все микрофонные сигналы были преобразованы в частотно-временную область, где k является индексом частоты, а n является индексом времени (следует отметить, что обычно фильтры могут также применяться во временной области). Микрофоны захватывают L плоских волн (называемых прямым звуком), распространяющихся в рассеянном поле. DOA l-ой плоской волны представлено единичным вектором нормали . В частотно-временной области, сигнал m-го (всенаправленного) микрофона может быть представлен следующим образом:

Здесь, является звуковым давлением l-ой плоской волны, является рассеянным звуком, является стационарным шумом (например, собственным шумом или фоновым шумом), и является вектором, описывающим положение микрофона (m-го микрофона) в данной системе координат.

Целью настоящего изобретения является оценка в положении .

Одноканальные фильтры извлекают рассеянный звук из единственного микрофонного сигнала (). Такие фильтры используются, например, в Направленном звуковом кодировании [Pulkki2007] или в Виртуальном микрофоне [Thiergart2013].

Оценка рассеянного звука определяется путем умножения одного из микрофонных сигналов, например, микрофонного сигнала первого микрофона , на фильтр , например,

Обычно, фильтр является фильтром Винера, который может быть представлен в виде

где является мощностью рассеянного звука, а является мощностью плоских волн и стационарного шума. В некоторых применениях, квадратный корень из фильтра Винера (т.е. квадратный корень из H) используется вместо фильтра Винера. Следует отметить, что для вычисления , необходимо оценить мощность и . Для этой цели, мы можем рассмотреть, например, отношение сигнал-рассеяние (SDR), которое может быть оценено, как объяснено в [Thiergart2012]. В качестве альтернативы, может быть найден посредством оценки, так называемой диффузности, как описано в [Pulkki2007, Thiergart2013]. Оценка SDR или диффузности обычно требует более чем одного микрофона. Тем не менее, рассеянный звук, в конце концов, достигается посредством фильтрации единственного микрофонного сигнала.

Пример системы для извлечения рассеянного звука с использованием одноканального фильтра показан на фиг. 1. Во-первых, SDR (или, альтернативно, диффузность) оценивается на основании множества микрофонных сигналов. Во-вторых, вычисляется фильтр на основании этой информации. Наконец, фильтр умножается на единственный микрофонный сигнал для получения оценки рассеянного звука.

Многоканальные фильтры учитывают микрофонов. Такие фильтры использовались, например, в [Thiergart2013b, Kowalczyk2013]. Для вывода следующих формул, представим M микрофонных сигналов вектором . Рассеянный звук в m-ом микрофоне оценивается через линейную комбинацию M микрофонных сигналов, т.е.

где является комплексным весовым вектором длины M. Веса должны быть вычислены таким образом, чтобы была получена точная оценка рассеянного звука.

Непосредственным способом нахождения подходящего фильтра является вычисление весов таким образом, чтобы L плоских волн были подавлены, при минимизации стационарного шума , который содержится в микрофонных сигналах. В математическом выражении, веса фильтров представляются в виде

,

с учетом линейных ограничений

Здесь, является PSD-матрицей (матрицей спектральной плотности мощности) стационарного шума, т.е. , которая может быть оценена с использованием общеизвестных методик, например, когда отсутствует рассеянный звук и прямой звук. Кроме того, является так называемым вектором распространения. Его элементами являются относительные передаточные функции l-ой плоской волны от m-го микрофона к другим микрофонам. Следовательно, является вектором-столбцом длины M (следует понимать, что только рассеянный звук в m-ом микрофоне оценивается посредством w_m–взвешенной линейной комбинации M микрофонных сигналов; рассеянный звук в других микрофонах является, по существу, излишним, поскольку эти сигналы связаны через относительные передаточные функции от m-го микрофона к другим микрофонам и могут быть вычислены таким образом, при необходимости). Элементы зависят от DOA l-ой плоской волны. Это означает, что является функцией DOA l-ой плоской волны, т.е. . Поскольку зависит от прямого звука (т.е. плоских волн), то далее он упоминается как ограничение прямого звука. С использованием этого пространственного фильтра мы, по существу, создаем формирователь луча, который имеет диаграмму направленности захвата с нулями в направлениях L плоских волн. В результате, все плоские волны подавляются. К сожалению, решение вышеупомянутой задачи минимизации приводит к нулевым весам , поскольку мы имеем только нулевые ограничения, т.е. рассеянный звук не может быть извлечен.

Для преодоления этой проблемы и предотвращения нулевых весов фильтра, [Thiergart2013b, Kowalczyk2013] предлагает использовать тот же фильтр, но с дополнительным ограничением, представленным в виде

где является вектором распространения, который соответствует конкретному DOA , по которому никакие плоские волны не поступают. С использованием этого ограничения, можно предотвратить нулевые веса фильтров, но, все же, нельзя захватить нежелательный прямой звук. В результате, с использованием этого фильтра, захватывается только рассеянный звук и некоторый шум, а все плоские волны затухают. В [Thiergart2013b], DOA , которому соответствует вектор , находится путем выбора направления, которое имеет наибольшее угловое расстояние до всех DOA плоских волн. Например, если единственная плоская волна поступает под углом 0 градусов, то тогда соответствует 180 градусам. К сожалению, DOA не гарантирует, что мы получаем оценку рассеянного звука с настолько малым шумом, насколько это возможно. Кроме того, полученная в результате диаграмма направленности захвата является не очень оптимальной для захвата рассеянного звука, поскольку она становится остронаправленной при более высоких частотах. Это является недостатком, если целью является захват рассеянного звука со всех направлений.

Пример полученной диаграммы направленности захвата показан на фиг. 6. Здесь, два прямых звука поступают с двух азимутальных направлений 51° и 97°. Чертеж показывает полученную диаграмму направленности захвата при частоте 2,8 кГц при использовании однородного линейного массива с 16 микрофонами с интервалами 5 см между микрофонами. Диаграмма направленности захвата имеет нули точно для 51° и 97° и высокий коэффициент усиления для 180°, что соответствует направлению . Кроме того, диаграмма направленности захвата имеет множество других пространственных нулей или низких коэффициентов усиления почти для всех других направлений. Эта диаграмма направленности захвата не подходит для захвата рассеянного звука, который поступает со всех направлений. Следует снова отметить, что ограничения прямого звука прямо связаны с DOA прямых звуков. Необходимая диаграмма направленности захвата, которая не может быть получена с использованием пространственного фильтра в этой подсекции, показана на фиг. 7. Эта диаграмма направленности захвата имеет два пространственных нуля для DOA прямых звуков, а для иных направлений является почти всенаправленной. Эта диаграмма направленности захвата обеспечена с использованием предлагаемого фильтра, который описан ниже со ссылкой на фиг. 7.

Замкнутое по форме решение для вычисления весов фильтра с учетом вышеупомянутых ограничений может быть найдено в [VanTrees2002]. Для вычисления пространственного фильтра, необходимо знать DOA L плоских волн, а именно, вычислить ограничения прямого звука и . Эта DOA-информация может быть определена с использованием общеизвестных узкополосных алгоритмов оценки DOA, таких как Root MUSIC или ESPRIT. Следует дополнительно отметить, что элементы являются обычно комплексными, и обычно должен быть пересчитан для каждого k и n, поскольку следует предположить, что DOA плоских волн являются сильно изменяющимися во времени. Сильная флуктуация может привести к слышимым шумам.

Пример системы для извлечения рассеянного звука с использованием представленного многоканального фильтра показан на фиг. 2. После преобразования микрофонных сигналов в частотно-временную область, мы оцениваем стационарный шум и DOA L плоских волн. Затем, на основании DOA-информации, достигается линейных ограничений прямого звука ( и ). На основе этой информации, могут быть вычислены веса фильтра. Применение этих весов к микрофонным сигналам дает необходимую оценку рассеянного звука. Из этого описания ясно, что полученный фильтр действительно зависит только от прямого звука (т.е. от DOA и соответствующих относительных передаточных функций плоских волн между микрофонами, соответственно), а не от рассеянного звука. Это означает, что фильтр не учитывает потенциально доступную информацию в отношении рассеянного звука, даже если его используют для оценки рассеянного звука.

В настоящем изобретении, мы предлагаем новый многоканальный фильтр для извлечения реверберирующего звука, который преодолевает ограничения вышеупомянутых фильтров. Предлагаемый пространственный фильтр характеризуется диаграммой направленности, которая приближается к всенаправленной диаграмме направленности, за исключением направлений поступления (direction-of-arrival - DOA) прямого звука, для которых она показывает пространственные нули. Это представляет в высшей степени необходимую способность захвата рассеянного звука со всех направлений с низкими искажениями.

Далее, мы предлагаем многоканальный фильтр для оценки рассеянного звука в положении с использованием микрофонов. В отношении многоканальных фильтров, описанных выше, давление рассеянного звука в m-ом микрофоне оценивается посредством выполнения линейной комбинации микрофонных сигналов, т.е.

.

Весовой вектор , который предложен далее, минимизирует конкретную целевую функцию и является линейно ограниченным, подобно многоканальным фильтрам, описанным выше.

Однако, в отличие от многоканальных фильтров, описанных выше, мы предлагаем использовать линейное ограничение, которое не зависит от прямого звука (т.е. от L плоских волн). Точнее, предлагаемое новое ограничение не является функцией DOA плоских волн или соответствующих относительных передаточных функций плоских волн между микрофонами, соответственно.

Напротив, предлагаемое новое ограничение зависит от статистической информации о рассеянном звуке, т.е. предлагаемое новое ограничение зависит от относительных передаточных функций рассеянного звука между микрофонами. Мы покажем далее, что предлагаемое новое ограничение является функцией когерентности или корреляции рассеянного звука между микрофонами. Эта когерентность соответствует средней относительной передаточной функции рассеянного звука между микрофонами.

Предлагаемый пространственный фильтр достигается минимизацией конкретной целевой функции, удовлетворяя ограничение отсутствия искажений для рассеянного звука. Это ограничение соответствует относительной передаточной функции рассеянного звука между микрофонами. В математическом выражении, фильтр вычисляется следующим образом

,

с учетом линейного ограничения

.

Здесь, J является целевой функцией, подлежащей минимизации фильтром. Целевая функция может быть, например, мощностью стационарного шума на выходе фильтра, энергией помехи на выходе фильтра, или квадратичной ошибкой оцененного рассеянного звука. Примеры для J будут обеспечены в вариантах осуществления. Вектор ограничения можно представить в виде . m'-ый элемент является относительной передаточной функцией рассеянного звука между микрофонами m и m'. Эту относительную передаточную функцию можно представить в виде

.

Следует отметить, что m-ый элемент равен 1. С использованием этого ограничения, мы захватываем рассеянный звук без искажений. Фактически, пусть является вектором, содержащим записанный рассеянный звук. С использованием уравнений, приведенных выше, этот вектор может быть записан в следующем виде

.

Рассеянный звук на выходе фильтра можно представить в виде выражения , которое идентично , поскольку . Таким образом, этот фильтр захватывает рассеянный звук без искажений. Относительные передаточные функции в обычно не могут быть оценены на практике, поскольку они являются, по существу, случайными, т.е. мы имеем разную реализацию передаточной функции для каждого k и n. Таким образом, вычисляется как средняя относительная передаточная функция между микрофонами m и m', т.е.

.

Эта средняя относительная передаточная функция соответствует так называемой пространственной когерентности рассеянного звука между микрофонами m и m', которая определяется в качестве

,

где (.)* означает комплексно сопряженную величину. Эта пространственная когерентность описывает корреляцию рассеянного звука между микрофонами m и m' в частотной области. Эта когерентность зависит от конкретного рассеянного звукового поля. Когерентность может быть измерена заранее для данного помещения. Альтернативно, когерентность известна из теории конкретных рассеянных звуковых полей [Elko2001]. Например, для сферически изотропного рассеянного звукового поля, которое часто рассматривается на практике, мы имеем

,

где sinc означает sinc-функцию, f является акустической частотой для данного частотного диапазона k, и c является скоростью звука. Кроме того, является расстоянием между микрофонами m и m'. При использовании пространственной когерентности в качестве линейного ограничения , которое представляет среднюю относительную передаточную функцию рассеянного звука между микрофонами, полученный фильтр является эквивалентным сумме многих линейно ограниченных пространственных фильтров, причем каждый из этих фильтров захватывает разную реализацию случайного рассеянного звука без искажений.

С использованием ограничения рассеянного звука, введенного выше, мы получаем пространственный фильтр, который захватывает рассеянный звук одинаково хорошо со всех направлений. Это является отличием от многоканальных фильтров, описанных выше, которые захватывают звук, главным образом, по одному направлению, а именно, по направлению, которому соответствует выбранный вектор распространения .

Следует отметить, что ограничение рассеянного звука , концептуально, сильно отличается от ограничений прямого звука и . Таким образом, новый фильтр, предложенный в этом разделе, является, концептуально, сильно отличающимся от многоканальных фильтров, описанных выше.

Блок-схема предложенного изобретения показана на фиг. 3. Во-первых, M микрофонные сигналы преобразуются в частотно-временную область (или другую подходящую область для обработки сигналов) с использованием банка (101) фильтров (filterbank - FB). Во-вторых, мы вычисляем вектор линейного ограничения рассеянного звука в блоке (102). Вектор ограничения рассеянного звука оценивается либо на основании сигнала, либо он соответствует, например, теоретической пространственной когерентности для конкретного предлагаемого рассеянного поля, как упомянуто выше. В блоке (104), мы оцениваем конкретную статистику (например, статистику шумов) на основании микрофонных сигналов. Эта информация, которая обычно представляется в виде PSD-матрицы , используется для генерации целевой функции J, которая должна быть минимизирована фильтром. Веса фильтра, который минимизирует целевую функцию с учетом ограничения рассеянного звука, вычисляются в блоке (103). Наконец, веса применяются к микрофонным сигналам, что обеспечивает в результате необходимую оценку рассеянного звука. Конкретные реализации настоящего изобретения представлены в нижеследующих вариантах осуществления.

МИНИМИЗАЦИЯ ВЫХОДНОЙ МОЩНОСТИ, УДОВЛЕТВОРЯЮЩЕЙ ОГРАНИЧЕНИЮ РАССЕЯННОГО ЗВУКА

В этом варианте осуществления, мы определяем пространственный фильтр, который минимизирует всю выходную мощность фильтра с учетом ограничения рассеянного звука. Ограничение рассеянного звука обеспечивает, то что рассеянный звук сохраняется пространственным фильтром, в то время как остальные части сигнала (нежелательный стационарный шум и плоские волны) минимизируются. Веса фильтра вычисляются следующим образом:

,

с учетом линейного ограничения

.

Замкнутое по форме решение для этого фильтра приведено в [VanTrees2002] в виде

.

Здесь, является PSD-матрицей микрофонных сигналов, которая может быть вычислена следующим образом:

,

где является вектором, содержащим микрофонные сигналы. На практике, математическое ожидание аппроксимируется, например, путем временного усреднения. Кроме того, элементы вектора ограничения соответствуют пространственной когерентности рассеянного звука между микрофонами m и m', т.е.

.

Фактически, пространственная когерентность не должна зависеть от времени (а именно, ), следовательно, пространственная когерентность может быть оценена заранее или может предполагать теоретическое значение. Пространственная когерентность может быть оценена либо на основании микрофонных сигналов (во время периодов, когда присутствует только рассеянный звук) с использованием

,

либо может быть представлена в виде априорной информации, предполагающей конкретное рассеянное звуковое поле. В последнем случае, мы используем, например, пространственную когерентность для сферически изотропного рассеянного звукового поля, т.е.

.

Следует отметить, что sinc-функция может быть заменена другими функциями, в зависимости от предполагаемого звукового поля. Для разных рассеянных звуковых полей существуют разные функции когерентности, которые априори известны. Примеры могут быть найдены в [Elko2001].

Блок-схема этого варианта осуществления показана на фиг. 3. После преобразования микрофонных сигналов с использованием банка (101) фильтров, мы вычисляем сигнальную PSD-матрицу в блоке (104) оценки статистики сигналов. Кроме того, мы вычисляем вектор линейного ограничения рассеянного звука в блоке (102), либо на основании сигнала, либо с использованием априорной информации, предполагающей конкретное рассеянное звуковое поле. Веса фильтра, затем, вычисляются в блоке (103). Умножение весов на микрофонные сигналы дает необходимую оценку рассеянного звука.

Фильтр, вычисленный в этом варианте осуществления, имеет следующие преимущества по сравнению с другим пространственным фильтром (например, фильтрами, описанными в предшествующем уровне техники):

- Поскольку мы минимизируем весь выходной сигнал, фильтр обеспечивает оптимальное соотношение между затуханием L плоских волн и стационарным шумом.

- Необходимую сигнальную PSD-матрицу , и, таким образом, фильтр, легко вычислить на практике.

- Не требуется никакой информации о DOA L плоских волн.

ЛИНЕЙНО ОГРАНИЧЕННЫЙ ФИЛЬТР С МИНИМАЛЬНОЙ ДИСПЕРСИЕЙ

Этот вариант осуществления представляет собой комбинацию новой методики и методики предшествующего уровня техники в отношении многоканальных фильтров, описанных выше в соответствии с фиг. 2. В этом варианте осуществления, мы определяем линейно ограниченный пространственный фильтр, который минимизирует стационарный шум на выходе фильтра, с учетом рассеянного ограничения и дополнительных направленных ограничений. Веса фильтра вычисляются в виде

,

с учетом линейных ограничений

и

Ясно, что фильтр минимизирует только стационарный шум на выходе. Нежелательные плоские волны подавляются с использованием вторых линейных ограничений (как объяснено выше для многоканальных фильтров, фиг. 2). Эти дополнительные ограничения, по сравнению с фильтром, минимизирующим выходную мощность, в соответствии с фиг. 3, обеспечивают еще более сильное подавление создающих помехи плоских волн. Полученный в результате фильтр, тем не менее, сохраняет рассеянный звук благодаря первому линейному ограничению. Замкнутое по форме решение для этого фильтра, которое может быть вычислено на практике, может быть представлено в виде

Здесь, вектор является матрицей ограничений, содержащей линейные ограничения, определенные выше, и (O является нулевым вектором длины L) являются соответствующими характеристиками. В отнош